Лабораторная работа 5 Оценка работы систем массового обслуживания с отказами Задача 1
 Скачать 41 Kb.
|
|
Лабораторная работа №5 Оценка работы систем массового обслуживания с отказами Задача 1. Рассматривается круглосуточная работа пункта проведения профилактического осмотра машин с одним каналом (одной группой проведения осмотра). На осмотр и выявление дефектов каждой машины затрачивается в среднем 0,5 часа. На осмотр поступает в среднем 36 машин в сутки. Потоки заявок и обслуживания – простейшие. Если машина, прибывшая в пункт осмотра, не застает ни одного канала свободным, она покидает пункт осмотра необслуженной. Определить вероятности состояний и характеристики обслуживания профилактического пункта осмотра. Задания к задаче 1: 1. Ввести исходные данные. 2. Рассчитать по формулам Эрланга вероятности состояний 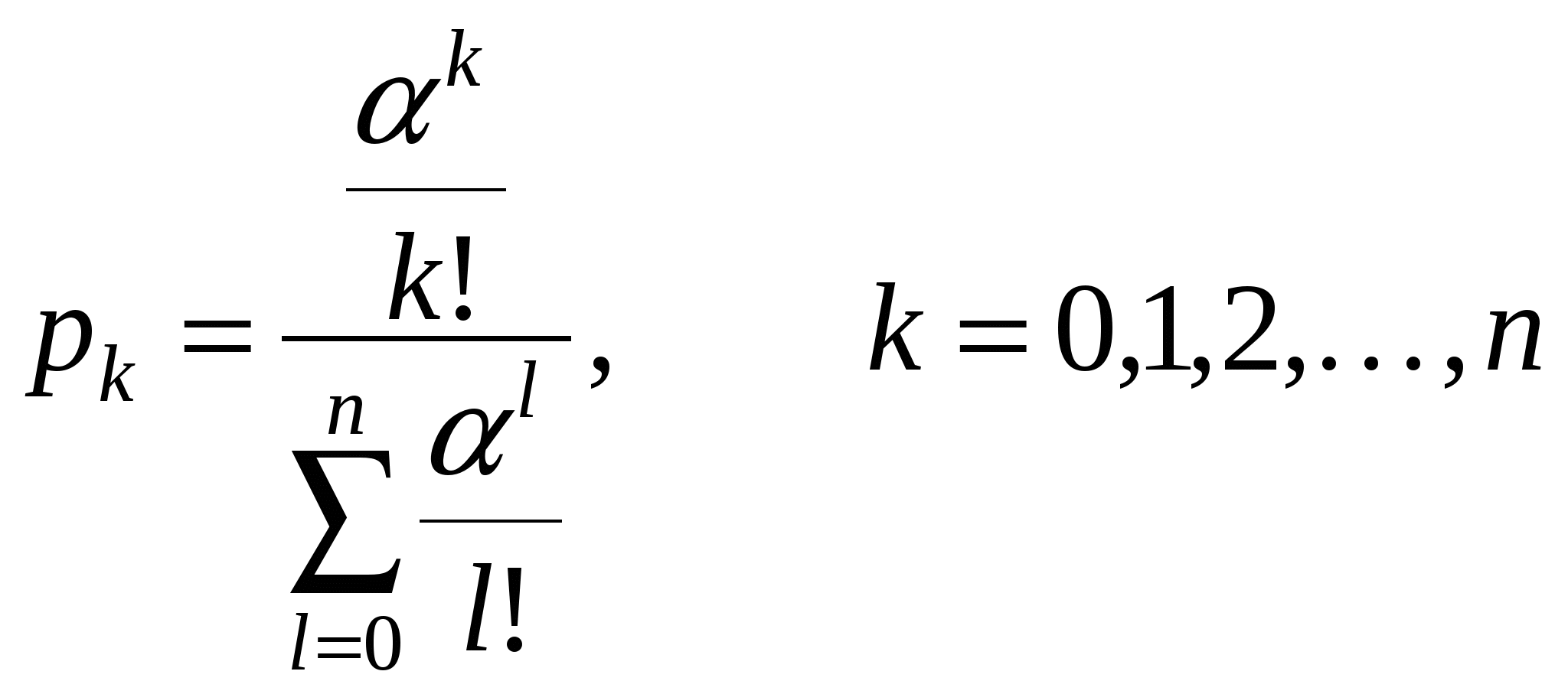 .3. Определить абсолютную пропускную способность:  .4. Оценить коэффициент загрузки пункта:  .5. Сделать выводы об эффективности работы пункта проведения профилактического осмотра машин. Задача 2. Пункт по ремонту радиотехники работает в режиме отказа с одним мастером. Интенсивность потока заявок λ, производительность мастера μ. Определить предельные значения относительной пропускной способности Q, абсолютной пропускной способности А и вероятность отказа Ротк телефонной линии. Определить также среднее время обслуживания одного вызова, среднее время простоя канала и вероятность того, что канал свободен или занят. Задача 3. Статистическими исследованиями в результате наблюдения установлено, что интенсивность потока телефонных звонков коммерческому директору λ = 1.2 вызова в минуту, средняя продолжительность разговора (обслуживания заявки) tобсл = 2.5 мин и все потоки событий (вызовов и обслуживания) имеют характер простейших пуассоновских потоков. Определим предельную (относительную и абсолютную) пропускную способность СМО, вероятность отказа, а также полное число обслуженных и необслуженных (получивших отказ) заявок в течение 1 ч работы СМО. Сравнить фактическую пропускную способность СМО с номинальной, т.е. с пропускной, способностью, которой обладала бы система в том случае, если бы каждая заявка обслуживалась ровно 2,5 мин и все заявки следовали бы одна за другой без перерыва. Задача 4. В вычислительный центр коллективного пользования с тремя ЭВМ поступают заказы от предприятий на вычислительные работы. Если работают все три ЭВМ, то вновь поступающий заказ не принимается, и предприятие вынуждено обратиться в другой вычислительный центр. Среднее время работы с одним заказом составляет 3 часа. Интенсивность потока заявок 0,25 заявок/час. Найти предельные вероятности состояний и показатели эффективности работы вычислительного центра. Задания к задаче 4: 1. Рассчитать по формулам Эрланга вероятности состояний. 2. Определить абсолютную пропускную способность вычислительного центра. 3. Оценить среднее число занятых ЭВМ:  .4. Оценить коэффициент загрузки вычислительного центра  .5. Сделать выводы об эффективности работы вычислительного центра. Задача 5. Решить задачу 1 для случая  канала (групп проведения осмотра). Найти число каналов, при котором относительная пропускная способность пункта будет не менее 0,9.Задания к задаче 5: 1. Рассчитать по формулам Эрланга вероятности состояний. 2. Определить абсолютную пропускную способность пункта проведения профилактического осмотра машин. 3. Оценить среднее число занятых групп. 4. Оценить коэффициент загрузки пункта проведения профилактического осмотра машин. 5. Варьируя количеством групп проведения осмотра (  ), найти такое количество каналов, при котором относительная пропускная способность пункта ( ) будет не менее 0,9.6. Сделать выводы об эффективности работы пункта проведения профилактического осмотра машин. Задача 6. Коммерческая фирма занимается посреднической деятельностью по продаже автомобилей и осуществляет часть переговоров по 3 телефонным линиям. В среднем поступает 75 звонков в час. Среднее время предварительных переговоров справочного характера составляет 2 мин. Задача 7. Пункт по ремонту квартир работает в режиме отказа и состоит из двух бригад. Интенсивность потока заявок λ, производительность пункта μ. Определить вероятность того, что оба каналы свободны, один канал занят, оба канала заняты, вероятность отказа, относительную и абсолютную пропускные способности, средне число занятых бригад. |