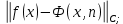лаба. Лабораторная работа 5 По математическому анализу разложение функций в тригонометрический ряд фурье
 Скачать 145.22 Kb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего образования «Казанский национальный исследовательский технический университет им. А.Н. Туполева-КАИ» (КНИТУ-КАИ) Институт компьютерных технологий и защиты информации Кафедра прикладной математики и информатики Лабораторная работа №5 По МАТЕМАТИЧЕСКОМУ АНАЛИЗУ РАЗЛОЖЕНИЕ ФУНКЦИЙ В ТРИГОНОМЕТРИЧЕСКИЙ РЯД ФУРЬЕ Вариант №7 Выполнил : студент группы 4110, Курбангалеев Айдар Ильдарович, Номер зачетной книжки 041397
Казань 2021 Лабораторная работа №5 РАЗЛОЖЕНИЕ ФУНКЦИИ В ТРИГОНОМЕТРИЧЕСКИЙ РЯД ФУРЬЕ. Цель работы: научится разлагать произвольные функции в тригонометрический ряд Фурье с помощью пакетов компьютерной математики. 1. Проверка условия Дирихле Данная функция не является периодической. Но учитывая, что в нашей задаче входит разложение функции только на отрезке  мы можем раскладывать в ряд Фурье другую функцию  Где  вычисляет целую часть аргумента по обычным арифметическим правилам. Новая функция f1(x) является 2L- периодической, полностью удовлетворяет условиям Дирихле и, кроме того, равна исходной функции на исследуемой области  . Данная функция является четной. Но для общности решения задачи Фурье мы не будем учитывать свойство четности данной функции и разложим еѐ по общим формулам.2. Построение графика функции Введем функцию 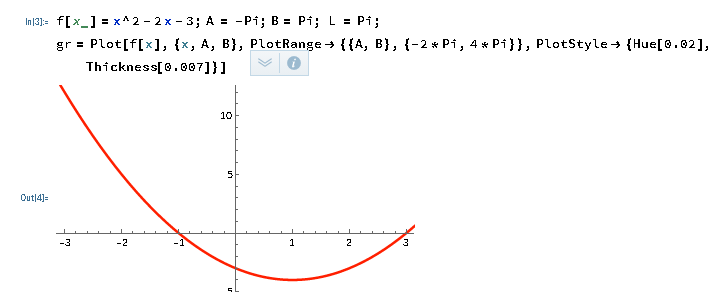 ,  отрезок и L= π . И построим график этой функции. 3. Построение тригонометрического ряда Фурье Вводим функции, значения которых есть коэффициенты n -го члена ряда Фурье  Введём функцию Ф (x, K) приближенно в виде суммы первых K членов тригонометрического ряда Фурье: 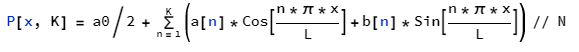 Построим график частичной суммы Ф (x, K при K 1: 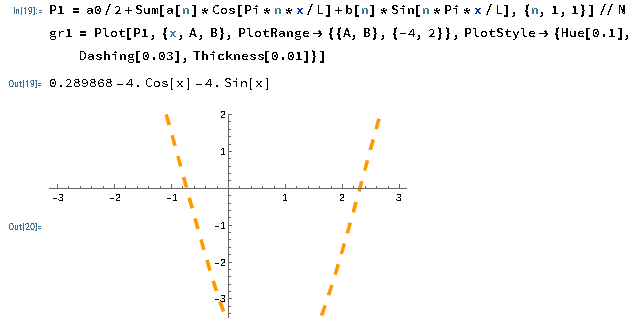 Построим график частичной суммы Ф (x, K при K 2: 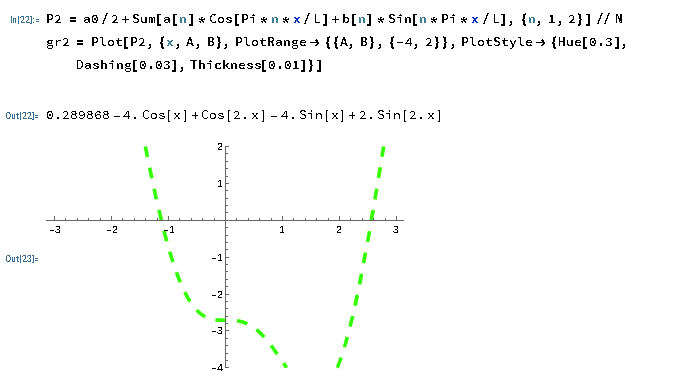 Построим график частичной суммы Ф (x, K при K 30: 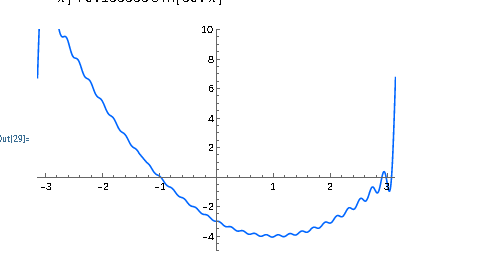  Совместим графики Ф (x, 1, Ф (x, 2 и Ф (x, 35 для определения сходимости к f(x): 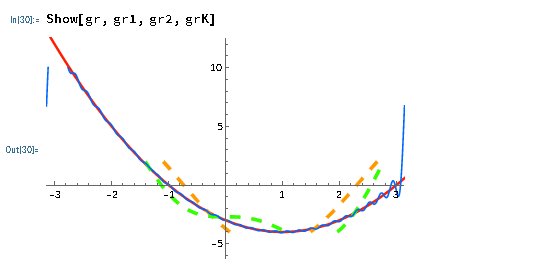 Приведем пример программы в Wolfram Mathematica разложения функции f(x) в тригонометрический ряд Фурье: 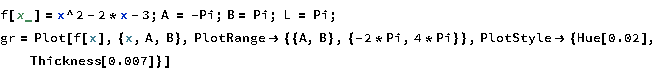 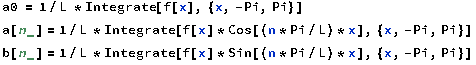 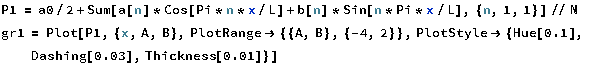 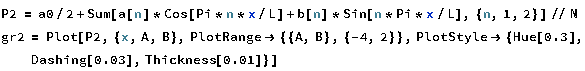 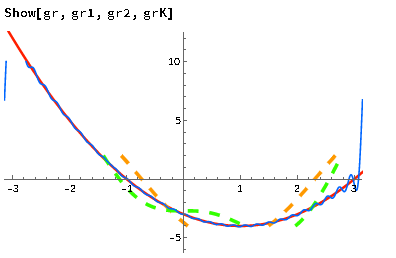  Оценка качества аппроксимации Разложение заданной функции в тригонометрический ряд Фурье достаточно быстро сходится к периодической функци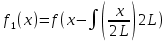и  , где Int(x) – функция, округляющая аргумент по стандартным правилам округления, принятым в математике. K указывает сколько слагаемых в разложении ряда Фурье необходимо учитывать. На рисунке видно, что при K 30 график частичной суммы Ф (x, 30 и функции f(x) почти совпадают. Чтобы оценить качество равномерной аппроксимации функции f(x) на промежутке ; , надо вычислить расстояние в метрике ; : 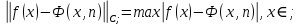  Оценка качества аппроксимации
Вывод В этой лабораторной работе мы научились раскладывать произвольную функцию в тригонометрический ряд Фурье. Оценив точность, получаем, что разложение при K = 30 достаточно близко сходится к данной функции |
