ИИ ЛР №5. Лабораторная работа 5 создание однонаправленной многослойной нейронной сети по дисциплине Введение в системы искусственного интеллекта

• Название: Лабораторная работа 5 создание однонаправленной многослойной нейронной сети по дисциплине Введение в системы искусственного интеллекта
• Дата: 23.12.2021
• Размер: 65.99 Kb.
• Имя файла: ИИ ЛР №5.docx
• Тип: Лабораторная работа; #316236

МИНОБРНАУКИ РОССИИ

Федеральное государственное бюджетное

образовательное учреждение высшего образования

«Тульский государственный университет»
Институт прикладной математики и компьютерных наук

Кафедра «Вычислительная техника»
Лабораторная работа №5

«СОЗДАНИЕ ОДНОНАПРАВЛЕННОЙ МНОГОСЛОЙНОЙ НЕЙРОННОЙ СЕТИ»

по дисциплине

«Введение в системы искусственного интеллекта»

Выполнил студент гр. 220681:

Северин Д. В.

Проверил:

к.т.н. доц. Семенчев Е.А.

Тула 2021 г.

1. Цель работы

Цель занятия – освоение основных этапов реализации нейронно-сетевого подхода при построении многослойной нейронной сети, обучающейся с учителем.

2. Задание

2.1. Изучить общие принципы построения многослойных иерархических сетей.

2.2. Изучить алгоритм обучения с учителем для многослойного персептрона, основанный на методе обратного распространения ошибки.

3. Ход работы

Функция нейрона состоит в вычислении взвешенной суммы его входов с дальнейшим нелинейным преобразованием ее в выходной сигнал: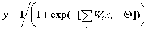



Выходы нейронов выходного слоя описывают результат классификации Y=Y(X). Особенности работы персептрона состоят в следующем:

- каждый нейрон суммирует поступающие к нему сигналы от нейронов предыдущего уровня иерархии с весами, определяемыми состояниями синапсов, и формирует ответный сигнал (переходит в возбужденное состояние), если полученная сумма выше порогового значения.

- персептрон переводит входной образ, определяющий степени возбуждения нейронов самого нижнего уровня иерахии, в выходной образ, определяемый нейронами самого верхнего уровня. Число последних, обычно, сравнительно невелико. Состояние возбуждения нейрона на верхнем уровне говорит о принадлежности входного образа к той или иной категории.

- допустимые состояния синаптических связей определяются произвольными действительными числами, а степени активности нейронов - действительными числами между 0 и 1.

Нейросеть, тренируемая через обратное распространение, пытается использовать входные данные для предсказания выходных.

Предположим, нам нужно предсказать, как будет выглядеть колонка «выход» на основе входных данных. Обратное распространение, в самом простом случае, рассчитывает подобную статистику для создания модели.

Код программы представлен в приложении.

Основные параметры модели представлены в Таблице 1.

• 
  X: матрица входного набор данных
  
• 
  y: матрица выходного набора данных
  
• 
  l₀: первый слой сети, определённый входными данными
  
• 
  l₁: второй слой сети, или скрытый слой
  
• 
  Syn0: первый слой весов, Synapse 0, объединяет l0 с l1
  
• 
  *: поэлементное умножение – два вектора одного размера умножают соответствующие значения, и на выходе получается вектор такого же размера
  
• 
  -: поэлементное умножение – два вектора одного размера умножают соответствующие значения, и на выходе получается вектор такого же размера
  
• 
  x.dot(y): если x и y – это вектора, то на выходе получится скалярное произведение. Если это матрицы, то получится перемножение матриц. Если матрица только одна из них – это перемножение вектора и матрицы.
  

Импортируем библиотеку линейной алгебры:

import numpy as n

Далее создаем функцию «сигмоиду». Она ставит в соответствие любое число значению от 0 до 1 и преобразовывает числа в вероятности, а также имеет несколько других полезных для тренировки нейросетей свойств:

def nonlin(x,deriv=False):

Инициализация массива входных данных в виде numpy-матрицы. Каждая строка – тренировочный пример. Столбцы – это входные узлы. У нас получается 3 входных узла в сети и 4 тренировочных примера:

X = np.array([ [0,0,1], …

Инициализирует выходные данные. ".T" – функция переноса. После переноса у матрицы y есть 4 строки с одним столбцом. Как и в случае входных данных, каждая строка – это тренировочный пример, и каждый столбец (в нашем случае один) – выходной узел. У сети, получается, 3 входа и 1 выход:

y = np.array([[0,0,1,1]]).T

Матрица весов сети syn0. Её размерность (3, 1), поскольку у нас есть 3 входа и 1 выход. Иными словами, l₀ имеет размер 3, а l₁ – 1. Поскольку мы связываем все узлы в l₀ со всеми узлами l₁, нам требуется матрица размерности (3, 1):

syn0 = 2*np.random.random((3,1)) – 1

Цикл с кодом тренировки сети повторяется многократно и оптимизирует сеть для набора данных:

for iter in range(10000):

Первый слой, l₀, это просто данные. В X содержится 4 тренировочных примера. Мы обработаем их все и сразу – это называется групповой тренировкой [full batch]. Итого мы имеем 4 разных строки l₀, но их можно представить себе как один тренировочный пример – на этом этапе это не имеет значения (можно было загрузить их 1000 или 10000 без всяких изменений в коде):

l0 = X

Это шаг предсказания. Мы позволяем сети попробовать предсказать вывод на основе ввода. Затем мы посмотрим, как это у неё получается, чтобы можно было подправить её в сторону улучшения.

l1 = nonlin(np.dot(l0,syn0))

В строке содержится два шага. Первый делает матричное перемножение l₀ и syn0. Второй передаёт вывод через сигмоиду. Размерности у них следующие:

(4 x 3) dot (3 x 1) = (4 x 1)

Матричные умножения требуют, чтобы в середине уравнения размерности совпадали. Итоговая матрица имеет количество строк, как у первой, а столбцов – как у второй. Мы загрузили 4 тренировочных примера, и получили 4 догадки (матрица 4х1). Каждый вывод соответствует догадке сети для данного ввода:

l1_error = y - l1

Поскольку в l₁ содержатся догадки, мы можем сравнить их разницу с реальностью, вычитая её l₁ из правильного ответа y. l₁_error – вектор из положительных и отрицательных чисел, характеризующий «промах» сети.

l1_delta = l1_error * nonlin(l1,True)
Первая часть: производная

nonlin(l1,True)

Полное выражение: производная, взвешенная по ошибкам:

l1_delta = l1_error * nonlin(l1,True)

Умножая производные на ошибки, мы уменьшаем ошибки предсказаний, сделанных с высокой уверенностью. Если догадка в сети близка к нулю (х=0, у=0,5), то она не особенно уверенная. Мы обновляем эти неуверенные предсказания и оставляем в покое предсказания с высокой уверенностью, умножая их на величины, близкие к нулю:

syn0 += np.dot(l0.T,l1_delta)

Результат работы программы представлен на рисунке 3.



Рисунок 3 – Результат тестирования программы

4. Вывод

В результате работы была создана многослойная иерархическая сеть и был реализован алгоритм обучения с учителем для многослойного персептрона, основанный на методе обратного распространения ошибки.

ПРИЛОЖЕНИЕ

Листинг файла main.py

import numpy as np
# Сигмоида
def nonlin(x, deriv=False):
if (deriv == True):
return x * (1 - x)
return 1 / (1 + np.exp(-x))


# набор входных данных
X = np.array([[0, 0, 1],
[0, 1, 1],
[1, 0, 1],
[1, 1, 1]])

# выходные данные
y = np.array([[0, 0, 1, 1]]).T

# сделаем случайные числа более определёнными
np.random.seed(1)

# инициализируем веса случайным образом со средним 0
syn0 = 2 * np.random.random((3, 1)) - 1

for iter in range(10000):
# прямое распространение
l0 = X
l1 = nonlin(np.dot(l0, syn0))


# насколько мы ошиблись?
l1_error = y - l1

# перемножим это с наклоном сигмоиды
# на основе значений в l1
l1_delta = l1_error * nonlin(l1, True) # !!!

# обновим веса
syn0 += np.dot(l0.T, l1_delta) # !!!

print("Выходные данные после тренировки:")
print(l1)