Нейронные сети. Задача обучения с учителем научиться предсказывать у. Структура обучения с учителем х Алгоритм У

• Название: Задача обучения с учителем научиться предсказывать у. Структура обучения с учителем х Алгоритм У
• Дата: 25.03.2023
• Размер: 3.9 Mb.
• Имя файла: Нейронные сети.docx
• Тип: Задача; #1014546

Нейронные сети

Введение в нейронные сети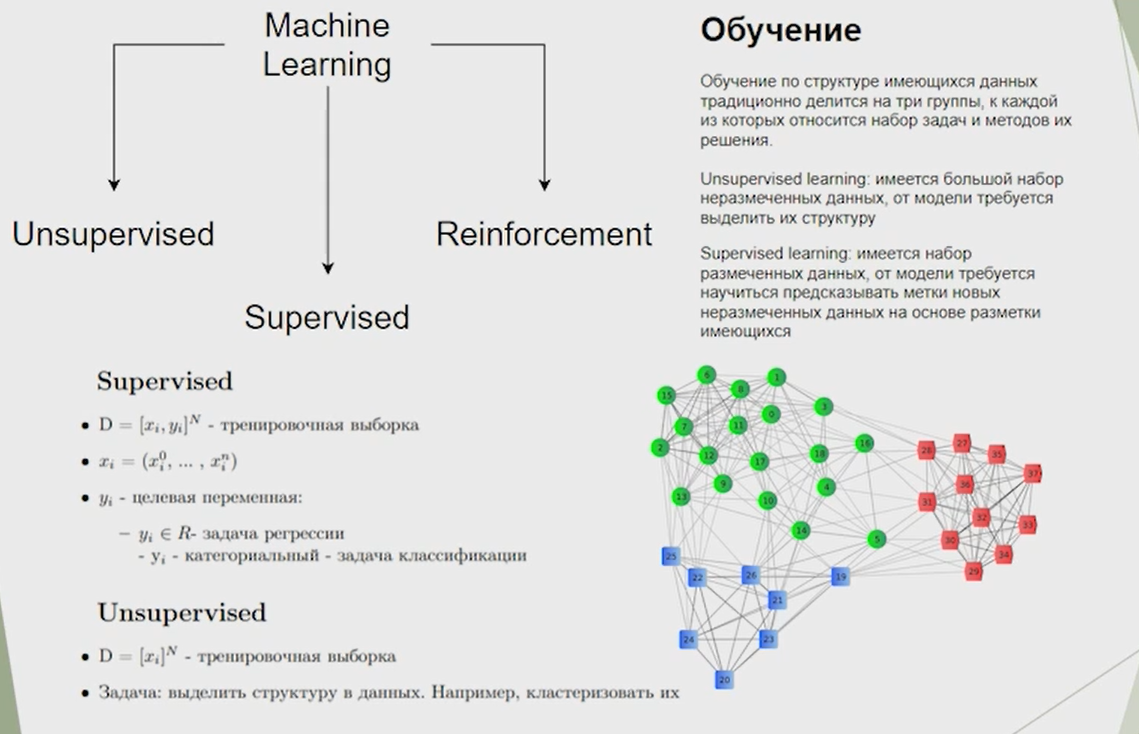



Когда мы говорим о машинном обучении, рассматриваем 3 сущности:

1. 
   Входные данные, которые нам предлагаются
   
2. 
   Далее применяем к ним некоторый алгоритм
   
3. 
   И получаем некоторый ответ
   

Вопрос в том, какой формат имеют входные и выходные данные?

Supervised learning (обучение с учителем)

Входные данные поступают парами {(x, y},

где х – признаковое описание объекта

у – ответ на некоторый вопрос, который мы задаем (метки)

Задача обучения с учителем – научиться предсказывать у.

Структура обучения с учителем:

Х  Алгоритм  У

Какие задачи встают? Зависит от формата метки у.

1. 
   Классификация:
   

Когда у имеет бинарный ответ: да или нет, 0 и 1, -1 и 1

Многоклассовая классификация {1…N}, например:

Есть темы: спорт, наука, политика, рыбалка (у). Когда имеем на входе текст (х), нужно придумать алгоритм, чтобы вышла одна из меток.

2. 
   Восстановление регрессии (регрессия)
   

У может принимать любые значения из какого-то интервала.

Это значит, что мы пытаемся предсказать некоторую непрерывную величину (котировка акций, рост человека)

3. 
   Ранжирование
   

Пытаемся упорядочить некоторое множество, которое было дано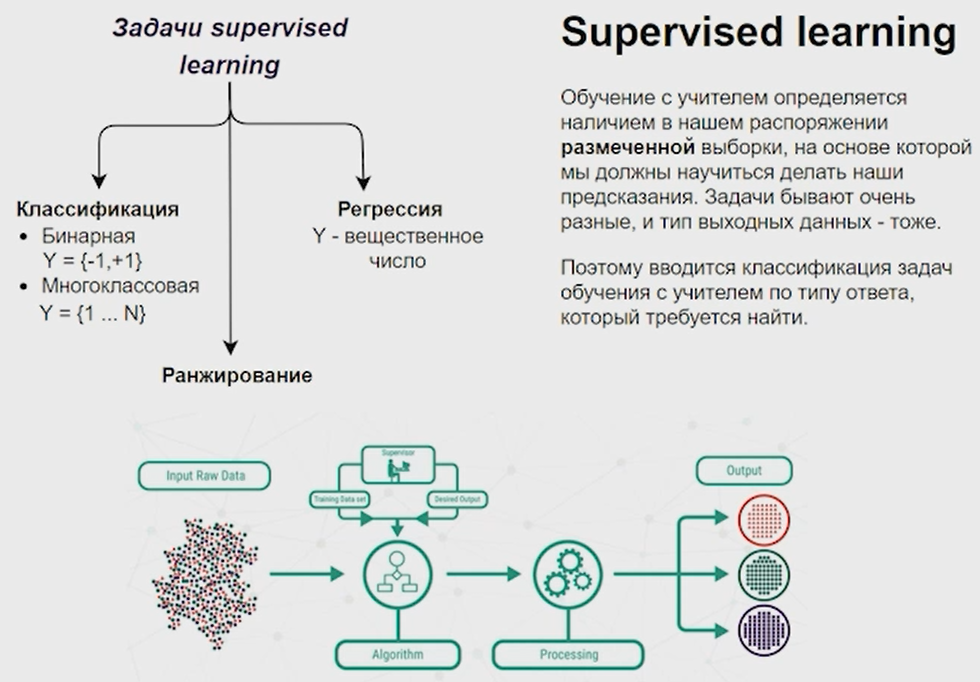



UNSupervised learning (обучение без учителя)

Пытаемся не предсказывать метки, а структуризировать ту информацию, которая нам уже дана.

На входе даются только х, а на выходе ожидаем описание некоторой структуры, которую мы обнаружили в этих данных.

Задачи:

1. 
   Кластеризация
   

Пытаемся обнаружить внутри нашего признакового описания объектов (пространства иксом) некоторые кластеры

Например, на графике можно выделить три кластера: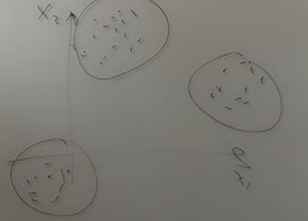



Задача – научить выделять модель кластерные структуры внутри данных, она не пытается предсказать заранее.

2. 
   Задача понижения размерности с потерей наименьшего количества информации
   
3. 
   Выделение последовательностей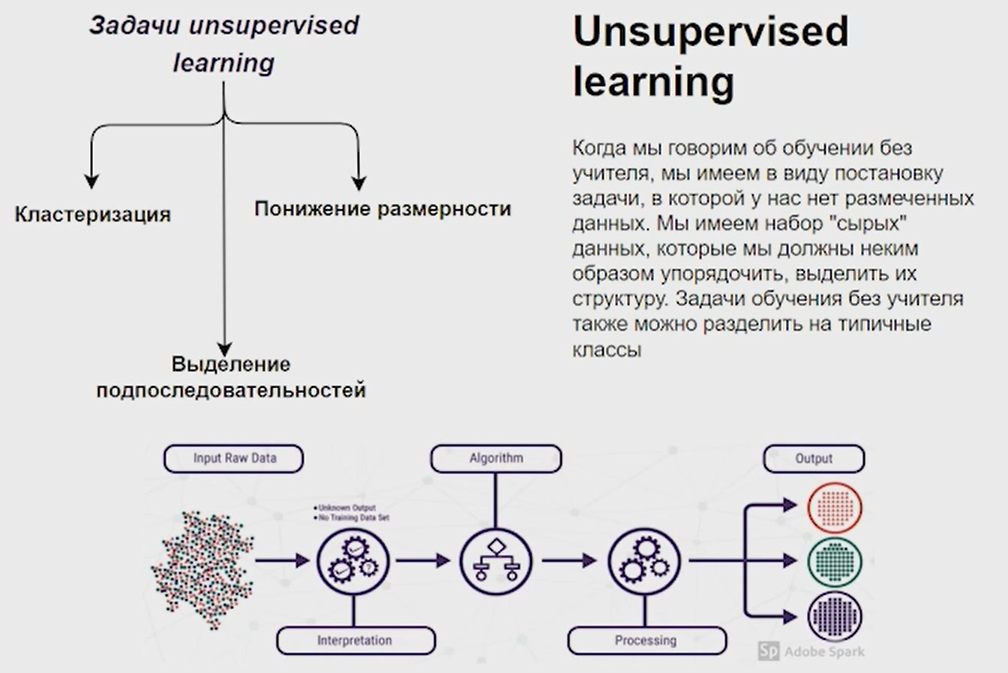
   

Предсказательная модель

Функции, которые друг на друга сильно похожи. Отличаются лишь значением параметров. Чем больше емкость, тем лучше.



Графы вычислений – возможность представить некоторую функцию в виде некоторого графа.

Например: есть функция, на вход подаем два аргумента a, b.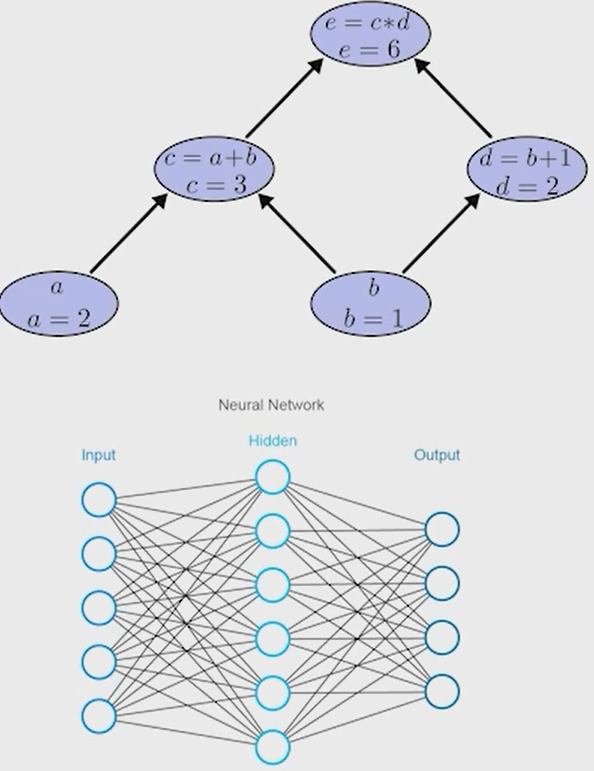



Интуитивное представление о нейронных сетях

Интуиция:

(дополнить из конспекта на работе)

Полносвязные нейронные сети

(NN. FeedForward)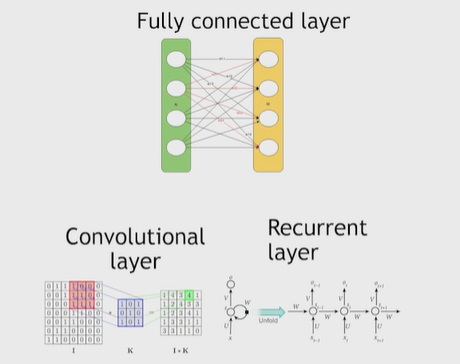



Суть – пытаемся объединить низкоуровневые признаки в высокоуровневые признаки.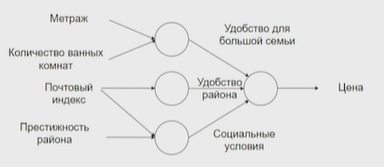



Еще об интуиции:

Биологический нейрон работает как накопитель заряда, приобретая свойство проводимости лишь тогда, когда будет накоплен определенный заряд.

Перцептрон Розенблатта, Пороговая функция (функция Хевисайда, функция активации)



Нейрон – блок логистической регрессии с некоторой функцией активации. Вектор признаков подается по отдельности на каждый из нейронов слоя, каждый нейрон производит с ним свое собственное линейное преобразование, передавая полученный результат на следующий слой и так далее. Таким образом, полученную структуру можно математически описать последовательным перемножением матриц и применении функции активации в каждом слое. Нейрон содержит в себе вектор весов и функцию активации.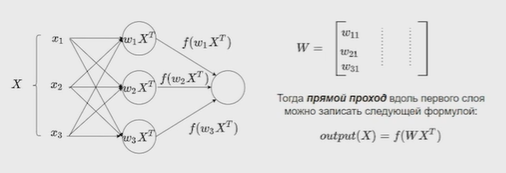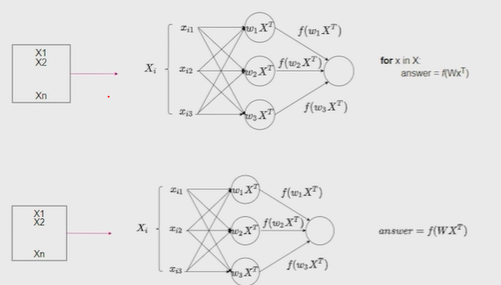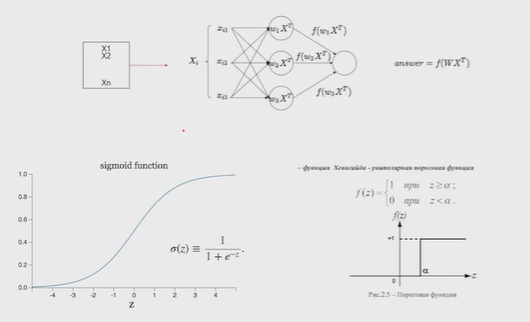







Обучение делится на 3 этапа:

1. 
   Выбор параметрического семейства функций, которое мы называем моделью. Выбираем нейронную сеть и архитектуру.
   
2. 
   Оценить, чем одна нейронная сеть лучше, чем другая. То есть, придумать способ их сравнения.
   
3. 
   Подобрать с точки зрения сравнения нейронных сетей наилучшую.
   

Capacity – то, насколько модель может быть выразительной, емкой, насколько большие закономерности она может выучить, обобщить.

Как описать математически? Чем больше параметров, тем больше данных может обобщить.



Как отследить переобучение модели?

При помощи построения графика зависимости качества на тестовых выборках (на трейне растет, а на тестовой падает)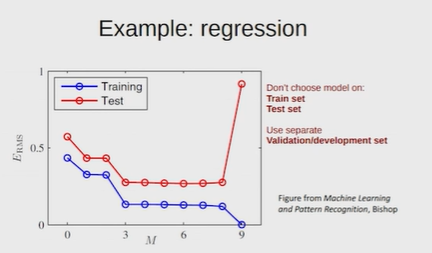



Лучший способ бороться с переобучением – взять больше данных.

Зачем нужны функции активации?

Если не будем их применять, то тогда нелинейное преобразование заменится на линейное, все слои будут преобразованы в одно линейное.

У функции активации есть свойства: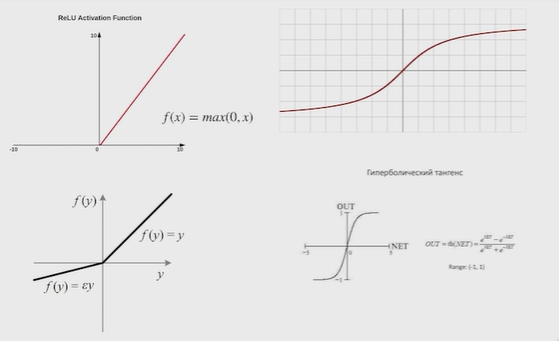



Это нужно в задачах классификации.

Гиперболический тангенс – функция активации, принимает значения от -1 до 1, при стремлении бесконечности х растет до 1, при стремлении к минус бесконечности, убывает, но не до 0, а до -1. Используется часто в задачах классификации.1000 предсказать не может.

Функция гиперболического тангенса: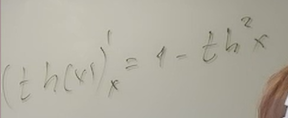



Производная гиперболического тангенса: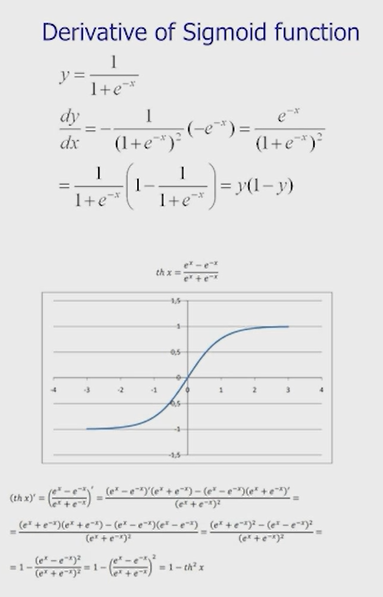



Практикум для самостоятельной работы (с ответами)

Задачи:

1. 
   Основная особенность нейрона, позволяющая использовать его для анализа чего-либо?
   
2. 
   Что такое перцептрон Розенблатта?
   
3. 
   Какую же структуру вообще можно назвать нейроном?
   
4. 
   Опишите этапы машинного обучения в контексте нейронных сетей.
   
5. 
   Повторите функцию гиперболического тангенса.
   

 

Процесс выполнения:

1. 
   Имеется ввиду его способность накапливать определённый электрический заряд, и пропускать его при достижении строго определённого значения. Эта особенность находит применение при работе с анализом данных.
   
2. 
   Это - математическая или компьютерная модель восприятия информации мозгом ( кибернетическая модель мозга ), предложенная Фрэнком Розенблаттом в 1958 году и впервые реализованная в виде электронной машины «Марк-1» в 1960 году. Перцептрон стал одной из первых моделей нейросетей, а «Марк-1» — первым в мире нейрокомпьютером.
   
3. 
   Это некий алгоритм, на вход которого подаётся информационная матрица. Алгоритм содержит в себе набор весов, которые, перемножившись на элементы матрицы, дают набор обработанных по определённым параметрам данных.
   
4. 
   Первый этап - это, собственно, выбор обучающей модели (в нашем случае - это нейронная сеть), второй этап - это оценка ряда нейросетей по определённым параметрам, и третий этап - это выбор наиболее оптимальной нейронной сети.
   
5. 
   Посмотрите как даёт определение гиперболического тангенса спикер. Найдите определение в сторонних источниках. Запишите.
   

Элементы теории оптимизации

Эмпиричсекий риск

Риск, ассоциированный с алгоритмом а(х) – это математическое ожидание функционала потерь (ошибки).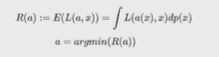



Мы не можем точно посчитать эту величину, но мы можем оценить его при помощи приближения по известной нам тренировочной выборке. Такая оценка называется эмпирическим риском.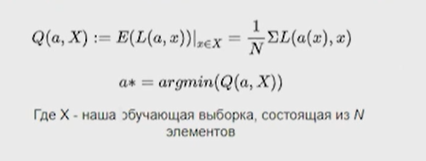



Задача обучения – найти наилучшие параметры, чтобы было ниже значение эмпирического риска.

Три стадии работы с алгоритмом, которые бывают:

1. 
   Выбор модели
   
2. 
   Попытка оценить ошибку на модели
   
3. 
   Попытка найти наилучшие параметры (обучение модели)
   

Те параметры, которые должны быть даны нами в процессе составления программы – гиперпараметры.

Условия Каруша-Куна-Таккера

Используются для решения задач минимизации выпуклых функций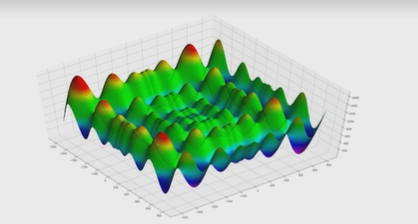





Оптимизация невыпуклых функций представляет собой намного более трудную задачу. Не существует методов, позволяющих гарантированно найти глобальный минимум невыпуклой функции многих переменных. Его может не быть вовсе.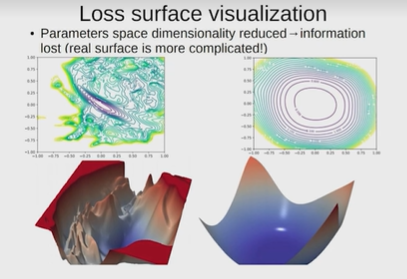



На практике: локальные минимумы очень похожи друг на друга.

На текущий момент ищутся только локальные минимумы.

Чем выше функция, тем хуже работает алгоритм.

Основа целого семейства алгоритмов –градиентный спуск:



Как наклонена? Если производная отрицательная – шаг вправо, если положительная – шаг влево.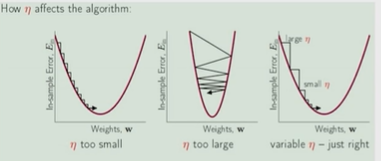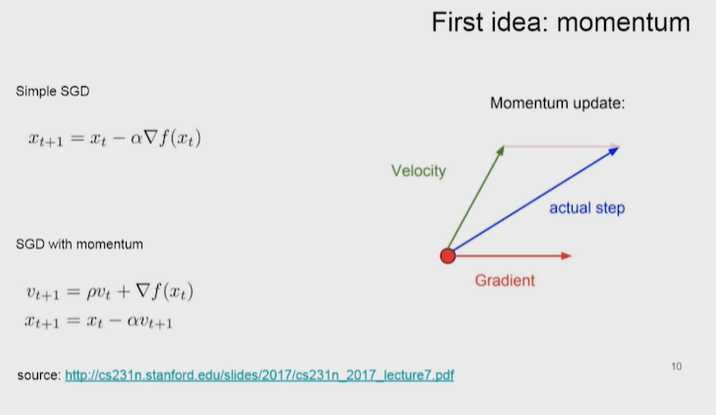





Лернин рейт - Множитель, на который умножаем градиент: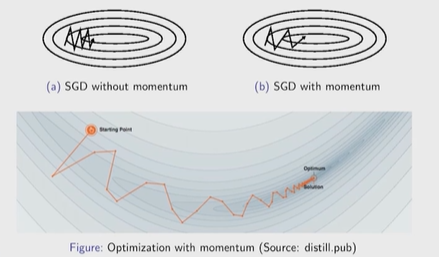



Если дошли до локального оптимума, значит алгоритм сошелся.

Критерий остановки: считаем, насколько на каждом шаге изменяется значение весом. Если не сильно, вполне вероятно, что мы достигли локального минимума. Либо смотрим на модуль градиента. Если он слишком маленький, скорее всего мы вышли на плато достигли локального оптимума.

Как улучшить градиент? Моментум.

Нестеровский градиент: вместо того, чтобы пересчитывать градиенты в текущей точке, посмотрим, какой градиент будет в той точке?



Адаптивный градиентный спуск (adagrad): идея в том, что нужно накапливать историю обновления градиентов по нашим признакам. Каждый раз для расчета нового градиента, нужно запоминать предыдущие значения и складывать их квадраты.

Часто используется в задачах оптимизации, но не используется по дефолту



RMSprop: мы берем и накапливаем сглаженную сумму квадратом за последние несколько шагом, а потом делим на корень из этой величины.



Дефолтный выбор алгоритма (по умолчанию) Adam 2015:

Сочетает в себе adagrad и RMSprop, высчитываем моменты обоих порядком и использует их для вычисления.



Другие оптимизаторы:



Практикум для самостоятельной работы (с ответами)

Задачи:

1. 
   Дайте определение алгоритмическому риску?
   
2. 
   Что такое эмпирический риск?
   
3. 
   Что означает термин выпуклое программирование?
   
4. 
   Что такое градиент?
   
5. 
   Основная цель при использовании метода градиентного спуска?
   

Процесс выполнения:

1. 
   Это среднестатистическая ошибка при выполнении алгоритма машинного обучения.
   
2. 
   Эмпирический риск - это математическое ожидание ошибки тренировочной выборки.
   
3. 
   Выпуклое программирование — это подобласть математической оптимизации, которая изучает задачу минимизации выпуклых функций на выпуклых множествах.
   
4. 
   Градиент - это вектор, состоящий из частных производных функции.
   
5. 
   Это поиск локального минимума или максимума путём мелких итераций. То есть мелкими шагами мы приближаемся к определённому значению функции и отслеживаем изменение значения обоих параметров. Если один из них (или оба) начали с какого-либо шага менять своё значение на противоположное (например сначала х уменьшался, а затем начал увеличиваться), то это означает, что мы прошли определённый локальный минимум. В этом случае применяем отрицательный шаг. Собственно, упрощённо говоря, подбор шага - это и есть главный вопрос теории оптимизации.