1-файл. Что такое числовая последовательность Примеры Определение

• Название: Что такое числовая последовательность Примеры Определение
• Дата: 25.10.2021
• Размер: 50.32 Kb.
• Имя файла: 1-файл.docx
• Тип: Документы; #255140

1. 
   Что такое числовая последовательность? Примеры
   

Определение

Последовательностью называется функция, которая переводит множество натуральных чисел N в некоторое множество X :{xn}={xn}∞n=1={x1;x2;…;xn;…}, xi∈N

Элемент x1 называется первым членом последовательности, x2 - вторым, ... , xn - n-ым или общим членом последовательности
Пример1

Задание. Для последовательности xn={−1;2;5;8;−3;0;…} определить, чему равен третий член x3

Решение. Третьим элементом последовательности будет элемент, идущий третьим по счету, то есть для заданной последовательности имеем, что x3=5

Ответ. x3=5

Задание последовательности формулой ее общего члена

Обычно последовательность целесообразнее задавать формулой ее общего члена, которая позволяет найти любой член последовательности, зная его номер.

Пример 2

Задание. Найти формулу общего члена последовательностиxn={6;20;56;144;352;…}

Решение. Запишем каждый член последовательности в следующем виде:

n=1:x1=6=2⋅3=21⋅3=21⋅(2⋅1+1)

n=2:x2=20=4⋅5=22⋅5=22⋅(2⋅2+1)

n=3:x3=56=8⋅7=23⋅7=23⋅(2⋅3+1)

Как видим, члены последовательности представляют собой произведение степени двойки, умноженной на последовательные нечетные числа, причем два возводится в степень, которая равна номеру рассматриваемого элемента.

Таким образом, делаем вывод, что

xn=2n⋅(2n+1)

Ответ. Формула общего члена: xn=2n⋅(2n+1)

2. 
   Сформулируйте определение предела числовой последовательности.
   

Определение. Число   a   называют пределом числовой последовательности

a₁ ,  a₂ , … a_n , … если для любого положительного числа   ε   найдется такое натуральное число   N ,   что при всех   n > N   выполняется неравенство | a_n – a | < ε .

      Условие того, что число   a   является пределом числовой последовательности a₁ ,  a₂ , … a_n , … , записывают с помощью обозначения

3. 
   Как находится предел числовой последовательности?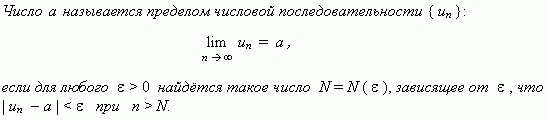
   

Это определение означает, что  a  есть предел числовой последовательности, если её общий член неограниченно приближается к  a  при возрастании  n. Геометрически это значит, что для любого   > 0  можно найти такое число N,  что начиная с  n > N  все члены последовательности расположены внутри интервала ( a - ,a +  ). Последовательность, имеющая предел, называется сходящейся; в противном случае – расходящейся.

Последовательность называется ограниченной, если существует такое число M, что | u_n  |  Mдля всех n .Возрастающая или убывающая последовательность называется монотонной.

4. 
   Как используется число е при начислении сложных процентов?
   

В некоторых случаях — для экономического анализа и в расчетах, связанных с непрерывными про­цессами, в математическом моделировании, а иногда и на прак­тике — возникает необходимость в применении непрерывных процентов.

В финансовой математике увеличение суммы денег в результате начисления сложных процентов определяется формулой:


FV=PV(1+j/m)mn 
где 

PV – исходная сумма денег
FV – наращенная сумма денег
n – число лет, соответствующее сроку финансовой операции
j – ставка процентов за год
m – число периодов начисления в году

Чем больше m, тем чаще начисляются проценты. Способ начисления процентов, при котором m®¥, называется непрерывным начислением процентов.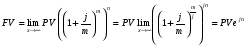 

В этом случае:

Полученную формулу обычно записывают в виде:


где S0 – начальная сумма денег. 

В этой формуле величина δ характеризует скорость роста суммы. Ее называют силой роста, или силой процента. Она равна скорости относительного прироста суммы, т. е. равна относительному приросту суммы за бесконечно малый промежуток времени. 

Задача.

Какая непрерывная ставка заменит поквартальное начисление процентов по номинальной ставке 20%?

Решение: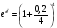

5. 
   Сформулируйте определение ограниченной последовательности.
   

      Последовательность     называется ограниченной сверху, если существует такое число U, что     для любых номеров  n. При этом число U называется верхней границейпоследовательности. 

      Последовательность     называется ограниченной снизу, если существует такое число  L, что     для любых номеров  n. Число  L  называется нижней границейпоследовательности. 

      Последовательность     называется ограниченной, если существуют такие числа  L  и  U, что     для всех  n = 1,2,3,… 

Теорема 1. Любая ограниченная сверху последовательность имеет наименьшую верхнюю границу. 
Теорема 2. Любая ограниченная снизу последовательность имеет наибольшую нижнюю границу.

 

6. 
   Сформулируйте определение неограниченной последовательности.
   

Последовательность {xn}называется неограниченной, если существует такое число M≥0 , что существует такой номер n , что |xn|≥M

7. 
   Приведите пример на ограниченную последовательность
   

Пример 1.

Исследовать последовательность {xn}={1n},n∈N на ограниченность.
Решение. Заданная последовательность является ограниченной, так как для любого натурального номера n выполняются неравенства:

0<1n≤1,∀n∈N

То есть последовательность является ограниченной снизу нулем, и вместе с тем является ограниченной сверху единицей, а значит, является и ограниченной.

Ответ. Последовательность ограничена - снизу нулем, а сверху единицей.
Пример 2. 

Числовая последовательность

1, 4, 9, … n² , … заданная формулой 

x_n = n²,       n = 1, 2, 3, … ,

ограничена снизу, например, числом 0. Однако эта последовательность неограниченна сверху.
      Пример 3.  Последовательность



заданная формулой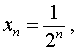 



является ограниченной последовательностью, поскольку для всех   n = 1, 2, 3, …   выполнено неравенство