Главная страница
Навигация по странице:

  • Оборудование

  • 14

  • Собственноручные расчёты

  • Расчёты с использованием программы

  • Исследование влияния сопротивления потерь на характеристики контура

  • Исследование влияния шунтирующего сопротивления на характеристики контура

  • Общий вывод по лабораторной работа

    		•

    5 лаба по отц, 2 курс. Лабораторная работа 5 вынужденные колебания в последовательном контуре


    Скачать 0.99 Mb.
    НазваниеЛабораторная работа 5 вынужденные колебания в последовательном контуре
    Анкор5 лаба по отц, 2 курс
    Дата01.03.2021
    Размер0.99 Mb.
    Формат файлаdocx
    Имя файлаOtchyot_po_laboratornoy_rabote_5.docx
    ТипЛабораторная работа
    #180509

    Ширяев Д.А.

    Студент группы РП-191

    Лабораторная работа № 5

    «ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В ПОСЛЕДОВАТЕЛЬНОМ КОНТУРЕ»

    Цель работы — исследовать явление резонанса и частотные характеристики последовательного колебательного контура; выявить влияние сопротивления потерь и нагрузки на избирательные свойства контура.

    Оборудование – программа моделирования цифровых и электронных схем EWB (ElectronicsWorkbench), программа для математических расчётов MathCAD14, программа для построения математических графиков Graph

    Ход работы:

    1. Изобразим исследуемою схему (рис.1):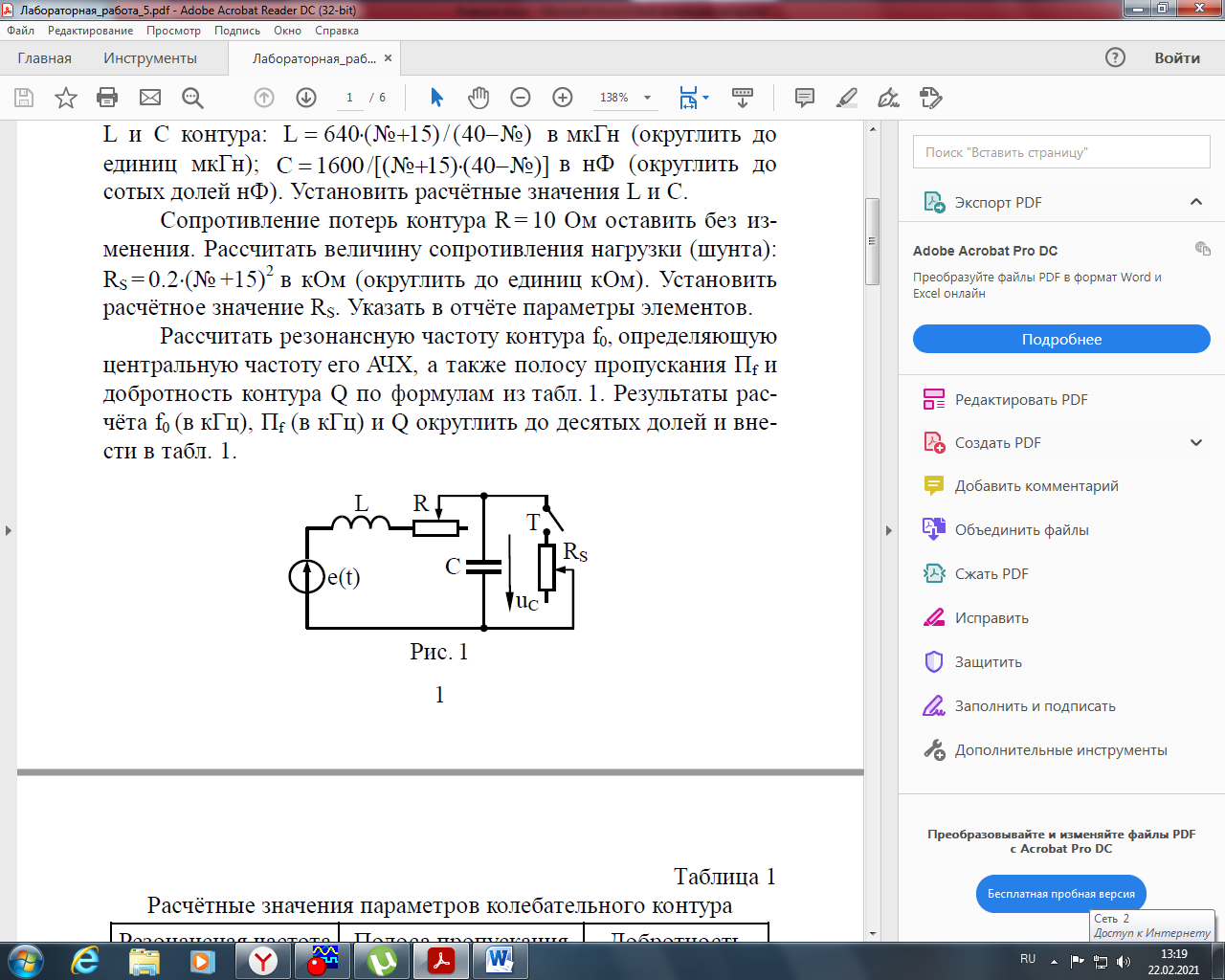



    Рисунок 1 - Схематическое обозначение исследуемой цепи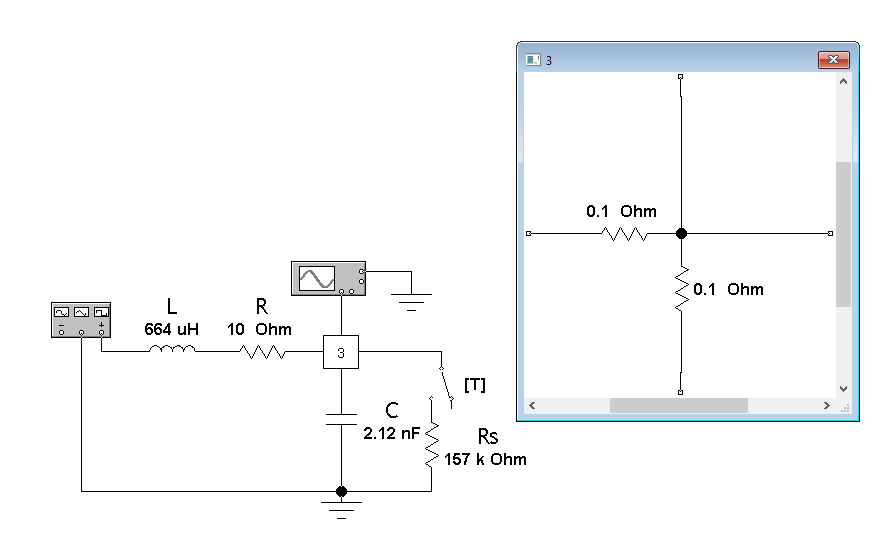



    Рисунок 2 - Исследуемая цепь в программе EWB

    1. По номеру варианта (№16) рассчитал параметры L и C контура, а так же Rs нагрузки (шунта) и установил их расчётные значения. (Расчёты лабораторной работы приведены в 2-х экземплярах: собственноручные и с использованием программы MathCAD14).

    Собственноручные расчёты: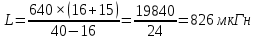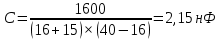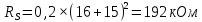







    Расчёты с использованием программы MathCAD14: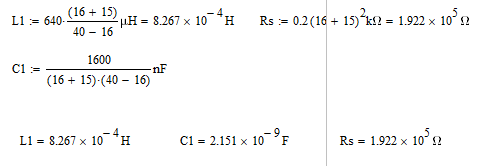



    1. Рассчитал резонансную частоту контура (f0), полосу пропускания (ПF), а так же добротность контура (Q) по формулам. Значения внес в табл.1

    Собственноручные расчёты: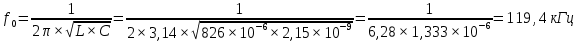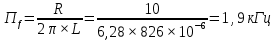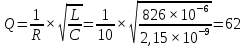







    Расчёты с использованием программы MathCAD14: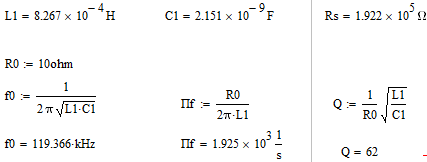



    Таблица 1

    Резонансная частота (fo), кГц
    Полоса пропускания (Пf), кГц
    Добротность (Q)

    119,4
    1,9
    62



    1. Рассчитал значения частот, соответствующие значениям (f0 – k·Пf) и (f0 + k·Пf). Полученные данные внес в табл.2

    Расчёты с использованием программы MathCAD14:



    1. Исследование явления резонанса и частотных характеристик контура

      1. Подал в контур гармонические колебания с частотой, равной расчётному значению резонансной частоты f0, и амплитудой 1В. Тип колебаний – гармонический.




      1. Активировал команду “ACFrequency…” меню “Analysis”. Установил в диалоговом окне команды минимальное и максимальное значение частоты “Startfrequency”, “Endfrequency”; масштаб по оси частот ("Sweeptype") — линейный (Linear); "Numberofpoint" = 2000; масштаб по вертикали ("Verticalscale") — линейный; "Nodesforanalysis" = 3 (напряжение снимается с ёмкости) (рис.3).

    Расчёты с использованием программы MathCAD14: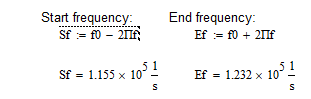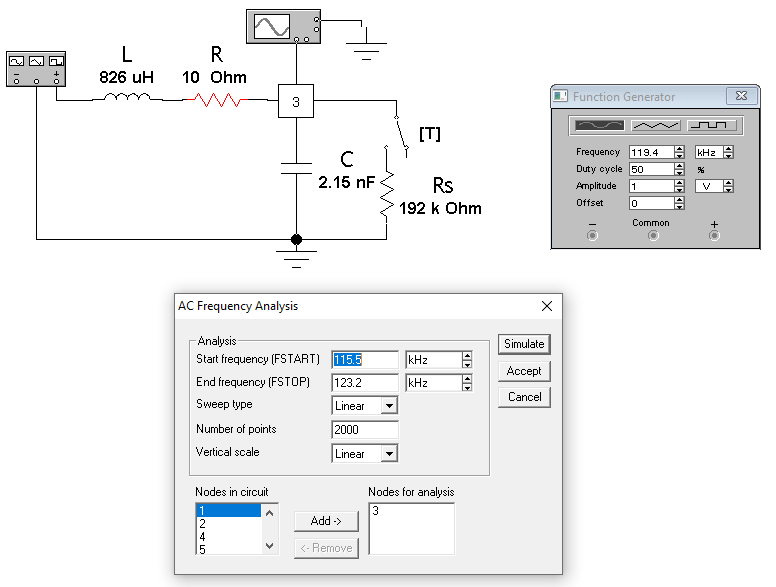





    Рисунок 3 - Активация команды “ACFrequency…”

      1. Используя визиры, снял АЧХ и ФЧХ контура на частотах, указанных в первой строке табл. 2 (рис.4). Полученные данные внес в табл. 2, причём все значения ФЧХ увеличил на 90° и по этим данным построил графики АЧХ (рис.5) и ФЧХ (рис.6).


    Таблица 2

    f, кГц
    115,5
    116,5
    117,4
    118,4
    118,9
    119,4
    119,8
    120,3
    121,3
    122,3
    123,2

    Ku(f)
    15
    19,6
    26,8
    42,2
    53,8
    60,7
    56,6
    45
    27,9
    19,3
    15,8

    Φ(f),◦
    76,2
    71,7
    64,3
    46,5
    28
    1,4
    -20,1
    -41,5
    -61,8
    -72
    -75



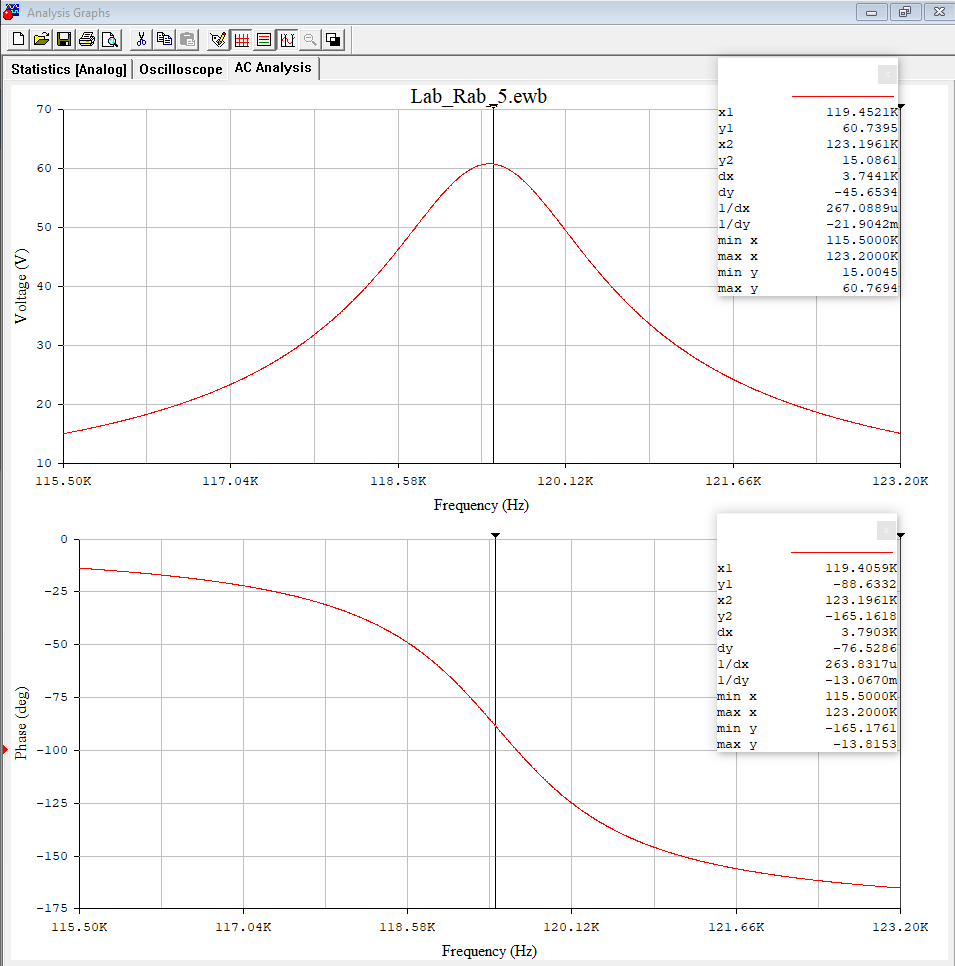    Рисунок 4 - АЧХ и ФЧХ на частоте 119,4 кГц в программе EWB.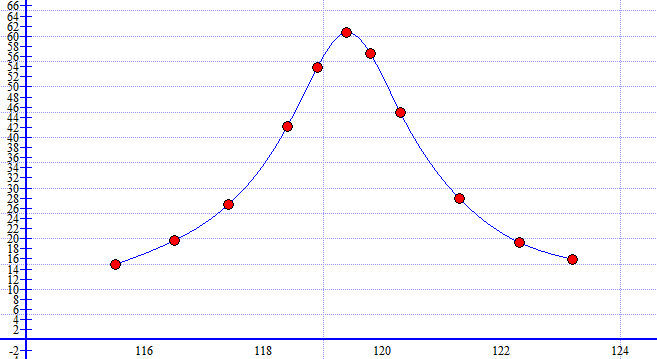
    .

    Рисунок 5 – График АЧХ в программе Graph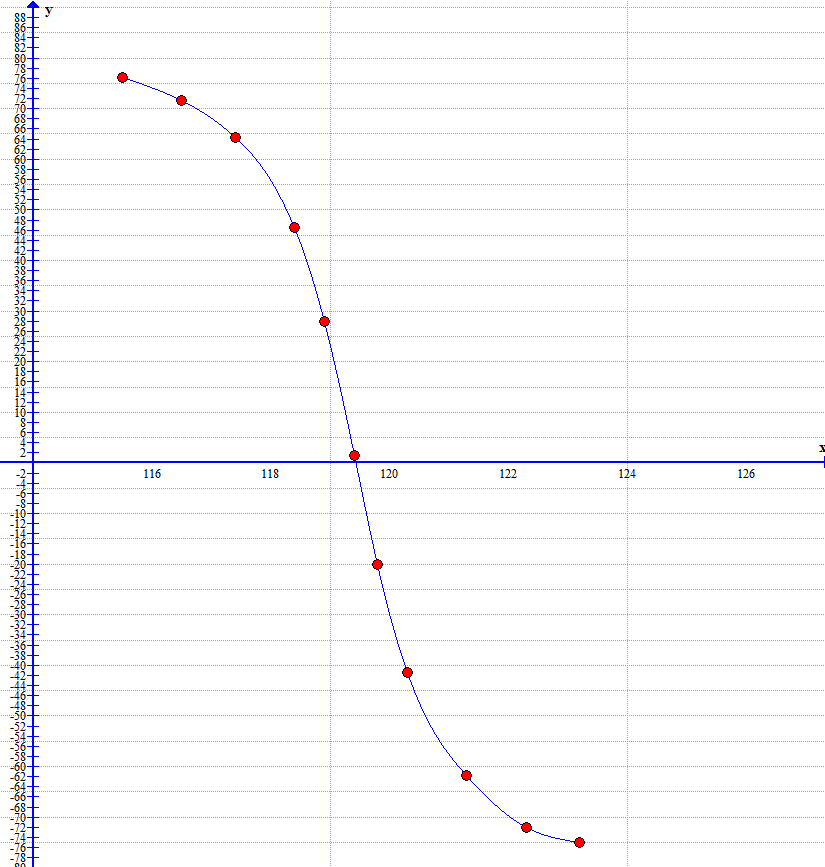


    Рисунок 6 – График ФЧХ в программе Graph

      1. Используя визир, определил по частотным характеристикам экспериментальное значение резонансной частоты контура (рис.7). Внес измеренное значение в табл. 3 и сравнил с расчётным значением резонансной частоты.

    Значения полностью совпали. Причиной погрешности служит необходимое для расчётных вычислений округление значений.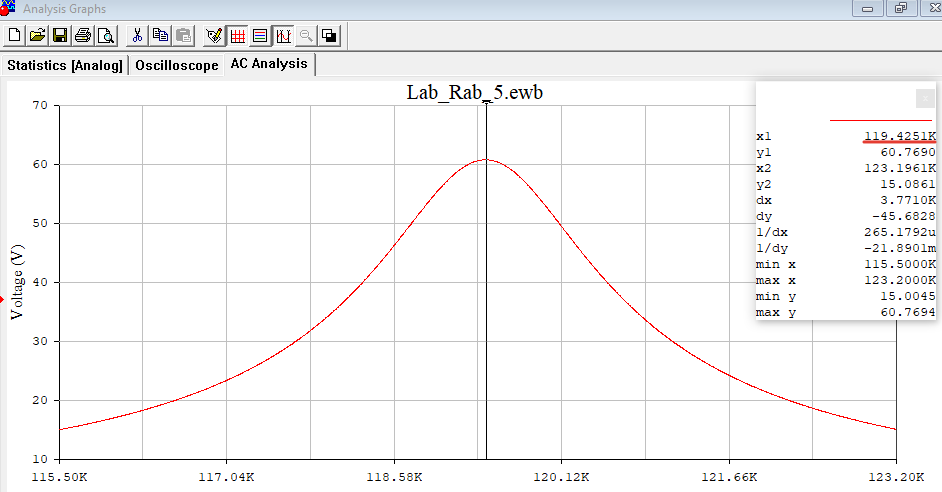


    Рисунок 7 – Резонансная частота f0
    Используя визир, измерил значение АЧХ на резонансной частоте. Так как при единичной амплитуде напряжения источника питания измеренное значение в теории должно совпадать с добротностью контура, будем считать измеренное значение экспериментальной добротностью контура (рис.8). Внес её значение в табл. 3 и сравнить с расчётной добротностью.

    Значения совпали. Это говорит о точности расчетов.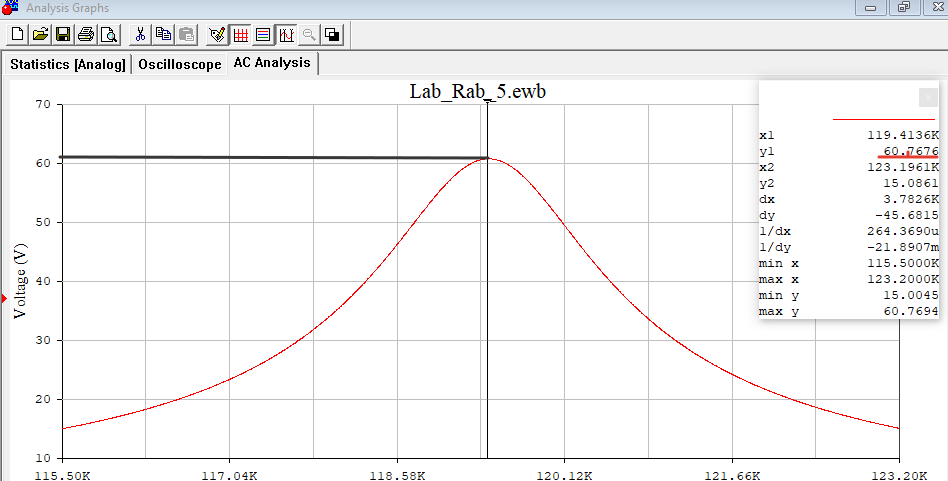



    Рисунок 8 - Добротность Q
    Используя визиры, измерил полосу пропускания контура по уровню 0.707 от максимального значения АЧХ. Внес её значение в табл. 3, сравнил с расчётным значением и указал стрелкой "влево - вправо" на графике АЧХ (рис.9).

    Значения практически совпали. Погрешность обусловлена невозможностью выставления визиры на абсолютно точные значения, вследствие чего и возникают неточности.

    Расчёты с использованием программы MathCAD14: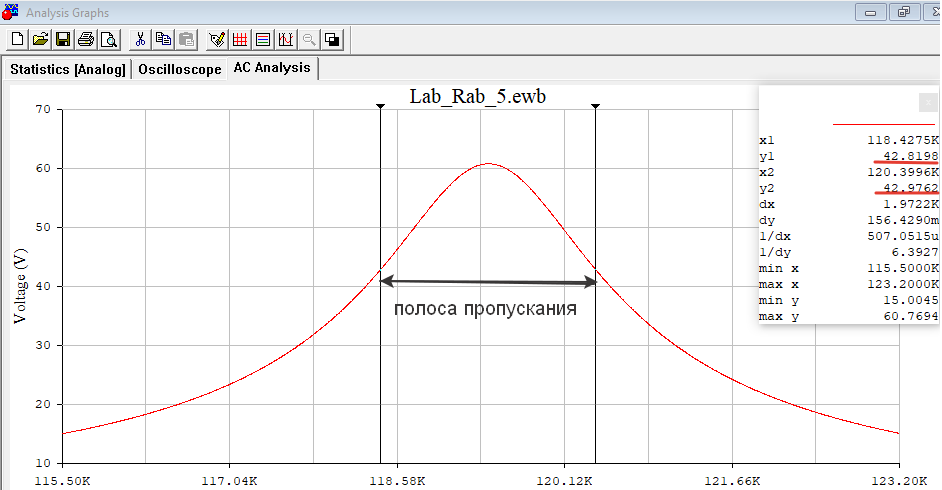




    Рисунок 9 - Полоса Пропускания Пf
    Таблица 3

    Способ получения
    Параметры колебательного контура:

    f0, кГц
    Пf, кГц
    Q

    расчёт
    119,4
    1.9
    62

    измерения
    119,4
    2
    60.7


    Вывод по разделу: в ходе выполнения раздела изучил явление резонанса, а именно: резкое возрастание амплитуды колебаний при частоте, равной или близкой (в нашем случае – равной) к собственной частоте системы. Изучил частотные характеристики контура (АЧХ и ФЧХ) и их изменение.

    1. Исследование влияния сопротивления потерь на характеристики контура

      1. Увеличил величину сопротивления R до 15 кОм.

      2. Снял на тех же частотах АЧХ и ФЧХ контура. Данные внес в таблицу, аналогичную табл. 2 (Табл.4)

    Таблица 4

    f, кГц
    115,5
    116,5
    117,4
    118,4
    118,9
    119,4
    119,8
    120,3
    121,3
    122,3
    123,2

    Ku(f)
    14,5
    18,5
    24,1
    33,6
    38,8
    40,7
    39,4
    34,7
    24,8
    18,2
    14,5

    Φ(f),◦
    70,1
    63,7
    54,4
    35,2
    19,6
    1
    -14,4
    -30,7
    -50,2
    -62,7
    -68,4

    Построил графики АЧХ и ФЧХ контура с увеличенным сопротивлением потерь в одной системе координат с АЧХ и ФЧХ, полученными для исходного значения R (рис.10, 11 и 12).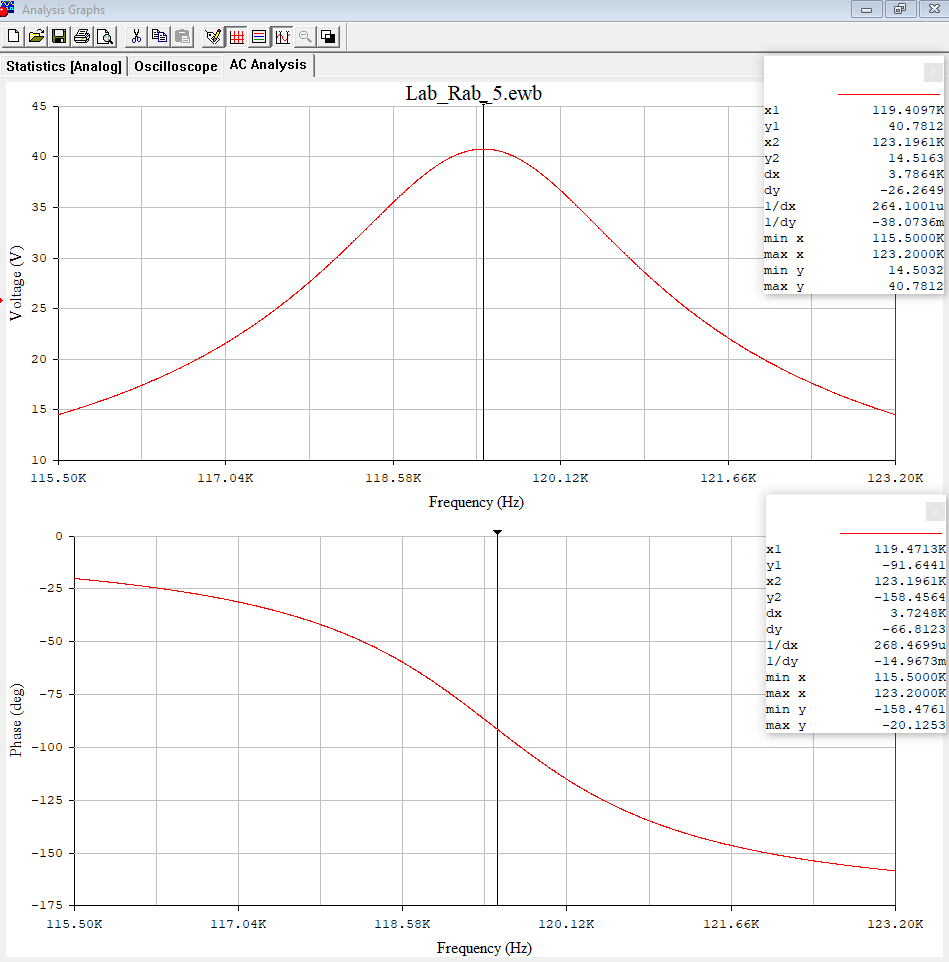


    Рисунок 10 - АЧХ и ФЧХ на частоте 119,4 кГц в программе EWB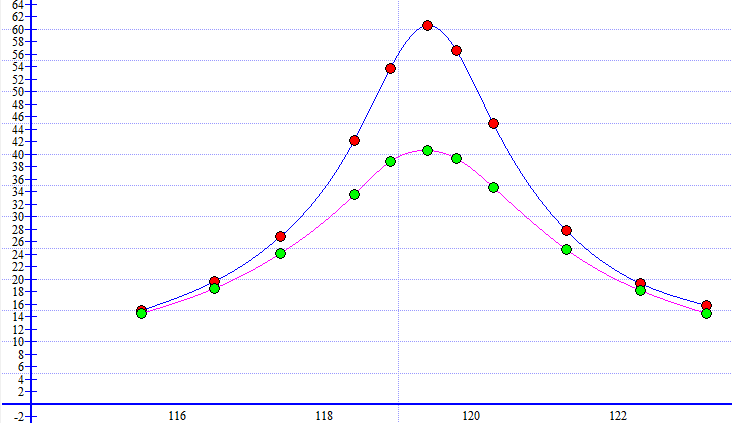




    Рисунок 11 – Графики АЧХ в программе Graph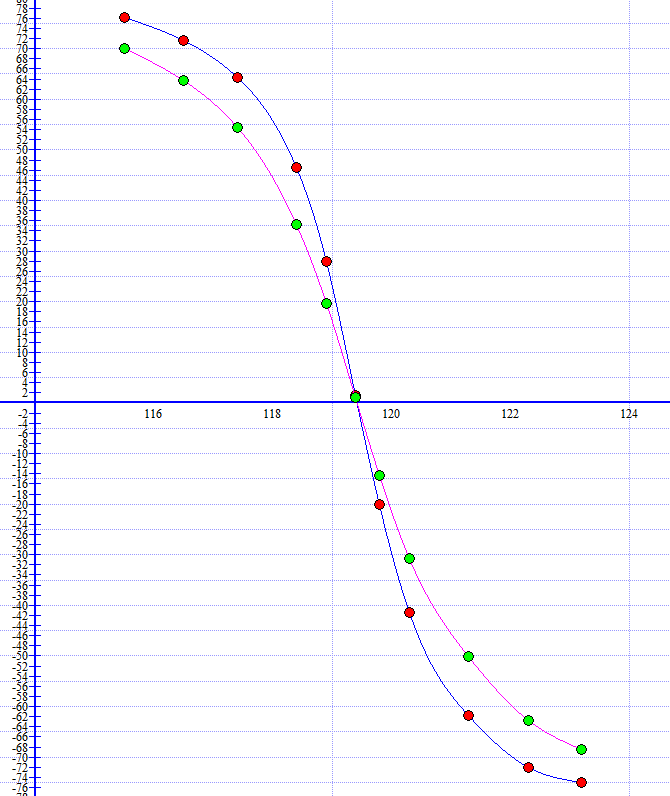



    Рисунок 12 – Графики ФЧХ в программе Graph


      1. С помощью визиров определил по АЧХ резонансную частоту, добротность и полосу пропускания контура. Указал стрелкой полосу пропускания на графике АЧХ (рис.13 и 14). Данные внёс в таблицу и сравнил с предыдущими измерениями.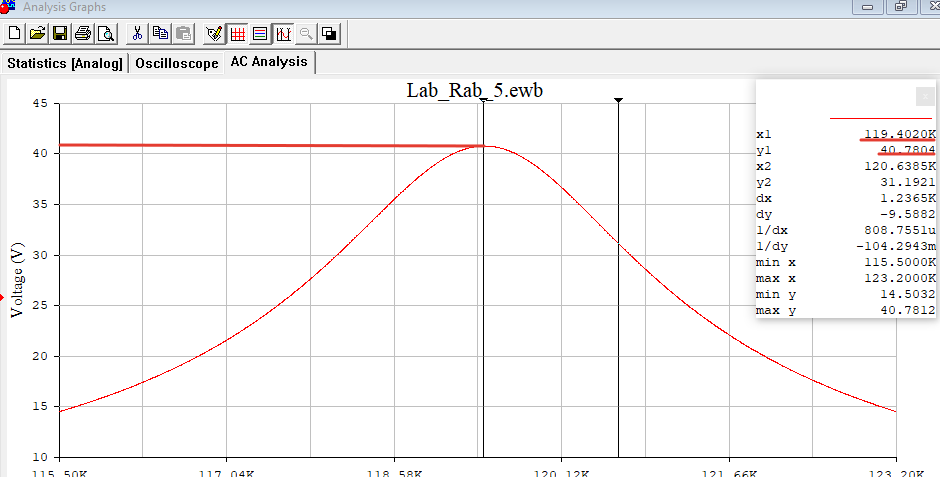



    Рисунок 13 - Резонансная частота (f0) и Добротность (Q)

    Расчёты с использованием программы MathCAD14: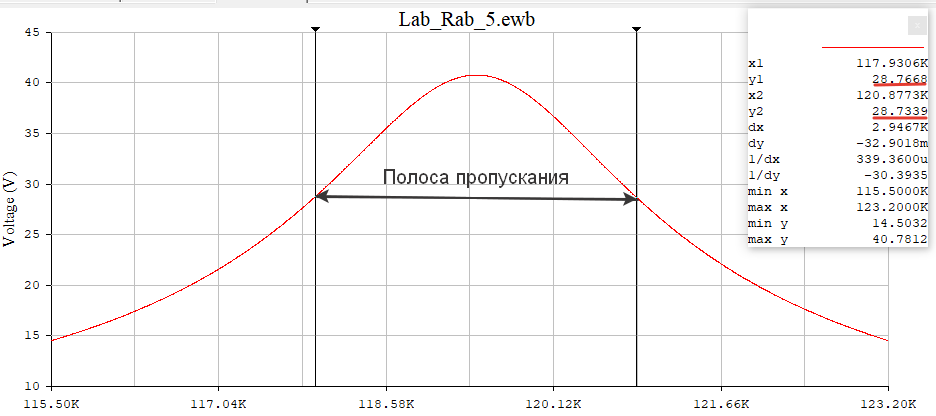





    Рисунок 14 – Полоса пропускания Пf
    Таблица 5

    Способ получения
    Параметры колебательного контура:

    f0, кГц
    Пf, кГц
    Q

    Измерения 1
    119,4
    2
    60,7

    Измерения 2
    119,4
    3
    40.7


    Вывод по разделу: в ходе выполнения раздела исследовал влияние сопротивления потерь на характеристики контура. Показания резонансной частоты остались неизменными. Из-за увеличения потери энергии за каждый период, добротность контура уменьшилась примерно на 33%, следовательно, увеличилось затухание колебаний. Так же, из-за уменьшения максимального значения амплитуды, увеличилась на 50% полоса пропускания контура, что так же указывает на увеличение затухания колебаний.



    1. Исследование влияния шунтирующего сопротивления на характеристики контура




      1. Установил исходную величину сопротивления потерь колебательного контура R = 10 Ом. Замкнул ключ “T”, тем самым подключил шунтирующие сопротивление Rs, имитирующие сопротивление нагрузки (рис.15).




      1. Получил и снял АЧХ контура. Данные внес в таблицу, аналогичную табл. 2.


    Таблица 6

    f, кГц
    115,5
    116,5
    117,4
    118,4
    118,9
    119,4
    119,8
    120,3
    121,3
    122,3
    123,2

    Ku(f)
    14,8
    19,1
    25,7
    38,5
    46,5
    50,8
    48,2
    40,5
    26,7
    19
    14,9

    Φ(f),◦
    73,7
    68,4
    60,2
    41,2
    24,4
    1,1
    -17,4
    -36,5
    -57,6
    -67,5
    -72,4

    Построил в одной системе координат графики АЧХ контура без шунта и с шунтом (рис.16).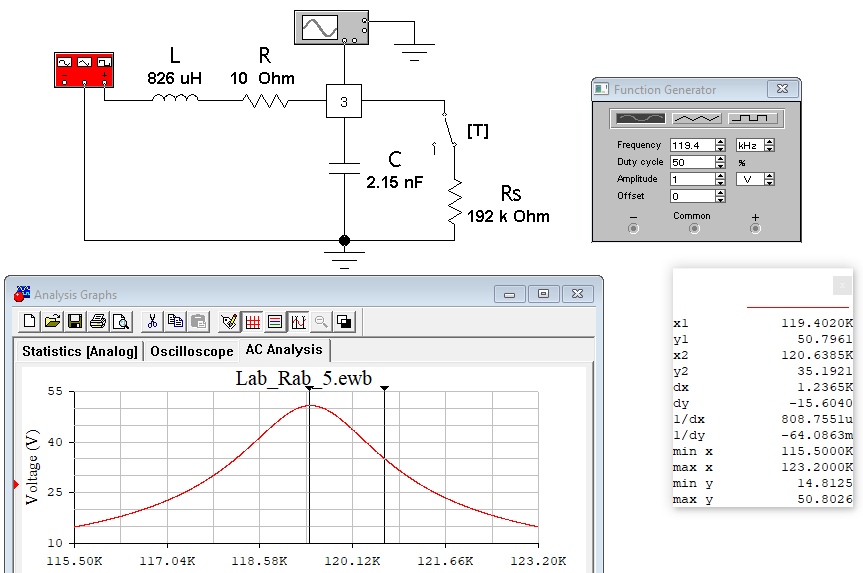

    Рисунок 15 - АЧХ на частоте 119,4 кГц в программе EWB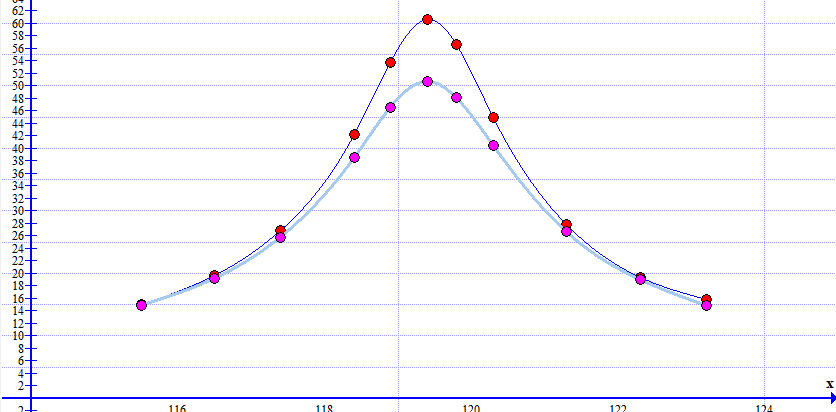

    Рисунок 16 – АЧХ контура без шунта и с шунтом в программе Graph



      1. С помощью визиров определи по АЧХ резонансную частоту, добротность (рис.17) и полосу пропускания (рис.18) нагруженного контура. Результаты внес в табл. 7 и сравнил с данными, полученными в п. 1.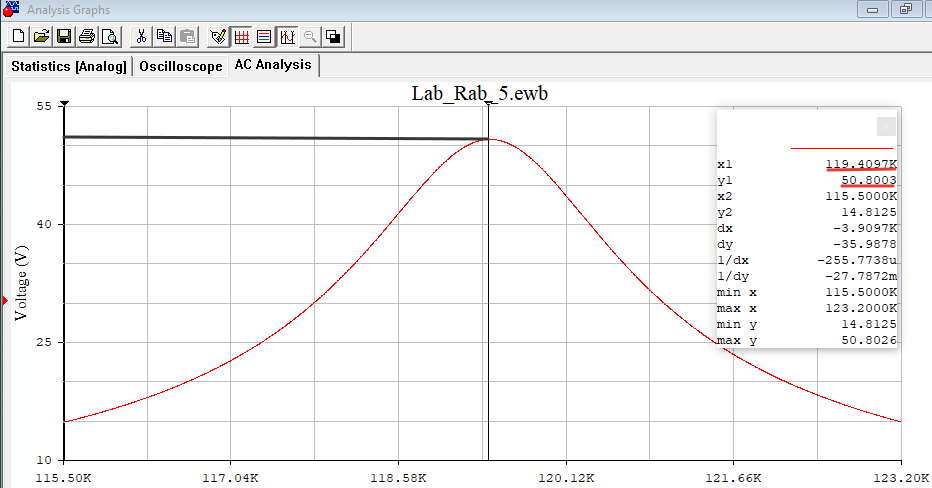



    Рисунок 17 - Резонансная частота (f0) и Добротность (Q)
    Расчёты с использованием программы MathCAD14: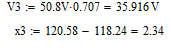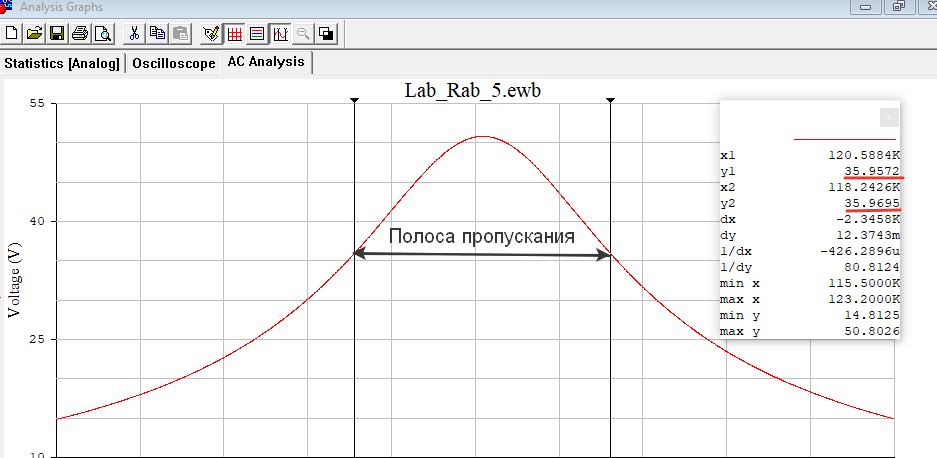




    Рисунок 18 – Полоса пропускания Пf
    Таблица 7

    Условия получения
    Параметры колебательного контура:

    f0, кГц
    Пf, кГц
    Q

    R=10 Ом
    119,4
    1,9
    62

    Rs=192 кОм
    119,4
    2.3
    36


    По результатам измерений, как и при увеличении сопротивления потерь, наблюдали уменьшение значения добротности примерно на 42%, и, как следствие – увеличение значения полосы пропускания на 18%. Это так же говорит об увеличении потери энергии и затухания колебаний.


      1. Установил величину шунтирующего сопротивления равной Rs = 0.1(16 +15) в кОм, после чего установил в окне команды "AC Frequency ..." "Start frequency"= [f0 - (½16+6) Пf], "End frequency" = [f0 + (½16+6) Пf] и в конце получил АЧХ контура (рис.19).

    Расчёты с использованием программы MathCAD14: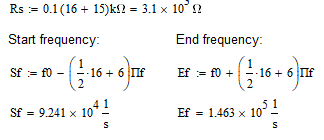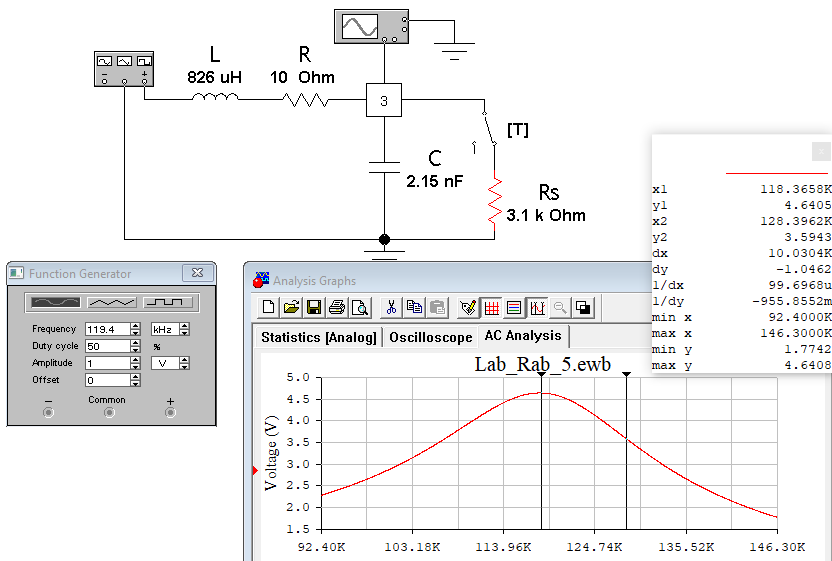




    Рисунок 19 - АЧХ на частоте 118,3 кГц в программе EWB



      1. По АЧХ определил с помощью визиров резонансную частоту, добротность (рис.20) и полосу пропускания контура (рис.21). Результаты внес в табл. 8 и сравнил с предыдущими данными, полученными при отсутствии шунта и исходном значении сопротивления шунта. Сделал вывод о влиянии сопротивления потерь на характеристики контура.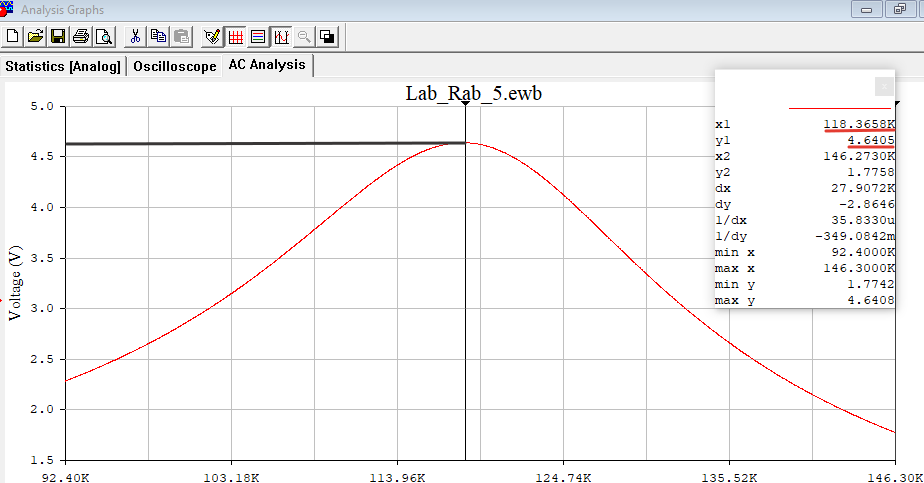


    Рисунок 20 - Резонансная частота (f0) и Добротность (Q)
    Расчёты с использованием программы MathCAD14: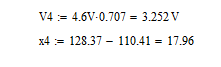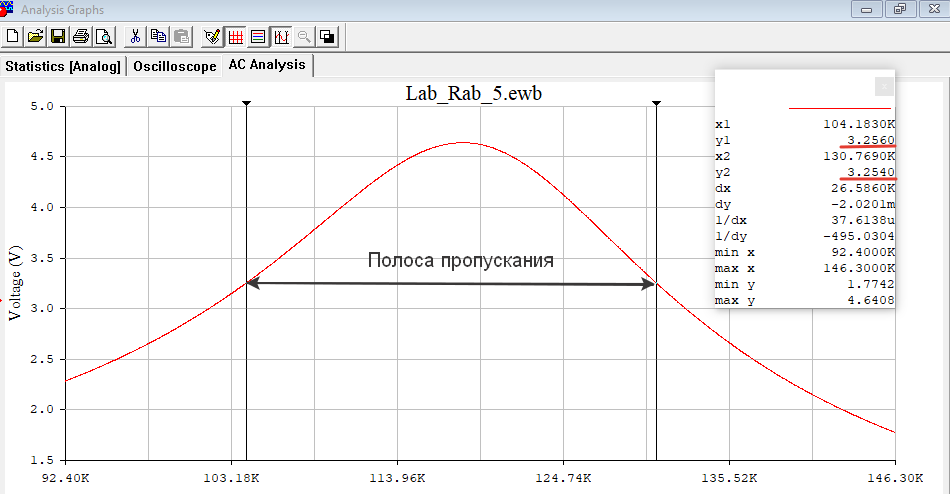



    Рисунок 21 – Полоса пропускания Пf
    Таблица 8

    Условия получения
    Параметры колебательного контура:

    f0, кГц
    Пf, кГц
    Q

    R=10 Ом
    119,4
    1,9
    62

    Rs=192 кОм
    119,4
    2.3
    36

    Rs=3,1 кОм
    118,3
    17,96
    4,6


    По результатам измерений наблюдали сильное уменьшение значения добротности контура (на 92,6%), и, как следствие – сильное увеличение значения полосы пропускания контура (на 88,9% ). Всё это указывает на многократно возросшую потерю энергии контура, а, следовательно, и возросшее затухание колебаний, что мы и можем видеть на графиках АЧХ (рис.22).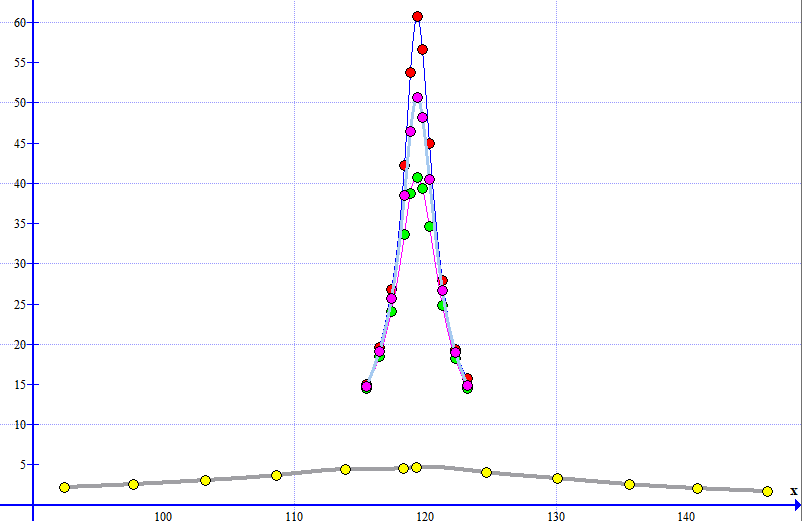


    Рисунок 22 – Графики АЧХ в программе Graph
    Вывод по разделу: в ходе выполнения раздела «исследование шунтирующего сопротивления на характеристики контура», а именно: при подключении шунтирующего сопротивления, имитирующие сопротивление нагрузки, наблюдали увеличение параметров добротности и, как следствие, полосы пропускания контура. Однако, чем меньше шунтирующие сопротивление, тем меньше добротность контура и больше полоса пропускания. Следовательно, чем меньше шунтирующие сопротивление, тем больше потеря энергии в контуре в течение каждого периода.
    Общий вывод по лабораторной работа: в ходе выполнения лабораторной работы исследовал явление резонанса и частотные характеристики последовательного колебательного контура, а так же выявил влияние сопротивления потерь и нагрузки на избирательные свойства контура. Усовершенствовал практические навыки работы в программах EWB и MathCAD14, приобрел навыки работы с программой для построения графиков Graph.

    написать администратору сайта