ЛАБОРАТОРНАЯ РАБОТА №6 ОПРЕДЕЛЕНИЕ РАДИУСА КРИВИЗНЫ ВОГНУТОЙ ПОВЕРХНОСТИ МЕТОДОМ КАТАЮЩЕГОСЯ ШАРИКА. Лабораторная работа 6 определение радиуса кривизны вогнутой поверхности
 Скачать 0.75 Mb. Скачать 0.75 Mb.
|
|
ЛАБОРАТОРНАЯ РАБОТА №6 ОПРЕДЕЛЕНИЕ РАДИУСА КРИВИЗНЫ ВОГНУТОЙ ПОВЕРХНОСТИ МЕТОДОМ КАТАЮЩЕГОСЯ ШАРИКА Выполнил студент гр. _____________ Ф.И.О _________________ Проверил ________________________ дата ___________________ Цель работы: изучить законы движения катающегося по сферической вогнутой поверхности шарика, рассмотреть условия его гармонических колебаний и определить радиус кривизны поверхности Порядок выполнения работы 1  Рис.1 . С помощью микрометра n1 = 5 раз в разных местах измерить диаметр шарика d. Занести данные в Таблицу 1. 2. Вывести шарик из положения равновесия так, чтобы угол отклонения φ (см. рис.1) был мал. Определить время t пяти (n1= 5) полных колебаний шарика. Опыт провести n = 9 раз. Определить период колебаний 3.Вычислить средние значения диаметра 4. Определить случайные отклонения 5. Аналогично вычислить погрешность 5. Вычислить радиус кривизны поверхности 6. Найти абсолютную ∆R и относительную E погрешности в определении R по формулам Данные измерений и вычислений занести в табл. 1-3. Таблица 1.
Контрольные вопросы 1. Из каких составляющих складывается полная энергия шарика? 2. Когда сохраняется полная механическая энергия? 3. Как направлены скорость и ускорение центра масс шарика? 4. Укажите положение шарика, в которых его центр будет иметь: а) максимальное угловое ускорение; б) максимальную линейную скорость; в) тангенциальное ускорение, равное нулю; г) нормальное ускорение, равное нулю; Объясните ваш выбор. 5. Какой вид имеет динамическое уравнение колебаний шарика? 6. Сформулируйте условия, при которых возникают гармонические колебания. 7. Почему угол отклонения шарика (от положения равновесия) должен быть мал?  8. Материальная точка M свободно без трения скользит в поле силы тяжести по гладким стенкам симметричной ямы (A и B – наивысшие точки подъема). При этом величина тангенциальной (касательной к траектории) проекции ускорения точки М: а) отлична от нуля в точке В; б) максимальна в нижней точке траектории О; в  ) равна нулю в точке А; г) одинакова во всех точках траектории; ) равна нулю в точке А; г) одинакова во всех точках траектории;9. Материальная точка M движется по окружности со скоростью а) 1 б) 2 в) 3 г) 4 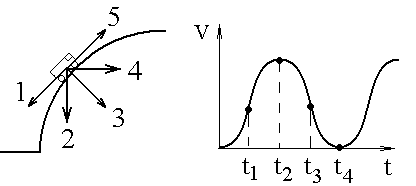 10. Из-за неисправности мотора величина скорости автомобиля синусоидально изменялась во времени, как показано на графике зависимости V(t). В момент времени t1 автомобиль поднимался по участку дуги. Куда может быть направлена результирующая всех сил, действующих на автомобиль в этот момент времени? 10. Из-за неисправности мотора величина скорости автомобиля синусоидально изменялась во времени, как показано на графике зависимости V(t). В момент времени t1 автомобиль поднимался по участку дуги. Куда может быть направлена результирующая всех сил, действующих на автомобиль в этот момент времени?1) 1 2) 2 3) 3 4) 4 5) 5  11. Небольшая шайба начинает движение без начальной скорости по гладкой ледяной горке из точки А. Сопротивление воздуха пренебрежимо мало. Зависимость потенциальной энергии шайбы от координаты х изображена на графике 11. Небольшая шайба начинает движение без начальной скорости по гладкой ледяной горке из точки А. Сопротивление воздуха пренебрежимо мало. Зависимость потенциальной энергии шайбы от координаты х изображена на графике а) в 2 раза больше, чем в точке В б) в 2 раза меньше, чем в точке В в) в 1,75 раза больше, чем в точке В г)в 1,75 раза меньше, чем в точке В  12. На рисунке показан график зависимости потенциальной энергии а)  в) в) 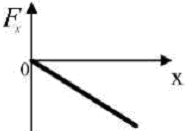 г) г) Литература Савельев И.В. Курс общей физики. т.1. М:Наука, 1986.- гл.I, §4, гл.III, §24, гл.V, §41-43, 53 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
