вариант 2. Лабораторная работа 6 Средние величины. Применение средних величин для оценки общественного здоровья.

• Название: Лабораторная работа 6 Средние величины. Применение средних величин для оценки общественного здоровья.
• Анкор: вариант 2
• Дата: 18.05.2022
• Размер: 35.46 Kb.
• Имя файла: variant_2.docx
• Тип: Лабораторная работа; #535580

ПЕНЗЕНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
МЕДИЦИНСКИЙ ИНСТИТУТ
Кафедра гигиены, общественного здоровья и здравоохранения

Лабораторная работа №6

«Средние величины. Применение средних величин для оценки общественного здоровья.»

Вариант №2

Выполнил: студентка 3 курса гр. 19лл13

Евсеева Т. Е.

Проверила: Пугачева О. В.

Пенза 2022

Задание 1: Обработка вариационного ряда, вычисление средней арифметической (М), среднего квадратического отклонения () и ошибки средней (m).

1. 
   Вычислить среднюю арифметическую (М) по способу моментов. Порядок вычисления должен быть представлен в виде таблицы. За условную среднюю (М₁) следует принимать варианту с наибольшей частотой;
   
2. 
   Вычислить среднее квадратическое отклонение () и ошибку средней (m).
   

Определить средний рост 14-летних девочек при наличии следующих данных

Рост в см (V)	Число девочек (Р)
140-144	20
145-149	30
150-154	85
155-159	35
160-164	15

Решение: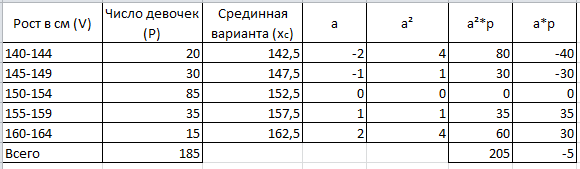



A=152,5 ; n=185

y= 145-140=5

– средняя арифметическая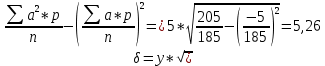

– среднее квадратичное отклонение

– ошибка средней

Ответ: 5,26±0,39

Задание 2: Сравнение средних величин (или показателей)
У студентов-медиков проводилось исследование пульса до и после сдачи экзамена.

Частота пульса в среднем до экзамена составила 98,44,0, после экзамена – 84,05,0 ударов в минуту.

Можно ли на основании этих данных считать, что после сдачи экзаменов частота пульса снижается и приближается к норме?

Решение: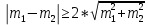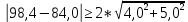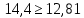





; - верно

Ответ: неравенство выполнено верно, значит, на основании этих данных можно считать, что после сдачи экзаменов частота пульса снижается и приближается к норме.

Задание 3: Определение достоверности средних величин при малом числе наблюдений
При определении скорости кровотока получены следующие данные: 30, 19, 21, 32, 24, 24, 25 см/с.

Вычислить среднюю скорость кровотока (М) и определить достоверность среднего результата (m) при доверительной вероятности (Р) 0,95 (95 %).

Решение:



; - среднее квадратичное отклонение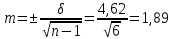

; - ошибка средней арифметической величины



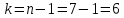Если Р =0.95 (95%), тогда t=2,4



Ответ: средняя скорость кровотока (М) у 7 обследованных равна 25.

При проведении повторных исследований в 95% случаев будет колебаться в пределах 25±4,53, то есть от 20,47 до 29,53.
Задание 4: Определения необходимого объема наблюдений
Определить необходимое для исследования число детей 15 лет для получения среднего роста с точностью до 0,5 (0,5) при доверительной вероятности (Р) 0,95.

При пробном исследовании 10 детей установлено, что среднее квадратическое отклонение () равно 3,5 см.

Решение:

Если P=0.95, то t=2



Ответ: необходимо сделать 196 дополнительных наблюдений для получения среднего роста с точностью до 0,5 (0,5) при доверительной вероятности (Р) 0,95.