Тема средние величины. Назначение средних величин. Виды средних величин

• Название: Тема средние величины. Назначение средних величин. Виды средних величин
• Дата: 04.02.2023
• Размер: 231.5 Kb.
• Имя файла: statistika_6-9.doc
• Тип: Закон; #920096

ТЕМА 6. СРЕДНИЕ ВЕЛИЧИНЫ.
1. Назначение средних величин.

2. Виды средних величин.

3. Свойства средних величин.

4. Структурные средние величины (мода и медиана).
Вопрос 1.

Характеристика признаков явлений или общих целей, общих закономерностей процесса, являющейся важнейшей социально-экономической задачей решается при помощи средних величин. Однако эта общая задача должна быть конкретизирована более частными задачами. В экономике можно выделить несколько основных вопросов, решение которых связано с вычислением средних величин:

• 
  характеристика уровня развития явления
  
• 
  сравнение двух или нескольких уровней
  
• 
  характеристика изменения уровня, явлений во времени
  
• 
  выявление и характеристика связей и закономерностей развития явления
  
• 
  производство расчетов и их оценка в связи с планированием, прогнозированием, балансовыми расчетами и т.д.
  

С помощью средних величин проводится много аналитических исследований при решении народнохозяйственных задач в целом или по отраслям, когда приводятся важнейшие характеристики состояния и развития отрасли, предприятия и т.д. «Аналитическая сила» средних величин состоит в обобщении соответствующей совокупности типичных, однородных показателей, явлений, процессов. Они позволяют переходить от единичного к общему, от случайного к закономерному, сглаживая различая в величине признака, которые возникают по тем или иным причинам у отдельных единиц наблюдения.

Применение средних позволяет охарактеризовать определенный признак совокупности одним числом, несмотря на количественные различия единиц по данному признаку внутри совокупности. Средняя - это величина абстрактная, а не конкретная, т.к. в ней сглаживаются отдельные значения единиц совокупности, имеющие отклонения в ту или иную сторону.
В опрос 2. Средней величиной называется обобщающая количественная характеристика однородных явлений по какому - либо варьирующему признаку.

Средняя величина (Х) представляет собой отношение абсолютного статистического показателя, который выражает общий объем явлений или признака, к численности совокупности этого явления. Индивидуальные значения признака называются вариантами этого признака и обозначаются Х, а число единиц совокупности, которые указываю на их повторение называются частотами (f) или весами (W).
Различают следующие виды средних величин:

• 
  средняя арифметическая
  
• 
  средняя гармоническая
  
• 
  средняя геометрическая
  
• 
  средняя квадратическая
  
• 
  структурные средние - мода и медиана.
  

В теории статистики различают следующие формы средних величин:

• 
  простая форма (не взвешенная)
  
• 
  сложная (взвешенная)
  

Средняя арифметическая - наиболее распространенный вид средней, которая может быть выражена при помощи формул:

1. 
   Простая средняя арифметическая исчисляется тогда, когда индивидуальные значения вариантов встречаются по одному или одинаковому числу раз, т.е. когда повторяемость каждого варианта одинакова:
   

где Х – отдельные варианты признака, n - число единиц в совокупности

2. 
   Взвешенная средняя арифметическая исчисляется тогда, когда отдельные значения признака повторяются, встречаются по несколько раз
   

где Х – отдельные варианты признака, n - число единиц в совокупности, f – частоты

Частоты принято называть весами, поэтому средняя арифметическая, вычисленная с учетом весов, и получила название взвешенной.
В статистической практике бывают случаи, когда при вычислении средней имеются данные об индивидуальных значениях признака (Х) и его общем объеме в совокупности (w), но не известны частоты (f). В таких случаях среднее значение признака исчисляется по формуле средней гармонической, которая представляет собой величину, обратную средней арифметической из обратных значений вариант.

1. 
   Простая средняя гармоническая имеет следующий вид: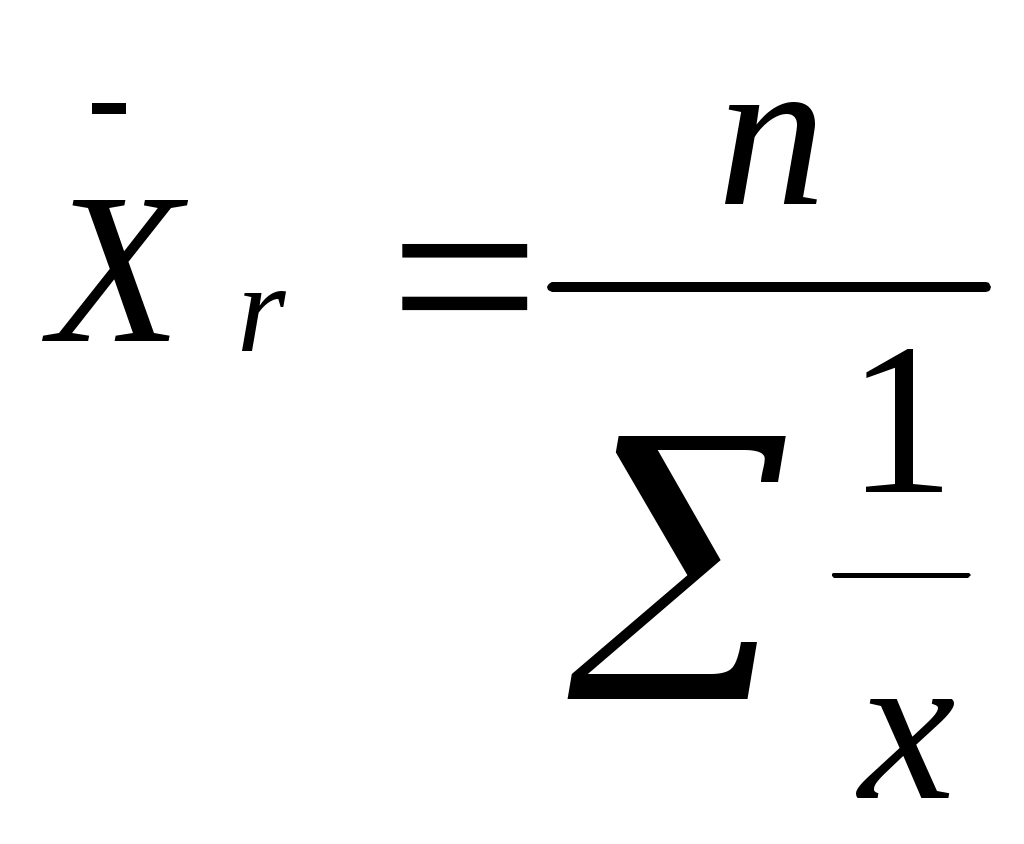
   

2. Взвешенная средняя гармоническая выражается формулой: 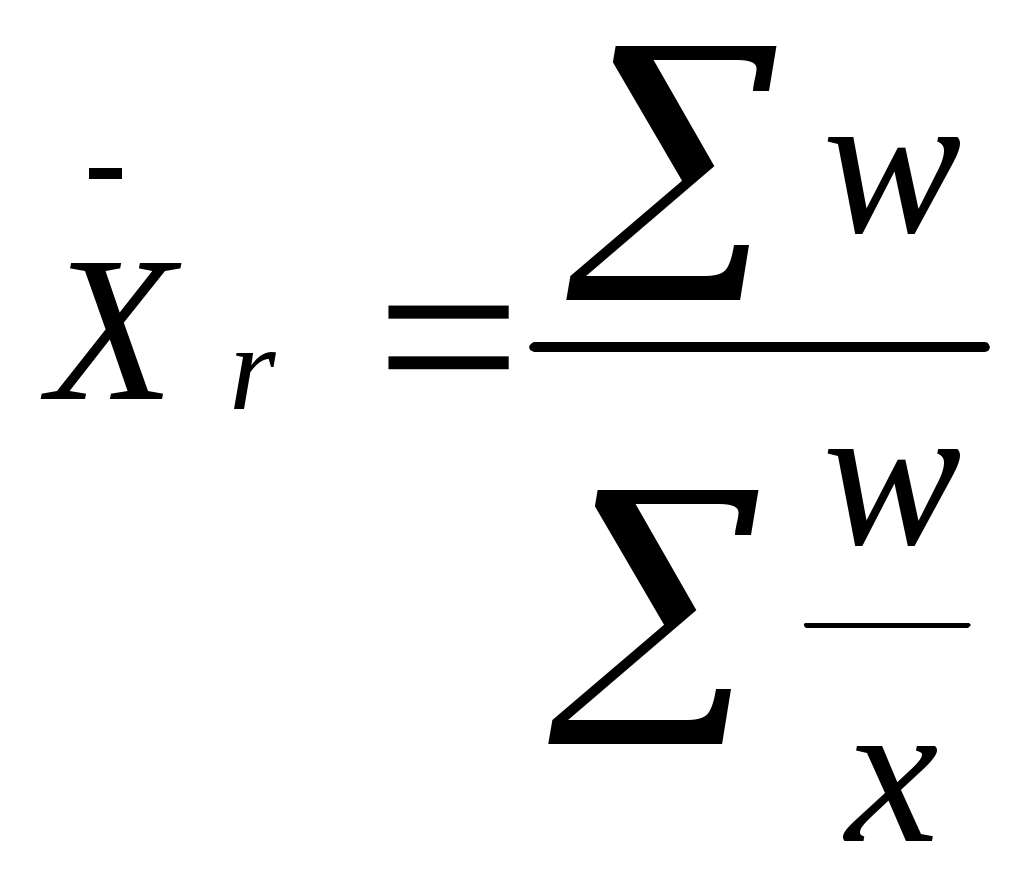где w - объем явления. W = Х * f
Средняя геометрическая величина применяется при расчетах средних темпов роста для рядов динамики и имеет следующий вид:
Средняя квадратическая величина применяется для оценки вариации признака от среднего уровня, при расчете среднего и квадратического отклонения и дисперсии, при расчете коэффициента вариации.

1. 
   Простая средняя квадратическая определяется по формуле:
   

2. 
   Взвешенная средняя квадратическая: .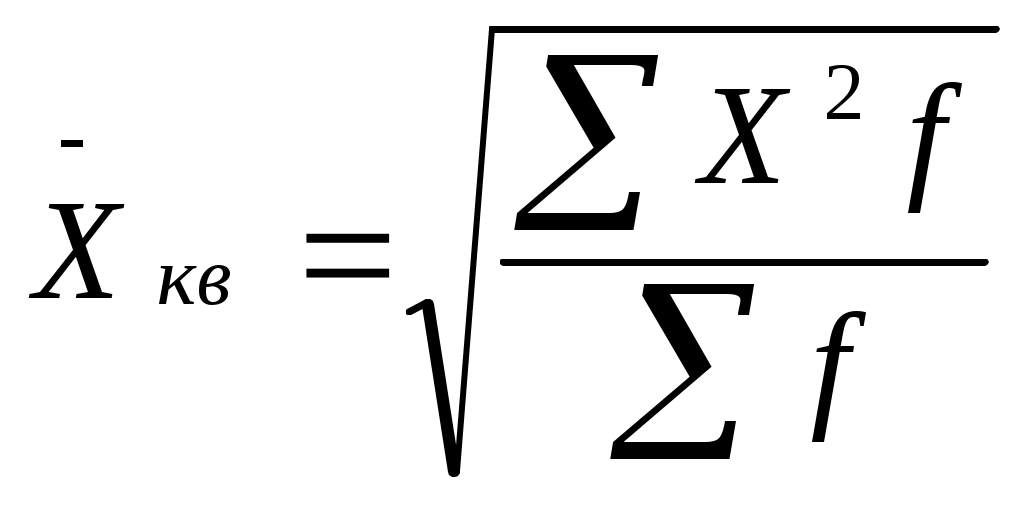
   

Средняя хронологическая величина – средний уровень ряда динамики, т.е. средняя, вычисленная по совокупности значений показателя в разные моменты или периоды времени. Она используется, только если значения показателя представлены за равные промежутки времени.
x₁ + x₂ + x₃ + x_n

X = ______________________

n – 1
Вопрос 3.

Важнейшими свойствами средних величин являются следующие:

1. 
   Сумма отклонений индивидуальных значений признака как от простой, так и от взвешенной средней всегда равна нулю: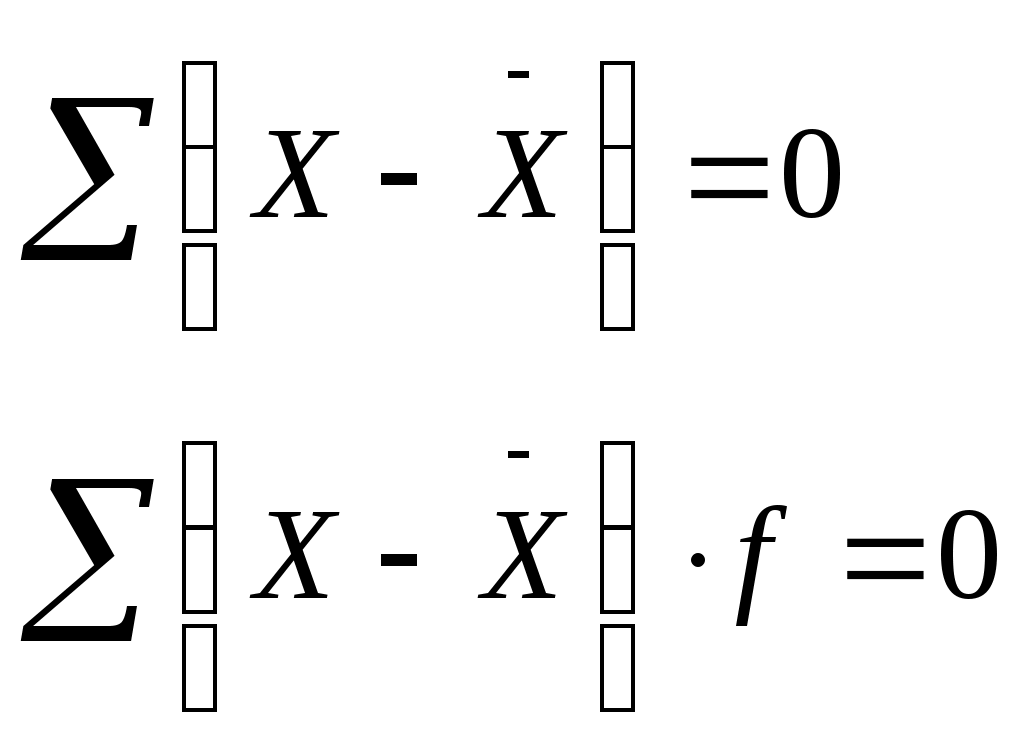
   

Это свойство используется для контроля правильности вычислений средней арифметической.

3. 
   Если все варианты уменьшить или увеличить на одно и тоже число а, то средняя величина уменьшится или увеличится на это же число а:
   

4. 
   Если варианты признака уменьшить или увеличить в а раз, то средняя увеличится или уменьшится в это же число раз:
   

5. 
   Если все частоты увеличить или уменьшить в какую-то величину d, то средняя от этого действия не изменится:
   

Увеличение(уменьшение) всех весов в несколько раз приводит к тому, что во столько же раз изменится и числитель и знаменатель дроби, поэтому значение дроби не изменяется.

Вопрос 4.
Для характеристики структуры совокупности применяются особые показатели, которые можно назвать структурными средними.

К таким показателям относятся мода и медиана.

Модой или модальной величиной признака в ряду распределения является варианта, имеющая наибольшую частоту.

В дискретном ряду мода – это варианта с наибольшей частотой.
Ряд распределения женской кожаной обуви магазина:

Размер кожанной обуви (х)	35	36	37	38	39	40	41
Число покупателей (f)	5	47	60	54	33	12	9

В данном дискретном ряду модой будет являться 37-й размер обуви, так как он имеет наибольшую частоту покупки (60 раз)).

В интервальном ряду мода определяется по формуле:

,

где Х₀ - нижняя граница или минимальная граница модального интервала.

i - величина модального интервала;

f ₁ - частота интервала, предшествующего модальному;

f ₂ - частота модального интервала;

f ₃ - частота интервала, следующего за модальным.

Модальный интервал – это интервал, который имеет наибольшую частоту;
Медиана – это срединное значение признака, которое делит ряд на равные части. Одна часть единиц варьирующего ряда имеет значение варьирующего признака меньше, чем медиана, другая часть - больше.

Для дискретного ранжированного ряда (т. е. построенного в порядке возрастания или убывания индивидуальных величин) с нечетным числом членов медианой является варианта, расположенная в центре ряда. (Например, пусть мы имеем сведения о стаже работы 5 продавцов магазина: 1, 2, 5, 6, 9 лет. Данный ряд является ранжированным с нечетным числом членов (5 продавцов). Для данного ряда медиана будет равна 5 годам, так как ею в данном ряду является серединная, т.е. 3-я варианта со стажем работы 5 лет.)

Для дискретного ранжированного ряда с четным числом членов медианой будет варианта рассчитанная из двух смежных центральных вариант. (Например, пусть мы имеет сведения о стаже работы 6 продавцов магазина: 1, 3, 4, 5, 7, 9 лет. Данный ряд является ранжированным с четным числом членов (6 продавцов). В этом ряду медиана будет рассчитываться как средняя арифметическая простая из двух смежных центральных вариант, которыми являются стаж работы 4 года и 5 лет. Тогда медиана для данного ряда будет равна (4+5)/2 =4,5 года
Для интервального вариационного ряда медиана будет определяться по формуле: ,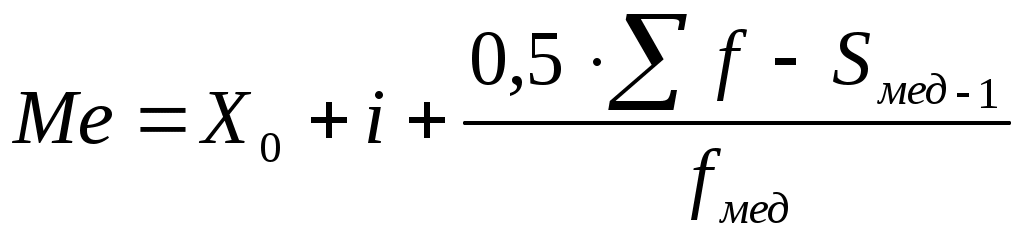
где Х₀ - нижняя граница медианного интервала.

i – величина медианного интервала;

- сумма частот ряда;

- сумма накопленных частот в интервалах, предшествующих медианному;

- частота медианнного интервала.

Медианный интервал – это интервал, который содержит единицу, находящуюся в середине ранжированного ряда.


ТЕМА 7. ПОКАЗАТЕЛИ ВАРИАЦИИ.
1. Вариация признаков и причины ее порождающие.

2. Показатели вариации и их значение в статистике.

Вопрос 1.

Различия индивидуальных значений признака внутри изучаемой совокупности называется вариацией признака. Она возникает в результате того, что индивидуальные значения признака складываются под совокупным влиянием разнообразных факторов, которые по-разному сочетаются в каждом отдельном случае.

Средняя величина является обобщающей характеристикой признака изучаемой совокупности, но она не показывает строение совокупности. Средняя величина не дает представления о том, как отдельные значения изучаемого признака группируются вокруг средней, сосредоточены ли они вблизи или значительно отклоняются от нее.

Если отдельные варианты недалеко отстоят от средней, то мы говорим, что данная средняя хорошо представляет изучаемую совокупность. Для того чтобы изучить, как велики эти отклонения, их измеряют при помощи показателей вариации.
Вопрос 2.

Ряд распределения, образующийся в результате накопления статистической информации по значению варьирующего признака, является наиболее фундаментальной характеристикой совокупности. Он дает наиболее полное представление о результатах действия и взаимодействия всех факторов явления (основных и случайных), о сложившихся под их влиянием закономерностей ряда распределения, о свойствах индивидуальных значений признака и их особенностях. Изучение ряда распределения позволяет установить связь единичного и массового, частного и общего, случайного и закономерного.

Для более глубокого изучения ряда распределения варьирующего признака служат следующие показатели вариации:

1. Размах вариации, который представляет собой разность между максимальным и минимальным значением признака, т.е. амплитуду колебания вариации в ряду распределения.

2. 
   Среднее линейное отклонение представляет собой среднюю величину из абсолютных отклонений вариант признака от средней и рассчитывается по формуле:
   

невзвешенное ,
взвешенное .

Среднее линейное отклонение выражается в тех же единицах измерения, что и сам признак. Среднее линейное отклонение дает приблизительную оценку вариации признака в рядах распределения, т.к. не учитывает колебаний признака в ряду. Для более точной оценки вариации признака в ряду распределения служит дисперсия или средний квадрат отклонения.

3. 
   Дисперсией называется средний квадрат отклонений индивидуальных значений признака от их средней величины. Рассчитывается по формуле:
   

простая ,

взвешенная .

4. 
   Среднее квадратическое отклонение характеризует абсолютный размер колеблемости признака около средней, показывает, насколько в среднем отклоняются отдельные значения признака от среднего их значения.
   

простое ,

взвешенное .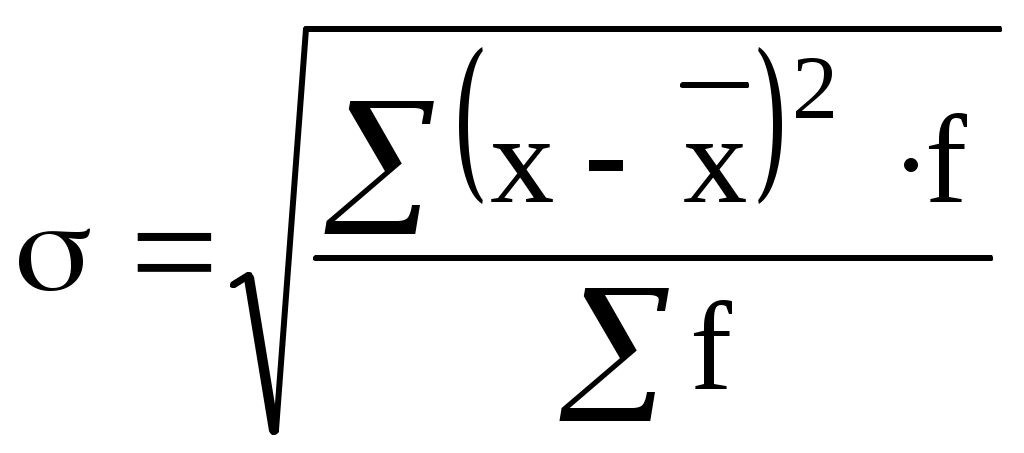

Среднее квадратическое отклонение показывает отклонение различных индивидуальных значений признака в ряду распределения от среднего уровня. Измеряется в тех же единицах, что и сам признак. Среднее квадратическое отклонение является более точной характеристикой вариации признака в ряду распределения по сравнению со средне линейным отклонением, т.к. учитывает внутренние колебания признака в ряду распределения.
5. Коэффициент вариации признака в совокупности представляет собой относительную колеблемость признака в совокупности, и рассчитывается по формуле:

• 
  по среднелинейному отклонению ;
  
• 
  по среднеквадратическому отклонению
  

Коэффициент вариации показывает на сколько % отклоняется индивидуальное значение признака в ряду распределения от среднего уровня. Допустимые пределы колебания признака в ряду приблизительно 33%, тогда совокупность признается однородной. Если эти пределы превышаются то данная совокупность должна быть подвергнута преобразованию с целью приведения к нормальному распределению.

ТЕМА 8. ИНДЕКСЫ.

1. Понятие индекса. Основные элементы индекса.

2. Классификация индексов.

3. Взаимосвязь между индексами.

Вопрос 1.

Индекс (index) латинского происхождения и переводится как указатель, показатель. В статистике индексами называют относительные показатели, характеризующие изменение во времени или в пространстве сложных общественных явлений, элементы которых не поддаются непосредственному суммированию.

Для характеристики изменений таких сложных явлений применяют индексы различных видов и форм, построенные на основе абстрагирования, выявления и установления причинно-следственных связей и отношений.

Для определения индекса надо произвести сопоставление не менее двух величин. При изучении динамики социально-экономических явлений сравниваемая величина (числитель индексного отношения) принимается за текущий (или отчетный) период, а величина, с которой производится сравнение, - за базисный (плановый) период.

Результат расчета индекса может выражаться в коэффициентах или процентах (например индекс цен равен 1,1 или 110%, означает, что цены возросли на 10%).

Основными элементами индекса являются:

1. Собственно индекс: индивидуальный (принято обозначать i) или сводный (I),

2. Соизмерители (веса) - в качестве соизмерителей могут выступать признаки, имеющие объемное (количественное) или качественное содержание.

3. Индексируемая величина - это значение признака статистической совокупности, изменение которого является объектом изучения. Например, при изучении изменении цен индексируемой величиной является цена единицы товара р, при изучении изменения физического объема товарной массы в качестве индексируемой величины выступают данные о количестве товаров в натуральных измерителях q.

Основными элементами индивидуального индекса являются:

1. 
   собственно индекс
   

индивидуальный индекс физического объема продукции

индивидуальный индекс цен

2. 
   индексируемая величина (для 1-го индекса будет количество товара в натуральном измерении q, для 2-го индекса - цена единицы товара р). Знак внизу справа означает период: 0 - базисный, 1 - отчетный.
   

При построении сводных индексов, отражающих влияние объемного (количественного) показателя на изменение сложного общественного явления.

Основными элементами индекса являются:

1. 
   Собственно индекс
   

индекс физического объема продукции

2. 
   Индексируемые величины q₁ и q₀
   
3. 
   Соизмерители - в качестве соизмерителей выступают неизменные цены базисного периода р₀.
   

При построении сводного индекса, отражающего влияние качественного показателя на изменение сложного общественного явления, основными элементами индекса являются:

1. Собственно индекс

индекс цен

2. 
   Индексируемые величины р₁ и р_0.
   
3. 
   Веса - в качестве которых выступают данные об объемах продукции в текущем (отчетном) периоде q₁.
   

Вопрос 2.

В статистике индексы классифицируются по ряду признаков:

1. 
   по степени охвата явления
   
2. 
   по базе сравнения
   
3. 
   по форме построения
   
4. 
   по составу явления
   
5. 
   по содержанию индексируемых величин.
   

1. По степени охвата явления индексы подразделяются на:

1. 
   индивидуальные - они характеризуют изменение отдельных единиц изучаемой совокупности (i_q, i_р)
   
2. 
   сводные - это сложные индексы и они могут быть:
   

а) общими - выражают обобщающие результаты совместного изменения всех единиц, образующих совокупность.

б) групповыми (субиндексы) - охватывают только часть (группу) единиц в изучаемой совокупности.

Примером сложного индекса может служить индекс стоимости продукции, который характеризует изменение стоимости продукции в отчетном периоде по сравнению с базисным за счет изменения q и р: .

2. 
   По базе сравнения различают:
   

1. Динамические индексы - используются для характеристики темпов изменений общественных явлений в динамике. Эти индексы в свою очередь подразделяются на базисные и цепные.

Базисными называют индексы, при исчислении которых данные всех периодов сравниваются с одним периодом, взятым за базу, обычно с начальным периодом.

Цепными называют индексы, при исчислении которых данные каждого периода сравниваются с данными предшествующего периодов. В цепных индексах база переменная.

Базисные и цепные индексы могут быть индивидуальными и общими. Индивидуальные базисные и цепные индексы представляют собой разновидность базисных и цепных относительных величин динамики - и способы их расчета поэтому тождественны. Вычисление общих (базисных и цепных индексов) имеет свои особенности. Различают общие (базисные и цепные) индексы с постоянными и переменными весами. При вычислениииндексов с постоянными весами в качестве весов для всего ряда принимаются соизмерители какого-либо одного периода.

При исчислении индексов с переменными весами в качестве весов каждый раз принимаются соизмерители другого периода.
2. Территориальные(пространственные) индексы. Индексы могут использоваться для различных экономических сравнений не только в динамике, но и в территориальном разрезе за один и тот же период (например, сравнение районов по объему производимой продукции). В таких случаях прибегают к построению так называемых территориальных индексов.


Вопрос 3.

Взаимосвязь между индексами:

1. 
   Произведение общих цепных индексов дает базисный индекс последнего периода. Пусть мы имеем 3 периода 1991, 1992, 1993.
   

.

2. 
   Поскольку величина объема продукции равна произведению количества продукции на цену, то индекс физического объема (I_q), умноженный на индекс цен (I_p) дает индекс товарооборота в фактических ценах (I_qp):
   

.

ТЕМА 9. РЯДЫ ДИНАМИКИ И ИХ АНАЛИЗ.
1. Понятие о динамических рядах. Виды рядов динамики

2. Показатели анализа ряда динамики

3. Аналитическое выравнивание динамических рядов

Вопрос 1.

Известно, что социально-экономические явления находятся в постоянном развитии во времени. Изучение процесса развития этих явлений - одна из основных задач статистики, которая решается путем построения и анализа рядов динамики.

Динамика означает изменение процессов во времени, поэтому ряд статистических показателей, характеризующий изменение общественных явлений во времени называется динамическим рядом.

Показатели, из которых состоит динамический ряд называются уровнями динамического ряда и обозначаются - У, а период времени, за который они представлены - t.

В теории статистики различают следующие виды динамических рядов:

1. 
   Моментные ряды динамики. Моментным называется ряд, уровни которого характеризуют размеры социально-экономических явлений по состоянию на определенную дату или определенный момент времени.
   
2. 
   Периодические (интервальные) ряды динамики. Периодический ряд - это такой ряд, уровни которого характеризуют размеры общественно-экономических явлений за определенный период (интервал) времени.
   

Ряды динамики формируются в результате сводки и обработки материалов периодического наблюдения. Повторяющиеся по временным периодам значения показателей в ходе статистической сводки систематизируются в хронологической последовательности. При этом каждый ряд динамики охватывает отдельные периоды, в которых могут происходить изменения, приводящие к несопоставимости отчетных данных с данными других периодов. Поэтому для анализа ряда динамики необходимо приведение всех составляющих его элементов к сопоставимому виду.
Вопрос 2.

Для количественной оценки динамики социально-экономических явлений применяется система показателей ряда динамики, которая может быть представлена следующей группой показателей:

1. Абсолютный прирост

2. Темп роста

3. Темп прироста

4. Значение 1% прироста.

В основе расчета показателей рядов динамики лежит сравнение его уровней. В зависимости от применяемого способа сопоставления (базисный или цепной) показатели динамики могут вычисляться на постоянной и переменной базах сравнения.

Для расчета показателей на постоянной базе (базисный способ расчета) каждый уровень ряда сравнивается с одним и тем же базисным уровнем. Исчисляемые при этом показатели называются базисными.

Для расчета показателей на переменной базе (цепной способ расчета) каждый последующий уровень ряда сравнивается с предыдущим. И показатели называются цепными.

Важнейшим статистическим показателем является абсолютный прирост, который показывает абсолютную скорость роста или снижения сравниваемых уровней, и рассчитывается как разность между этими уровнями (между последующим и предыдущим уровнем, принятым за базу сравнения). Измеряется в тех же единицах, что и исходная информация.

А = Y₁ – Y₀,

где Y₁ – значение отчетного уровня ряда динамики;

Y₀ – значение базисного уровня ряда динамики.

Пусть мы имеем следующий ряд динамики производства продукции в 2006-2009 г.г.

Год (t)	2006	2007	2008	2009
Уровень производства продукции, тыс. руб. (Y)	12,3	14,1	12,6	17,8

На основании данного ряда динамики рассчитаем базисные (приняв за базу сравнения 2006 год) и цепные абсолютные приросты:

Базисные: А^07/06=Y₀₇-Y₀₆; А^08/06= Y₀₈-Y₀₆; А^09/06=Y₀₉-Y₀₆

Цепные: А^07/06=Y₀₇-Y₀₆; А^08/07= Y₀₈-Y₀₇; А^09/08=Y₀₉-Y₀₈

Между цепными и базисными абсолютными приростами имеется следующая взаимосвязь: сумма цепных абсолютных приростов равна базисному абсолютному приросту последнего периода ряда динамики:

А^09/06=Y₀₉-Y₀₆=A^07/06+A^08/07+A^09/08.

Темп (коэффициент) роста показывает относительную скорость роста уровня ряда динамики и представляет собой отношение каждого последующего уровня к предыдущему, принятому за базу сравнения. Темп роста измеряется в %, а коэффициент роста - в долях.

, .

Между цепными и базисными темпами роста имеется взаимосвязь:

1. 
   Произведение последовательных цепных темпов роста равно базисному темпу роста последнего периода:
   

;

2. 
   Частное от деления последующего базисного темпа роста на предыдущий равно соответствующему цепному темпу роста: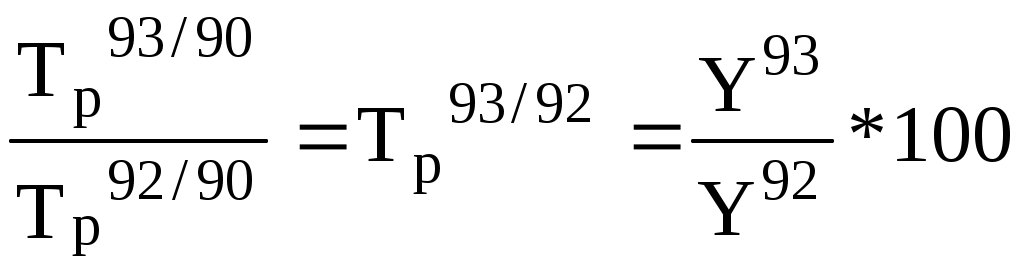
   

.

Темп (коэффициент) прироста показывает на сколько процентов изменился сравниваемый уровень с уровнем, принятым за базу сравнения:

, .

Между темпом (коэффициентом) прироста и темпом (коэффициентом) роста существует следующая взаимосвязь:

Т_пр=Т_р-100, К_пр=К_р-1.

Значение 1 % прироста определяется отношением абсолютного прироста к темпу прироста, и показывает сколько единиц в абсолютном выражении приходится на 1% прироста для данного ряда динамики. Расчет этого показателя целесообразен для цепного способа, для базисного способа он не имеет смысла (будет постоянной величиной).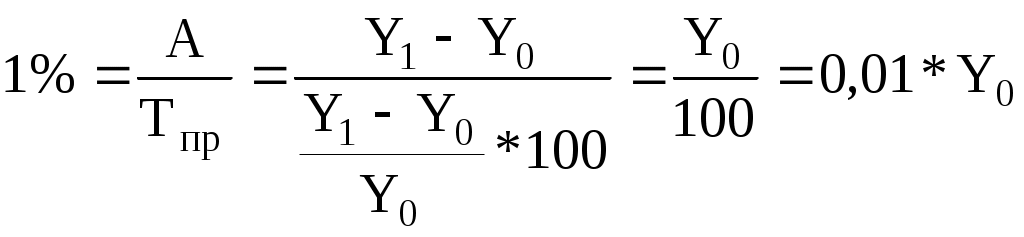

.
Расчет средних показателейряда динамики.

Для получения обобщающих показателей динамики социально-экономических явлений определяются средние величины ряда динамики:

1. 
   Средний уровень ряда динамики характеризует типическую величину абсолютных уровней.
   

В интервальных рядах динамики средний уровень определяется по формуле средней арифметической:

• 
  простой ;
  
• 
  взвешенной ,
  

где - сумма уровней; n – число уровней.

Для моментного ряда средний уровень определяется с помощью средней хронологической: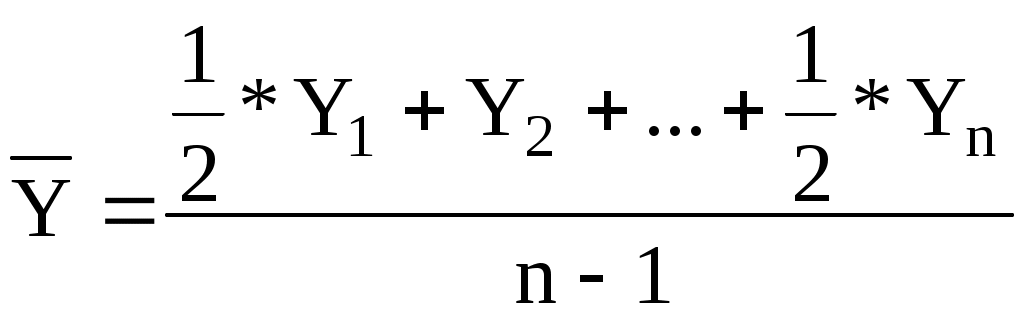

, где n – число уровней.

2. 
   Средний абсолютный прирост представляет собой обобщенную характеристику индивидуальных абсолютных приростов ряда динамики. При цепном способе для определения среднего абсолютного прироста сумма цепных абсолютных приростов делится на их число:
   

.

При базисном способе расчета чтобы определить средний абсолютный прирост, для этого определяется разность между конечным У_n и базисным У₀ уровнями изучаемого периода, которая делится на m-1 субпериодов:

.

3. 
   Средний темп роста - обобщающая характеристика индивидуальных темпов роста ряда динамики. Для определения среднего темпа роста цепным способом применяется следующая формула:
   

*100,

где К_р1, К_р2, ..., К_рn - индивидуальные (цепные) коэффициенты роста;

n - число индивидуальных темпов роста

Для базисного способа средний темп роста будет определяться по формуле:

.

4. 
   Средний темп прироста можно определить по формуле: .
   

5. 
   Среднее значение 1 % прироста определяется только для цепного способа по формуле:
   

.

Эти показатели динамики находят практическое применение во всех расчетах, где требуется изучение изменения социально-экономических явлений во времени.
Вопрос 3.

Важным направлением в исследовании закономерностей динамики социально-экономических процессов является изучение общей тенденции развития (тренда). На практике наиболее распространенными методами статистического изучения тренда являются: способ укрупнение интервалов (периодов), способ сглаживания скользящей средней, выравнивание ряда по среднегодовому абсолютному приросту, выравнивание ряда по среднегодовому темпу роста, аналитическое выравнивание при помощи способа наименьших квадратов.

1. 
   Способ укрупнения интервалов применяется для выявления тренда в рядах динамики колеблющихся уровней, затушевывающих основную тенденцию развития. Сущность этого приема состоит в том, что данные или уровни за отдельные отрезки времени суммируются в ряды более продолжительных периодов (месячные в квартальные, квартальные в годовые), определяется средний уровень для полученного укрупненного периода. В результате после укрупнения периодов очевидной становится тенденция развития явления.
   
2. 
   Способ скользящей средней. Скользящая средняя - это подвижная динамическая средняя, которая подсчитывается по динамическому ряду при последовательном передвижении на 1 год или на 1 интервал. Правильно исчисленная скользящая средняя устраняет в ряду динамики случайные колебания и дает возможность точнее выявить тенденцию в развитии, чем укрупненные интервалы.
   

3. 
   Еще более точным способом является выравнивание по среднегодовому абсолютному приросту, которое рассчитывается по формуле:
   

,

где - выровненное значение;

Y₀ - начальный уровень ряда;

- средний базисный абсолютный прирост, который вычисляется по формуле:

,

где n - число лет;

t - порядковый номер года, в котором были приросты.

4. Выравнивание ряда по среднегодовому коэффициенту роста имеет следующий вид: ,

где - выровненное значение;

Y₀ - начальный уровень ряда

- среднегодовой базисный коэффициент роста, определяемый по формуле:

,

n – число лет;

t - порядковый номер года.

5. 
   Способом аналитического выравнивания можно получить обобщенную статистическую оценку тренда. Наиболее совершенным является способ наименьших квадратов, которому соответствует условие, что сумма квадратов отклонений фактического и теоретического уровней будет минимальной. Простейшим приемом является выравнивание ряда динамики по прямой: ,
   

где а - свободный член;

b - коэффициент приращения;

t - период времени.

Способ наименьших квадратов дает систему двух нормальных уравнений для вычисления параметров функции:

,

,

где Y – исходные уровни ряда;

n – число членов ряда;

t – время.

Для упрощения вычислений показателям времени t придают такие значения, чтобы их сумма была равна нулю ( ). При этом используют следующие формулы:

• 
  если ряд содержит четное число членов
  

• 
  если ряд содержит нечетное число членов ,
  

где k – порядковый номер года;

n – число лет в периоде.

При система уравнений будет иметь следующий вид:

,

.

Исходя из полученной системы уравнений найдем параметры уравнения прямой:

,

.