ОСУ 8 ЛР. лр 8 ОргСУ Перова К. ДИССМ11. Лабораторная работа 8 методы подтверждения адекватности проведённых экспериментальных исследований
 Скачать 0.54 Mb. Скачать 0.54 Mb.
|
Астрахань, 2020 Лабораторная работа №8 Методы подтверждения адекватности проведённых экспериментальных исследований Цель работы: получить навыки в вопросах проверки адекватности проведённых исследований (экспериментов). Задание: На основе изучения материалов провести оценку адекватности (первая процедура проверки). Рассчитать абсолютную ошибку. Рассчитать коэффициент вариации. Рассчитать относительную ошибку. Провести вторую процедуру оценки адекватности: проверить остатки по критерию Пирсона, оценить однородность дисперсии остатков. Проверить адекватность по критерию Фишера. Корректировка значений затухания, измеренных ПКП «ONEGA» по результатам натурных испытаний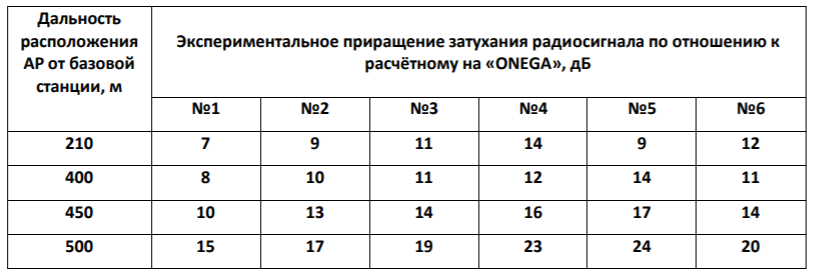 Математическое ожидание Mx случайной величины равно: 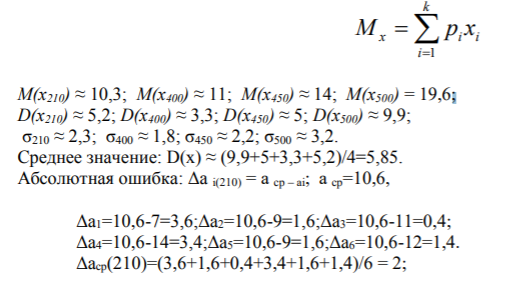 Относительная ошибка результата измерений для удалённости абонентской радиостанции в 200 метров: 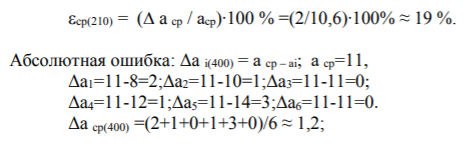 Относительная ошибка результата измерений для удаленности АР в 400м: ε ср(400) = (Δаср / acp)∙100 %=(1,2/11)∙100% ≈ 11 %.  Относительная ошибка результата измерений для удаленности АР в 500м:  В таблице приведены сравнение модельных и полученных экспериментально приращений затухания радиосигнала за счёт наличия древесных насаждений, не обозначенных на цифровых картах. 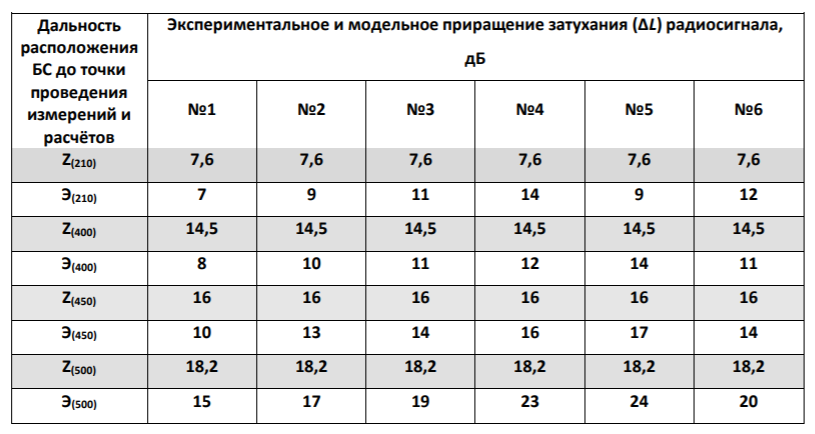 Оценка результатов эксперимента Доверительные интервалы для генеральной средней и дисперсии нормального случайного признака Осуществим оценку адекватности методики косвенным методом, путем анализа остатков, т. е. разностей между истинными значениями параметра отношения сигнала к помехе и предсказанными выше описанной методикой. В случае, когда модель адекватна, остатки имеют нормальное распределение. Произведено по 6 измерений уровня затухания сигнала за счёт древесных насаждений и зданий на исследуемом участке ССС на расстоянии 200, 300, 400, 500 метров от БС до АР. В соответствии с таблицей 6 составлена таблица отклонений от среднего значения уровня сигнала (табл. 6) Отклонение от среднего значения уровня затухания сигнала
Вычислим выборочную среднюю и дисперсию случайной величины ΔU. 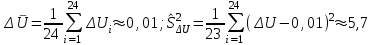 Далее из таблицы значения t-критерия Стьюдента при α = 0,95 (или уровне значимости 0,05) и числе степеней свободы l = n-1 = 2 находим ta = 2,0687 . Вычисляем предельное отклонение: 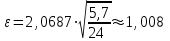 Находим доверительный интервал для генеральной средней: 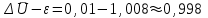 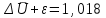 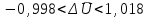 Теперь из таблицы значений критических точек распределения при 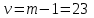 и и 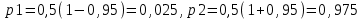 находим: находим: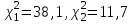  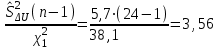 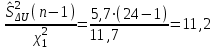 Доверительный интервал: 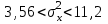 Расчёт коэффициента детерминации Для проведения предварительного анализа достоверности методики необходимо рассчитать ко- эффициент детерминации: R2. Квадрат множественного коэффициента корреляции называется множественным коэффициен- том детерминации. Он показывает, какая доля дисперсии результативного признака объясняется вли- янием независимых переменных. где ESS TSS RSS , n R 2 ТSS (%); ESS где ESS yi i1 i n y2 , Explained Sum of Squares – «объяснённая» регрессией сумма квадратов; i TSS yi i1 n y2 , - Total Sum of Squares – полная сумма квадратов; i RSS yi i1 y2 - Residual Sum of Squares – остаточная сумма квадратов. yi - экспериментальные значения (табл. 6); y- модельное значение, вычисленное с помощью разработанной методики расчёта; y - среднее значение всех проведённых измерений. При этом для первого эксперимента: RSS=45,34; TSS=33,14; ESS=74,16. R2 (200) 74%. При этом для второго эксперимента: yi 7,8 , yi 15,5 , y 10,3 . y 12. RSS=72,4; TSS=21,6; ESS=91,3. R2 (300) 22% . При этом для третьего эксперимента: RSS=24; TSS=30; ESS=54. R2 (400) 56% . yi 16 , y 14 . При этом для четвёртого эксперимента: RSS=13,86; TSS=63,47; ESS=79,11. R2 (500) 79% . yi 19,3 , y 20,5 . R2 R2 (210) R2 (400) R2 (450) R2 (500) 4 58 Следовательно, это показывает, что ≈ 60 % изменений в расчётном значении затухания сигнала сотовой связи зависит от новой методики расчёта дополнительного затухания в листве и зданиях, необозначенных на цифровых картах. Однофакторный дисперсионный анализ Полученную с помощью факторного эксперимента модель (методику) необходимо проверить на адекватность. Это осуществляется с помощью критерия Фишера[9, 10]. Анализ результатов будет основан на сопоставлении двух оценок неизвестной дисперсии 2 . Если обе оценки близки, то гипотезу H 0 (методику расчёта затухания) следует принять. Если же оценки существенно отличаются, то гипотезу методики расчёта затухания в листве необозначенных на цифровых картах древесных насаждений следует отвергнуть. Сведём данные наблюдений по таблице 4 в таблицу 9: Данные наблюдений процентной корректировки затухания сигнала
Сначала для каждой строки вычислим среднее: 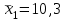 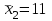 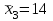 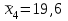 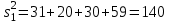 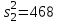 При n=6, m=4, 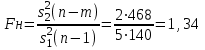 Для F-критерия имеются специальные таблицы (таблица 10) распределения Фишера, рассчитанные для различного числа степеней свободы и доверительных вероятностей P (уровней значимости). где в соответствии со степенями свободы 1 n 1 и m, n 2 где n – число измерений в выборке, m – количество выборок. По таблице распределения Фишера для v1 = 5, v2 = 19,3. Таким образом, с помощью F-критерия проверяется лишь тот факт, что дисперсия адекватности не отличается значимо от дисперсии воспроизводимости, то есть ошибка модели (методики) и ошибка, связанная с точностью эксперимента, на основе которого построена методика, адекватны. |

