Математическое планирование. Отчет по последней работе. Отчет по работе Обработка результетов эксперимента для двухфакторного плана пфэ

• Название: Отчет по работе Обработка результетов эксперимента для двухфакторного плана пфэ
• Анкор: Математическое планирование
• Дата: 14.04.2022
• Размер: 164.7 Kb.
• Имя файла: Отчет по последней работе.docx
• Тип: Отчет; #474423

Отчет по работе: «Обработка результетов эксперимента для двухфакторного плана ПФЭ»

Выполнили (Булсунаева Оксана, Астраханцева Анастасия)

Планирование эксперимента – это процедура выбора числа и условий проведения опытов, необходимых и достаточных для решения поставленной задачи с требуемой точностью.
Ход работы планирования эксперимента

Обычно план эксперимента задается в виде матрицы планирования, каждая строка которой определяет условие опыта, а каждый столбец – значения контролируемых и управляемых параметров в исследуемом процессе, т.е. значения факторов, соответствующих условию опыта.



Рисунок 1 – матрица планирования эксперимента

В данной работе производился расчет плана эксперимента по заданным переменным факторам (рисунок 2):

	Вариант 1			Вариант 5
1	5,16	5,16	5,15	12,67	12,66	12,64
2	5,15	5,17	5,16	12,65	12,68	12,67
3	5,19	5,19	5,20	12,75	12,73	12,76
4	5,04	5,05	5,04	12,38	12,40	12,36
5	5,06	5,05	5,07	12,43	12,39	12,44
6	5,12	5,10	5,11	12,56	12,51	12,53
7	4,95	4,96	4,96	12,15	12,18	12,17
8	5,13	5,12	5,13	12,58	12,58	12,58
9	5,24	5,26	5,25	12,86	12,90	12,89

Вариант 1 – Астраханцева Анастасия; вариант 5 – Булсунаева Оксана

Рисунок 2 – Выходные параметры
При расчете коэффициентов уравнения математической модели, который был произведен в программе Excel, мы получили значения (рисунок 3), которые позволили вывести функцию отклика (формула 2,3).

Коэффициенты уравнения регрессии	Вариант 1	Вариант 5
В0	5,06926	12,44074
В1	0,06611	0,16
В2	-0,0294	-0,07333
В12	0,06417	0,156667
В11	0	0
В22	0,06944	0,172222

Вариант 1 – Астраханцева Анастасия; вариант 5 – Булсунаева Оксана

Рисунок 3 – коэффициенты математической модели
у = b₀ + b₁*х₁ + b₂*х₂ + b₁₂*х₁*х₂+b₂₂*(x₂)² (1)

Функция отклика Астраханцевой Анастасии:

y=5,069+0,066-0,029*х₂+0,064*х₁*х₂+0,069*(x₂)²

Функция отклика Булсунаевой Оксаны:

y=12,44+0,16-0,073*х₂+0.064*х₁*х₂+0,069*(x₂)²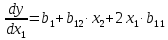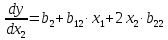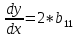






Вывод: т.к. значения коэффициентов в двух вариантах равны = 0, следовательно, невозможно найти точки максимума и минимума данной функции.

Найдем наименьшее и наибольшее значения функции:

Находим производную данной функции 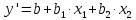и приравняем производную нулю ( )
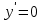Функция Булсунаевой Оксаны

y=12,44+0.016·x₁-0.073·x₂

Первая производная функции

y'=0,087

Приравниваем ее к нулю:

0,087≠0 ⟶ глобальных экстремумов нет
Функция Астраханцева Анастасия

y=5.069+0.066·x₁-0.029·x₂

Первая производная функции

y'=0,037

Приравниваем ее к нулю:

0,037≠0 ⟶ глобальных экстремумов нет


Необходимое условие экстремума функции одной переменной.
Уравнение f'₀(x*) = 0 - это необходимое условие экстремума функции одной переменной, т.е. в точке x* первая производная функции должна обращаться в нуль. Оно выделяет стационарные точки x_с, в которых функция не возрастает и неубывает.

Достаточное условие экстремума функции одной переменной.

Пусть f0(x) дважды дифференцируемая по x, принадлежащему множеству D. Если в точке выполняется условие:

f'0(x*)=0

f''0(x*)>0

то точка x* является точкой локального (глобального) минимума функции.

Если в точке x* выполняется условие:

f'0(x*)=0

f''0(x*)<0

То в точкаx *-локальный(глобальный)максимум.


Вывод: расчеты показали, что глобальных экстремумов обнаружено не было.