эссе. Лабораторная работа 8 Работа с двумерными массивами (1). Лабораторная работа 8 Работа с двумерными массивами
 Скачать 166.65 Kb. Скачать 166.65 Kb.
|
Лабораторная работа 8 Работа с двумерными массивами.Цель работы: изучение двумерных массивов в Python. знать - способ описания двумерного массива, способы ввода элементов двумерного массива; уметь - вводить массивы, получать списки через присваивание конкретных значений, применять функции; владеть - основными навыками создания программ обработки двумерных массивов. Матрицами называются массивы элементов, представленные в виде прямоугольных таблиц, для которых определены правила математических действий. Элементами матрицы могут являться числа, алгебраические символы или математические функции. Для работы с матрицами в Python также используются списки. Каждый элемент списка-матрицы содержит вложенный список. Таким образом, получается структура из вложенных списков, количество которых определяет количество столбцов матрицы, а число элементов внутри каждого вложенного списка указывает на количество строк в исходной матрице. 1. Создание списка Пусть даны два числа: количество строк n и количество столбцов m. Необходимо создать список размером n×m, заполненный нулями. Очевидное решение оказывается неверным: A = [ [0] *m ]*n В этом легко убедиться, если присвоить элементу A[0][0] значение 1, а потом вывести значение другого элемента A[1][0] — оно тоже будет равно 1! Дело в том, что [0] * m возвращает ccылку на список из m нулей. Но последующее повторение этого элемента создает список из n элементов, которые являются ссылкой на один и тот же список (точно так же, как выполнение операции B = A для списков не создает новый список), поэтому все строки результирующего списка на самом деле являются одной и той же строкой. Таким образом, двумерный список нельзя создавать при помощи операции повторения одной строки. Первый способ. Сначала создадим список из n элементов (для начала просто из n нулей). Затем сделаем каждый элемент списка ссылкой на другой одномерный список из m элементов: A = [0] * n for i in range(n): A[i] = [0] * m  Второй способ. Создать пустой список, потом n раз добавить в него новый элемент, являющийся списком-строкой: A = [] for i in range(n): A.append([0] * m)  2. Ввод вложенного списка (двумерного массива) Пример: n=5 A = [] for i in range(n): b = input() for i in range(len(row)): row[i] = int(row[i]) A.append(row) 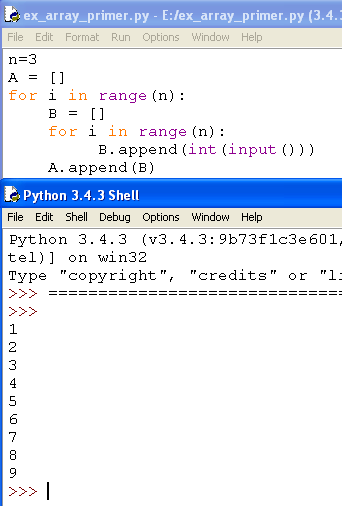 3. Вывод вложенного списка (двумерного массива) Для обработки и вывода списка как правило используется два вложенных цикла. Первый цикл по номеру строки, второй цикл по элементам внутри строки. Например, вывести двумерный числовой список на экран построчно, разделяя числа пробелами внутри одной строки, можно так: for i in range(n): for j in range(n]): print(A[i][j], end = ' ') print()   То же самое, но циклы не по индексу, а по значениям списка: for row in A: for elem in row: print(elem, end = ' ') print() 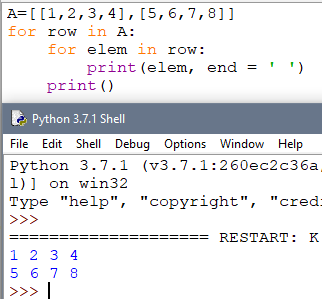 Для вывода одной строки можно воспользоваться методом join. Использовав этот метод в цикле for можно for row in A: print(' '.join(list(map(str, row)))) 4. Обработка и вывод вложенных списков Часто в задачах приходится хранить прямоугольные таблицы с данными. Такие таблицы называются матрицами или двумерными массивами. В языке программирования Питон таблицу можно представить в виде списка строк, каждый элемент которого является в свою очередь списком, например, чисел. Например, создать числовую таблицу из двух строк и трех столбцов можно так: A = [ [1, 2, 3], [4, 5, 6] ] Здесь первая строка списка A[0] является списком из чисел [1, 2, 3]. То есть A[0][0]= 1, A[0][1]= 2, A[0][2]= 3, A[1][0]=4, A[1][1]=5, A[1][2]=6. Используем два вложенных цикла для подсчета суммы всех чисел в списке: S = 0 for i in range(len(A)): for j in range(len(A[i])): S += A[i][j] Или то же самое с циклом не по индексу, а по значениям строк: S = 0 for row in A: for elem in row: S += elem   5. Пример сложной обработки массива Пусть дана квадратная матрица из n строк и n столбцов. Необходимо элементам, находящимся на главной диагонали, проходящей из левого верхнего угла в правый нижний (то есть тем элементам A[i][j], для которых i==j) присвоить значение 0, элементам, находящимся выше главной диагонали – значение 1, элементам, находящимся ниже главной диагонали – значение 2. То есть получить такой массив (пример для n==3): 0 1 1 2 0 1 2 2 0 Рассмотрим несколько способов решения этой задачи. Первый способ. Элементы, которые лежат выше главной диагонали – это элементы A[i][j], для которых i for i in range(n): for j in range(n): if i < j: A[i][j] = 0 elif i > j: A[i][j] = 2 else: A[i][j] = 1 Ниже приведён пример программы, в котором квадратная матрица 3х3 заполняется элементами со значением 9, а затем элементам, находящимся на главной диагонали, проходящей из левого верхнего угла в правый нижний (то есть тем элементам A[i][j], для которых i==j) присваивается значение 0, элементам, находящимся выше главной диагонали – значение 1, элементам, находящимся ниже главной диагонали – значение 2.  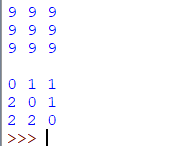 Второй способ. Данный алгоритм плох, поскольку выполняет одну или две инструкции if для обработки каждого элемента. Если мы усложним алгоритм, то мы сможем обойтись вообще без условных инструкций. Сначала заполним главную диагональ, для чего нам понадобится один цикл: for i in range(n): A[i][i] = 1 Затем заполним значением 0 все элементы выше главной диагонали, для чего нам понадобится в каждой из строк с номером i присвоить значение элементам A[i][j] для j=i+1, ..., n-1. Здесь нам понадобятся вложенные циклы: for i in range(n): for j in range(i + 1, n): A[i][j] = 0 Аналогично присваиваем значение 2 элементам A[i][j] для j=0, ..., i-1: for i in range(n): for j in range(0, i): A[i][j] = 2 Можно также внешние циклы объединить в один и получить еще одно, более компактное решение: for i in range(n): for j in range(0, i): A[i][j] = 2 A[i][i] = 1 for j in range(i + 1, n): A[i][j] = 0   Третий способ. А вот такое решение использует операцию повторения списков для построения очередной строки списка. i-я строка списка состоит из i чисел 2, затем идет одно число 1, затем идет n-i-1 число 0: for i in range(n): A[i] = [2] * i + [1] + [0] * (n - i - 1) 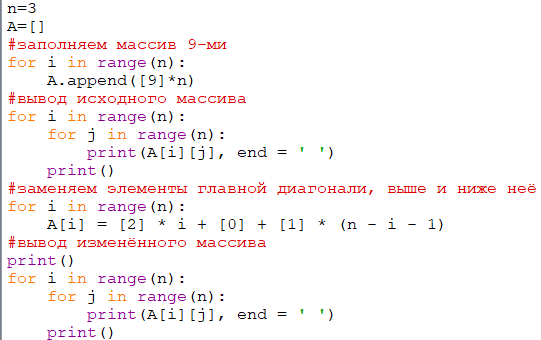  Вариант 0 1. Дан двумерный массив размером 3x3. Определить максимальное значение среди элементов третьего столбца массива; максимальное значение среди элементов второй строки массива. Вывести полученные значения. Решение:   2. Дан двумерный массив размером mxn. Сформировать новый массив заменив положительные элементы единицами, а отрицательные нулями. Вывести оба массива. Решение:   Вариант 1. 1. Вычислить сумму и число положительных элементов матрицы A[N, N], находящихся над главной диагональю. 2. Дана матрица B[N, М]. Найти в каждой строке матрицы максимальный и минимальный элементы и поменять их с первым и последним элементами строки соответственно. Вариант 2. 1. Дана целая квадратная матрица n-го порядка. Определить, является ли она магическим квадратом, т. е. такой матрицей, в которой суммы элементов во всех строках и столбцах одинаковы. 2. Дана прямоугольная матрица A[N, N]. Переставить первый и последний столбцы местами и вывести на экран. Вариант 3. 1. Определить, является ли заданная целая квадратная матрица n-го порядка симметричной (относительно главной диагонали). 2. Дана вещественная матрица размером n х m. Переставляя ее строки и столбцы, добиться того, чтобы наибольший элемент (или один из них) оказался в верхнем левом углу. Вариант 4. 1. Дана прямоугольная матрица. Найти строку с наибольшей и строку с наименьшей суммой элементов. Вывести на печать найденные строки и суммы их элементов. 2. Дана квадратная матрица A[N, N], Записать на место отрицательных элементов матрицы нули, а на место положительных — единицы. Вывести на печать нижнюю треугольную матрицу в общепринятом виде. Вариант 5. 1. Упорядочить по возрастанию элементы каждой строки матрицы размером n х m. 2. Дана действительная матрица размером n х m, все элементы которой различны. В каждой строке выбирается элемент с наименьшим значением. Если число четное, то заменяется нулем, нечетное - единицей. Вывести на экран новую матрицу. Вариант 6. 1. Дана целочисленная квадратная матрица. Найти в каждой строке наибольший элемент и в каждом столбце наименьший. Вывести на экран. 2. Дана действительная квадратная матрица порядка N (N — нечетное), все элементы которой различны. Найти наибольший элемент среди стоящих на главной и побочной диагоналях и поменять его местами с элементом, стоящим на пересечении этих диагоналей. Вариант 7. 1. Квадратная матрица, симметричная относительно главной диагонали, задана верхним треугольником в виде одномерного массива. Восстановить исходную матрицу и напечатать по строкам. 2. Для заданной квадратной матрицы сформировать одномерный массив из ее диагональных элементов. Найти след матрицы, просуммировав элементы одномерного массива. Преобразовать исходную матрицу по правилу: четные строки разделить на полученное значение, нечетные оставить без изменения. Вариант 8. 1. Задана матрица порядка n и число к. Разделить элементы k-й строки на диагональный элемент, расположенный в этой строке. 2. Задана квадратная матрица. Получить транспонированную матрицу (перевернутую относительно главной диагонали) и вывести на экран. Вариант 9. 1. Для целочисленной квадратной матрицы найти число элементов, кратных k, и наибольший из этих элементов. 2. В данной действительной квадратной матрице порядка n найти наибольший по модулю элемент. Получить квадратную матрицу порядка n — 1 путем отбрасывания из исходной матрицы строки и столбца, на пересечении которых расположен элемент с найденным значением. Вариант 10. 1. Найти максимальный среди всех элементов тех строк заданной матрицы, которые упорядочены (либо по возрастанию, либо по убыванию). 2. Расположить столбцы матрицы D[M, N] в порядке возрастания элементов k-й строки (1 <= k <= М). Вариант 11. 1. В данной действительной квадратной матрице порядка п найти сумму элементов строки, в которой расположен элемент с наименьшим значением. Предполагается, что такой элемент единственный. 2. Среди столбцов заданной целочисленной матрицы, содержащих только такие элементы, которые по модулю не больше 10, найти столбец с минимальным произведением элементов и поменять местами с соседним. Вариант 12. 1. Для заданной квадратной матрицы найти такие k, что k-я строка матрицы совпадает с k-м столбцом. 2. Дана действительная матрица размером n х m. Требуется преобразовать матрицу: поэлементно вычесть последнюю строку из всех строк, кроме последней. Вариант 13. 1. Определить наименьший элемент каждой четной строки матрицы А[М, N]. 2. Найти наибольший и наименьший элементы прямоугольной матрицы и поменять их местами. Вариант 14. 1. Задана квадратная матрица. Переставить строку с максимальным элементом на главной диагонали со строкой с заданным номером m. 2. Составить программу, которая заполняет квадратную матрицу порядка п натуральными числами 1, 2, 3, ..., n2, записывая их в нее «по спирали». Например, для п = 5 получаем следующую матрицу: 1 2 3 4 5 16 17 18 19 6 15 24 25 20 7 14 23 22 21 8 14 12 11 10 9 Вариант 15. 1. Определить номера строк матрицы R[M, N], хотя бы один элемент которых равен с, и элементы этих строк умножить на d. 2. Среди тех строк целочисленной матрицы, которые содержат только нечетные элементы, найти строку с максимальной суммой модулей элементов. Список литературы 1. https://pythontutor.ru/lessons/2d_arrays/ 2. http://labs.org.ru/python-8/ 3. http://progras.ru/31-dvumernye-spiski-massivy-matricy-v-python/ |
