Лабораторная работа №8
ВЗАИМОДЕЙСТВИЕ - ЭЛЕКТРОНОВ С ВЕЩЕСТВОМ
Цель работы:
Изучить механизмы взаимодействия электронов с веществом;
Определить граничную энергию - спектра методом поглощения.
Взаимодействие электронов с веществом
Электроны, проходящие через вещество, испытывают упругое и неупругое рассеяние, а также излучают фотоны при взаимодействии с ядрами и электронами окружающей среды. В результате, частицы теряют свою энергию и отклоняются от первоначального направления. Поглощение электронов обусловлено потерями энергии на ионизацию и возбуждение атомов (ионизационные потери), а также при высоких энергиях на тормозное излучение (радиационные потери).
Удельные потери энергии на ионизацию для моноэнергетических электронов описываются формулой Бете-Блоха:

где m - масса покоя электрона; I-средний ионизационный потенциал атомов вещества; = v/c; v – скорость электрона, влетающего в мишень; N - число атомов в 1 см3 вещества; Z - атомный номер вещества; Е - релятивистская кинетическая энергия электрона; -поправка на эффект плотности.


Рис.1. Зависимость ионизационных потерь электрона в свинце и алюминии от энергии
Графически зависимость ионизационных потерь (dE/dx) от энергии падающего электрона показана на Рис.1
На первом участке Рис.1 релятивистские эффекты несущественны и зависимость ионизационных потерь от энергии определяется в основном общим множителем, стоящим перед логарифмом в формуле (1), т.е. они обратно пропорциональны квадрату скорости частицы.
На втором участке становятся важны релятивистские эффекты, связанные, в первую очередь, с релятивистским изменением электромагнитного поля частицы.
Анализ кулоновской силы, действующей на атомный электрон со стороны движущегося электрона, показывает, что действие продольной относительно скорости электрона составляющей кулоновской силы обращается в ноль, вследствие изменения ее знака в процессе взаимодействия. Поперечная же составляющая, сохраняя свое направление на всей траектории электрона, приводит к ионизации атома (см. Векторную схему на Рис.2).

Рис.2. Диаграмма кулоновских сил, действующих со стороны падающего электрона епад. на электрон среды еа в двух произвольных точках (1) и (2) , симметрично расположенных относительно перпендикуляра, опущенного из точки расположения электрона атома на траекторию падающего электрона F = e2 / 2
Известно, что при малых скоростях частицы ее электромагнитное поле сферически симметрично. При релятивистских скоростях, оставаясь симметричным в системе покоя частицы, электромагнитное поле в лабораторной системе вытягивается в поперечной плоскости, согласно преобразованиям Лорентца. При скорости частицы, приближающейся к скорости света, ее электромагнитное поле стремиться к поперечному полю фотона. В результате увеличивается эффективная область вещества, с атомами которой взаимодействует электрон. Это приводит к логарифмическому росту (-dE/dx).
В области III – ограничение логарифмического роста связано с поляризацией атомов среды вблизи траектории частицы, которая приводит к экранировке (уменьшению) электромагнитного поля, действующего на электроны далеких атомов. Этот эффект пропорционален плотности атомов в веществе, поэтому он назван эффектом плотности. В формуле (1) эффект плотности описывается членом .
При рассмотрении элементарного процесса взаимодействия двух электронов в формуле Бете-Блоха масса электрона должна быть заменена приведенной массой, в отличие от формулы для ионизационных потерь тяжелых заряженных частиц. Необходимо также учитывать квантовомеханический эффект обмена, обусловленный неразличимостью микрочастиц.
Электрон среды, выбитый из атома в процессе ионизации, может иметь энергию, достаточную в свою очередь для ионизации атомов среды. Такие электроны называются δ-электронами и играют существенную роль в процессе регистрации заряженных частиц.
Радиационные потери энергии электрона происходят за счет излучения электромагнитных волн при торможении электронов в кулоновском поле ядер и электронов среды. Вероятность тормозного излучения, а, следовательно, и радиационные потери энергии определяются, в первую очередь, величиной ускорения частицы при торможении:
 

|a|2
Z2/m2e
где Z – заряд атомов среды, me – масса электрона. Вследствие обратной пропорциональности вероятности тормозного излучения квадрату массы излучающих частиц, интенсивность радиационных потерь электронов и тяжелых заряженных частиц при равных энергиях различается в 106 раз.
Полное рассмотрение радиационных потерь для электронов в рамках квантовой электродинамики было проведено Бете и Гайтлером. Показано, что с логарифмической точностью удельные радиационные потери энергии при относительно невысоких энергиях можно представить формулой:
 , (2) , (2)
где А - постоянная, зависящая от плотности атомов в среде и заряда среды.
Из формулы (2) также следует, что энергия частицы в результате радиационных потерь уменьшается экспоненциально
  , (3) , (3)
где Lрaд – радиационная длина, т.е. длина, на которой энергия электрона вследствие излучения уменьшается в е раз. Радиационные длины для различных частиц приведены в справочниках.
Сравнивая зависимость от энергии ионизационных и радиационных потерь энергии (см. Формулы (1) и (2) ) видно, что если при низких энергиях заряженной частицы основной вклад в потери энергии вносит ионизационный механизм, то с увеличением энергии всегда основным механизмом потери энергии становится излучение. Энергия, при которой потери энергии на излучение и ионизацию сравниваются, называется критической Екр. Для свинца, например, значение критической энергии составляет Екр = 6.9 МэВ, а для алюминия - Екр = 47 МэВ. Для алюминия при энергии электронов порядка 10МэВ потери энергии на излучение составляют приблизительно 16% ионизационных потерь энергии при столкновения с атомами среды. Следовательно, при энергии электрона порядка или ниже нескольких мегаэлектронвольт можно с высокой степенью точности пренебречь потерями энергии на излучение.
Теряя энергию при взаимодействии с атомами среды, электроны замедляются до полной остановки. Величиной, характеризующей глубину проникновения электронов в вещество, является длина пробега электронов в веществе. Вследствие вероятностного характера потерь энергии электроном при взаимодействии с атомами среды, можно говорить только о средних удельных потерях электронов в веществе и, соответственно, о средней длине пробега  , которая определяется как , которая определяется как
 , (4) , (4)
где Е0 – начальная энергия влетающего в мишень электрона.

Рис.3 Кривые пропускания моноэнергетических электронов
Экспериментально длину пробега определяют, измеряя кривую пропускания электронов в мишени, т.е. зависимость числа прошедших через мишень (зарегистрированных детектором) электронов от толщины мишени. Граница кривой пропускания с учетом фона и определяет длину пробега электронов в веществе.
Однозначное определение границы кривой поглощения на эксперименте затруднительно, поэтому обычно экстраполируют линейную часть функции к нулю. На Рис.3 приведены кривые пропускания моноэнергетических электронов в алюминии.
В отличии от монохроматических электронов, получаемых в ускорителях, электроны -спектра имеют непрерывный спектр энергии. В результате усреднения по спектру энергий влетающих в мишень частиц, вид кривой пропускания электронов в веществе существенно изменяется. Для не слишком толстых поглотителей экспериментальная кривая пропускания электронов β-распада хорошо описывается экспоненциальной функцией
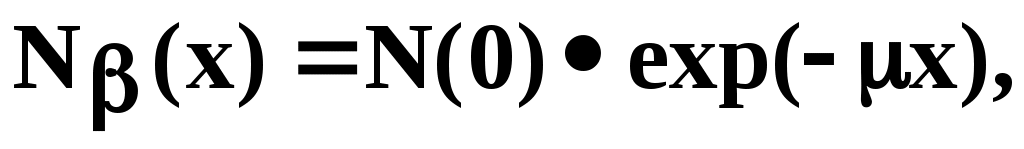
где - линейный коэффициент ослабления пучка электронов в поглотителе; x – толщина поглотителя; N(0) и N(x) – число электронов, влетающих в мишень и вылетающих из мишени, соответственно.
В эксперименте в качестве кривой пропускания удобнее рассматривать величину  , которая изменяется от 1 до 0. , которая изменяется от 1 до 0.

Рис.4. Кривая пропускания электронов: а – в обычном масштабе, б – в полулогарифмическом масштабе
Кривая пропускания (см. Рис.4а) при больших толщинах поглотителя асимптотически выходит на линию фона, что затрудняет экспериментальное определение точки пересечения кривой с уровнем фона и, следовательно, определение действительного пробега электронов в веществе  . Для уменьшения ошибки кривую пропускания удобнее строить в полулогарифмическом масштабе (см. Рис.4б). Вследствие отклонения кривой пропускания от экспоненциального закона в начале и в конце кривой, для определения . Для уменьшения ошибки кривую пропускания удобнее строить в полулогарифмическом масштабе (см. Рис.4б). Вследствие отклонения кривой пропускания от экспоненциального закона в начале и в конце кривой, для определения 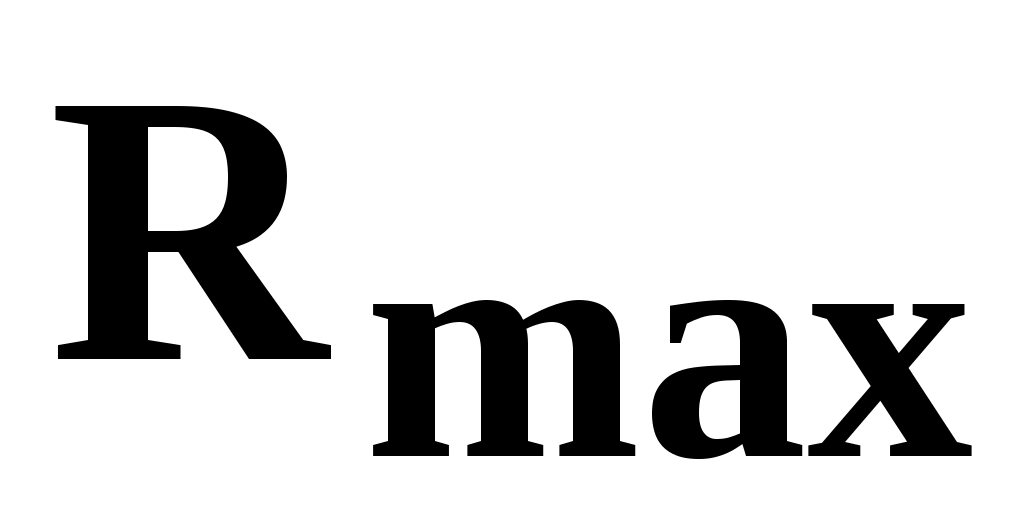 следует использовать среднюю часть измеренной кривой пропускания. следует использовать среднюю часть измеренной кривой пропускания.
Максимальный пробег  , определяемый пересечением функции ln(T(x)) с линией фона, соответствует длине пробега электронов с максимальной (граничной) энергией в - спектре. , определяемый пересечением функции ln(T(x)) с линией фона, соответствует длине пробега электронов с максимальной (граничной) энергией в - спектре.

Рис.5. Связь максимальной энергии - спектра и пробега электронов - распада в алюминии
Следовательно, определив  , мы можем найти граничную энергию для данного - спектра. Связь между , мы можем найти граничную энергию для данного - спектра. Связь между  и граничной (максимальной) энергией приведена на Рис.5 и граничной (максимальной) энергией приведена на Рис.5
2.Экспериментальная часть
В предлагаемом для эксперимента Sr-Y источнике происходит два последовательных - распада, причем граничные энергии этих распадов сильно отличаются:  << << (см. экспериментальный спектр без поглотителя). Как следствие, кривая пропускания электронов описывается суммой двух экспонент с различными коэффициентами ослабления (см. экспериментальный спектр без поглотителя). Как следствие, кривая пропускания электронов описывается суммой двух экспонент с различными коэффициентами ослабления  и и  , соответствующими двум разным компонентам - спектра: , соответствующими двум разным компонентам - спектра:
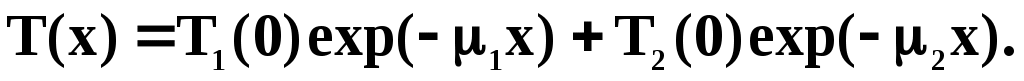 ( 5) ( 5)
Вследствие сильного различия максимальных энергий для двух последовательных - распадов, существенно различаются и значения соответствующих коэффициентов ослабления  и и  : :  >> >>  при при  << << . Как следствие, при толщинах поглотителя, для которых x >>1/ . Как следствие, при толщинах поглотителя, для которых x >>1/ , вкладом первой компоненты в (5) в кривую поглощения можно пренебречь. В этом случае можно считать, что , вкладом первой компоненты в (5) в кривую поглощения можно пренебречь. В этом случае можно считать, что
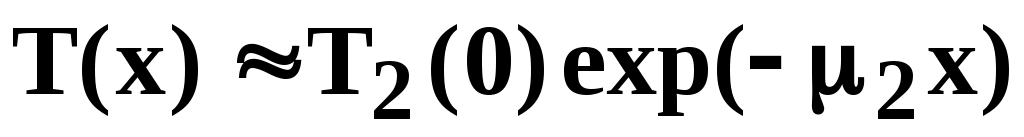 при x >> 1 / при x >> 1 /  . .
Для указанных толщин поглотителeй логарифмическая кривая пропускания имеет вид прямой с углом наклона, определяемым коэффициентом ослабления  . .
При малой толщине поглотителя ( x << x <<  x < 1) обе экспоненты вносят вклад в кривую пропучкания и, как следствие, график ln{Т(x)} существенно отклоняется от прямой. x < 1) обе экспоненты вносят вклад в кривую пропучкания и, как следствие, график ln{Т(x)} существенно отклоняется от прямой.

Рис.6. Схема распада Sr -Y источника
Порядок проведения эксперимента
Внимание! Перед началом работы убедитесь в заземлении блока сцинтилляционного детектора.
Включить компьютер, а затем блок спектрометра. Открыть программу «Спектр». После регистрации войти в программу «Спектр» и задать режимы работы спектрометра: рабочее напряжение U, коэффициент усиления К, значение нижнего уровня дискриминации ДНУ и значение верхнего уровня дискриминации ДВУ, установить время набора спектра Т = 100сек. Установить источник β-электронов Sr-Y.
Снять спектр Sr -Y источника без поглотителя и определить интегральное число импульсов (электронов), зарегистрированных детектором –N(0).
Аналогично провести измерение интегрального числа электронов N(xI), последовательно помещая поглотители различной толщины xi между источником и детектором. Использовать все имеющиеся поглотители.
4.Измерить фон в отсутствии источника.
Обработка результатов
Задание 1.
Рассчитать кривую пропуская электронов в веществе, т.е. найти значения
 , ,
где  - число электронов прошедших через поглотитель толщиной xI (i – предполагает перечисление всех поглотителей). - число электронов прошедших через поглотитель толщиной xI (i – предполагает перечисление всех поглотителей).
Задание 2. Измерить фон.
Задание 3.
Зайти в программу «MathCad”. Сформировать два вектора, которые описывают экспериментальные данные: VX, состоящий из значений толщин поглотителя  , и VY, содержащий соответствующие этим поглотителям значения функции пропуская , и VY, содержащий соответствующие этим поглотителям значения функции пропуская  . Построить график экспериментальной кривой пропускания в обычном и полулогарифмическом масштабе. . Построить график экспериментальной кривой пропускания в обычном и полулогарифмическом масштабе.
Задание 4.
Анализируя экспериментальную кривую 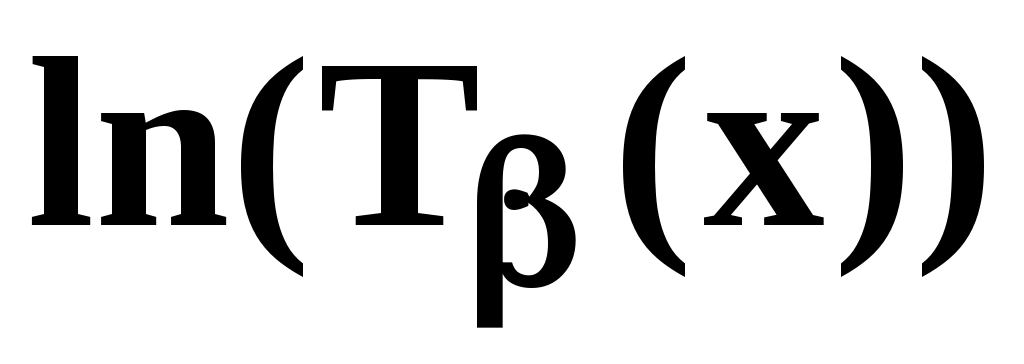 выделить центральный участок кривой и аппроксимировать его линейной функцией. Найти точку пересечения прямой с уровнем фона, т.е. выделить центральный участок кривой и аппроксимировать его линейной функцией. Найти точку пересечения прямой с уровнем фона, т.е.
значение  (см. Рис.4б). Используя Рис.5 определить максимальную энергию жесткой компоненты - спектра. (см. Рис.4б). Используя Рис.5 определить максимальную энергию жесткой компоненты - спектра.
Задание 5.
Аппроксимировать кривую пропускания экспоненциальной функцией и определить линейный коэффициент поглощения . Используя графическую зависимость от максимальной энергии - электронов (см. Рис.7) определить максимальную энергию жесткой компоненты - спектра источника, используя найденное значение (плотность алюминия = 2.7 г/см3 ). Сравнить полученный результат с энергией, найденной в Задании 4.
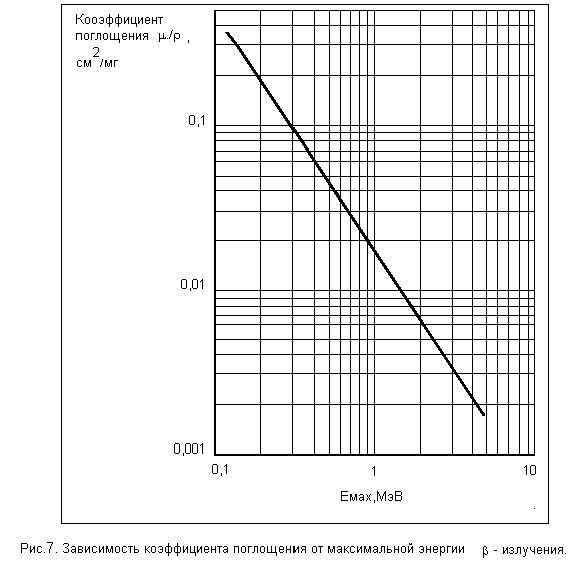
Рис.7. Зависимость коэффициента поглощения от максимальной энергии - излучения
5. Контрольные вопросы
Объясните зависимость от энергии электрона кривой ионизации.
Как определяется коэффициент массового поглощения?
В чем отличие кривых пропускания моноэнергетических электронов и β-электронов?
Почему для аппроксимации экспоненциальной функцией кривой пропускания электронов β-распада необходимо выбирать только ее среднюю часть?
Какие основные процессы потери энергии электронов в веществе?
Что такое дельта-электроны?
6. Литература
Альфа-, бета- и гамма-спектроскопия. Под.ред. К.Зигбана, М., 1969.
Экспериментальная ядерная физика Под ред Э.Сегрэ, т.1, М., 1955 г.
К.Н. Мухин Экспериментальная ядерная физика т.1, М., 1993г.
|
 Скачать 333.5 Kb.
Скачать 333.5 Kb.





 , (2)
, (2) , (4)
, (4)



