Лабораторная №9. Лабораторная работа 9 Определение ускорения свободного падения с помощью физического маятника ис203 Талатлы Б
 Скачать 182.67 Kb. Скачать 182.67 Kb.
|
|
Министерство образования и науки Республики Казахстан Карагандинский Государственный Технический Университет Кафедра ИВС Лабораторная работа №9 Определение ускорения свободного падения с помощью физического маятника Выполнил: ИС-20-3 Талғатұлы Б. . Проверила: Кузнецова Ю.А Караганда 2021г. Лабораторная работа № 9 Определение ускорения свободного падения с помощью физического маятника Цель работы: определение ускоре-ние свободного падения по кривой зависимости периода колебаний от положения точки подвеса маятника стержня. Приборы и принадлежности: экспериментальная установка, измери-тельная линейка, секундомер. Физическим маятником называется твёрдое тело, которое совершает колебания под действием своей силы тяжести mg вокруг неподвижной гори-зонтальной оси Oz, не проходящей через центр тяжести тела (рис. 1) и называе-мой осью качания маятника. 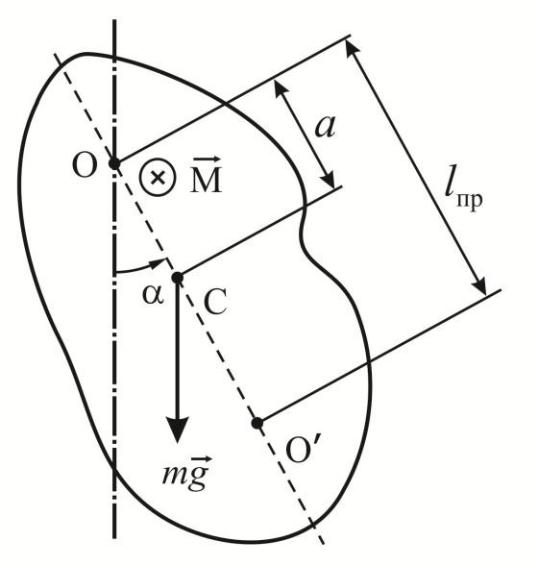 Рис. 1. Физический маятник: С — центр масс, О – точка подвеса, – расстояние от точки подвеса до центра масс; т - масса. Центр тяжести маятника совпадает с его центром масс C. Точка O пере-сечения оси качания маятника с вертикальной плоскостью, проходящей через центр тяжести маятника и перпендикулярной оси качания, называется точкой подвеса маятника. Моментом инерции твердого тела относительно оси называется скаляр-ная величина J, равная сумме произведений элементарных масс mi на квадраты их расстояний Ri2 от данной оси:
i 1 ВЫПОЛНЕНИЕ РАБОТЫ Таблица 1.
График 1. 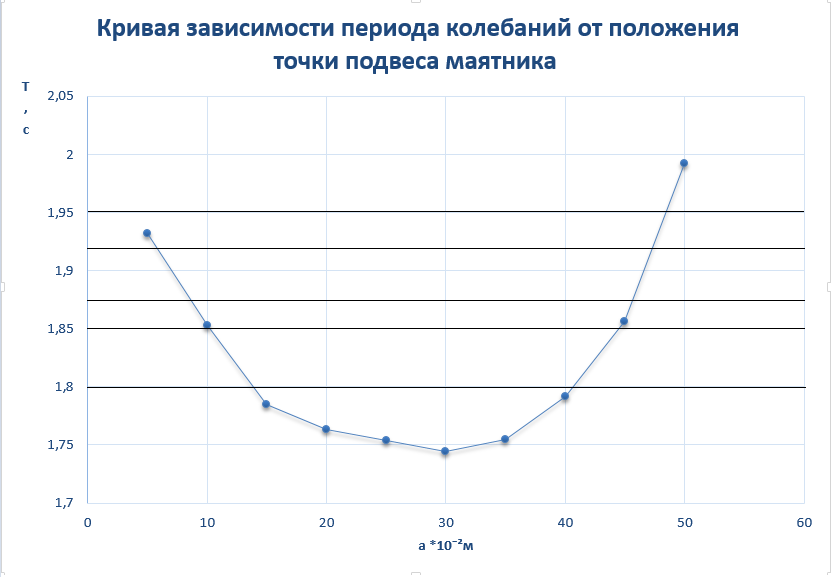
Таблица 2. Используемые формулы: T = t /N. l = а1+а2. gi = 4π2 l/T2 g = 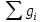 /n; /n; Δg = Sgtp.n., tp.n.-коэффициент Стьюдента tp.n = 2,776 , при n = 5,P=0.95 Sg = 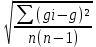 Контрольные вопросы. 1. Дайте определения колебания, периода, частоты, амплитуды, фазы, начальной фазы колебаний. Период колебания – промежуток времени, за который система совершает одно полное колебание (возвращается в первоначальное положение). Частота колебания – показывает количество колебаний в единицу времени. Амплитуда колебания – максимальное расстояние, на которое смещается колеблющееся тело от положения равновесия Фаза колебания – величина, определяющая отклонение тела от положения равновесия в данный момент времени. Начальная фаза колебания –значение фазы колебания в начальный момент времени (при t=0). 2. Дайте определение физического маятника. Объясните, почему ось качания физического маятника не должна проходить через центр инерции. Физический маятник — это твёрдое тело, которое совершает колебания под действием силы тяжести mg вокруг неподвижной горизонтальной оси Oz, не проходящей через центр тяжести тела и называемой осью качания маятника. Ось качания не должна проходить через центр инерции, так как в противном случае колебания будут отсутствовать. При отклонении маятника от положения равновесия на угол возникает вращательный момент сил, который стремится вернуть маятник в положение равновесия. 3. Приведите график зависимости периода колебаний физического маятника от расстояния. 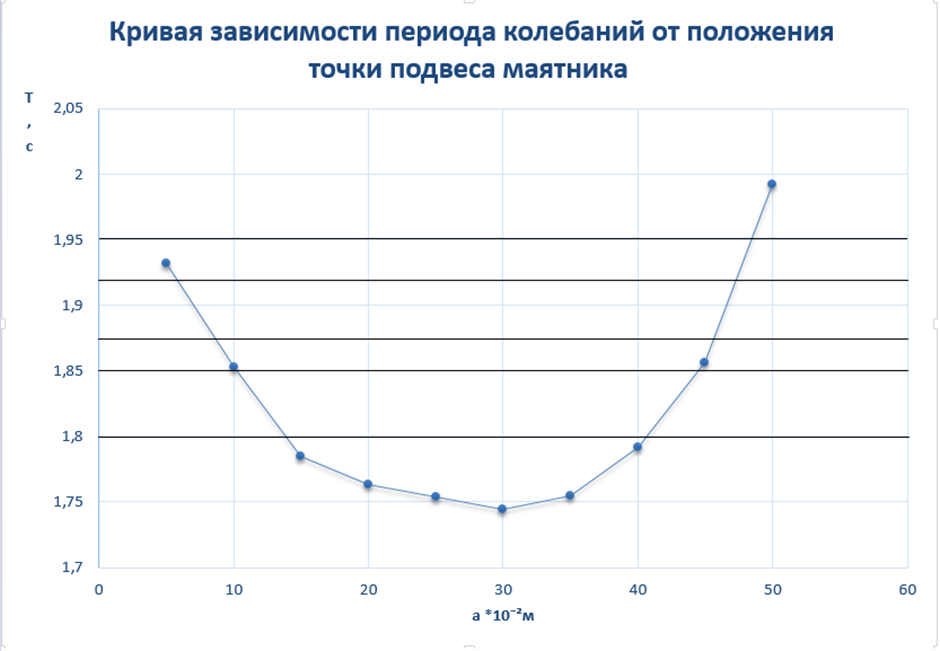 4. Выведите формулу (9). При отклонении маятника от положения равновесия на угол возникает вращательный момент сил, который стремится вернуть маятник в положение равновесия, который равен:M =–mg·a·sin, где m – масса маятника, a– расстояние от точки подвеса до центра инерции маятника. Обозначив момент инерции маятника относительно оси, проходящей через точку подвеса, буквой a, можно записать: M = JилиJ 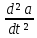 =– mg·a·sin a, =– mg·a·sin a,Исходя из этих уравнений следует, что при малых отклонениях от положения равновесия физический маятник совершает гармонические колебания, частота готорых зависит от массы маятника, момента инерции маятника относительно оси вращения и расстояния между осью вращения и центром инерции маятника. В связи с этим, период колебания физического маятника может определяться по формуле T = 2 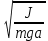 5. Сформулируйте теорему Штейнера. Если известен для тела момент инерции относительно оси, проходящей через центр тяжести, то момент инерции относительно оси параллельной ей определяется по формуле I = I0 + ma². I0 – момент инерции относительно оси, проходящей через центр тяжести а – расстояние между осями 6. Запишите дифференциальные уравнения незатухающих, затухающих и вынужденных колебаний. Дифференциальное уравнение незатухающих колебаний 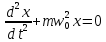 Дифференциальное уравнение затухающих колебаний 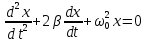 Дифференциальное уравнение вынужденных колебаний 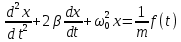 7. Дайте определение момента инерции твёрдого тела. Моментом инерции твердого тела относительно оси называется скалярная величина J, равная сумме произведений элементарных масс mi на квадраты их расстояний Ri2 от данной оси: J mi Ri2. |
