Лабораторная работа. Лабораторная работа 9 виртуальное испытание круглого бруса на кручение
 Скачать 0.8 Mb. Скачать 0.8 Mb.
|
|
Лабораторная работа № 9 ВИРТУАЛЬНОЕ ИСПЫТАНИЕ КРУГЛОГО БРУСА НА КРУЧЕНИЕ 1. ЦЕЛЬ РАБОТЫ Установить зависимость угла закручивания от крутящего. Определить касательные и главные напряжения при кручении. Испытания позволят визуализировать процесс напряжений в образце в разный период времени с указанием нагрузки в конкретном месте. 2. ОБОРУДОВАНИЕ И ИНСТРУМЕНТЫ 1) ЭВМ 2) Autodesk Inventor Professional 2021 3) Принтер 3. ТЕОРЕТИЧЕСКОЕ ОБОСНОВАНИЕ При кручении в поперечных сечениях бруса действуют только крутящие моменты Тк. Поперечные сечения поворачиваются вокруг оси бруса, длина бруса при этом не изменяется. Во всех точках прямого круглого бруса создается напряженное состояние чистого сдвига. Закон Гука при сдвиге выражает прямую пропорциональную зависимость между касательным напряжением и углом сдвига : =G, (1) где G - модуль сдвига (модуль упругости второго рода), характеризующий жесткость материала при действии касательных напряжений. При кручении в поперечных сечениях бруса возникают касательные напряжения 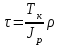 , (2) , (2)где Jp - полярный момент инерции поперечного сечения, - расстояниеот центра сечения до рассматриваемой точки. Наибольшие напряжения maxдействуют на наибольшем расстоянии max от центра сечения в непосредственной близости к наружной боковой поверхности бруса. Распределение напряжений кручения в поперечном сечении сплошного круглого бруса в центральной части сечения материал нагружен мало. С целью экономии материала и снижения массы нередко применяют брусья кольцевого сечения. При одинаковой массе прочность и жесткость на кручение бруса с кольцевым поперечным сечением существенно выше, чем у бруса со сплошным поперечным сечением. Угол закручивания бруса  , (3) , (3)где l длина рассматриваемого участка бруса. Произведение GJp называют жесткостью сечения при кручении. Зависимости справедливы в пределах пропорциональности. Для сплошного круглого сечения Jp=d4 32, (4) где d - диаметр бруса. Для кольцевого сечения Jp= (D4- d4) 32, (5) где Dи d- соответственно наружный и внутренний диаметры бруса.  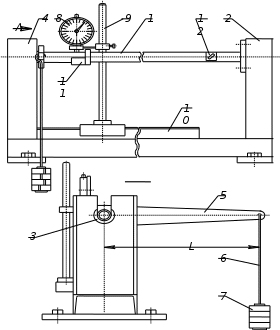 Рис. 1 Jpи max для каждого сечения постоянны и могут быть объединены геометрической характеристикой Wp=Jpmax, которая называется полярным моментом сопротивления. Тогда наибольшие касательные напряжения кручения 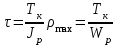 . (6) . (6)Для сплошного круглого сечения max=d 2 и Wp=d3 16, (7) для кольцевого сечения max=D 2 и 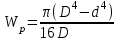 . (8) . (8)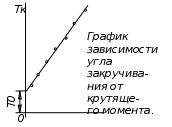 В пределах пропорциональности углы поворота поперечных сечений бруса изменяются в зависимости от крутящего момента по линейной зависимости (рис. 26). Некоторые отклонения точек, нанесенных на график по результатам эксперимента, от линейной зависимости, связаны с неточностями постановки опыта и ошибками измерений. Для того, чтобы устранить влияние зазоров и контактных деформаций в соединениях на результаты эксперимента, брус предварительно нагружается начальным моментом Т0. При достаточной величине этого момента стрелка индикатора 8 начинает отклоняться. В ходе эксперимента производится ступенчатое нагружение бруса, что позволяет выявить случайную ошибку измерений. Для каждого нагружения определяются Тiи φi, для каждого интервала нагружения вычисляются приращения момента ΔТi=Тi- Ti-1 и угла закручивания Δφi=φi - φi-1. За наиболее вероятное значение измеряемой величины принимается ее среднее арифметическое значение. Среднее значение приращения крутящего момента 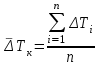 , (9) , (9)где п - число интервалов измерения. Среднее значение приращения угла закручивания 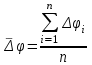 . (10) . (10)На основании (6.5) можно вычислить модуль сдвига: 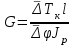 . (11) . (11)Для оценки величины случайной ошибки вычисляется среднеквадратичная ошибка и принимается доверительная вероятность. Среднеквадратичная ошибка измерения угла закручивания  . (6.14) . (6.14)Доверительной вероятностью, или коэффициентом надежности α называется вероятность того, что результат измерения не выходит за пределы доверительного интервала. Доверительным интервалом называется интервал значений от x-Δxдо x+Δx. В данной работе под x понимается истинное значение Δφ.Обычно на практике α принимают 0,9 или 0,95. Для числа измерений п величина ошибки 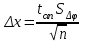 , (6.15) , (6.15)где tαn - коэффициент Стьюдента, определяется по входным параметрам п и α (Приложение 2). Расхождение между опытным и теоретическим значениями угла закручивания  . .В соответствии с законом парности касательных напряжений в продольных сечениях бруса действуют касательные напряжения, равные по величине напряжениям в поперечных сечениях, но противоположные по знаку. Максимальные 1=maxи минимальные 3=min нормальные напряжения называются главными напряжениями, а площадки, по которым они действуют, главными площадками. Касательные напряжения по главным площадкам равны нулю. Главные площадки наклонены под углом 450 к площадкам чистого сдвига, т.е. к поперечному и продольному сечениям бруса, подверженному кручению. Численно главные напряжения равны экстремальным касательным напряжениям. Наибольшие по величине экстремальные касательные и главные напряжения действуют в непосредственной близости от внешней поверхности бруса и могут быть определены по формуле: max= - min=max = - min = Tк Wp. (6.16) Жесткость бруса при кручении характеризуется относительным углом закручивания =l, рад/м, или θ0 = θ·1800⁄ π, град⁄м. (6.17) Потенциальная энергия при кручении 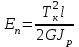 . (6.18) . (6.18)4. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ https://youtu.be/8KYToSmOvxs 0. Разбиться на 4 рабочие группы и выбрать цель исследования: - Сравнение образцов одной геометрии, но из разных материалов. - Сравнение образцов с разной геометрией, но из одинаковых материалов - Выбрать несколько одинаковых настроек сетки, значения сил - Моделирование кольцевого и круглого профиля - Моделирование разной длины плеча - Моделирование плеча на разном расстоянии от крепления 1. Подготовить 3D-модель по образцу как на рисунке 2 (со своими геометрическими данными). Обратить внимание на крепление 1 – стандартное защемление; крепление 2 – шарнирное (есть упор, но нет ограничений по вращению вдоль главной оси образца); на место приложения силы. (см ЛР№5, п. 4.6)  Рис. 2 2. Провести моделирование статической нагрузки для выбранных параметров в пункте 0. 3. Проанализировать полученные результаты. 5. ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ Оформить в свободном стиле сравнительный анализ данных, полученных в ходе проведения исследований всеми рабочими группами (пункт 4.0). Написать в выводы и рекомендации по возможным местам применения данной схематичной модели, а также рекомендации по геометрической форме для разных целей применения, с учётом мест максимальных нагрузок. |
