Пример. Пример решения задания 3. Решение Заданная схема показана на рисунке Определяем скручивающие моменты

• Название: Решение Заданная схема показана на рисунке Определяем скручивающие моменты
• Анкор: Пример
• Дата: 16.02.2022
• Размер: 63.84 Kb.
• Имя файла: Пример решения задания 3.docx
• Тип: Решение; #364166

Пример решения задания 3

Р 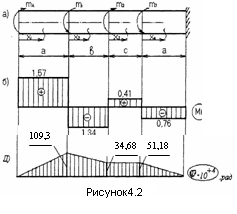ассмотрим пример расчета вала

Для стального вала требуется:

1.Найти через известные мощности Р_i,, сответствующие скручивающие моменты m_i;
2.Найти известный момент m_A из условия равенства нулю угла закручивания свободного конца вала;
3.Построить эпюру крутящих моментов М_к;

4.Подобрать круглое сечение из условия прочности;
5.Построить эпюру углов поворота 
Решение:
Заданная схема показана на рисунке 4.2.

1. 
   Определяем скручивающие моменты: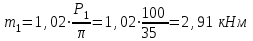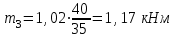
   

;

;

.

2 Значение неизвестного момента m_A найдем из того условия, что угол закручивания свободного конца вала равен нулю, т.е. _А=0. Для удобства счета разобьем этот угол на составляющие, зависящие от каждого скручивающего момента, т.е. φ_А = φ_тА⁺ φ_mА⁺ φ_т2⁺ φ_m3= 0 ,

где φ_тА - угол поворота концевого сечения от действия только момента т_a,φ_m1- то же, но от действия только момента m₁;

φ_m2 - от действия только момента т₂; φ_т3 - от действия только момента m₃;

т.е.



Подставив числовые значения, после преобразований, получим

т_A = 1,57 кНм

3. 
   Пользуясь методом сечений, определяем величины крутящих моментов на отдельных участках вала.
   

Участок 1 0 ≤Х₁≤ а;

М_K1= +т_А = +1,57 кНм Участок 2 0 ≤ X₂ ≤ b;

М_К2= т_А–т₁=1,57 - 2,91 = -1,34кНм Участок 3 0 ≤ X₃≤с;

М_K3 = т_А–т₁ + m₂=1,57 - 2,91 +1,75 = 0,41кНм Участок 4 0 ≤ Х₄≤а;

М_К4 = т_А–т₁+т₂ – т₃ = 1,57 - 2,91 +1,75 -1,17 = -0,76кНм По полученным значениям крутящих моментов строим эпюру М_к (рис. 1,б).

4 Определим диаметр вала из условия прочности по максимальному крутящему моменту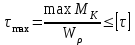

,

где W_=0,2 D³

Тогда 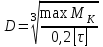= =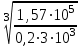6,4 см=64 мм. округляя до стандартного, получаем

D=65 мм D=6,5 см
5 Вычислим углы поворота «»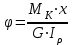



Участок 1. 0  х₁  а=1 м=100 см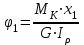

;

х₁=0 х₁=1,0 м

₁=0 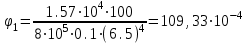рад.

Участок 2 0  х₂  в=0,8 м=80 см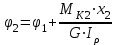



х₂=0 х₂ = в=0,8 м=80 см

₂=₁=109,3310^-4 рад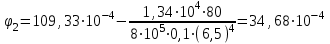

рад.
Участок 3 0  х₃  с=0,6 м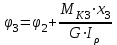

;

х₃=0; х₃  с=0,6 м=60 см

₃=₂=34,6810^-4 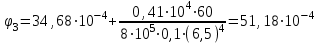рад; рад.
Участок 4 0  х₄  а=1,0 м=100 см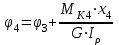

;

х₄=0; х₄=100 см;

₄=₃=51,1810^-4 рад;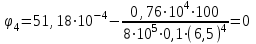

По полученным значениям _I строим эпюру углов поворота «» (рисунок 3.2).