|
|
лаб 4. лаб4. Лабораторная работа аппроксимация функциональной зависимости, заданной таблично, в задачах планирования траектории движения робототехнических и мехатронных систем
ЮРГПУ(НПИ)
|
ЛАБОРАТОРНАЯ РАБОТА
АППРОКСИМАЦИЯ ФУНКЦИОНАЛЬНОЙ ЗАВИСИМОСТИ, ЗАДАННОЙ ТАБЛИЧНО, В ЗАДАЧАХ ПЛАНИРОВАНИЯ ТРАЕКТОРИИ ДВИЖЕНИЯ РОБОТОТЕХНИЧЕСКИХ И МЕХАТРОННЫХ СИСТЕМ
|
4
В1
|
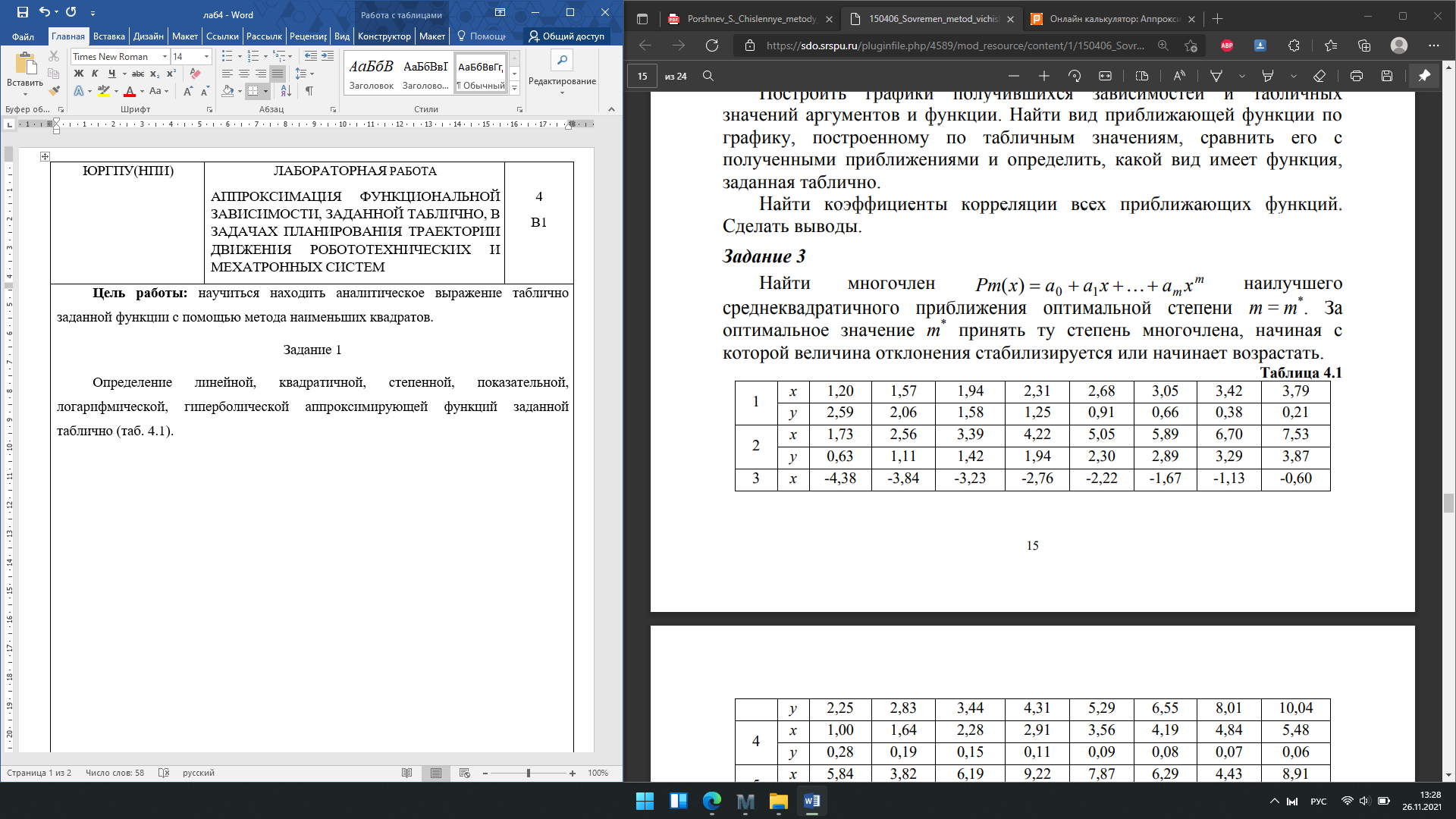
Цель работы: научиться находить аналитическое выражение таблично заданной функции с помощью метода наименьших квадратов.
Определение линейной, квадратичной, степенной, показательной, логарифмической, гиперболической аппроксимирующей функций заданной таблично (таб. 4.1).
Линейная регрессия
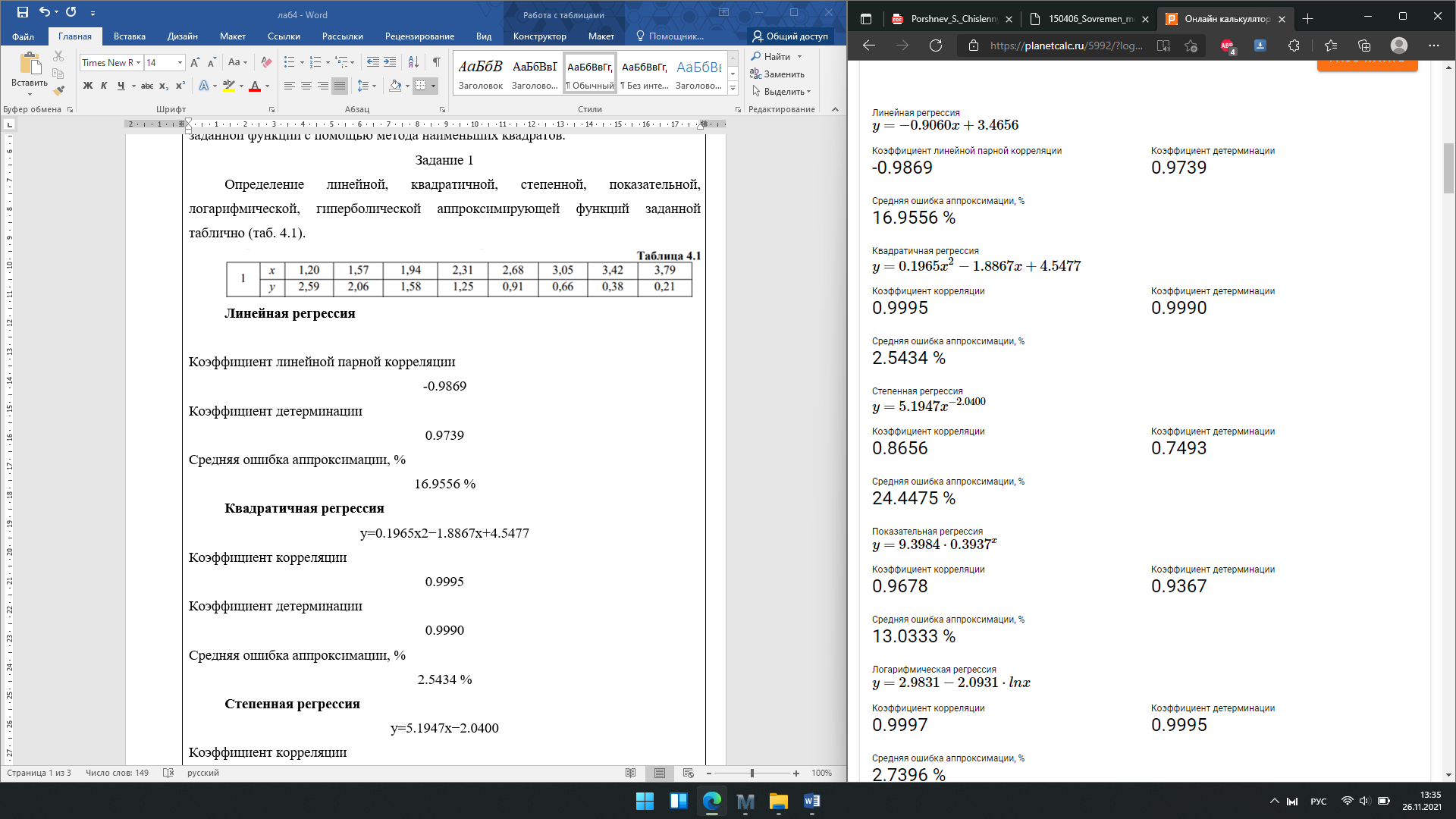
Коэффициент линейной парной корреляции
-0.9869
Коэффициент детерминации
0.9739
Средняя ошибка аппроксимации, %
16.9556 %
Квадратичная регрессия

Коэффициент корреляции
0.9995
Коэффициент детерминации
0.9990
Средняя ошибка аппроксимации, %
2.5434 %
Степенная регрессия

Коэффициент корреляции
0.8656
Коэффициент детерминации
0.7493
Средняя ошибка аппроксимации, %
24.4475 %
Показательная регрессия

Коэффициент корреляции
0.9678
Коэффициент детерминации
0.9367
Средняя ошибка аппроксимации, %
13.0333 %
Логарифмическая регрессия

Коэффициент корреляции
0.9997
Коэффициент детерминации
0.9995
Средняя ошибка аппроксимации, %
2.7396 %
Гиперболическая регрессия

Коэффициент корреляции
0.9854
Коэффициент детерминации
0.9711
Средняя ошибка аппроксимации, %
19.6062 %
В результате получим график аппроксимирующих функций:
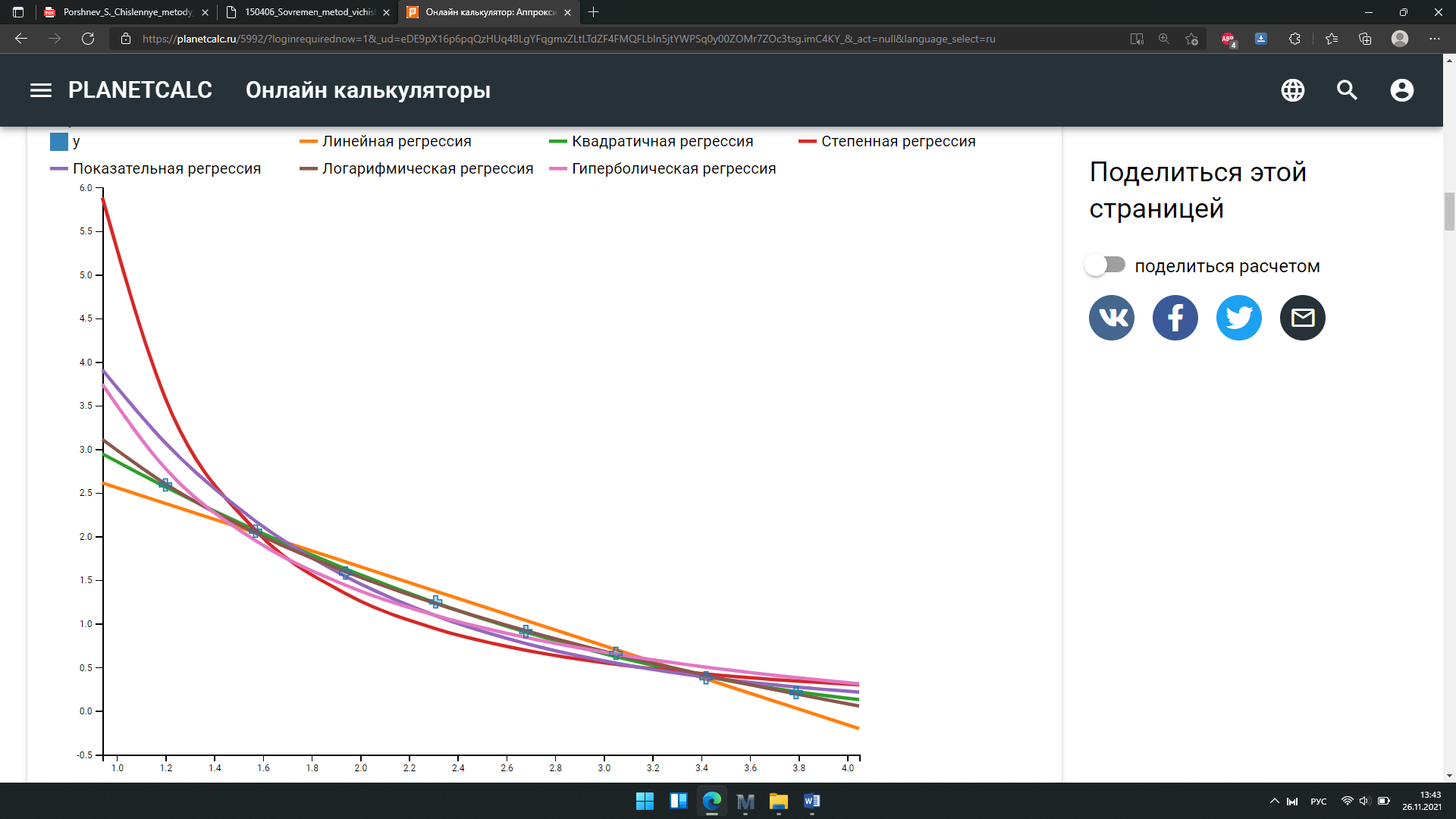
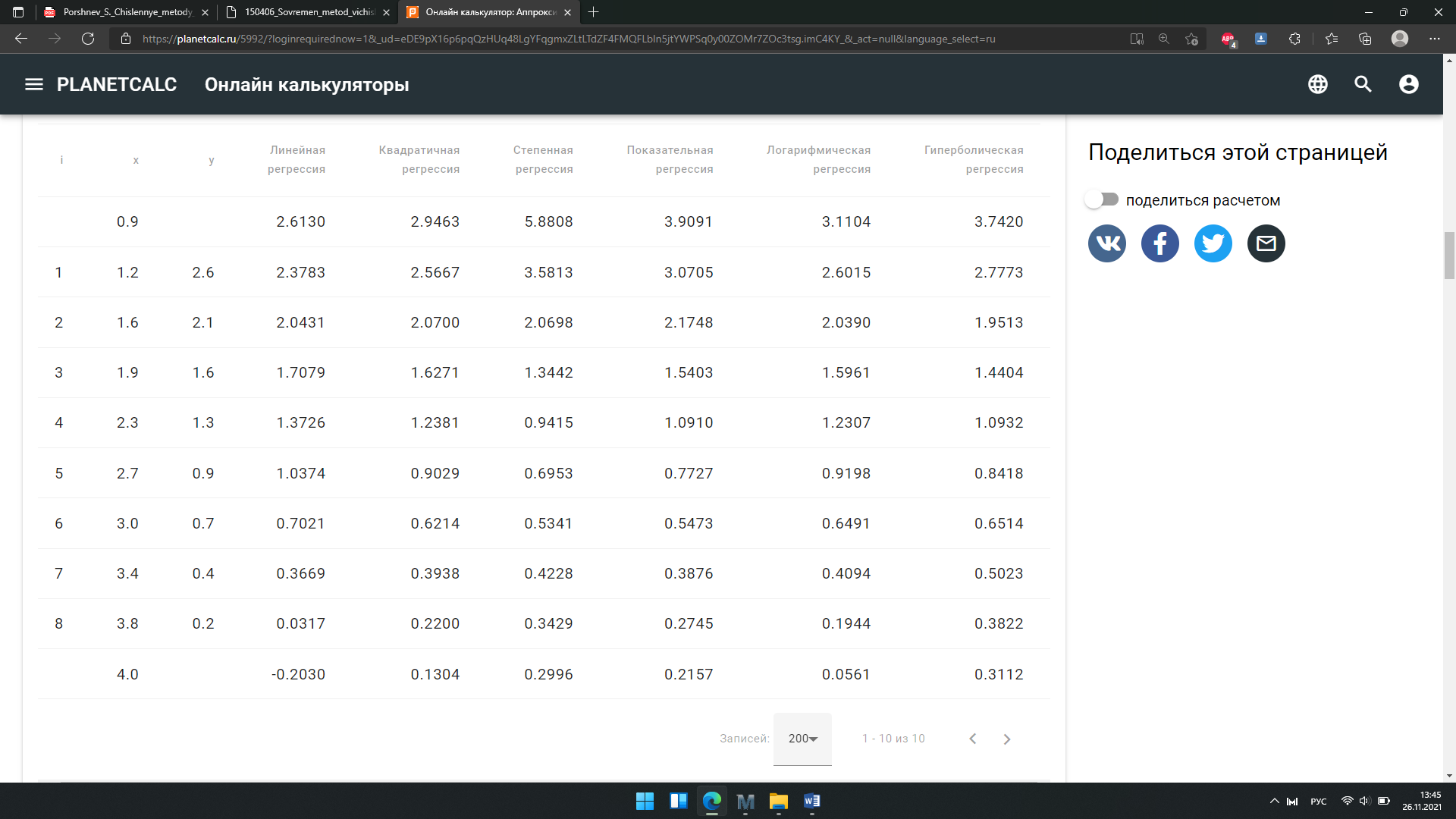
Линейное уравнение регрессии:

Коэффициент a:

Коэффициент b:
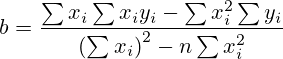
Коэффициент линейной парной корреляции:
Коэффициент детерминации:

Средняя ошибка аппроксимации:
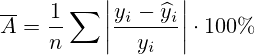
Квадратичное уравнение регрессии:
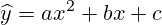
Система уравнений для нахождения коэффициентов a, b и c:
Коэффициент корреляции:
 , ,
Где

Коэффициент детерминации:

Средняя ошибка аппроксимации:
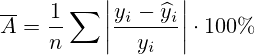
Степенное уравнение регрессии:

Коэффициент b:

Коэффициент a:
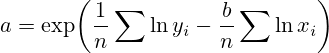
Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.
Показательное уравнение регрессии:

Коэффициент b:

Коэффициент a:

Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.
Гиперболическое уравнение регрессии:

Коэффициент b:

Коэффициент a:

Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации - используются те же формулы, что и для квадратичной регрессии.
Логарифмическое уравнение регрессии:
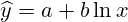
Коэффициент b:

Коэффициент a:

Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации - используются те же формулы, что и для квадратичной регрессии.
|
Работу выполнил
Студент
Васильев А.Н.
|
Работу принял
Притчина М.Д.
|
Дата
| |
|
|
 Скачать 1.21 Mb.
Скачать 1.21 Mb.