Эконометрика КПИ _вар 5. Лабораторная работа Линейная регрессия с двумя переменными 3 Лабораторная работа Множественная регрессия 16
 Скачать 478 Kb.
|
1 2 Лабораторная работа 2. Множественная регрессияПостановка задачи Имеются данные по рейтингу компаний мира Forbes-2000 (за 2009 год). Эксперты определяют их положение в рейтинге на основе рыночной стоимости, активов, доходов и объёмов продаж. Требуется построить множественную регрессию зависимости рыночной стоимости компании от активов, доходов и объёмов продаж и провести её анализ. Требуется: Провести анализ регрессии и построить линию регрессии (линию прогноза); Построить укороченную модель регрессии и сравнить ее с полной регрессией; Провести проверку модели регрессии. Входные данные (в соответствии с последовательностью переменных):
Выполнение 1. Анализ регрессии и построение линии регрессии (линии прогноза). Создание таблицы с параметрами регрессии. Копируем данные своего варианта на отдельный лист Excel - Множественная регрессия. Множественная регрессия дает представление о точности предикторов при их совместном использовании. В данной работе используется следующая модель множественной регрессии: Рыночная стоимость компании =  +  (Активы) +  (Доходы) +  ( Объём продаж) +  .Чтобы выполнить анализ множественной регрессии, прибегнем к команде Регрессия модуля Пакет анализа. 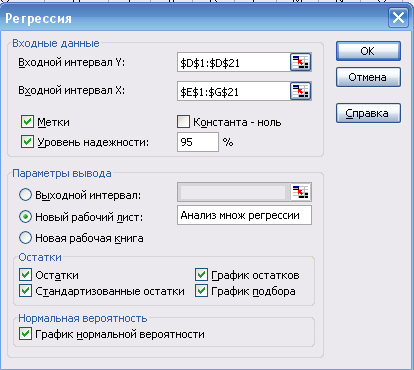 Получаем: 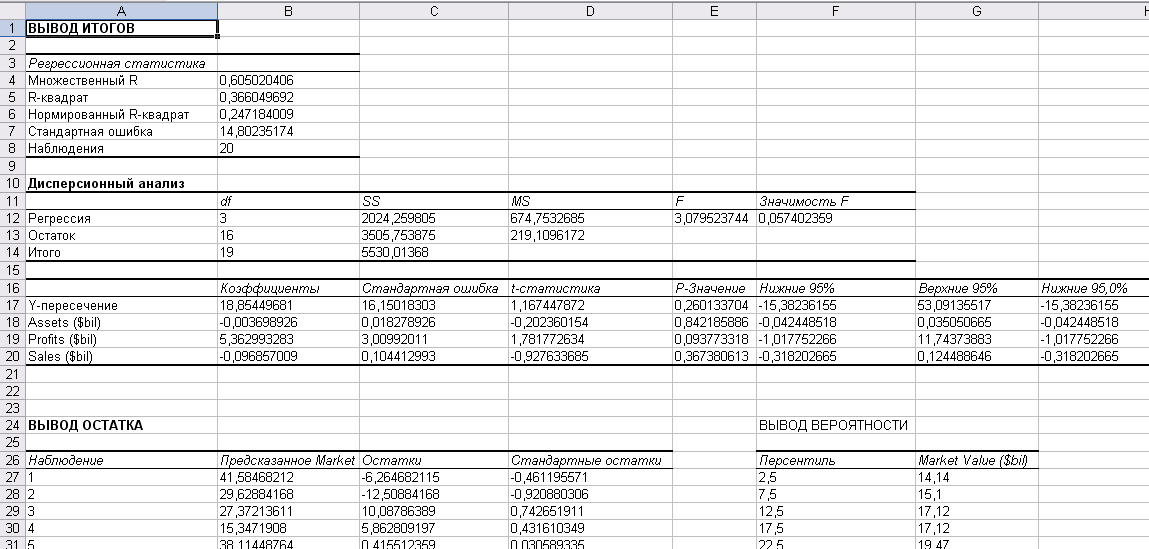 Рис. 1. Результат выполнения команды Регрессия Исходя из полученного отчета Excel, заполним столбец «Полная регрессия:
Получили зависимость: Y (Рыночная стоимость компании) = 0,26 + 0,842Х1(Активы) + 0,094 Х2(Доходы) + 0,367 Х3( Объём продаж). Значение R-квадрат = 0,366 говорит о слабой зависимости между переменными. Интерпретация итоговых параметров регрессии Для интерпретации итоговых параметров регрессии рассмотрим сначала таблицу 2 Дисперсионный анализ:  В таблице анализа дисперсии содержится информация о статистической значимости подогнанной модели регрессии. Дисперсионный анализ основывается на следующих гипотезах: ■ нулевая гипотеза  : коэффициенты регрессии для всех трёх предикторов равны 0;■ альтернативная гипотеза  : по крайней мере один из трёх коэффициентов регрессии не равен 0.В данной работе нужно сконцентрироваться только на F-отношении и Р-значении (Значимость F), которые определяют статистическую значимость регрессии. Значимость нулевой гипотезы может быть проверена двумя способами. 1 способ. В ячейке Е12 приводится значение 3,08 для F-отношения. Для проверки нулевой гипотезы нужно сравнить вычисленное значение F-отношения с критическим значением F*. Для получения визуального представления этой гипотезы используем рабочий лист F-распределения из рабочей книги Распределения. xls и отобразим в нём распределение F (3,16) (значения 3 и 16 - это первые два элемента столбца df таблицы Дисперсионный анализ).  Поскольку F = 3,08 < F* = 3,239 , то нулевая гипотеза не может быть отклонена. 2 способ. В столбце Значимость F, в ячейке F12, приводится значение 0,057. Это значение выше 0,05, т.е. регрессия не имеет статистическую значимость на уровне 5%. Иными словами, нулевую гипотезу невозможно отвергнуть на уровне статистической значимости 5% и мы не можем принять альтернативную гипотезу. Если F-отношение не имеет достаточную статистическую значимость, то нет смысла интересоваться остальными результатами анализа. Построенная регрессия не состоятельна. На этом анализ заканчивается. Выводы по работе: В ходе выполнения данной работы был проведён анализ регрессии и построена множественная модель линейной регрессии - зависимости рыночной стоимости компании от активов, доходов и объёмов продаж: Y (Рыночная стоимость компании) = 0,26 + 0,842Х1(Активы) + 0,094 Х2(Доходы) + 0,367 Х3( Объём продаж). Значения множественного коэффициента корреляции R и коэффициента детерминации (R-квадрат) далеки от единицы, что говорит о слабой зависимости между переменными. Дисперсионный анализ подтверждает, что построенная регрессия не состоятельна. Очевидно, зависимость является более сложной (нелинейной). Список использованной литературыБородич С.А. Эконометрика: Учеб. Пособие для студ. эконом. спец. вузов/С.А. Бородич. – Минск: Новое знание, 2001. – 407с. Магнус Я.Р., Катышев П.К., Пересецкий А.А. Эконометрика. Начальный курс: Учебник. – 7-е изд., испр. – М.: Дело, 2005. Практикум по эконометрике: Учеб. Пособие /И.И. Елисеева, С.В. Курышева, Н.М. Гордеенко и др.; Под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2006. Д. Ханк, А. Райтс,. Д. Уитчер, Бизнес-прогнозирование, Вильямс, Москва, Санкт-Перербург, Киев, 2003 Эконометрика: Учебник/ И.И. Елисеева, С.В. Курышева, Т.В. Костеева и др.; Под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М: Финансы и статистика, 2005. 1 2 |