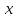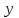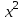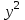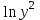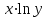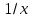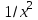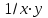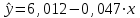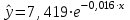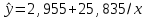Эконометрика. Контрольная работа. 3 курс. Эконометрика. КР 3 курс. Контрольная работа по дисциплине Эконометрика Вариант 1 Содержание задача парная регрессия 2 задача множественная регрессия и корреляция 13
 Скачать 4.43 Mb. Скачать 4.43 Mb.
|
|
Федеральное государственное образовательное бюджетное учреждение высшего образования ФИНАНСОВЫЙ УНИВЕРСИТЕТ ПРИ ПРАВИТЕЛЬСТВЕ РОССИЙСКОЙ ФЕДЕРАЦИИ Ярославский филиал Финуниверситета Кафедра «Экономика и финансы» Контрольная работа по дисциплине «Эконометрика» Вариант 1 СодержаниеЗАДАЧА 1. Парная регрессия 2 ЗАДАЧА 2. Множественная регрессия и корреляция 13 ЗАДАЧА 3. Временные ряды 26 ЗАДАЧА 1. Парная регрессияТребуется: 1. Для характеристики y от x построить следующие модели: - линейную, - экспоненциальную, - гиперболическую. 2. Оценить каждую модель, определив: - индекс корреляции, - коэффициент детерминации, - F-критерий Фишера. 3. Составить сводную таблицу вычислений, выбрать лучшую модель, дать интерпретацию рассчитанных характеристик. 4. По лучшей модели рассчитать прогнозные значения результативного признака, если прогнозное значение фактора увеличится на 10% относительно его среднего уровня. 5. На графике отобразить диаграмму рассеяния, график лучшей модельной кривой и прогнозное значение. Дано: х – имущество (в тыс. $) семи случайно выбранных семей, у – накопления (в тыс. $).
(вариант 1) Решение: Выполним построение линейной модели. Составим для этого таблицу 1. Для начала следует найти дисперсию и среднее квадратическое отклонение. Они помогут нам в решении задачи. Таким образом, найдем дисперсию: 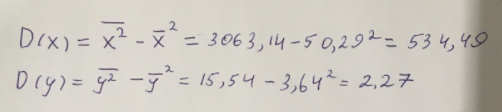 Далее выясним среднее квадратическое отклонение: 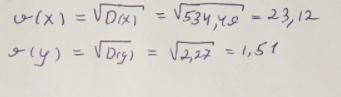 Таблица 1. – Вычисление для линейной модели зависимости накоплений (y) от имущества случайно выбранной семьи (x).
Линейное уравнение парной регрессии имеет вид: 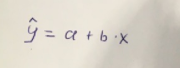 Используем метод наименьших квадратов для нахождения необходимых параметров: 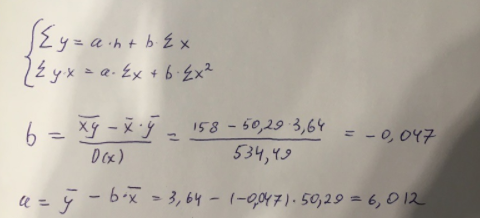 Итак, линейное уравнение парной регрессии будет: 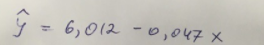 Найдем индекс корреляции для нахождения зависимости между показателями: 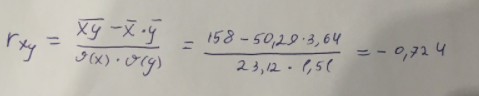 Мы видим, что значение индекса корреляции в диапазоне от 0,7 до 0,9. А значит можем сделать вывод о тесной линейной зависимости между накоплениями (y) и стоимость имущества семьи (x). Далее выполним расчет коэффициента детерминации для оценки качества модели: 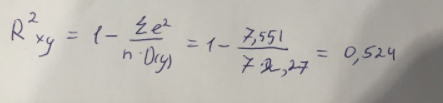 Значение коэффициента составляет 0,524. Также оно довольно сильно отклоняется от 1. Выводом для нас будет то, что мы не видим высокого качества линейной модели уравнения регрессии. К тоже она объясняет 52,4% вариации накоплений (значений y) в зависимости от изменения стоимости имущества семьи (x). Найдем F-критерий Фишера для определения значимости уравнения: 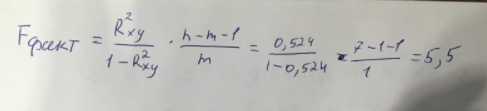 Табличное значение F-критерия мы найдем по таблице Фишера: = 0,05 (уровень значимости); к1 = n – m – 1 = 7 – 1 – 1 = 5; к2 = m = 1. Fтабл = 6,60 Теперь сравним фактическое и табличное значения F-критерия. Получим: Fфакт < Fтабл (5,50 < 6,60) Как итог, мы видим линейное уравнение регрессии не является значимым. Выполним построение экспоненциальной модели. Составим для этого таблицу 2. Для начала следует найти дисперсию и среднее квадратическое отклонение. Они помогут нам в решении задачи. Таким образом, найдем дисперсию: 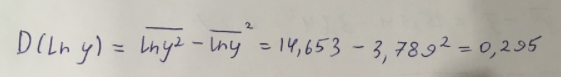 Далее выясним среднее квадратическое отклонение: 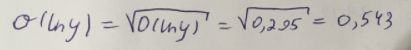 Таблица 2. – Вычисление для экспоненциальной модели зависимости накоплений (y) от имущества случайно выбранной семьи (x).
Экспоненциальное уравнение парной регрессии имеет вид: 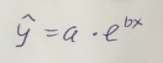 При этом линеаризация: 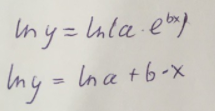 Используем метод наименьших квадратов для нахождения необходимых параметров: 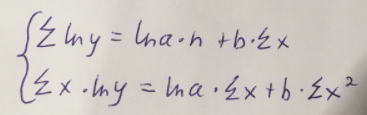 Следующим шагом найдем параметры: 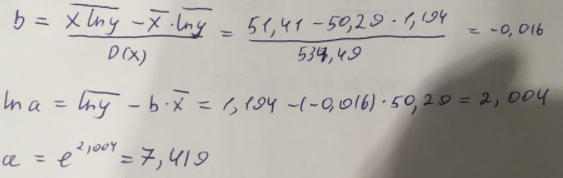 Итак, экспоненциальное уравнение парной регрессии будет: 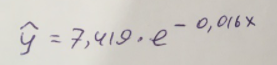 Найдем индекс корреляции для нахождения зависимости между показателями: 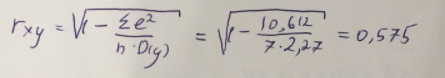 Мы видим, что значение индекса корреляции в диапазоне от 0,5 до 0,7. А значит в экспоненциальной модели мы можем сделать вывод о заметной зависимости между накоплениями (y) и стоимость имущества семьи (x). Далее выполним расчет коэффициента детерминации для оценки качества модели: 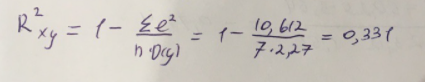 Значение коэффициента составляет 0,331. Также оно очень сильно отклоняется от 1. Выводом для нас будет то, что мы не видим высокого качества линейной модели уравнения регрессии. К тоже она объясняет 33,1% вариации накоплений (значений y) в зависимости от изменения стоимости имущества семьи (x). Найдем F-критерий Фишера для определения значимости уравнения: 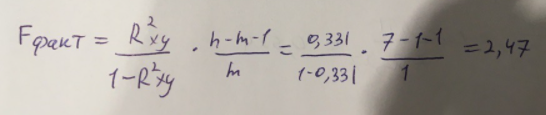 Табличное значение F-критерия мы найдем по таблице Фишера: = 0,05 (уровень значимости); к1 = n – m – 1 = 7 – 1 – 1 = 5; к2 = m = 1. Fтабл = 6,60 Теперь сравним фактическое и табличное значения F-критерия. Получим: Fфакт < Fтабл (2,47 < 6,60) Как итог, мы видим экспоненциальное уравнение регрессии не является значимым. Выполним построение гиперболической модели. Составим для этого таблицу 3. Для начала следует найти дисперсию и среднее квадратическое отклонение. Они помогут нам в решении задачи. Таким образом, найдем дисперсию: 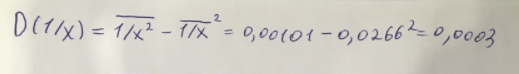 Далее выясним среднее квадратическое отклонение: 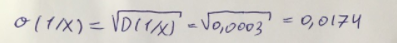 Таблица 3. – Вычисление для гиперболической модели зависимости накоплений (y) от имущества случайно выбранной семьи (x).
Гиперболическое уравнение парной регрессии имеет вид: 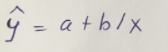 Используем метод наименьших квадратов для нахождения необходимых параметров: 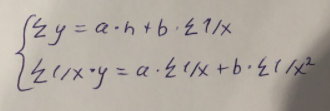 Следующим шагом найдем параметры: 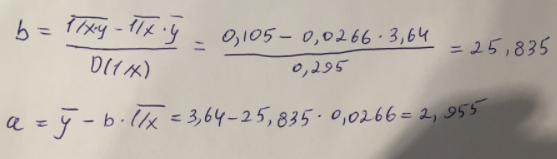 Итак, гиперболическое уравнение парной регрессии будет: 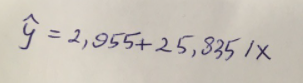 Найдем индекс корреляции для нахождения зависимости между показателями: 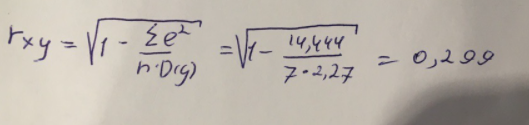 Мы видим, что значение индекса корреляции в диапазоне от 0,1 до 0,3. А значит в гиперболической модели мы можем сделать вывод о слабой зависимости между накоплениями (y) и стоимость имущества семьи (x). Далее выполним расчет коэффициента детерминации для оценки качества модели: 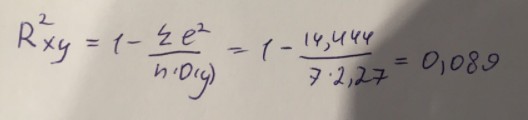 Значение коэффициента составляет 0,0,089. Также оно очень сильно отклоняется от 1. Выводом для нас будет то, что мы не видим высокого качества линейной модели уравнения регрессии. К тоже она объясняет 8,9% вариации накоплений (значений y) в зависимости от изменения стоимости имущества семьи (x). Найдем F-критерий Фишера для определения значимости уравнения: 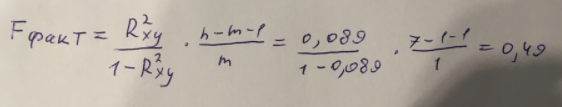 Табличное значение F-критерия мы найдем по таблице Фишера: = 0,05 (уровень значимости); к1 = n – m – 1 = 7 – 1 – 1 = 5; к2 = m = 1. Fтабл = 6,60 Теперь сравним фактическое и табличное значения F-критерия. Получим: Fфакт < Fтабл (0,49 < 6,60) Как итог, мы видим, что гиперболическое уравнение регрессии не является значимым. Для последующего анализа и выведения итогов составим общую таблицу 4. Таблица 4 – Парные уравнения регрессии зависимости накоплений (y) от имущества случайно выбранной семьи (x).
Проанализировав показатели, мы можем видеть, что наилучший результат (максимальный коэффициент детерминации и значение F-критерия Фишера) из предложенных вариантов дает линейная модель. Составим прогноз: 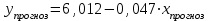 При 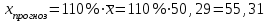 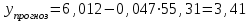 Для наглядности отобразим на графике диаграмму рассеяния, график выбранной модельной кривой (линейной) и прогнозное значение: 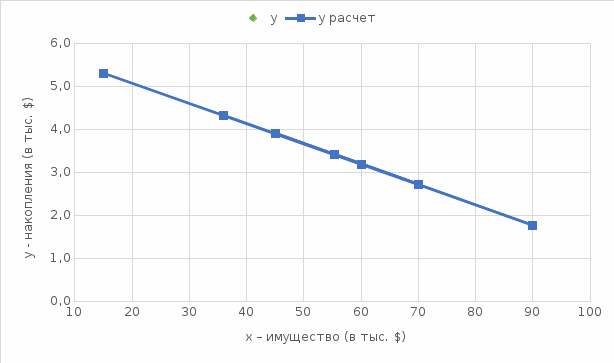 Рисунок 1 – График зависимости накоплений (y) от имущества случайно выбранной семьи (x) |