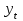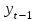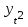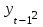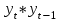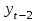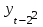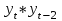Главная страница
Навигация по странице:

  • 0,393 0,329

  • 0,627 0,574

  • 0,337 0,242

  • 0,580 0,492

    		•

    Эконометрика. Контрольная работа. 3 курс. Эконометрика. КР 3 курс. Контрольная работа по дисциплине Эконометрика Вариант 1 Содержание задача парная регрессия 2 задача множественная регрессия и корреляция 13


    Скачать 4.43 Mb.
    НазваниеКонтрольная работа по дисциплине Эконометрика Вариант 1 Содержание задача парная регрессия 2 задача множественная регрессия и корреляция 13
    АнкорЭконометрика. Контрольная работа. 3 курс
    Дата29.04.2023
    Размер4.43 Mb.
    Формат файлаdocx
    Имя файлаЭконометрика. КР 3 курс.docx
    ТипКонтрольная работа
    #1097643
    страница3 из 5
    1   2   3   4   5

    ЗАДАЧА 3. Временные ряды


    Имеются условные данные об изменении результирующего показателя 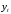для соответствующих моментов (уровней) времени t.

    Требуется:

    1. Построить аддитивную модель временного ряда (для нечетных вариантов) или мультипликативную модель временного ряда (для четных вариантов),

    2. Сделать прогноз на 2 уровня вперед.

    Дано: t- годы; yt – собственная продукция

    t
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10

    yt
    1,3
    1,4
    1,5
    1,7
    2,1
    2,2
    2,5
    2,7
    3,0
    3,3

    (вариант 1)

    Под аддитивной моделью временного ряда подразумевают такую модель, в которой уровни ряда представлены как сумма трендовой (Т), сезонной или циклической (S) и случайной (Е) компонент:

    уt=Т+S+Е.

    Для того, чтобы построить аддитивную модель, для начала следует провести анализ структуры временного ряда, то есть определить наличие или отсутствие данных компонент в ряду динамики. Для определения структуруы временного ряда будем использовать автокорреляцию, заполнив вычислениями таблицы с 6 по 8.

    Таблица 6 – Вычисление автокорреляции для временного ряда с лагом 1

    t










    1
    1,3
    -
    -
    -
    -

    2
    1,4
    1,3
    1,96
    1,69
    1,82

    3
    1,5
    1,4
    2,25
    1,96
    2,10

    4
    1,7
    1,5
    2,89
    2,25
    2,55

    5
    2,1
    1,7
    4,41
    2,89
    3,57

    6
    2,2
    2,1
    4,84
    4,41
    4,62

    7
    2,5
    2,2
    6,25
    4,84
    5,50

    8
    2,7
    2,5
    7,29
    6,25
    6,75

    9
    3,0
    2,7
    9,00
    7,29
    8,10

    10
    3,3
    3,0
    10,89
    9,00
    9,90

    Итого Σ c 2 по 10
    20,4
    18,4
    49,78
    40,58
    44,91

    Среднее
    2,3
    2,0
    5,53
    4,51
    4,99

    Дисперсия
    0,393
    0,329
     
     
     

    Среднее кв. откл.
    0,627
    0,574
     
     
     

    Выведем коэффициент автокорреляции с лагом 1: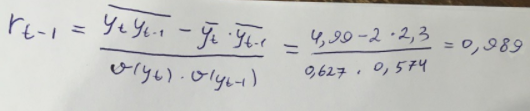



    Таблица 7 – Вычисление автокорреляции для временного ряда с лагом 2

    t










    1
    1,3
     -
    - 
    - 
    - 

    2
    1,4
     -
     -
     -
     -

    3
    1,5
    1,3
    2,25
    1,69
    1,95

    4
    1,7
    1,4
    2,89
    1,96
    2,38

    5
    2,1
    1,5
    4,41
    2,25
    3,15

    6
    2,2
    1,7
    4,84
    2,89
    3,74

    7
    2,5
    2,1
    6,25
    4,41
    5,25

    8
    2,7
    2,2
    7,29
    4,84
    5,94

    9
    3,0
    2,5
    9,00
    6,25
    7,50

    10
    3,3
    2,7
    10,89
    7,29
    8,91

    Итого Σ c 3 по 10
    19,0
    15,4
    47,82
    31,58
    38,82

    Среднее
    2,4
    1,9
    5,98
    3,95
    4,85

    Дисперсия
    0,337
    0,242
     
     
     

    Среднее кв. откл.
    0,580
    0,492
     
     
     
    1   2   3   4   5

    написать администратору сайта