Главная страница
Навигация по странице:

  • 32,904 28,858 1,0968

  • 0,0783 7,236 1,586

  • Стандартизированные коэффициенты регрессии имеют следующие значения

  • Далее произведем вычисление средних коэффициентов эластичности

  • Найдем значение множественного коэффициента корреляции

  • Теперь вычислим частные коэффициенты корреляции и оценим зависимость труда

  • Следующим шагом найдем общий F -критерий Фишера

  • Вычислим t -критерий Стьюдента для оценки параметра регрессии

  • Проведем анализ частных F-критериев Фишера

  • Модель парной линейной регрессии

    		•

    Эконометрика. Контрольная работа. 3 курс. Эконометрика. КР 3 курс. Контрольная работа по дисциплине Эконометрика Вариант 1 Содержание задача парная регрессия 2 задача множественная регрессия и корреляция 13


    Скачать 4.43 Mb.
    НазваниеКонтрольная работа по дисциплине Эконометрика Вариант 1 Содержание задача парная регрессия 2 задача множественная регрессия и корреляция 13
    АнкорЭконометрика. Контрольная работа. 3 курс
    Дата29.04.2023
    Размер4.43 Mb.
    Формат файлаdocx
    Имя файлаЭконометрика. КР 3 курс.docx
    ТипКонтрольная работа
    #1097643
    страница2 из 5
    1   2   3   4   5

    ЗАДАЧА 2. Множественная регрессия и корреляция


    Изучается зависимость показателя y от факторов х1 и х2.

    Требуется (длявсехвариантов):

    1. Построить линейную модель множественной регрессии. Записать стандартизованное уравнение множественной регрессии. На основе стандартизованных коэффициентов регрессии и средних коэффициентов эластичности ранжировать факторы по степени их влияния на результат.

    2. Найти коэффициенты парной, частной и множественной корреляции. Проанализировать их.

    3. С помощью F-критерия Фишера оценить статистическую надежность уравнения регрессии и коэффициента детерминации.

    4. С помощью частных F-критериев Фишера и t-статистики Стьюдента оценить целесообразность включения в уравнение множественной регрессии фактора х1 после х2 и фактора х2 после х1.

    5. По возможности составить уравнение линейной парной регрессии, оставив лишь один значащий фактор.

    y1
    9,4
    9,9
    9,1
    5,5
    6,6
    4,3
    7,4
    6,6
    5,5
    9,4
    5,7
    5,2
    10
    6,7

    x1
    0,23
    0,43
    0,26
    0,43
    0,38
    0,42
    0,3
    0,37
    0,34
    0,23
    0,41
    0,41
    0,22
    0,31

    x3
    0,4
    0,19
    0,44
    0,25
    0,02
    0,06
    0,15
    0,24
    0,11
    0,47
    0,2
    0,24
    0,54
    0,29




    y1
    Производительность труда, тыс. руб./чел.

    x1
    Трудоемкость единицы продукции

    x3
    Удельный вес покупных изделий

    (вариант 1)
    Составим сводную таблицу оценки зависимости производительности труда от трудоемкости продукции и удельного веса покупных изделий. Занесем данные в таблицу 5.

    Таблица 5 – Оценка зависимости производительности труда (у) от трудоемкости продукции (х1) и удельного веса покупных изделий (х2)

    №
    х1

    х2

    у

    х12
    х22
    у2
    х1∙у
    х2∙у
    х1∙х2




    1
    0,23
    0,40
    9,4
    0,0529
    0,1600
    88,36
    2,162
    3,760
    0,0920
    8,973
    0,182

    2
    0,43
    0,19
    9,9
    0,1849
    0,0361
    98,01
    4,257
    1,881
    0,0817
    6,063
    14,719

    3
    0,26
    0,44
    9,1
    0,0676
    0,1936
    82,81
    2,366
    4,004
    0,1144
    8,929
    0,029

    4
    0,43
    0,25
    5,5
    0,1849
    0,0625
    30,25
    2,365
    1,375
    0,1075
    6,392
    0,796

    5
    0,38
    0,02
    6,6
    0,1444
    0,0004
    43,56
    2,508
    0,132
    0,0076
    5,573
    1,056

    6
    0,42
    0,06
    4,3
    0,1764
    0,0036
    18,49
    1,806
    0,258
    0,0252
    5,440
    1,299

    7
    0,30
    0,15
    7,4
    0,0900
    0,0225
    54,76
    2,220
    1,110
    0,0450
    6,988
    0,169

    8
    0,37
    0,24
    6,6
    0,1369
    0,0576
    43,56
    2,442
    1,584
    0,0888
    6,865
    0,070

    9
    0,34
    0,11
    5,5
    0,1156
    0,0121
    30,25
    1,870
    0,605
    0,0374
    6,417
    0,842

    10
    0,23
    0,47
    9,4
    0,0529
    0,2209
    88,36
    2,162
    4,418
    0,1081
    9,357
    0,002

    11
    0,41
    0,20
    5,7
    0,1681
    0,0400
    32,49
    2,337
    1,140
    0,0820
    6,294
    0,353

    12
    0,41
    0,24
    5,2
    0,1681
    0,0576
    27,04
    2,132
    1,248
    0,0984
    6,513
    1,725

    13
    0,22
    0,54
    10,0
    0,0484
    0,2916
    100,00
    2,200
    5,400
    0,1188
    9,828
    0,030

    14
    0,31
    0,29
    6,7
    0,0961
    0,0841
    44,89
    2,077
    1,943
    0,0899
    7,667
    0,935

    Итого
    4,74
    3,60
    101,3
    1,6872
    1,2426
    782,83
    32,904
    28,858
    1,0968
    101,300
    22,206

    Среднее

    0,34
    0,26
    7,24
    0,1205
    0,0888
    55,92
    2,350
    2,061
    0,0783
    7,236
    1,586

    Найдем дисперсию: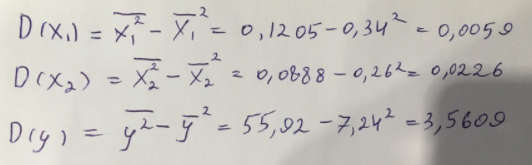



    Найдем среднеквадратическое отклонение: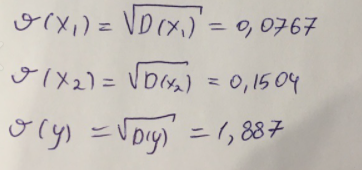



    Составим парные коэффициенты корреляции, сделав выводы об их зависимости: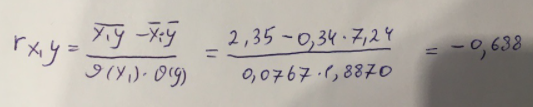



    Мы видим, что коэффициент корреляции по модулю сильно ближе к значению 1. Поэтому зависимость производительности труда (у) от трудоемкости продукции (х1) заметная, обратная.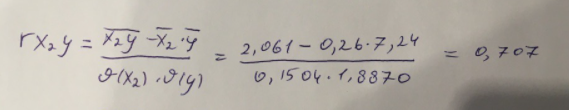



    Мы видим, что коэффициент корреляции по модулю близок к 1. Поэтому Зависимость производительности труда (у) от удельного веса покупных изделий (х2) тесная, прямая.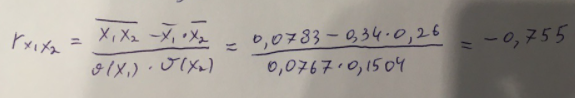


    Мы видим, что коэффициент корреляции по модулю близок к 1. Поэтому взаимосвязь между трудоемкостью продукции (х1) и удельным весом покупных изделий (х2) – тесная, обратная.

    Обычный вид уравнения множественной регрессии: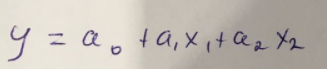



    Для расчета параметров линейного уравнения множественной регрессии будем использовать -коэффициенты (ибо упрощаются расчеты и не нет нужды использовать матричный метод для расчетов параметров уравнения регрессии):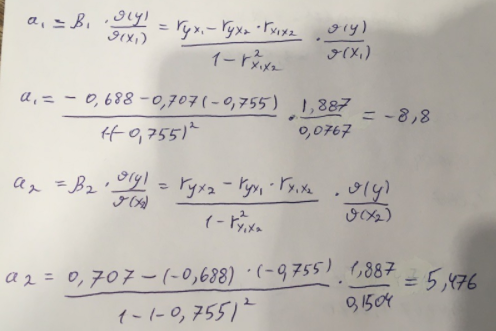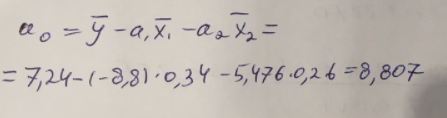





    Составим уравнение множественной регрессии в обычном виде: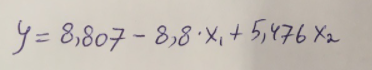



    Сделаем небольшие выводы по высчитанным параметрам. Параметр а1 позволяет нам увидеть, что с увеличением трудоемкости продукции (х1) на 1 ед. производительность труда (у) в среднем снизится на 8,800 тыс.руб./чел.

    Параметр уравнения а2 позволяет понять, что с увеличением удельного веса покупных изделий (х2) на 1 ед. производительность труда (у) в среднем вырастет на 5,476 тыс.руб./чел.

    Стандартизированные коэффициенты регрессии имеют следующие значения:



    Итогом по проделанным вычислениям будет следующее: при увеличении трудоемкости продукции (х1) на 1 от своей средней производительность труда (у) снизится на 0,358; а при увеличении удельного веса покупных изделий (х2) на 1  от своей средней производительность труда (у) вырастет на 0,437. Стоит заметить, что начения 1 и 2 по модулю очень близки.

    Далее произведем вычисление средних коэффициентов эластичности: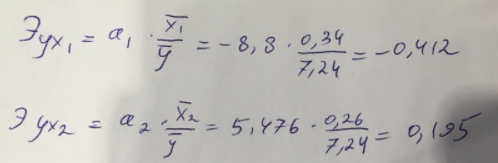


    Произведя вычисление частных коэффициентов эластичности можно с уверенностью сказать, что результат – производительность труда (у) – более эластичен к изменению трудоемкости продукции (х1) и менее – к изменению удельного веса покупных изделий (х2).

    Теперь приведем ранжирование факторов:

    Ранг 1 – удельный вес покупных изделий (х2) – больше β2 и r ух2.

    Ранг 2 – трудоемкость продукции (х1) – меньшее β1 и rух1.

    Найдем значение множественного коэффициента корреляции: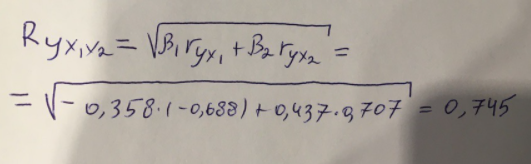



    Мы видим, что множественный коэффициент корреляции имеет значение выше 0,7, можно говорить о наличии тесной зависимости производительности труда (у) от двух факторов: трудоемкости продукции (х1) и удельного веса покупных изделий (х2).

    Теперь вычислим частные коэффициенты корреляции и оценим зависимость труда: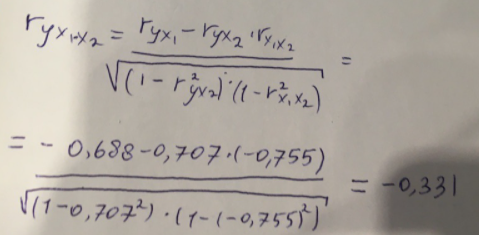



    Очевидно, что исключая влияние фактора х2 зависимость производительности труда (у) от трудоемкости продукции (х1) умеренная, обратная.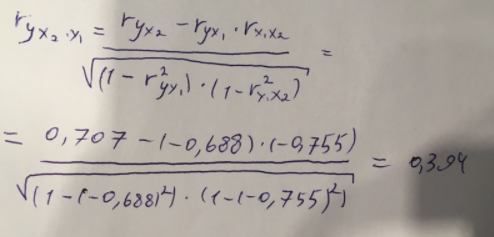



    Можно понять, что исключая влияние фактора х1 зависимость производительности труда (у) от удельного веса покупных изделий (х2) умеренная, прямая.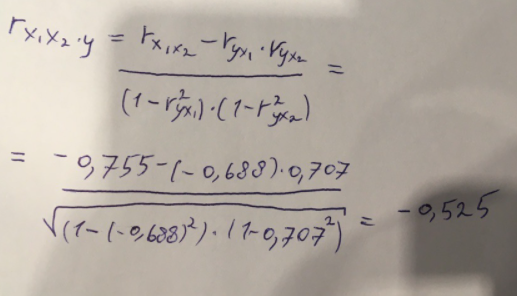



    Мы можем говорить о заметной связи факторов друг с другом, ибо коэффициент корреляции по модулю сильно отклоняется от значения 1 и от значения 0.

    Следующим шагом найдем общий F-критерий Фишера.

    Выдвигаем гипотезу: уравнение регрессии является статистически ненадежным.

    Фактическое значение F-критерия рассчитывается по формуле: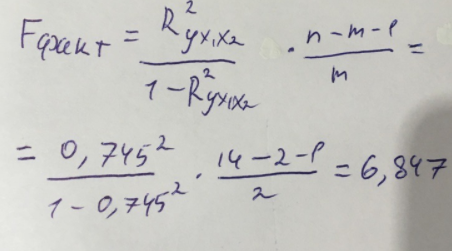



    Табличное значение F-критерия мы найдем по таблице Фишера по известным уровню значимости и степеням свободы:

     = 0,05 (уровень значимости);

    к1 = п – т – 1 = 14 – 2 – 1 = 11;

    к2 = т = 2

    Fтабл = 3,982

    Сравнивая фактическое и табличное значения F-критерия, получаем:

    Fфакт > Fтабл (6,847 > 3,982)

    Подытоживая мы убедились в гипотезе о том, что уравнение множественной регрессии является статистически ненадежным, не соответствуя при этом данным, ибо фактическое значение F-критерия превышает табличное т.е. уравнение множественной регрессии действительно является надежным и статистически значимым.
    t-критерий Стьюдента:

    Табличное значение t-критерия находится по таблице Стьюдента:

     = 0,05 (уровень значимости);

    df = п – 2 = 14 – 2 = 12 (число степеней свободы);

    tтабл = 2,179

    Вычислим t-критерий Стьюдента для оценки параметра регрессии а1:

    Выдвигаем гипотезу: параметр регрессии а1 имеет случайный характер и а1=0.

    Фактическое значение t-критерия рассчитывается по формуле: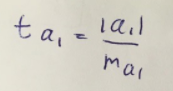

    где т - стандартная ошибка параметра а1



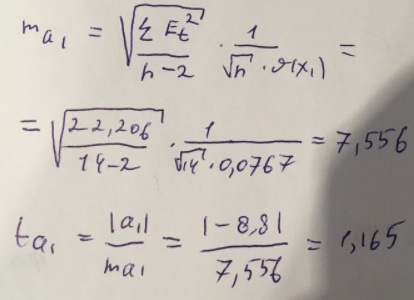    Сравнивая фактическое и табличное значения t-критерия, получаем:

    tфакт< tтабл (1,165 < 2,179)

    Проанализируем итоги вычислений. Мы видим, что выдвинутая гипотеза о том, что параметр регрессии а1 имеет случайный характер и равен нулю, соответствует данным. Поэтому параметр а1 уравнения парной регрессии не является статистически незначимым.

    Вычислим t-критерий Стьюдента для оценки параметра регрессии а2:

    Выдвигаем гипотезу: параметр регрессии а2 имеет случайный характер и а2=0.

    Фактическое значение t-критерия рассчитывается по формуле: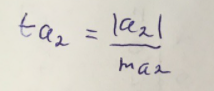

    где т - стандартная ошибка параметра а2



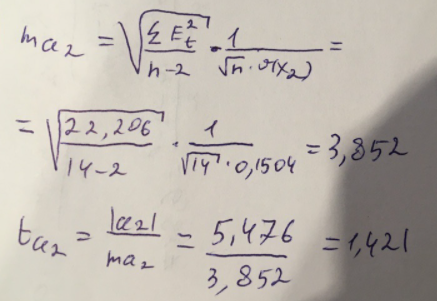    Сравнивая фактическое и табличное значения t-критерия, получаем:

    tфакт< tтабл (1,421< 2,179)

    Итогом для нас будет следующее: выдвинутая гипотеза о том, что параметр регрессии а2 имеет случайный характер и равен нулю, соответствует данным. Поэтому параметр а2 уравнения парной регрессии не является статистически незначимым.

    Проведем анализ частных F-критериев Фишера:

    Выдвигаем гипотезу №1: фактор х1 из модели можно исключить.

    Фактическое значение F-критерия рассчитывается по формуле: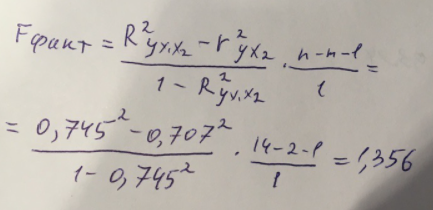



    Сравнивая фактическое и табличное значения F-критерия, получаем:

    Fфакт < Fтабл (1,356 < 3,982)

    Мы подтвердили гипотезу о том, что фактор х1 из модели можно исключить, т.е. влияние фактора х1 на результат при наличии в модели фактора х2 не является значимым.

    Выдвигаем гипотезу №2: фактор х2 из модели можно исключить.

    Фактическое значение F-критерия рассчитывается по формуле: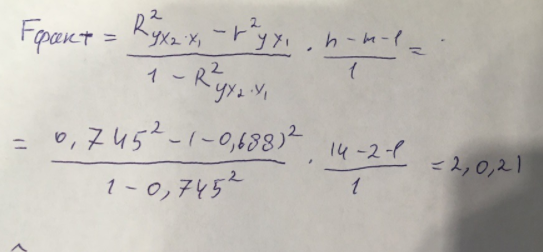



    Сравнивая фактическое и табличное значения F-критерия, получаем:

    Fфакт < Fтабл (2,021 < 3,982)

    Мы подтвердили гипотезу о том, что фактор х2 из модели можно исключить верна, т.е. влияние фактора х2 на результат при наличии в модели фактора х1 не является значимым.

    Итогом для нас будет следующее: мы поняли, что наименьшее значение частного F-критерия Фишера у фактора х1, поэтому исключим именно его из расчетов.

    Модель парной линейной регрессии:

    В общем виде линейное уравнение парной регрессии выглядит следующим образом: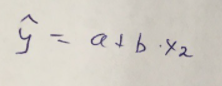



    Используем метод наименьших квадратов для нахождения необходимых параметров: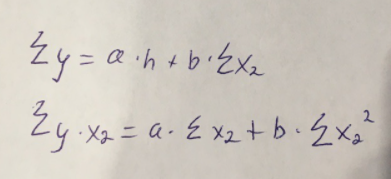



    Вычислим параметры: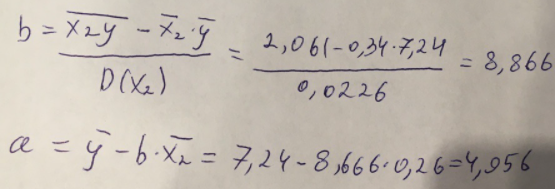



    Линейное уравнение парной регрессии будет выглядеть так: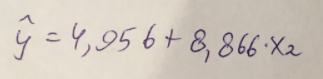



    По расчетам мы делаем вывод о параметре уравнения b, который показывает, что с увеличением удельного веса покупных изделий (х2) на 1 ед. производительность труда (у) в среднем вырастет на 8,866 тыс.руб./чел.
    1   2   3   4   5

    написать администратору сайта