лаб 6к. Лабораторная работа м 6к изучение свободных механических колебаний математического маятника цель работы
 Скачать 1.34 Mb. Скачать 1.34 Mb.
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| | (1) |
В уравнении (1) зависящая от времени функция x = x(t) может быть и координатой шарика, колеблющегося на пружине, и углом отклонения физического или математического маятника от положения равновесия, и током в колебательном контуре, если речь идет об электромагнитных колебаниях. В механических системах уравнение вида (1) возникает тогда, когда, во-первых, в системе не действуют силы трения и другие диссипативные силы, а во-вторых, на тело, выведенное из положения равновесия, действует возвращающая сила, прямо пропорциональная отклонению тела от положения равновесия. Вывод уравнения (1) приведено ниже на примере математического маятника.
Решением уравнения (1) являются гармонические функции и колебания величины Х описываются уравнениями типа
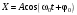 или или 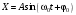 . . | (2) |
На рис.1 представлены графики зависимости смещения Х и потенциальной энергии Eп (при Eп X2) от времени для материальной точки, колеблющейся по гармоническому закону
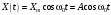 (при условии, что φ0 = 0). Колебания совершаются около положения равновесия, отвечающего значению Х =0.
(при условии, что φ0 = 0). Колебания совершаются около положения равновесия, отвечающего значению Х =0.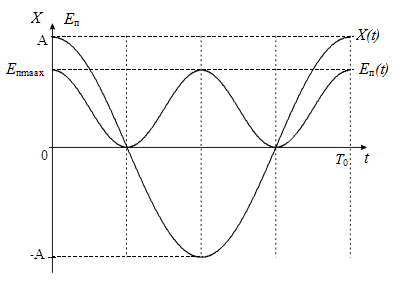
Рис.1. Зависимости смещения Х ипотенциальной энергии Еп от времени при гармонических колебаниях.
Поскольку величина косинуса изменяется в пределах от –1 до +1, то значения Х лежат в пределах от – А до +А, где А – это амплитуда колебаний – величина наибольшего отклонения колеблющейся величины Х от положения равновесия.
Аргумент косинуса – величина (ω0 t + φ0) называется фазой колебаний. Постоянная величина φ0представляет собой значение фазы в момент времени t= 0 и называется начальной фазой колебаний. С изменением начала отсчета времени изменяется и начальная фаза колебаний. Следовательно, значение начальной фазы определяется выбором начала отсчета времени. Так как величина Х не изменяется при добавлении или вычитании из фазы целого числа 2π, то всегда можно добиться того, чтобы начальная фаза была по модулю меньше π. Поэтому обычно рассматриваются только значения начальной фазы колебаний φ0, лежащие в пределах от –π до +π.
Поскольку косинус (синус) – периодическая функция с периодом 2π, различные состояния системы, совершающей гармонические колебания, повторяются через такой промежуток времени, за который фаза колебаний получает приращение, равное
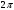 (см. рис.1)
(см. рис.1) 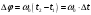 ; если ; если 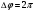 . то . то 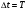 . . | (3) |
Период гармонического колебанияT – это такой промежуток времени, за который фаза колебаний получает приращение, равное 2π, т.е. совершаетсяодно полное колебание. По истечении времени, соответствующего периоду колебания, изменяющаяся величина принимает своё прежнее значение (рис.1). Следовательно, период колебания определяется из равенства
[ω0 (t+T) + φ0]– (ω0 t + φ0) = 2
 ,
,откуда
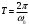 . . | (4) |
Величина
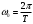
называетсясобственной циклической частотой гармонических колебаний и измеряется в СИ в рад/с.
Частота колебаний ν – это величина, которая равна числу полных колебаний N в единицу времени; эта величина, обратная периоду колебаний
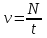 или или 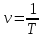 . . | (5) |
Единица измерения частотывСИ – герц (Гц).
Сравнивая равенства (4) и (5), получаем формулу вычисления
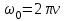 . . | (6) |
В качестве примера колебательного движения, поясняющего физические условия, при которых совершаются гармонические колебания, может служить движение математического маятника.
Математическим маятником называют идеализированную систему, состоящую из невесомой и нерастяжимой нити, на одном конце которой прикреплена масса, сосредоточенная в одной точке. Хорошим приближением математического маятника является небольшой тяжелый шарик массой m, подвешенный на нити длиной ℓ, и колеблющаяся под действием силы тяжести.
Если маятник отклонить от положения равновесия на небольшой угол φ (φ – угол, образованный нитью с вертикалью) и отпустить его, то маятник начнет совершать колебательное движение (рис. 2).
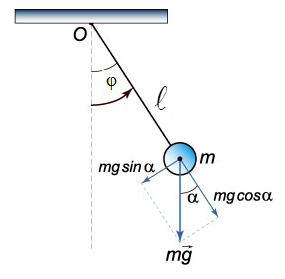
Рис.2. Движение математического маятника.
При отклонении маятника из положения равновесия возникает вращательный момент силы тяжести
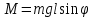 , который заставляет систему вернуться в состояние равновесия. Тогда, в отсутствии сил сопротивления с учетом того, что момент силы натяжения нити относительно точки О равен нулю, основной закон динамики вращательного движения твердого тела вокруг неподвижной оси можем написать в виде
, который заставляет систему вернуться в состояние равновесия. Тогда, в отсутствии сил сопротивления с учетом того, что момент силы натяжения нити относительно точки О равен нулю, основной закон динамики вращательного движения твердого тела вокруг неподвижной оси можем написать в виде 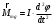 . . | (7) |
Обозначив угловое ускорение через
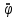 и учитывая, что момент инерции материальной точки равен
и учитывая, что момент инерции материальной точки равен 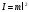 , перепишем уравнение (7) в проекции на ось, проходящую через точку подвеса перпендикулярно рисунку и направленную от чертежа к нам, в виде:
, перепишем уравнение (7) в проекции на ось, проходящую через точку подвеса перпендикулярно рисунку и направленную от чертежа к нам, в виде: 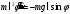 . . | (8) |
При малых углах отклонения sinφ можно заменить углом φ (в радианах), тогда, обозначив
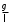 через ω02, уравнение (8) можно записать следующим образом:
через ω02, уравнение (8) можно записать следующим образом: 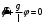 или или  . . | (9) |
Решением этого уравнения является функция
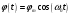 , , | (10) |
где
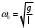 | (11) |
– собственная циклическая частота колебаний математического маятника.
Из выражения (11) вытекает, что собственная циклическая частота колебаний математического маятника зависит только от длины маятника и ускорения свободного падения. Учитывая связь между собственной циклической частотой математического маятника и периодом колебаний, получаем формулу вычисления периода колебаний математического маятника
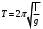 . . | (12) |
4. Методика виртуального эксперимента
В данной лабораторной работе используется компьютерная модель, основанная на решении (10) дифференциального уравнения гармонического колебания.
Откройте компьютерную модель «Свободные механические колебания». Внимательно рассмотрите модель, найдите все регуляторы и другие основные элементы.
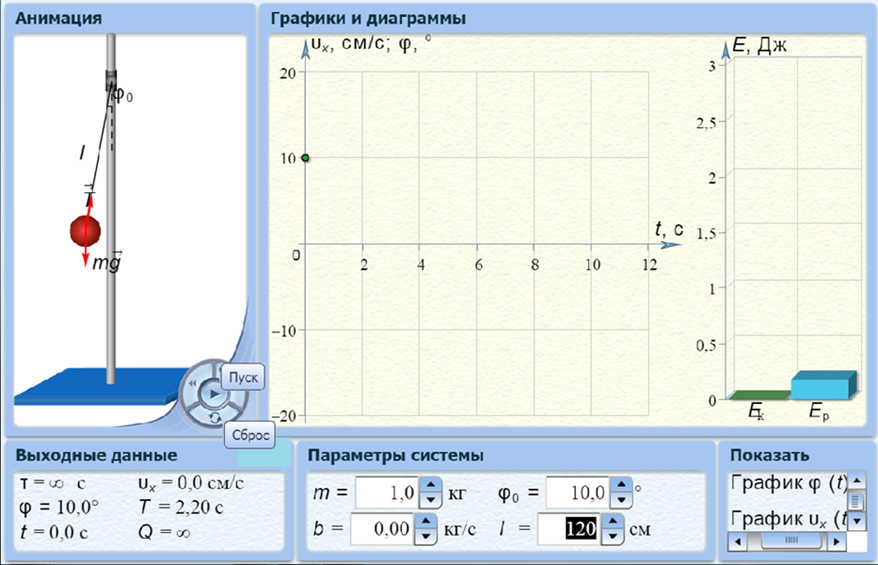
Рис.3. Диалоговое окно компьютерной модели «Математический маятник»
в режиме «Сброс» (отдельно показано обозначения кнопки управления режима «Пуск»).
Компьютерная модель «Математический маятник» позволяет устанавливать значения массы m шарика, подвешенного на нити, длина ℓ которой также регулируется, угол отклонения φ0 нити от положения равновесия шарика и вязкость b среды колебаний шарика регуляторами соответствующих величин, расположенными справа внизу диалогового окна модели и обозначенными как «Параметры системы» (рис.3).
В модели есть кнопка управления, которой задают режимы модели. Щелкнув мышью по кнопке «Сброс» (нижняя часть кнопки управления), задают параметры величин для виртуального эксперимента. Запускают виртуальный эксперимент кнопкой «Пуск» (средняя часть кнопки управления). Кнопкой «Пауза» (средняя часть кнопки управления, проявляющаяся при режиме «Пуск») останавливают эксперимент (рис.4). Возвращаются к ранее заданным параметрам величин виртуального эксперимента кнопкой «Сброс» после нажатия кнопки «ОК» в появляющемся окошке «Анимация закончилась» по завершении виртуального эксперимента (колебания в модели ограничены числом 6).
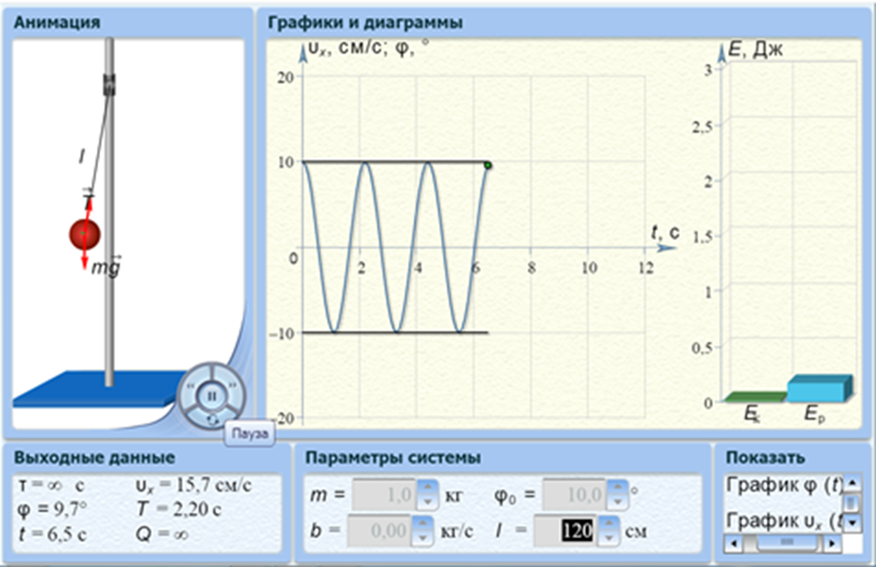
Рис.4. Диалоговое окно компьютерной модели «Математический маятник»
в режиме «Пауза».
В отдельном блоке модели «Выходные данные» фиксируются значения параметров системы в любой момент времени, в том числе угол отклонения φ,0 в момент времени t,c колебания.
Меткой выбирают график, который необходимо показать – это может быть φ (t), или Uх(t), или оба графика одновременно.
Модель графически показывает значения потенциальной Ер и кинетической Ек энергий маятника.
Переписав формулу (12) в виде
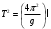 , , | (13) |
можно сделать вывод, что квадрат периода колебаний Т2 математического маятника линейно зависит от длины нити ℓ, что позволяет по тангенсу угла наклона графика зависимости квадрата периода колебаний маятника от величины длины нити экспериментально определить значение ускорения свободного падения g, используя формулу
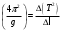 , , | (14) |
где ∆(Т2) – это приращение функции при соответствующем приращении аргумента∆ℓ. Из этой формулы получаем формулу вычисления ускорения свободного падения
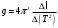 , , | (15) |
5. Порядок выполнения работы
Эксперимент 1. Исследование закономерностей свободных колебаний математического маятника
1. Запустите виртуальный эксперимент «Математический маятник»
2. В режиме «Сброс» установите метку " график φ(t) ".
3. С помощью движков регуляторов установите значение коэффициента вязкости среды b = 0 кг/с.
4. Установите значение начального угла φ0 = 100, длину нити ℓ = 130см и массу шарика m = 1,0 кг.
5. Кнопкой «Пуск» запустите эксперимент, наблюдайте за значениями потенциальной Ер и кинетической Ек энергий маятника в процессе колебания и зафиксируйте значение периода колебаний в табл. 1.
6. Вернитесь в режим «Сброс», установите массу шарика m = 2,0 кг и, не изменяя значения начального угла и длину нити, повторите пункт 5.
7. Повторите пункты 6 и 5 с массой m = 3,0 кг.
8. В режиме «Сброс» установите массу шарика m = 1,0 кг, длину нити ℓ = 120 см и значение начального угла φ0 = 100.
9. Кнопкой «Пуск» запустите эксперимент, наблюдайте за значениями потенциальной Ер и кинетической Ек энергий маятника в процессе колебания и зафиксируйте значение периода колебаний в табл. 1.
10. Вернитесь в режим «Сброс», установите значение начального угла φ0 = 150 и, не изменяя значения массы и длину нити, повторите пункт 9.
11. Выполните эксперимент (пункт 10) для φ0 = 200.
12. В режиме «Сброс» установите массу шарика m = 1,0 кг, значение начального угла φ0 = 200 и длину нити ℓ = 90 см.
13. Кнопкой «Пуск» запустите эксперимент, наблюдайте за значениями потенциальной Ер и кинетической Ек энергий маятника в процессе колебания и зафиксируйте значение периода колебаний в табл. 1.
14. Вернитесь в режим «Сброс», установите длину нити ℓ = 110 см и, не изменяя значения массы и начального угла φ0, повторите пункт 13.
15. Выполните эксперимент (пункт 14) для ℓ = 130 см.
Таблица 1
Результаты измерений периода колебаний
| φ0 =100; ℓ = 130 см | m = 1,0 кг; ℓ = 120 см | m = 1,0 кг; φ0 = 200 | ||||
| m, кг | Т, с | φ0, град | Т, с | ℓ, см | Т, с | |
| 1,0 | | 10 | | 90 | | |
| 2,0 | | 15 | | 110 | | |
| 3,0 | | 20 | | 130 | | |
Эксперимент 2. Определение ускорения свободного падения
1. Запустите виртуальный эксперимент «Математический маятник»
2. В режиме «Сброс» установите метку " график φ(t) ".
3. С помощью движков регуляторов установите значение коэффициента вязкости среды b = 0 кг/с, максимальную длину нити ℓ и значение начального угла φ0, указанное в табл. 2 для вашего варианта ((для определения номера варианта см. *ссылку в конце текста лабораторной работы).
4. Нажимая мышью на кнопку «Пуск», следите за движением точки на графике зависимости угла отклонения φ от времени и за поведением маятника. Потренируйтесь, останавливая движение кнопкой «Пауза» (например, в максимуме смещения точки от положения равновесия) и запуская далее кнопкой «Пуск». Выберите число полных колебаний N = 3, 4 или 5 и измеряйте их продолжительность t (как разность времени колебания t2 – t1, фиксируемого в блоке «Выходные данные», где t1 и t2 - значение времени t в момент начала и конца отсчета колебаний). Возможно брать t1 = 0, тогда t будет равно значению времени t в конце колебаний, как показано на рис.4 для 3 колебаний). Результат измерения длительности колебаний t запишите в табл.3.
5. В режиме «Сброс» установите длину нити ℓ на 10 см меньше предыдущей и повторите измерения пункта 4.
6. Уменьшая длину нити ℓ каждый раз на 10 см (до минимальной длины 90 см), повторите пункт 5.
Таблица 2.
Значения начального угла отклонения (не перерисовывать).
| Вариант | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| φ0, град | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
Таблица 3.
Определение ускорения свободного падения
| N = | |||||
| ℓ, м | t1, с | t2, с | ∆t, с | T, с | T2, с2 |
| | | | | | |
| | | | | | |
| | | | | | |
| | | | | | |
| | | | | | |
Обработка результатов измерений
Эксперимент 1.
Проанализируйте результаты наблюдений и измерений (табл.1) и сделайте выводы:
1. Как влияет изменение массы шарика, угла отклонения и длины нити на величину периода колебаний математического маятника?
2. Как влияет увеличение массы шарика, угла отклонения и длины нити на величину потенциальной энергии математического маятника?
Эксперимент 2.
1. Вычислите период колебаний по формуле (
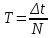 ), квадрат периода и заполните табл. 3 .
), квадрат периода и заполните табл. 3 .2. Постройте график зависимости квадрата периода колебаний математического маятника от его длины нити Т2 = f(ℓ).
3. Из графика Т2 = f(ℓ)определите значение ускорения свободного падения g, используя формулу (15), где
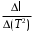 – этоотношение изменения длины математического маятника к соответствующему изменению квадрата периода колебаний этого маятника.Оцените ошибку определения ∆g ускорения свободного падения (см. Приложение).
– этоотношение изменения длины математического маятника к соответствующему изменению квадрата периода колебаний этого маятника.Оцените ошибку определения ∆g ускорения свободного падения (см. Приложение).4. Запишите ответ, сравнив его с табличным значением.
7. Вопросы для подготовки к допуску
Что называют колебаниями; механическими колебаниями; свободными колебаниями?
Приведите примеры свободных колебаний.
Нарисуйте на одном листе графики двух гармонических колебаний одинаковой частоты, разность фаз которых составляет π.
Амплитуда гармонического колебания увеличилась в два раза. Как при этом изменяются период колебания и максимальная скорость?
Два математических маятника, длины которых отличаются на
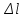 = 16см, совершают за одно и тоже время один N1 = 10 колебаний, а другой N2 = 30 колебаний. Определить длины маятников.
= 16см, совершают за одно и тоже время один N1 = 10 колебаний, а другой N2 = 30 колебаний. Определить длины маятников.Тонкий однородный стержень длиной 1 м может свободно вращаться вокруг горизонтальной оси, отстоящей на расстоянии 20 см от его середины. Определите период колебаний стержня, считая колебания гармоническими.
К пружине подвесили грузик, в результате чего статическая деформация пружины составила 9 см. Каков будет период гармонических колебаний грузика, если систему вывести из состояния равновесия?
8. Литература
Трофимова Т.И. Курс физики. - М.: издательский центр "Академия" (или другие издательства), 2012 – 2020 г.г.
Савельев И.В. Курс общей физики. Том 1. Механика. Молекулярная физика. – Спб.: Лань (или другие издательства), 2012 – 2020 г.г.
*Как определить номер варианта при выполнении
лабораторной работы
| Номер (по списку группы) | 1, 11, 21, 31 | 2, 12, 22, 32 | 3, 13, 23 | 4, 14, 24 | 5, 15, 25 | 6, 16, 26 | 7, 17, 27 | 8, 18, 28 | 9, 19, 29 | 10, 20, 30 |
| Вариант | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Приложение
ЛР М-6к «Изучение свободных механических колебаний математического маятника»
Обработка результатов эксперимента
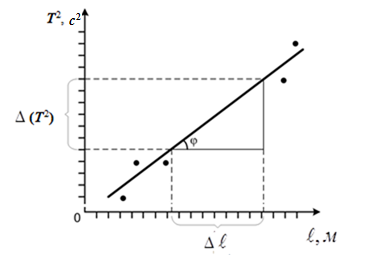
При обработке результатов эксперимента используют метод определения постоянной величины из графика линейной функции
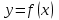 в случае, если постоянная величина k является коэффициентом наклона графика этой зависимости, т.е. когда
в случае, если постоянная величина k является коэффициентом наклона графика этой зависимости, т.е. когда 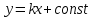 . (1)
. (1)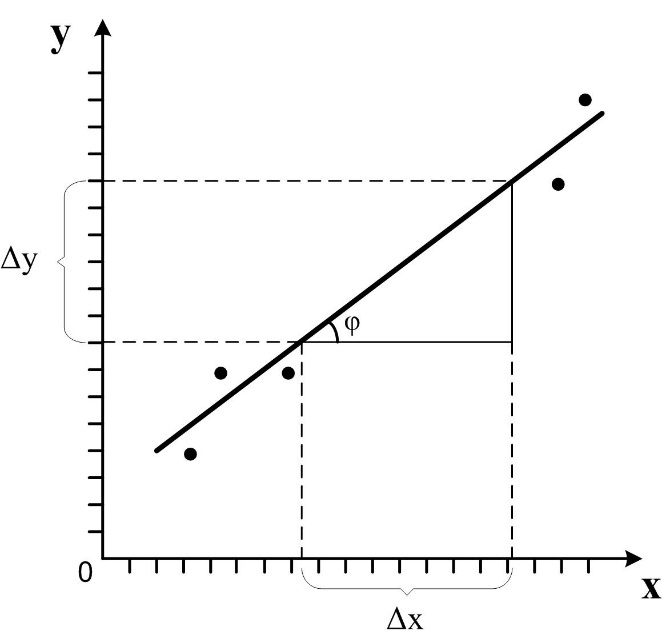
Рис. График линейной функции
 .
.Используя экспериментальные данные, отмечают их точками (при однократных измерениях, или отмечают область возможных значение при многократных измерениях) в системе координат YOX и проводят прямую с некоторой достоверностью, если точки не лежат точно по прямой, или прямо по экспериментальным точкам, если они укладываются в прямую. Далее отмечают в средней части этой прямой область, граничные точки которой дают в проекции на оси абсцисс и ординат численные значения интервалов ∆x и ∆y, по которым вычисляют постоянную величинуk по формуле
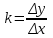 (2)
(2)где
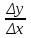 - это отношение приращения функции к соответствующему приращению аргумента.
- это отношение приращения функции к соответствующему приращению аргумента.Иногда в литературе такой метод определения постоянной величиныk излагают как метод определения постоянной величины по тангенсу угла наклона линейной функции к оси абсцисс. Действительно, из рисунка видно, что отношение
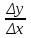 - это отношение противолежащего катета угла φ к прилежащему катету этого угла, что является тангенсом угла φ, т.е.
- это отношение противолежащего катета угла φ к прилежащему катету этого угла, что является тангенсом угла φ, т.е.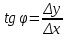 . (3)
. (3)При такой методике определения постоянной величины угол φ также необходимо отмечать в средней части прямой линии.
Аналогичные рассуждения проводят для определения величины ускорения свободного падения в лабораторной работе М-6к «Изучение свободных механических колебаний математического маятника», получая формулу вычисления
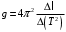
 , (4)
, (4)где ∆ℓ – отношение изменения длины математического маятника к соответствующему изменению квадрата периода колебаний ∆(Т2) этого маятника.
По экспериментальным данным строят график зависимости квадрата периода колебаний математического маятника от его длины нити Т2 = f(ℓ), выбирая соответствующий масштаб величин по осям.
Точность измерений характеризует относительная погрешность δ, которая показывает, во сколько раз величина погрешности ∆Х определения величины Хотличается от самой величины Xи; относительная погрешность
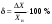 .
.Точность косвенных измерений величины ускорения свободного падения определяется равенством
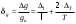 , (5)
, (5)где погрешности определения длины ∆ℓ и периода ∆Т только приборные, так как для каждой избранной величины длины ℓ определяется соответствующее значение периода Т только один раз (поэтому случайную ошибку определить невозможно). Из всех возможных значений δg необходимо брать наибольшее, поэтому выбирается минимальное значение длины ℓmin и соответствующее ему значение периода, которой тоже будет минимальным Тmin.
Из равенства (5) получаем формулу вычисления погрешности определения ускорения свободного падения
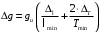 , (6)
, (6)в которую подставляем вычисленное по формуле (4) ускорение свободного падения, минимальное значение длины ℓmin и соответствующее ему значение периода, которой тоже будет минимальным Тmin., принимая
∆ℓ = 0,01м и ∆Т = 0,01с.
Результат определения ускорение свободного падения записывают в виде
 g = (gи ± ∆ g) м/с2
g = (gи ± ∆ g) м/с2