Лабораторная работа по дисциплине 1 Численные методы механики жидкости и газа Обработка результатов cfdэксперимента
 Скачать 185.1 Kb. Скачать 185.1 Kb.
|
|
Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение Высшего профессионального образования Новосибирский Государственный Технический Университет Кафедра Аэрогидродинамики Лабораторная работа по дисциплине №1 «Численные методы механики жидкости и газа» «Обработка результатов CFD-эксперимента» Вариант 3 Студент: Преподаватель: Факультет: ЛА Гостеев Ю.А. Группа: СА-71 Алпацкий Н.С. Новосибирск 2020 1.Задание: Обработать результаты расчета течения в каверне: - построить изолинии модуля скорости 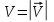 и компонент скорости 𝑢 и v, линии тока, поле векторов скорости; и компонент скорости 𝑢 и v, линии тока, поле векторов скорости; - для заданной стенки построить графики 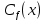 ( (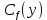 и и 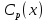 ( (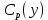 ); ); - определить действующие на заданную стенку силы и их коэффициенты. Схема течения приведена на рисунке 1. Скорость верхней стенки 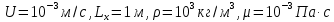 , число узлов сетки , число узлов сетки 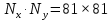 , , 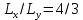 , стенка - правая. , стенка - правая.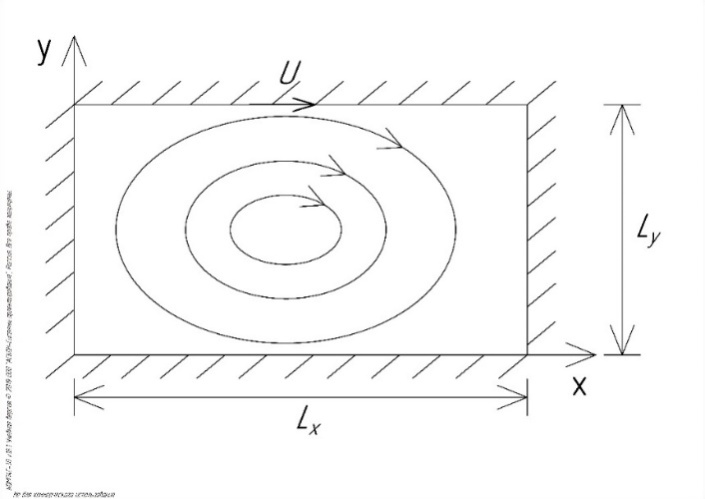 Рис. 1 2.Используемые формулы и алгоритм: Пусть в узлах 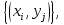 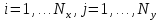 равномерной разностной сетки задано поле скоростей равномерной разностной сетки задано поле скоростей 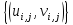 несжимаемого вязкого течения. несжимаемого вязкого течения.Тогда можно определить: - касательное напряжение на верхней стенке 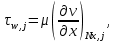 где 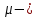 динамическая вязкость жидкости; динамическая вязкость жидкости;- давление на стенке 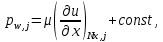 - коэффициент трения 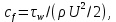 где 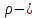 плотность жидкости, плотность жидкости, 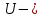 характерная скорость; характерная скорость;- коэффициент давления 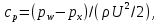 где 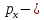 характерное давление; характерное давление;- действующие на стенку силы трения и давления 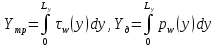 и их коэффициенты 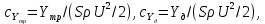 где 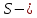 характерная площадь. характерная площадь.Для расчета значений частных производных на правой стенке используются несимметричные формулы конечных разностей: 1-го порядка 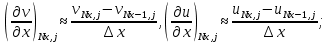 2-го порядка 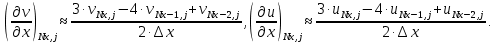 Для расчета интегралов – формулы численного интегрирования, например, формула трапеций. 3.Решение: Для правой стенки определим касательные напряжения, давления и распределение местного коэффициента трения и давления. Текст цикла: do j=1,Ny tao(j)=myu*(v(Nx,i)-v(Nx,i-1))/delx cf(j)=tao(j)/(po*Ubig**2/2) pw(j)=myu*(u(Nx,j)-u(Nx-1,j))/delx cp(j)=pw(j)/(po*Ubig**2/2) enddo Используя формулу трапеций, вычислим интегралы от касательных напряжений и давлений для нахождения силы трения и давления: Текстметода: b=0 s=0 do j=2,Ny-1 b=b+tao(j) s=s+pw(j) enddo Xtr=dely*((tao(1)+tao(Ny))/2+b) Xd=dely*((pw(1)+pw(Ny))/2+s) print*,'Xtr=',Xtr print*,'Xd=',Xd CXtr=Xtr/(Lz*Ly*po*Ubig**2/2) CXd=Xd/(Lz*Ly*po*Ubig**2/2) print*,'CXtr=',CXtr print*,'CXd=',CXd 4.Текст программы: program POST1 use GrafLib implicit real*8(a-h,o-z) parameter(nc=5,Npl=21) dimension z(nc),xpl(Npl),ypl(Npl),tao(81),cf(81),pw(81),cp(81) real*8 myu,Lx,Ly,Lz allocatable:: x(:),y(:),u(:,:),v(:,:) Lx=1.0 Ly=4/3. Lz=1.0 Ubig=1e-3 dely=0.0167 delx=0.0125 myu=1e-3 po=1e3 open(10,file='input.txt') open(10,file='var10.txt') read(10,*)Nx,Ny allocate(x(Nx),y(Ny),u(Nx,Ny),v(Nx,Ny)) read(10,*)x read(10,*)y read(10,*)(u(:,j),j=1,Ny) read(10,*)(v(:,j),j=1,Ny) aLmax=dmax1(x(Nx),y(Ny)) print*,'Flow statistics:' xmin=x(1) ;print*,' xmin=',xmin xmax=x(Nx);print*,' xmax=',xmax ymin=y(1) ;print*,' ymin=',ymin ymax=y(Ny);print*,' ymax=',ymax umin=minval(u);print*,' umin=',umin umax=maxval(u);print*,' umax=',umax vmin=minval(v);print*,' vmin=',vmin vmax=maxval(v);print*,' vmax=',vmax xgmin=0.; xgmax=aLmax ygmin=0.; ygmax=aLmax call GRAFINIT(1,'Contours') ii=clickmenuqq(QWIN$TILE) call PLOT2((/0.0d0,xmax,xmax,0.0d0,0.0d0/), & (/0.0d0,0.0d0,ymax,ymax,0.0d0/),0,1000,2d-3) Vmax=maxval(sqrt(u**2+v**2)) z=Vmax*dble((/0.1,0.2,0.4,0.8,0.99/)) call CPLOT(sqrt(u**2+v**2),1,Nx,1,Ny,x,y,nc,z) !z=dble((/-0.3,0.0,0.2,0.6,1.0/)) !call CPLOT(u,1,Nx,1,Ny,x,y,nc,z) !z=dble((/-0.4,-0.2,-0.1,0.05,0.17/)) !call CPLOT(v,1,Nx,1,Ny,x,y,nc,z) ii=SAVEIMAGE_W('contours.bmp',& xgmin-0.1,ygmax+0.1,xgmax+0.1,ygmin-0.1) call GrafInit(2,'Velocity Vectors') ii=clickmenuqq(QWIN$TILE) ig=setactiveqq(2) call PLOT2((/0.0d0,xmax,xmax,0.0d0,0.0d0/), & (/0.0d0,0.0d0,ymax,ymax,0.0d0/),0,1000,2d-3) call Vectors1(Nx,Ny,x,y,u,v,0.04d0,1,3,1d-3,1) ii=SAVEIMAGE_W('vectors.bmp',xgmin,ygmax,xgmax,ygmin) call GrafInit(3,'Pathlines') ii=clickmenuqq(QWIN$TILE) ig=setactiveqq(3) call PLOT2((/0.0d0,xmax,xmax,0.0d0,0.0d0/), & (/0.0d0,0.0d0,ymax,ymax,0.0d0/),0,1000,2d-3) xpl=0.5*xmax do j=1,Npl; ypl(j)=ymin+(j-1)*(ymax-ymin)/(Npl-1); end do !do i=1,Npl; xpl(i)=xmin+(i-1)*(xmax-xmin)/(Npl-1); end do call PLINES(Nx,Ny,x,y,u,v,Npl,xpl,ypl,1d-2,10000) ii=SAVEIMAGE_W('plines.bmp',xgmin,ygmax,xgmax,ygmin) u=u*Ubig v=v*Ubig do j=1,Ny tao(j)=myu*(v(Nx,j)-v(Nx-1,j))/delx cf(j)=tao(j)/(po*Ubig**2/2) pw(j)=myu*(u(Nx,j)-u(Nx-1,j))/delx cp(j)=pw(j)/(po*Ubig**2/2) enddo !print*,'tao=',tao !print*,'cf=',cf !print*,'pw=',pw print*,'cp=',cp b=0 s=0 do j=2,Ny-1 b=b+tao(j) s=s+pw(j) enddo Xtr=dely*((tao(1)+tao(Ny))/2+b) Xd=dely*((pw(1)+pw(Ny))/2+s) print*,'Xtr=',Xtr print*,'Xd=',Xd CXtr=Xtr/(Lz*Ly*po*Ubig**2/2) CXd=Xd/(Lz*Ly*po*Ubig**2/2) print*,'CXtr=',CXtr print*,'CXd=',CXd pause end logical function SOLID(x,y) implicit real*8(a-h,o-z) SOLID=.false. !if((x>=0.5).and.(y>=0.3))SOLID=.true. End subroutine CPLOT(d,ilb,iub,jlb,jub,x,y,nc,z) real*8 d(ilb:iub,jlb:jub) real*8 x(ilb:iub) real*8 y(jlb:jub) real*8 z(1:nc) real*8 h(0:4),x1,x2,y1,y2 integer sh(0:4) real*8 xh(0:4),yh(0:4) integer im(1:4),jm(1:4) integer cas integer castab(-1:1,-1:1,-1:1) integer p1,p2; logical SOLID data im/0,1,1,0/ data jm/0,0,1,1/ data castab/0,0,9, 0,1,5, 7,4,8, & 0,3,6, 2,3,2, 6,3,0, & 8,4,7, 5,1,0, 9,0,0/ xsect(p1,p2) = (h(p2)*xh(p1)-h(p1)*xh(p2))/(h(p2)-h(p1)) ysect(p1,p2) = (h(p2)*yh(p1)-h(p1)*yh(p2))/(h(p2)-h(p1)) 20 do 100 j=jub-1,jlb,-1 do 90 i=ilb,iub-1 dmin = min(d(i,j),d(i,j+1),d(i+1,j),d(i+1,j+1)) dmax = max(d(i,j),d(i,j+1),d(i+1,j),d(i+1,j+1)) if (dmax.ge.z(1) .and. dmin.le.z(nc)) then do 80 k=1,nc if (z(k).ge.dmin .and. z(k).le.dmax) then do 22 m=4,0,-1 if (m.gt.0) then h(m)=d(i+im(m),j+jm(m))-z(k) xh(m)=x(i+im(m)) yh(m)=y(j+jm(m)) else h(0)=0.25*(h(1)+h(2)+h(3)+h(4)) xh(0)=0.5*(x(i)+x(i+1)) yh(0)=0.5*(y(j)+y(j+1)) endif if (h(m).gt.0.0) then sh(m)=+1 else if (h(m).lt.0.0) then sh(m)=-1 else sh(m)=0 endif 22continue do 60 m=1,4 m1=m m2=0 if (m.ne.4) then m3=m+1 else m3=1 endif cas = castab(sh(m1),sh(m2),sh(m3)) if (cas.ne.0) then goto (31,32,33,34,35,36,37,38,39),cas 31 x1=xh(m1) y1=yh(m1) x2=xh(m2) y2=yh(m2) goto 40 32 x1=xh(m2) y1=yh(m2) x2=xh(m3) y2=yh(m3) goto 40 33 x1=xh(m3) y1=yh(m3) x2=xh(m1) y2=yh(m1) goto 40 34 x1=xh(m1) y1=yh(m1) x2=xsect(m2,m3) y2=ysect(m2,m3) goto 40 35 x1=xh(m2) y1=yh(m2) x2=xsect(m3,m1) y2=ysect(m3,m1) goto 40 36 x1=xh(m3) y1=yh(m3) x2=xsect(m1,m2) y2=ysect(m1,m2) goto 40 37 x1=xsect(m1,m2) y1=ysect(m1,m2) x2=xsect(m2,m3) y2=ysect(m2,m3) goto 40 38 x1=xsect(m2,m3) y1=ysect(m2,m3) x2=xsect(m3,m1) y2=ysect(m3,m1) goto 40 39 x1=xsect(m3,m1) y1=ysect(m3,m1) x2=xsect(m1,m2) y2=ysect(m1,m2) goto 40 40 if(SOLID((x1+x2)/2,(y1+y2)/2))cycle call vecout(x1,y1,x2,y2,k) endif 60 continue endif 80 continue endif 90 continue 100 continue end subroutine vecout(x1,y1,x2,y2,nz) use GrafLib implicit real*8(a-h,o-z) select case(nz) case(1);icol=1; case(2);icol=3; case(3);icol=2; case(4);icol=6; case(5);icol=4 end select call PLOT2((/x1,x2/),(/y1,y2/),icol,50,2d-3) end subroutine Vectors1(Nx,Ny,x,y,Vx,Vy,c,icol,ivec,dr,ivar) use Graflib implicit real*8(a-h,o-z) parameter (angle=0.3,tip=0.40) dimension x(Nx),y(Ny),Vx(Nx,Ny),Vy(Nx,Ny) logical SOLID Vmax = sqrt(maxval(Vx**2+Vy**2)); np=50 do i=2,Nx-1,ivec do j=2,Ny-1,ivec if(SOLID(x(i),y(j))) then cycle else if(ivar==1)then Vmod=sqrt(Vx(i,j)**2+Vy(i,j)**2) dx = c*Vx(i,j)/Vmod dy = c*Vy(i,j)/Vmod else dx = c*Vx(i,j)/Vmax dy = c*Vy(i,j)/Vmax end if x2=x(i)+dx; y2=y(j)+dy call Plot2((/x(i),x2/),(/y(j),y2/),icol,np,dr) cs=cos(angle); sn=sin(angle) dxi=-dx; dyi=-dy x3=x2+( dxi*cs+dyi*sn)*tip y3=y2+(-dxi*sn+dyi*cs)*tip x4=x2+( dxi*cs-dyi*sn)*tip y4=y2+( dxi*sn+dyi*cs)*tip call Plot2((/x2,x3/),(/y2,y3/),icol,np,dr) call Plot2((/x2,x4/),(/y2,y4/),icol,np,dr) end if end do end do end subroutine PLINES(Nx,Ny,x,y,Vx,Vy,Npl,xpl,ypl,dt,Nt) use Graflib implicit real*8(a-h,o-z) dimension x(Nx),y(Ny),Vx(Nx,Ny),Vy(Nx,Ny),xpl(Npl),ypl(Npl) do j=1,Npl xpold=xpl(j);ypold=ypl(j) do i=2,Nt call bilint(Nx,Ny,x,y,Vx,xpold,ypold,up) call bilint(Nx,Ny,x,y,Vy,xpold,ypold,vp) xp1=xpold+dt*up yp1=ypold+dt*vp call bilint(Nx,Ny,x,y,Vx,xp1,yp1,up1) call bilint(Nx,Ny,x,y,Vy,xp1,yp1,vp1) xp=xpold+0.5*dt*(up+up1) yp=ypold+0.5*dt*(vp+vp1) call Plot((/xpold,xp/),(/ypold,yp/),1,0,0) xpold=xp ypold=yp end do end do end subroutine bilint(N1,N2,x,y,f,xint,yint,Fint) implicit real*8(a-h,o-z) dimension x(N1),y(N2),f(N1,N2) do i=1,N1-1 do j=1,N2-1 if((x(i)<=xint).and.(xint<=x(i+1)).and. & (y(j)<=yint).and.(yint<=y(j+1)))then S=f(i,j)*(x(i+1)-xint)*(y(j+1)-yint) & +f(i+1,j)*(xint-x(i))*(y(j+1)-yint) & +f(i,j+1)*(x(i+1)-xint)*(yint-y(j)) & +f(i+1,j+1)*(xint-x(i))*(yint-y(j)) Fint=S/(x(i+1)-x(i))/(y(j+1)-y(j)) end if end do end do end 5.Результат:    Исходя из полученной визуализации несжимаемого вязкого течения в каверне, можно заметить, что в данном случае присутствуют два вихря. Первый вихрь порождает второй. В центре верхнего вихря скорость стремится к нулю, вблизи верхней стенки она максимальная, а вдали от нее минимальна, это объясняется тем, что в других местах энергия тратится на закрутки потока. Flow statistics: xmin= 0.000000000000000E+000 xmax= 1.00000000000000 ymin= 0.000000000000000E+000 ymax= 1.33300000000000 umin= -0.365000000000000 umax= 1.00000000000000 vmin= -0.625900000000000 vmax= 0.338000000000000 tao= 0.000000000000000E+000 1.301600104250015E-009 1.229600098483266E-009 -1.630400130584838E-009 -7.763200621783743E-009 -1.723200138017537E-008 -2.990400239512327E-008 -4.555200364843015E-008 -6.388800511702902E-008 -8.464000677913435E-008 -1.073600085988642E-007 -1.316800105467440E-007 -1.572800125971438E-007 -1.837600147180261E-007 -2.106400168709459E-007 -2.376000190302732E-007 -2.642400211639705E-007 -2.904000232592228E-007 -3.158400252968076E-007 -3.404000272639099E-007 -3.640000291541223E-007 -3.868000309802596E-007 -4.089600327551369E-007 -4.306400344915692E-007 -4.522400362215941E-007 -4.740800379708414E-007 -4.964000397585337E-007 -5.194400416038936E-007 -5.432800435133284E-007 -5.675200454548007E-007 -5.916800473898656E-007 -6.145600492224103E-007 -6.347200508371002E-007 -6.499200520545250E-007 -6.576000526696450E-007 -6.544800524197526E-007 -6.366400509908802E-007 -5.996800480306155E-007 -5.382400431096559E-007 -4.463200357474391E-007 -3.174400254249576E-007 -1.444000115655364E-007 8.016000642031442E-008 3.634400291092698E-007 7.120800570331520E-007 1.131200090602041E-006 1.624800130136313E-006 2.195200175821783E-006 2.840800227530304E-006 3.558400285005574E-006 4.344000347927217E-006 5.189600415654485E-006 6.085600487418480E-006 7.024000562578447E-006 7.994400640301415E-006 8.992000720202933E-006 1.000000080093743E-005 1.101600088231267E-005 1.204000096432866E-005 1.305600104570390E-005 1.408800112836065E-005 1.511200121037664E-005 1.616000129431488E-005 1.721600137889387E-005 1.831200146667661E-005 1.946400155894460E-005 2.068800165697935E-005 2.202400176398459E-005 2.350400188252332E-005 2.520000201836231E-005 2.717600217662754E-005 2.950400236308578E-005 3.228000258542602E-005 3.554400284685198E-005 3.919200313903395E-005 4.286400343313818E-005 4.571200366124515E-005 4.614400369584565E-005 4.170400334022944E-005 2.863200229324403E-005 0.000000000000000E+000 cf= 0.000000000000000E+000 2.603199961209297E-006 2.459199963355066E-006 -3.260799951410295E-006 -1.552639976863862E-005 -3.446399948644639E-005 -5.980799910879136E-005 -9.110399864244463E-005 -1.277759980959893E-004 -1.692799974775315E-004 -2.147199968004227E-004 -2.633599960756302E-004 -3.145599953126908E-004 -3.675199945235254E-004 -4.212799937224390E-004 -4.751999929189684E-004 -5.284799921250345E-004 -5.807999913454057E-004 -6.316799905872348E-004 -6.807999898552897E-004 -7.279999891519549E-004 -7.735999884724619E-004 -8.179199878120424E-004 -8.612799871659282E-004 -9.044799865221981E-004 -9.481599858713153E-004 -9.927999852061273E-004 -1.038879984519482E-003 -1.086559983808995E-003 -1.135039983086586E-003 -1.183359982366562E-003 -1.229119981684685E-003 -1.269439981083870E-003 -1.299839980630875E-003 -1.315199980401993E-003 -1.308959980494976E-003 -1.273279981026650E-003 -1.199359982128144E-003 -1.076479983959198E-003 -8.926399866986276E-004 -6.348799905395510E-004 -2.887999956965447E-004 1.603199976110459E-004 7.268799891686442E-004 1.424159978778363E-003 2.262399966287613E-003 3.249599951577188E-003 4.390399934577943E-003 5.681599915337564E-003 7.116799893951419E-003 8.687999870538714E-003 1.037919984533787E-002 1.217119981863499E-002 1.404799979066849E-002 1.598879976174832E-002 1.798399973201752E-002 1.999999970197678E-002 2.203199967169762E-002 2.407999964118005E-002 2.611199961090089E-002 2.817599958014489E-002 3.022399954962732E-002 3.231999951839448E-002 3.443199948692323E-002 3.662399945425988E-002 3.892799941992760E-002 4.137599938344957E-002 4.404799934363367E-002 4.700799929952623E-002 5.039999924898149E-002 5.435199919009210E-002 5.900799912071230E-002 6.455999903798107E-002 7.108799894070626E-002 7.838399883198739E-002 8.572799872255329E-002 9.142399863767627E-002 9.228799862480166E-002 8.340799875712399E-002 5.726399914669993E-002 0.000000000000000E+000 pw= 0.000000000000000E+000 7.477600598908970E-010 -1.173600093998016E-010 -1.474400118090214E-009 -2.930400234706703E-009 -4.342400347799068E-009 -5.656000453010207E-009 -6.850400548674175E-009 -7.912000633701691E-009 -8.832000707387935E-009 -9.592000768259178E-009 -1.019200081631542E-008 -1.062400085091592E-008 -1.088800087206067E-008 -1.099200088039042E-008 -1.096000087782742E-008 -1.079200086437167E-008 -1.053600084386767E-008 -1.021600081823767E-008 -9.872000790685426E-009 -9.560000765696179E-009 -9.312000745832929E-009 -9.192000736221681E-009 -9.224000738784680E-009 -9.440000756084929E-009 -9.856000789403928E-009 -1.044800083681942E-008 -1.116800089448692E-008 -1.194400095663966E-008 -1.265600101366640E-008 -1.316000105403365E-008 -1.326400106236340E-008 -1.279200102455916E-008 -1.153600092396141E-008 -9.304000745192179E-009 -5.872800470374530E-009 -1.014400081247092E-009 5.534400443270809E-009 1.406400112643839E-008 2.488800199337307E-008 3.830400306791071E-008 5.455200436927385E-008 7.378400590963669E-008 9.600000768899927E-008 1.211200097009541E-007 1.488000119179489E-007 1.784000142887237E-007 2.093600167684259E-007 2.408000192865732E-007 2.719200217790905E-007 3.017600241690878E-007 3.295200263924901E-007 3.546400284044449E-007 3.764800301536921E-007 3.948800316274171E-007 4.097600328192119E-007 4.213600337482994E-007 4.300800344467168E-007 4.366400349721318E-007 4.418400353886193E-007 4.466400357730692E-007 4.523200362280017E-007 4.603200368687515E-007 4.724000378362839E-007 4.910400393292313E-007 5.195200416103011E-007 5.626400450639433E-007 6.286400503501303E-007 7.308800585389146E-007 8.920000714436183E-007 1.150400092139841E-006 1.560800125010313E-006 2.196800175949934E-006 3.122400250084702E-006 4.321600346133118E-006 5.556000445000833E-006 6.159200493313380E-006 4.731200378939514E-006 -1.656800132699313E-006 -2.057600164800884E-005 0.000000000000000E+000 cp= 0.000000000000000E+000 1.495519977715016E-006 -2.347199965023995E-007 -2.948799956059457E-006 -5.860799912667276E-006 -8.684799870586400E-006 -1.131199983143807E-005 -1.370079979584218E-005 -1.582399976420403E-005 -1.766399973678590E-005 -1.918399971413613E-005 -2.038399969625474E-005 -2.124799968338013E-005 -2.177599967551232E-005 -2.198399967241288E-005 -2.191999967336656E-005 -2.158399967837335E-005 -2.107199968600274E-005 -2.043199969553948E-005 -1.974399970579148E-005 -1.911999971508981E-005 -1.862399972248078E-005 -1.838399972605706E-005 -1.844799972510338E-005 -1.887999971866608E-005 -1.971199970626832E-005 -2.089599968862534E-005 -2.233599966716767E-005 -2.388799964404107E-005 -2.531199962282182E-005 -2.631999960780144E-005 -2.652799960470201E-005 -2.558399961876871E-005 -2.307199965620042E-005 -1.860799972271920E-005 -1.174559982497692E-005 -2.028799969768525E-006 1.106879983506203E-005 2.812799958086015E-005 4.977599925827982E-005 7.660799885845186E-005 1.091039983742238E-004 1.475679978010655E-004 1.919999971389771E-004 2.422399963903428E-004 2.975999955654146E-004 3.567999946832659E-004 4.187199937605859E-004 4.815999928236010E-004 5.438399918961527E-004 6.035199910068515E-004 6.590399901795390E-004 7.092799894309048E-004 7.529599887800218E-004 7.897599882316594E-004 8.195199877882006E-004 8.427199874424938E-004 8.601599871826175E-004 8.732799869871144E-004 8.836799868321423E-004 8.932799866890911E-004 9.046399865198140E-004 9.206399862813952E-004 9.447999859213832E-004 9.820799853658680E-004 1.039039984517098E-003 1.125279983232022E-003 1.257279981265069E-003 1.461759978218079E-003 1.783999973416329E-003 2.300799965715409E-003 3.121599953484536E-003 4.393599934530260E-003 6.244799906945231E-003 8.643199871206287E-003 1.111199983441830E-002 1.231839981644154E-002 9.462399858999253E-003 -3.313599950623513E-003 -4.115199938678742E-002 0.000000000000000E+000 Xtr= 1.077402832478325E-005 Xd= 2.886547061016403E-007 CXtr= 1.616104047032179E-002 CXd= 4.329820051175055E-004 6.Графики: 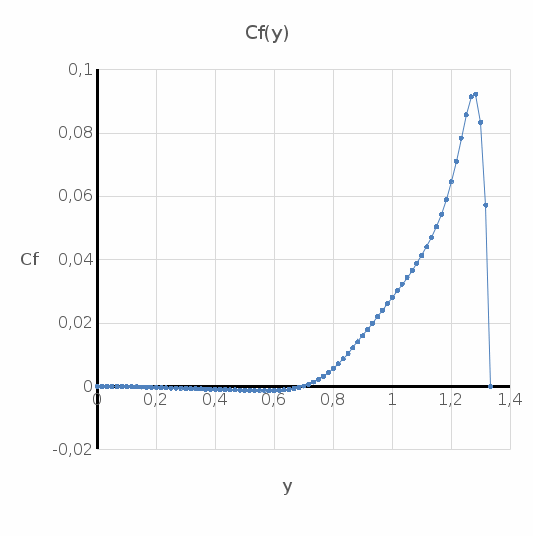 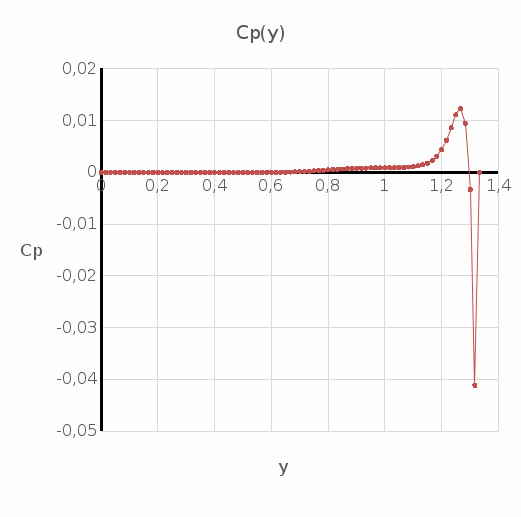 7.Вывод: В ходе лабораторной работы по табличным данным было визуализировано поле векторов скоростей, линии тока и изолинии модуля скорости 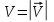 и компонент скорости 𝑢 и v, были определены действующие на правую стенку силы и их коэффициенты. Также были построены графики зависимости коэффициента трения и давления от координаты заданной стенки, по которым видно, что полученные знаки производных соответствуют изменению направления векторов скоростей. и компонент скорости 𝑢 и v, были определены действующие на правую стенку силы и их коэффициенты. Также были построены графики зависимости коэффициента трения и давления от координаты заданной стенки, по которым видно, что полученные знаки производных соответствуют изменению направления векторов скоростей. |
