Лабораторная работа № 1 по курсу общей физики. Изучение прямолинейного движения тел на машине Атвуда. ТУСУР, Крафт Н.А. лр1. Лабораторная работа по курсу "Общая физика"
 Скачать 106.01 Kb. Скачать 106.01 Kb.
|
|
Лабораторная работа по курсу "Общая физика" Изучение прямолинейного движения тел на машине Атвуда 1. ЦЕЛЬ РАБОТЫ Целью работы является изучение закона прямолинейного ускоренного движения тел под действием сил земного тяготения с помощью машины Атвуда. прямолинейный движение атвуд погрешность 2. ОПИСАНИЕ УСТАНОВКИ И МЕТОДИКИ ЭКСПЕРИМЕНТА 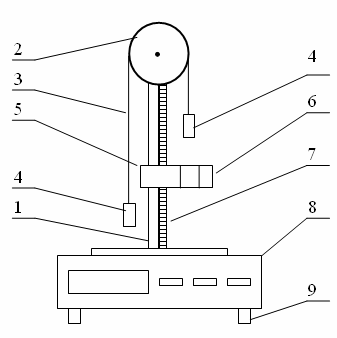 Рис. 1. Машина Атвуда: 1 -стойка; 2 – блок; 3 – нить; 4 – грузы; 5 – средний кронштейн; 6 – фотодатчик; 7 – линейка; 8 – миллисекундомер; 9 – опора Схема экспериментальной установки на основе машины Атвуда приведена на рис. 1. На вертикальной стойке 1 крепится легкий блок 2, через который перекинута нить 3 с грузами 4 одинаковой массы. В верхней части стойки расположен электромагнит, который может удерживать блок, не давая ему вращаться. На среднем кронштейне 5 закреплен фотодатчик 6. На корпусе среднего кронштейна имеется риска, совпадающая с оптической осью фотодатчика. Средний кронштейн имеет возможность свободного перемещения и фиксации на вертикальной стойке. На вертикальной стойке укреплена миллиметровая линейка 7, по которой определяют начальное и конечное положения грузов. Начальное положение определяют по нижнему срезу груза, а конечное – по риске на корпусе среднего кронштейна. Миллисекундомер 8 представляет собой прибор с цифровой индикацией времени. Регулировочные опоры 9 используют для регулировки положения экспериментальной установки на лабораторном столе. Принцип работы машины Атвуда заключается в том, что когда на концах нити висят грузы одинаковой массы, то система находится в положении безразличного равновесия. Если на правый груз положить перегрузок, то система грузов выйдет из состояния равновесия и начнет двигаться. 3. ОСНОВНЫЕ РАСЧЕТНЫЕ ФОРМУЛЫ Стандартная абсолютная погрешность измерения времени опускания груза с пригрузком: 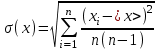 , (1) , (1)где xi – время опускания груза с пригрузком при i-том измерении (i=1,...,n); n – число измерений (n = 5); <x> – среднее значения времени опускания груза с пригрузком. Случайная погрешность: 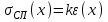 , (2) , (2)где k – коэффициент Стьюдента, ε(x) – результат среднеквадратичного отклонения. Общая погрешность: 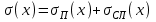 , (3) , (3)где: 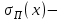 приборная погрешность. приборная погрешность.Угловой коэффициент экспериментальной прямой: = 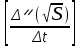 . (4) . (4)Величина ускорения, определяемого из линеаризованного графика: a = 22. (5) Среднее значение измеренной величины: 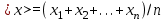 . (6) . (6)где: 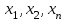 – результаты измерения величины, n- число измерений. – результаты измерения величины, n- число измерений.4. РЕЗУЛЬТАТЫ РАБОТЫ И ИХ АНАЛИЗ. Измеренные значения и результаты их обработки приведены в табл. 1. Рисунки 2, 3, 4 отражают зависимости пути от времени. В табл. 2 представлены результаты расчетов доверительных интервалов. Таблица 1. Результат прямых и косвенных измерений
Для расчета значений ‹t› и ‹t²› необходимо из полученных результатов измерения времени рассчитать среднеарифметическое значение. Воспользуемся формулой (6), подставив вместо х параметр t и t2. Произведем расчет среднеквадратичного отклонения, воспользовавшись выражением (1). для S1 = 40 см: ε(t)=0,065229 с; ε(t  )=0,578735 с )=0,578735 с ; ;для S2 = 33.9 см: ε(t)=0,056955 с; ε(t  )=0,463157 с )=0,463157 с ; ;для S3 = 31 см: ε(t)=0.072834 с; ε(t  )=0.570447 с )=0.570447 с ; ;для S4 = 28 см: ε(t)=0.058908 с; ε(t  )=0.412886 с )=0.412886 с ; ;для S5 = 24 см: ε(t)=0.055323 с; ε(t  )=0.530857 с )=0.530857 с . .Зная среднеквадратичное отклонение, мы можем произвести расчет случайной погрешности для t и t  ,для этого воспользуемся выражением (2), где k – коэффициент Стьюдента, а вместо х подставляются значения t и t ,для этого воспользуемся выражением (2), где k – коэффициент Стьюдента, а вместо х подставляются значения t и t . При доверительной вероятности α=0,95 и числе измерений n=5 коэффициент Стьюдента k=2,8. Получим: . При доверительной вероятности α=0,95 и числе измерений n=5 коэффициент Стьюдента k=2,8. Получим:для S1 = 40 см: σ 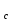 (t)=2,8*0,065229 с=0,18 с; (t)=2,8*0,065229 с=0,18 с;σ 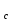 (t (t )=2,8*0,578735 с )=2,8*0,578735 с =1,62 с =1,62 с ; ;для S2 = 33.9 см: σ 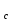 (t)=2,8*0,056955 с=0,15 с; (t)=2,8*0,056955 с=0,15 с;σ 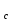 (t (t )=2,8*0,463157 с )=2,8*0,463157 с =1,30 с =1,30 с ; ;для S3 = 31 см: σ 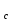 (t)=2,8*0,072834 с=0,2 с; (t)=2,8*0,072834 с=0,2 с;σ 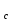 (t (t )=2,8*0,570447 с )=2,8*0,570447 с =1,60 с =1,60 с ; ;для S4 = 28 см: σ 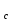 (t)=2,8*0,058908 с=0,16 с; (t)=2,8*0,058908 с=0,16 с;σ 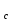 (t (t )=2,8*0,412886 с )=2,8*0,412886 с =1,15 с =1,15 с ; ;для S5 = 24 см: σ 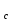 (t)=2,8*0,055323 с=0,15 с; (t)=2,8*0,055323 с=0,15 с;σ 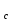 (t (t )=2,8*0,530857 с )=2,8*0,530857 с =1,48 с =1,48 с . .Приборная погрешность миллисекундомера σn(t) установленного на машине Атвуда изначально нам не указана. Нам известно, что если прибор цифровой, то σn(t) равна 1 в младшем разряде прибора. Делаем вывод, приборная погрешность миллисекундомера составляет 0,001с. Выяснив приборную и случайные погрешности, мы можем вычислить общую погрешность по формуле (3). Получаем: для S1 = 40 см: σ(t)=0,001с+0,182641с=0,18 с; σ(t  )=0,001+1,620458с )=0,001+1,620458с =1,62 с =1,62 с ; ;для S2 = 33.9 см: σ(t)=0,001+0,159474=0,16 с; σ(t  )=0,001+1,296839с )=0,001+1,296839с =1,30 с =1,30 с ; ;для S3 = 31 см: σ(t)=0,001+0,203935с=0,20 с; σ(t  )=0,001+1,597251с )=0,001+1,597251с =1,59 с =1,59 с ; ;для S4 = 28 см: σ(t)=0,001+0,164942с=0,16 с; σ(t  )=0,001+1,156080с )=0,001+1,156080с =1,15с =1,15с ; ;для S5 = 24 см: σ(t)=0,001+0,154904с=0,15 с; σ(t  )=0,001+1,486399с )=0,001+1,486399с =1,48с =1,48с . .Доверительный интервал равен 2σ(х), где вместо параметра х подставим t и t2. Получается, что для расчета интервала необходимо общую погрешность каждого параметра для каждой точки умножить на 2. Полученные результаты представлены в табл. 2. Таблица 2. Таблица доверительных интервалов
Исходя из полученных данных, построим три графика зависимости. 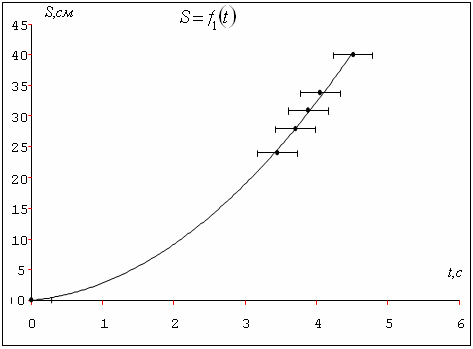 Рис. 2. Зависимость пройденного пути от времени 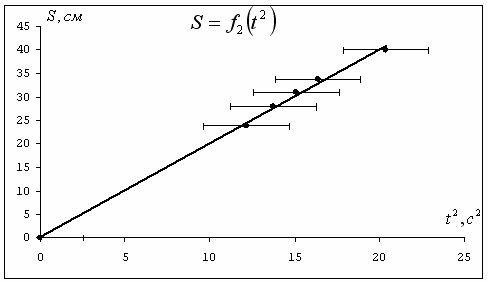 Рис. 3. Зависимость пути от квадрата времени 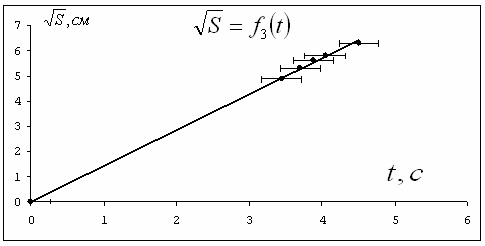 Рис. 4. Зависимость корня квадратного из пути от времени Исходя из формул (4) и (5), вычислим величину ускорения. Взяв интервал по a = 22 =2 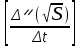  =2 =2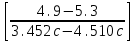  ≈ 4.251м/с ≈ 4.251м/с . .5. Контрольные вопросы 1. Какие силы действуют на груз с перегрузом во время движения? Ответ: На груз с перегрузом во время движения действует сила тяжести и сила натяжения нити. 2. Запишите уравнение движения для каждого из грузов. Ответ: Уравнение движения грузов имеют вид: (M + m)g – T1 = (M + m)a1; Mg – T2 = Ma2. В силу нерастяжимости нити a2 = – a1; при невесомом блоке T2 = T1. (M + m)g – T1 = (M + m)a1; Mg – T1 = – Ma1. 3. Укажите возможные причины, обусловливающие несовпадение теоретических выводов с результатами измерений. Ответ: Погрешности измерений физических величин обуславливает несовпадение теоретических выводов с результатами измерений. 4. Каким образом из линеаризованного графика можно оценить систематическую погрешность измерения времени? Ответ: Систематическая погрешность приводит к тому, что прямая не будет проходить через начало координат. Величина отклонения прямой от начала координат будет соответствовать систематической погрешности. 5. Укажите физические допущения, используемые при теоретическом анализе движения грузов в машине Атвуда. Ответ: Физические допущения, используемые при теоретическом анализе движения грузов в машине Атвуда: блок и нить невесомы, нить нерастяжима, сила трения мала. Вывод На примере выполненной нами лабораторной работы мы еще раз убедились в справедливости закона прямолинейного ускорения под действием сил земного тяготения, с помощью машины Атвуда: Нам удалось в пределах погрешностей измерений построить линеаризованный график 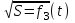 , который и свидетельствует справедливость вышеописанного закона. , который и свидетельствует справедливость вышеописанного закона. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

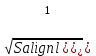 = 6.3 см0,5
= 6.3 см0,5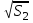 =5.8 см0,5
=5.8 см0,5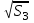 =5.6 см0,5
=5.6 см0,5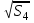 =5.3 см0,5
=5.3 см0,5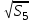 =4.9 см0,5
=4.9 см0,5