Ономерная минимизация функций. ЛАБОРАТОРНАЯ РАБОТА-одномерная минимизация функций. Лабораторная работа по теории оптимизации информационных систем 1 одномерная минимизация функций
 Скачать 120.36 Kb. Скачать 120.36 Kb.
|
|
Министерство науки и высшего образования Российской Федерации Ульяновский государственный технический университет Лабораторная работа по теории оптимизации информационных систем № 1_ ОДНОМЕРНАЯ МИНИМИЗАЦИЯ ФУНКЦИЙ (Название лабораторной работы) Учебная группа ИСТМД-11
Ульяновск, 2021 ЦЕЛЬ РАБОТЫ: изучение прямых методов минимизации функций. Задачи: изучить следующие методы минимизации: - перебора; - поразрядного поиска; - дихотомии; - золотого сечения; - метод парабол. Программа лабораторной работы Ознакомиться с вышеуказанными методами. Составить программу в среде MATLAB. Получить результаты и сделать выводы. ОБОРУДОВАНИЕ И ПРИНАДЛЕЖНОСТИ: Среда программирования MATLAB. КРАТКАЯ ТЕОРИЯ: Оптимизация – задача нахождения экстремума (минимума или максимума) целевой функции в некоторой области конечномерного векторного пространства, ограниченной набором линейных и/или нелинейных равенств и/или неравенств. Методы, использующие только значения функции и не требующие вычисления ее производных, называются прямыми методами минимизации. Большим достоинством прямых методов является то, что от целевой функции не требуется дифференцируемости. Более того, она может быть не задана в аналитическом виде. Единственное, на чем основаны алгоритмы прямых методов минимизации, это возможность определения значений f(х) в заданных точках. Метод перебора является простейшим из прямых методов и состоит в следующем. Разобьем отрезок [a,b], на n равных частей точками деления Xi = a + i(b-a)/n, i=0,...,n. Вычислив значения f(x) в точках Xi , путем сравнения найдем точку Xm, 0 ≤ m ≤ n, для которой f(X) = min f(Xi), 0 ≤ i ≤ n Далее, положим X* ≈ Xm, f* ≈ f(Xm) Необходимо отметить, что погрешность определения точки минимума X* функции f(X) методом перебора не превосходит величины En = (b-a)/2. Метод поразрядного поиска представляет собой усовершенствованный метод перебора с целью уменьшения количества значений, которые необходимо находить в процессе минимизации. Во-первых, если f(Xi) ≤ f(Xi+1) , то отпадает необходимость вычислять f(X) в точках Xi+2, Xi+3 и т.д., так как из унимодальности функции следует, что X* ≤ Xi+1. Во-вторых, разумно было бы сначала определить отрезок, содержащий точку X* с небольшой точностью, а затем искать ее на этом отрезке с меньшим шагом lискретизации, повышая точность. Такая возможность улучшения метода перебора реализована в методе поразрядного поиска, в котором перебор точек отрезка происходит сначала с шагом Δ= Xi+1 -Xi > ε до тех пор, пока не выполнится условие f(Xi) ≤ f(Xi+1) или пока очередная из этих точек не совпадет с концом отрезка. После этого шаг уменьшается (обычно в четыре раза), и перебор точек с новым шагом производится в противоположном направлении до тех пор, пока значения f(X) не перестанут уменьшаться или очередная точка не совпадет с концом отрезка и т.д. Процесс завершается, когда перебор в данном направлении закончен, а использованный при этом шаг дискретизации не превосходит ε. Метод дихотомии В этом методе пробные точки Х1 и Х2 располагаются близко к середине очередного отрезка [a,b] , т.е. X1 = (b + a - δ)/2, X2 = (b + a + δ)/2 где δ − малое число. При этом отношение длин нового и исходного отрезков τ = (b-X1)/(b-a) = (X2 - a)/(b-a) близко к 1/2, этим и объясняется название метода. Отметим, что для любых точек X1 b X2 и величина τ > 1/2, поэтому указанный выбор пробных точек объясняется стремлением обеспечить максимально возможное относительное уменьшение отрезка на каждой итерации поиска X*. В конце вычислений методом дихотомии в качестве приближенного значения X* берут середину последнего из найденных отрезков [a,b], убедившись предварительно, что достигнуто неравенство: (b-a)/2 ≤ ε Метод золотого сечения. Рассмотрим такое симметричное расположение точек и на отрезке, при котором одна из них становится пробной точкой на новом отрезке, полученном после исключения части исходного отрезка. Использование таких точек позволяет на каждой итерации метода золотого сечения, кроме первой, ограничиться определением только одного значения f(X), так как другое значение уже найдено на одной из предыдущих итераций. Найдем точки X1 и X2, обладающие указанным свойством. Рассмотрим сначала отрезок [0,1] и для определенности предположим, что при его уменьшении исключается правая часть этого отрезка. Пусть X2 = τ , тогда симметрично расположенная точка X1 = 1−τ. 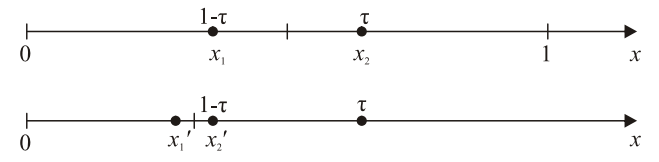 Пробная точка x1 отрезка [0,1] перейдет в пробную точку X2′ = 1 - τ нового отрезка [0,τ]. Чтобы точки X2 = τ и X2′ = 1−τ делили отрезки [0,1] и [0,τ] в одном и том же отношении, должно выполняться равенство 1/τ = τ/(1-τ) или τ^2 = 1-τ, откуда находим положительное значение 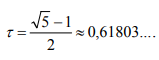 Таким образом, 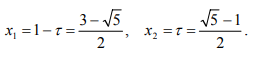 Для произвольного отрезка [a,b] выражения для пробных точек примут вид 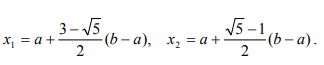 На каждой итерации отрезок поиска точки минимума уменьшается в одном и том же отношении 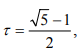 поэтому в результате итераций его длина становится Δn = τ^n(b-a). Таким образом, точность определения точки после итераций находится из равенства 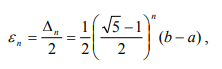 а условием окончания поиска точки X* с точностью ε служит неравенство εn ≤ ε . Метод парабол представляет собой простейший вариант полиномиальной аппроксимации, использующий полиномы второго порядка. На каждой итерации этого метода строится квадратный трехчлен, график которого (парабола) проходит через три выбранные точки графика функции f(X). 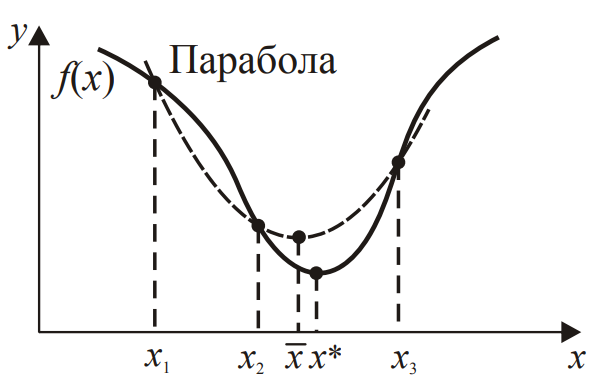 Рассмотрим унимодальную на отрезке [a,b] функцию f(x), достигающую минимума во внутренней точке этого отрезка. Выберем три точки x1, x2 и x3 отрезка, для которых выполняются неравенства Для определения таких точек, как правило, бывает достаточно нескольких проб. Можно также совершать итерации методом золотого сечения до тех пор, пока для пробных точек очередного отрезка и одного из его концов не станут выполняться неравенства. Из унимодальности функции f(x) следует, что x* ∈ [x1,x2] . Составим квадратный трехчлен график которого проходит через точки (x1,f(x1)), (x2,f(x2)), (x3, F(x3))графика функции f(x). Будем считать, что хотя бы одно из неравенств для f(x) является строгим. Тогда ветви искомой параболы будут направлены вверх, а точка минимума x трехчлена q(x) будет принадлежать отрезку [x1,x3]. Определяя коэффициенты a0, a1, a2 из системы уравнений 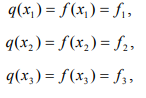 находим: 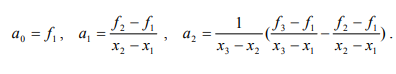 Точку минимума x вычислим, приравняв производную квадратного трехчлена к нулю. В результате получим 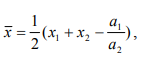 Заметим, что на каждой итерации метода парабол, кроме первой, определяется только одно новое значение f(x). Условием окончания поиска минимума является близость к нулю разности Δ чисел x, найденных на данной и предыдущей итерациях, т.е. неравенство Δ ≤ ε. ВЫПОЛНЕНИЕ РАБОТЫ Исследовать методы минимизации будем на примере функции: 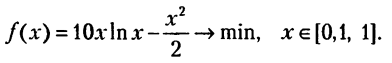 Текст программы: % Вариант № 7 % f(x)=10*x*log(x)-(x^2/2), при 0.1 < x < 1.0 % e=0.0001 % посмотрим график ezplot ('10*x*log(x)-(x^2/2)', [0.1 1.0]) hold on format long % 1. Метод перебора % по графику видно, что минимум функции находится между x=0.3 и x=0.5 f = @(x) 10*x*log(x)-(x^2/2) % наша функция h = 0.00001; % задаем шаг x = 0.3; % начальное приближение i = 0; % счетчик итераций while f(x+h) <= f(x) % пока условие выполняется, ф-я убывает x = x + h; i = i + 1; end disp('1. Метод перебора, x= :') disp(x) % решение - точка, когда ф-я стала возрастать (x=0.3822) disp('затрачено итераций, i= :') disp(i) % 0.3822 % 2. Метод поразрядного поиска e = 0.00001; % заданная погрешность h = 0.01; % задаем первоначальный шаг x = 0.3; % начальное приближение i = 0; % счетчик итераций while h > e while f(x+h) <= f(x) % пока условие выполняется, ф-я убывает x = x + h; i = i + 1; end %disp(x) h = h/10; % уменьшаем шаг и повторяем цикл end disp('2. Метод поразрядного поиска, x= :') disp(x) % решение, точка, когда ф-я стала возрастать, x=0.3822 disp('затрачено итераций, i= :') disp(i) % 12 % 3. Метод дихотомии e = 0.00001; % заданная погрешность a = 0.3; % задаем начальный отрезок [a,b] b = 0.5; i=0; % счетчик итераций while (b-a)/2 > e % пока не добьемся требуемой точности x1 = (a+b+e)/2; % вычисляем окрестности середины отрезка x2 = (a+b-e)/2; if f(x1) > f(x2) % вычисляем значения ф-и в этих точка и сравниваем b=x2; % задаем новый отрезок else a=x1; % задаем новый отрезок end i = i+1; end disp('3. Метод дихотомии, x= :') disp((x1+x2)/2) disp('затрачено итераций, i= :') disp(i) % 13 % 4. Метод золотого сечения e = 0.00001; % заданная погрешность a = 0.3; % задаем начальный отрезок [a,b] b = 0.5; i=0; % счетчик итераций r=(sqrt(5)+1)/2; % золотой коэффициент a=0.3; % начальные точки b=0.5; e=0.00001; a2= a; b2= b; while abs(b-a) >= e % пока погрешность больше требуемой x1= b-(b-a)/r; x2= a+(b-a)/r; y1= f(x1); y2= f(x2); if y1 >= y2 a=x1; else b=x2; end i=i+1; end disp('4. Метод золотого сечения, x= :') x=(a+b)/2; disp(x) disp('затрачено итераций, i= :') disp(i) % 5. Метод парабол e=0.00001; % заданная погрешность x0 = 0.3; % начальное приближение delta=0.01; dx=0.0001; h=0.5*dx; i=0; % счётчик итераций while delta>e f1=f(x0+dx); f2=f(x0); f3=f(x0-dx); x=x0-h*(f1-f3)/(f1-2*f2+f3); % получаем новый минимум delta=abs(x-x0); x0=x; i=i+1; end; disp('5. метод парабол, x= :') disp(x0) disp('затрачено итераций, i= :') disp(i) Результаты выполнения: 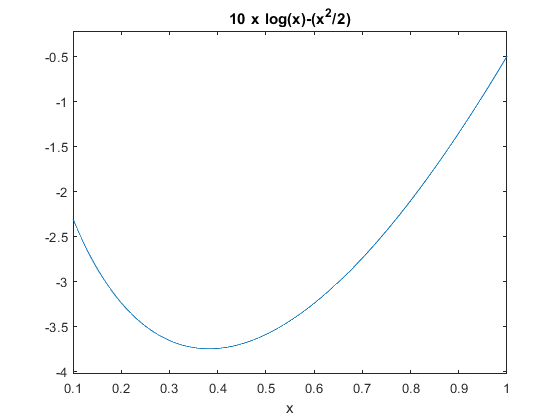 f = function_handle with value: @(x)10*x*log(x)-(x^2/2) 1. Метод перебора, x= : 0.382210000000082 затрачено итераций, i= : 8221 2. Метод поразрядного поиска, x= : 0.382200000000000 затрачено итераций, i= : 12 3. Метод дихотомии, x= : 0.382201258544922 затрачено итераций, i= : 13 4. Метод золотого сечения, x= : 0.382211430777835 затрачено итераций, i= : 21 5. метод парабол, x= : 0.382212422001853 затрачено итераций, i= : 4 Сведем результаты в таблицу:
ВЫВОД: Из таблицы видно, что наименее эффективным методом является метод перебора, остальные методы на два порядка производительней. Наилучший результат показал метод парабол. |
