ЛР_4-Показатели качества. Лабораторная работа. Показатели качества асу цель работы
 Скачать 265.29 Kb. Скачать 265.29 Kb.
|
|
Лабораторная работа. Показатели качества АСУ Цель работы: изучение математических методов оценки устойчивости линейных систем при помощи программы Scilab. Задания к работе: Ввести модель системы в виде передаточной функции. Получить переходный процесс. Определить коэффициент усиления в установившемся режиме. Определить установившееся значение выхода по результатам моделирования. Определить перерегулирование в процентах. Определить время переходного процесса (для коридора 5%). Проверить устойчивость разомкнутой системы с помощью критерия Гурвица. Найти полюса и нули передаточной функции разомкнутой системы и представить их графически, проверить устойчивость системы. Проверить устойчивость замкнутой системы с помощью критерия Михайлова (и следствия из него). Проверить устойчивость замкнутой системы с помощью критерия Найквиста. Проверить устойчивость замкнутой системы с помощью логарифмического критерия устойчивости. Варианты Индивидуальных заданий: 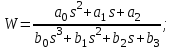
Контрольные вопросы: Понятие устойчивости для линейных САР. Условия устойчивости, типы границы устойчивости. Необходимое условие устойчивости САР, достаточное для систем 1-ого и 2-ого порядков. Критерий устойчивости Гурвица. Критерий устойчивости Михайлова. Свойства, примеры годографов Михайлова. Критерий устойчивости Найквиста. Свойства, примеры годографов Найквиста. Определение устойчивости по ЛАЧХ & ЛФЧХ. Методика построения асимптотических ЛАЧХ & ЛФЧХ линейных систем. Определение запаса устойчивости по амплитуде и по фазе. Пример выполнения 1. Ввести модель системы в виде передаточной функции 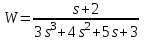  2. Получить переходный процесс. Построим график переходного процесса и зададим названия этого графика и осей, добавим координатную сетку.  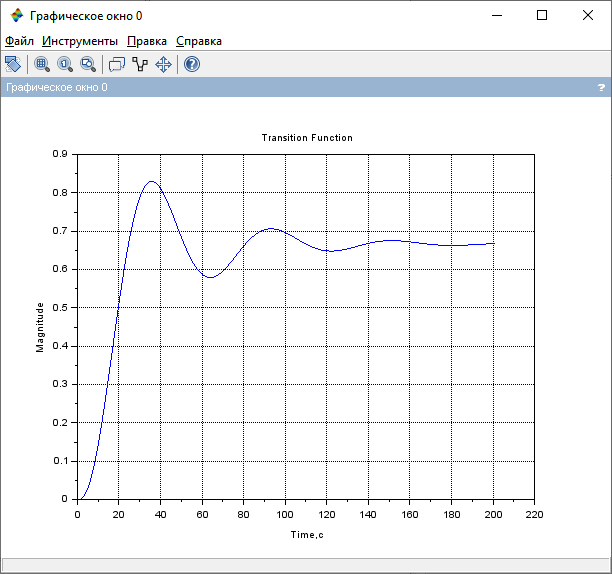 3. Определить коэффициент усиления в установившемся режиме.  4. Определить установившееся значение выхода по результатам моделирования.  Индекс $ означает последний элемент массива. 5. Определить перерегулирование в процентах.  Если для вашей системы получилось отрицательное значение yLast, для вычисления перерегулирования и времени переходного процесса нужно выполнить «зеркальное отражение»: использовать значения yStep и yLast с обратными знаками. 6. Определить время переходного процесса (для коридора 5%). 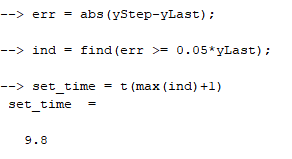 7. Проверить устойчивость разомкнутой системы с помощью критерия Гурвица. Характеристическое уравнение: 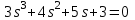 Составим определитель Гурвица: 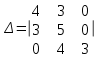 Проверка устойчивости: Δ1 = С1 = 4 > 0  Δ2 = 11 > 0  или Δ3 = С3Δ2 = 3 * 11 = 33 > 0 Следовательно, по критерию Гурвица разомкнутая система устойчива, потому что … 8. Найти полюса и нули передаточной функции разомкнутой системы и представить их графически, проверить устойчивость системы. Найдем нули и полюса передаточной функции разомкнутой системы. Корни характеристического уравнения разомкнутой системы: 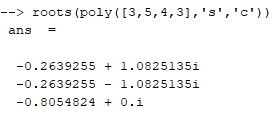 Изобразим корни характеристического уравнения графически. 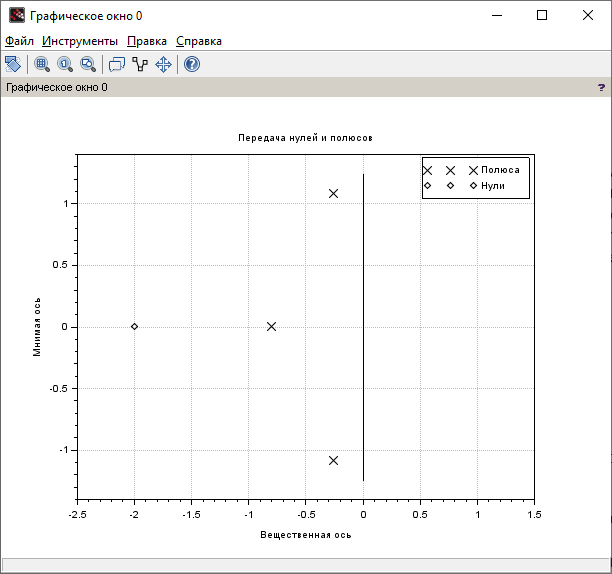 Система устойчива, потому что … 9. Проверить устойчивость замкнутой системы с помощью критерия Михайлова (и следствия из него). Характеристическое уравнение замкнутой системы:  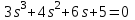 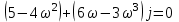 Построим годограф Михайлова  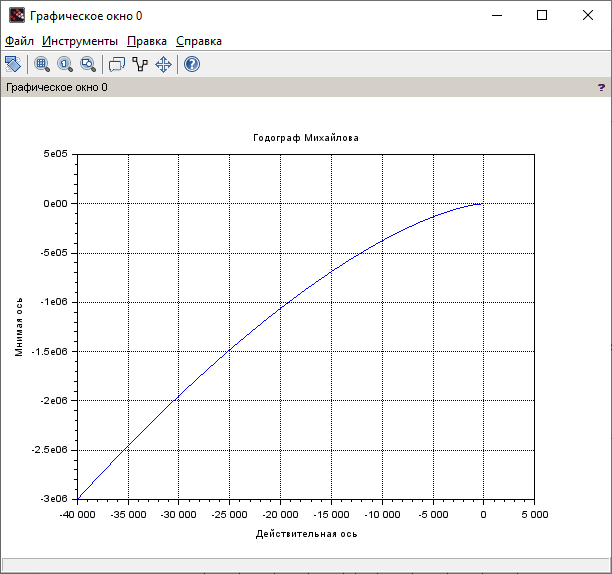 Закроем графическое окно и пересчитаем масштаб  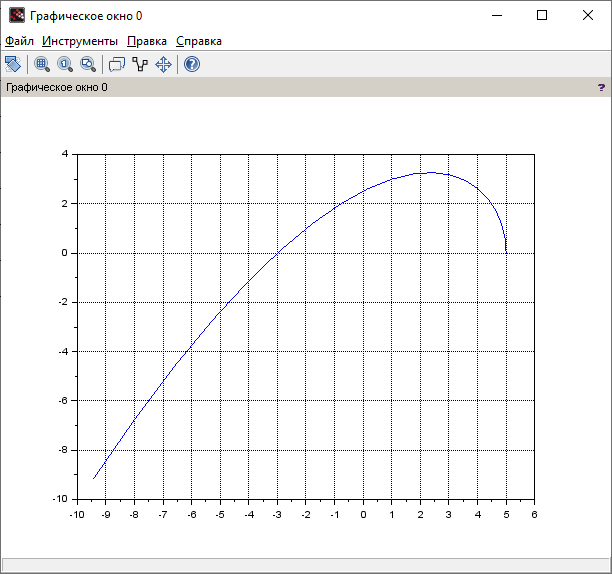 По критерию Михайлова замкнутая системы устойчива, потому что … Найдем корни полинома  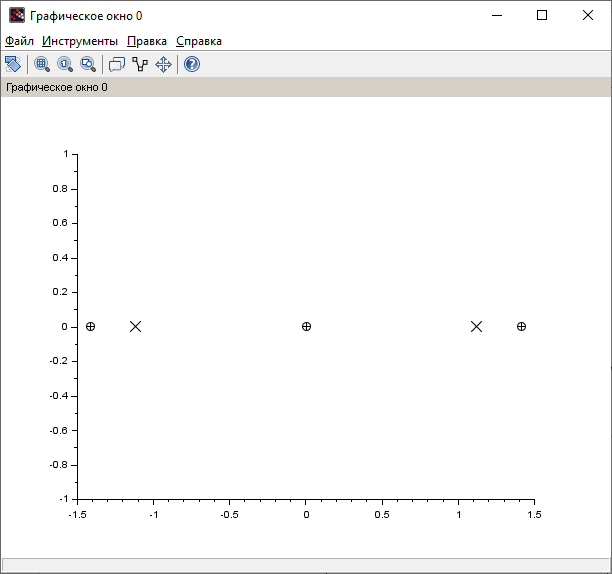 Согласно следствию из критерия Михайлова, замкнутая система устойчива, потому что… 10. Проверить устойчивость замкнутой системы с помощью критерия Найквиста. Построим годограф Найквиста 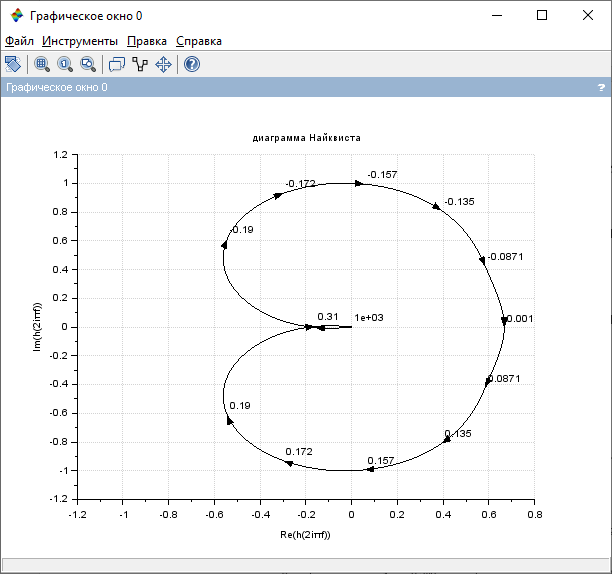 По критерию Найквиста система устойчива, потому что 11. Проверить устойчивость замкнутой системы с помощью логарифмического критерия устойчивости. Проверим устойчивость замкнутой системы с помощью логарифмического критерия устойчивости. И определим запасы устойчивости по фазе и амплитуде.  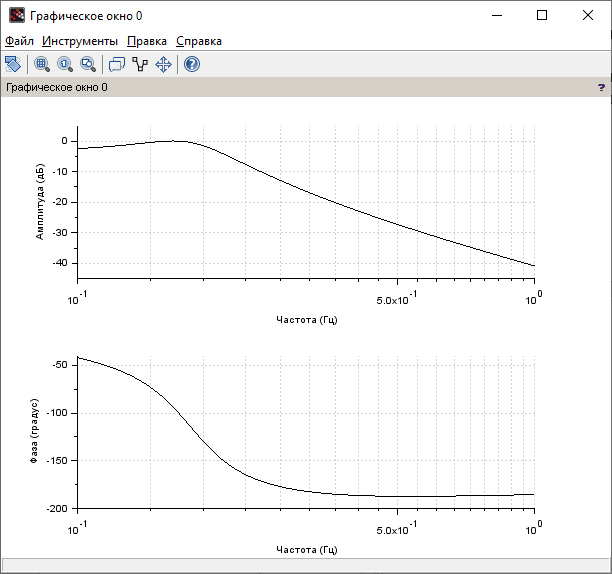  Где, fr – частота пересечения ЛАЧХ с осью -180°; gm – запас устойчивости по амплитуде; fr2 – частоты среза pm – запас устойчивости по фазе Система устойчива, потому что… |
