Лабораторная работа Решение дифференциальных уравнений в Matlab
 Скачать 0.51 Mb. Скачать 0.51 Mb.
|
|
РОССИЙСКИЙ УНИВЕРСИТЕТ ТРАНСПОРТА (МИИТ) Кафедра «Управление и защита информации» ЛАБОРАТОРНАЯ РАБОТА «Решение дифференциальных уравнений в Matlab» по дисциплине «ИСТОРИЯ И МЕТОДОЛОГИЯ НАУКИ И ТЕХНИКИ В ОБЛАСТИ УПРАВЛЕНИЯ» Выполнила: студентка группы ТУУ-151 Филонец Татьяна Проверила: доц. Зольникова Н.Н. Москва 2017 Задание №1 Решить дифференциальное уравнение: 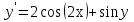 при начальном условии 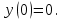 Решим данную задачу Коши с помощью метода Рунге-Кутта 4-5 порядка точности, используя функцию ode45(). Для этого запишем исходное уравнение как функцию в Matlab: function y = dy( x, y ) %Уравнение, задающее производную y = 2*cos(2*x) + sin(y); end Также необходимо задать начальные условия и интервал, на котором будет искаться решение. %Начальное условие y0 = 0; %Интервал, на которм будет находится решение interval = [0, 50]; %Решение с помощью метода Рунге-Кутта 4-5 порядка точности [X,Y] = ode45(@dy, interval, y0); plot(X, Y) %изображение графика функции grid on %создание сетки на графике  Задание №2 Решить задачу Коши и краевую задачу для дифференциального уравнения 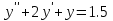 Начальные условия: 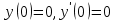 Граничные условия:  Аналитическое решение Для нахождения решения данного дифференциального уравнения следует найти общее решение соответствующего однородного дифференциального уравнения 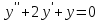 Составляем и решаем характеристическое уравнение: 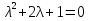 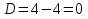 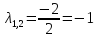 Характеристическое уравнение имеет два кратных действительных корня, следовательно, общее решение однородного уравнения имеет вид:  Найдем частное решение. Так как в исходном уравнении правая часть представляет собой константу, то частное решение будет иметь вид: 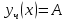 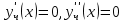 Подставляем частное решение в исходное уравнение. Получаем: 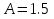 Таким образом, частное решение имеет вид: 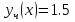 Общее решение исходного дифференциального уравнения записывается в виде: 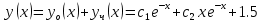 При этом производная 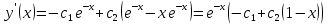 Решение задачи Коши. Для нахождения 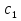 и и 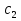 подставим начальные условия и решим систему: подставим начальные условия и решим систему:  Таким образом, при данных начальных условиях получаем решение в виде: 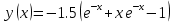 Решение краевой задачи. Для определения 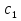 и и 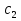 подставим краевые условия. подставим краевые условия.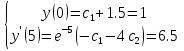 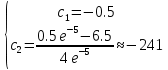 Таким образом, при данных краевых условиях получаем решение в виде:  Решение с помощью Matlab. Решим задачу Коши аналитически с помощью метода dsolve() и методом Рунге-Кутта с помощью функции ode45(). В функцию dsolve() необходимо записать исходное уравнение, начальные или граничные условия и переменную, по которой происходит дифференцирование. Символ «Dy» обозначает первую производную, «D2y» соответственно вторую производную. %Аналитическое решение Y = dsolve('D2y+2*Dy+y=1.5', 'y(0)=0', 'Dy(0)=0', 'x') y = ezplot(Y, [0,20]) %изображение графика символьного выражения set(y, 'LineWidth', 2); %установка толщины линии axis([0 20 0 2]); %задание границ графика grid on; %создание сетки на графике hold on; %следующий график будет рисоваться в этом же окне  Для использования функции ode45() запишем исходное уравнение в виде системы: function F = dy2( x, y ) %Представление исходного уравнения в виде системы % ОДУ первого порядка % y(1) -> y(x) % y(2) -> y'(x) F = [y(2) 1.5 - 2*y(2) - y(1)]; end В данном случае метод ode45() вернет значения y(x) и y’(x). %Решение с помощью метода Рунге-Кутта 4-5 порядка точности %Начальное условие y0 = [0, 0]; %Интервал, на которм будет находится решение interval = [0, 20]; [X,Y] = ode45(@dy2, interval, y0); %Значения искомой функции находятся в первом столбце матрицы Y plot(X, Y(:,1), ':r', 'LineWidth', 1.5) %изображение графика функции legend('Аналитическое решение','Метод Рунге-Кутта'); Оба графика решений полностью совпали. 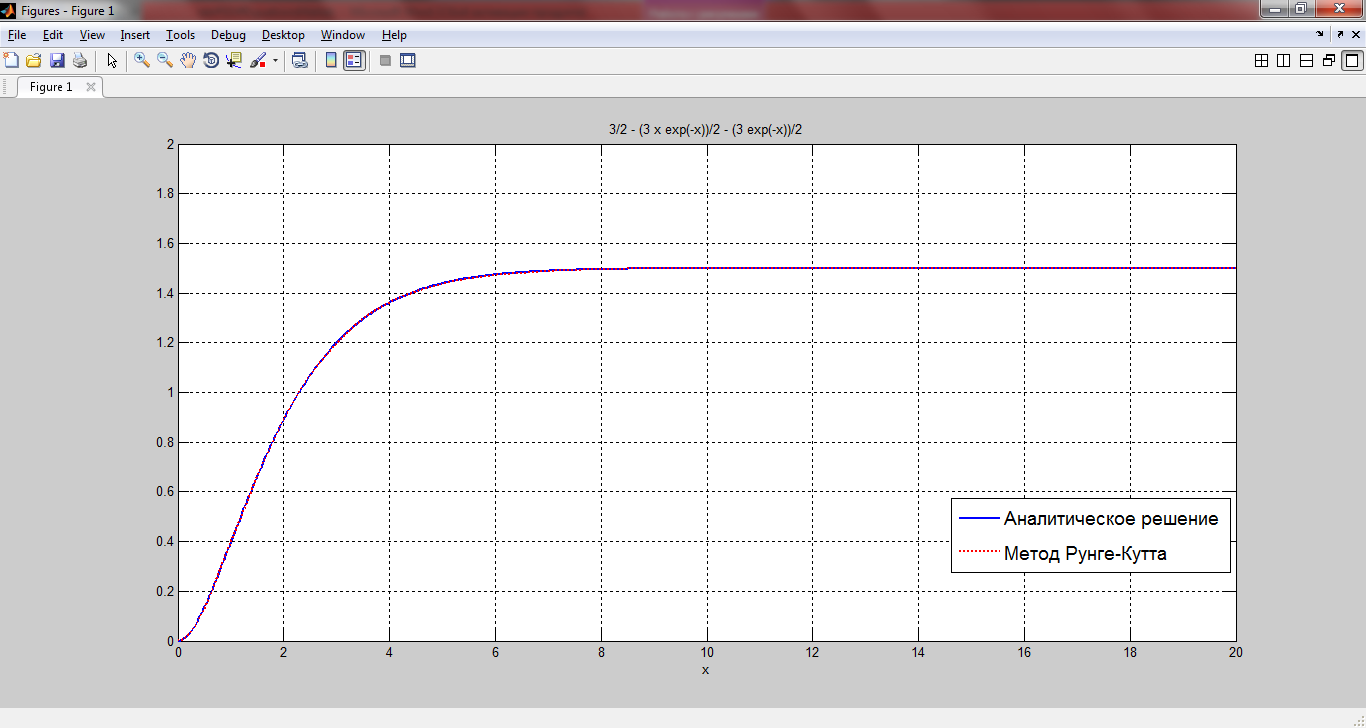 Решение краевой задачи также найдем аналитически через функцию dsolve() и с помощью методов bvp4c() и ode45(). %Аналитическое решение Y = dsolve('D2y+2*Dy+y=1.5', 'y(0)= 1', 'Dy(5)=6.5', 'x') y = ezplot(Y, [0,20]); %изображение графика символьного выражения set(y, 'LineWidth', 2); %установка толщины линии axis([0 20 -100 50]); %задание границ графика grid on; %создание сетки на графике hold on; %следующий график будет рисоваться в этом же окне Для того чтобы решить уравнение с помощью ode45(), необходимо знать начальные условия. Для нахождения начальных условий по граничным условиям можно воспользоваться функцией bvp4c(). function res = boundCon( ya, yb ) %Функция, вычисляющая разность между значением в граничной точке % и точным значением res = [ya(1) - 1 yb(2) - 6.5]; end %Задаем стартовые значения для поиска начальных условий solinit = bvpinit(linspace(0,5), [1 1]); %Нахождение значений y(x) и y'(x) на интервале [0;5] sol = bvp4c(@dy2, @boundCon, solinit); ystart2 = sol.y(2,1) %Начальные условия y0 = [1, ystart2]; interval = [0, 20]; [X,Y] = ode45(@dy2, interval, y0); %Значения искомой функции находятся в первом столбце матрицы Y plot(X, Y(:,1), ':r', 'LineWidth', 1.5) %изображение графика функции legend('Аналитическое решение','Метод Рунге-Кутта');  Графики решений полностью совпали. Изобразим фазовый портрет системы. Для этого решим ее с помощью функции ode45() при различных начальных условиях. %Интервал, на которм будет находится решение interval = [0, 20]; %Начальное условие y0 = [0, 0]; [X,Y] = ode45(@dy2, interval, y0); %Значения функции y(x) находятся в первом столбце %Значения производной y'(x) находятся во втором столбце plot(Y(:,1), Y(:,2), 'r', 'LineWidth', 2) grid on; %создание сетки на графике hold on; %Начальное условие y0 = [2, 1]; [X,Y] = ode45(@dy2, interval, y0); plot(Y(:,1), Y(:,2), 'r', 'LineWidth', 2) hold on; %Начальное условие y0 = [2, 1]; [X,Y] = ode45(@dy2, interval, y0); plot(Y(:,1), Y(:,2), 'b', 'LineWidth', 2) hold on; %Начальное условие y0 = [0.8, -0.5]; [X,Y] = ode45(@dy2, interval, y0); plot(Y(:,1), Y(:,2), 'r', 'LineWidth', 2) hold on; %Начальное условие y0 = [1.5, 1]; [X,Y] = ode45(@dy2, interval, y0); plot(Y(:,1), Y(:,2), 'b', 'LineWidth', 2) 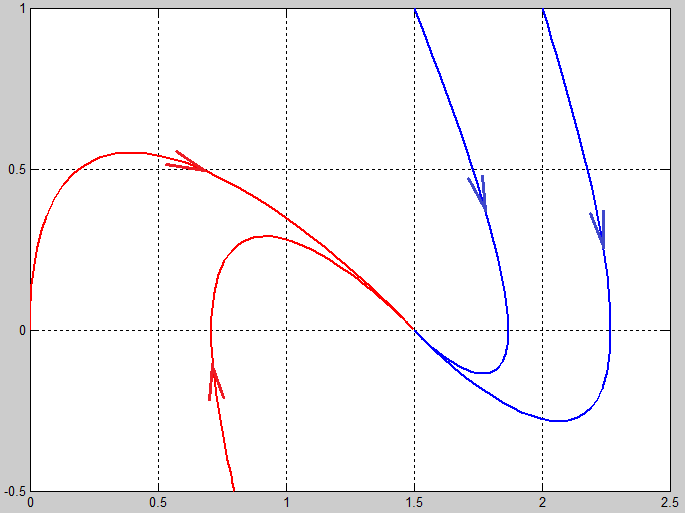 |
