Вариант 9 (Восстановлен). Решение. Найдем общее решение однородного дифференциального уравнения, соответствующего неоднородному уравнению (1) (2)
 Скачать 38.97 Kb. Скачать 38.97 Kb.
|
 1. Найти общее решение дифференциального уравнения первого порядка 1. Найти общее решение дифференциального уравнения первого порядкаy´+ y = 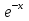 (1) (1)Решение. Найдем общее решение однородного дифференциального уравнения, соответствующего неоднородному уравнению (1): 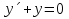 (2) (2)Запишем 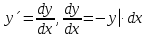 . Получаем . Получаем 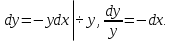 Проинтегрируем обе части уравнения: 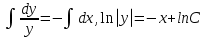 , где С=const. , где С=const.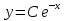 - общее решение уравнения (2). - общее решение уравнения (2).В уравнение (1) вместо y подставим 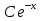 , допустив, что С - некоторая функция от х, т.е. , допустив, что С - некоторая функция от х, т.е. 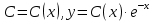 . .Получаем, 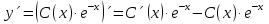 . .Подставляем в исходное уравнение: 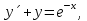 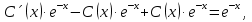 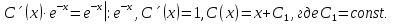 Итак, 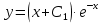 - общее решение уравнения (1). - общее решение уравнения (1).2. (19) Найти общее решение дифференциального уравнения второго порядка 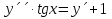 . (1) . (1)Решение. Уравнение (1) явно не содержит переменную y, значит допускает решить уравнение понижением степени производной. Заменим u = y´, тогда y´´ = u´ и уравнение принимает вид u´·tgx = u + 1, а это уже уравнение 1-й степени. Решим его: 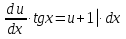 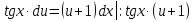 Вспомним, что tgx = 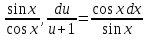 . .Проинтегрируем 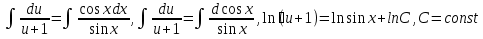 . .Отсюда 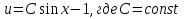 . .Вспомним, что u = y´, 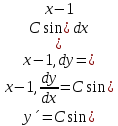 Проинтегрируем, 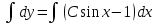 , , 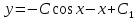 , где С и С1 = постоянные. , где С и С1 = постоянные.3. (39)Найти частное решение дифференциального уравнения 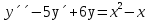 , удовлетворяющее начальным условиям , удовлетворяющее начальным условиям 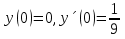 . .Решение. Запишем соответствующее однородное уравнение 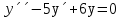 , характеристическое уравнение имеет вид , характеристическое уравнение имеет вид 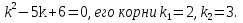 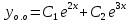 . .Так как правая часть уравнения представляет собой многочлен второй степени, то частное решение будем искать в виде 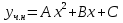 , , 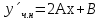 , , 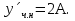 Подставим выражения для 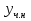 , , 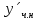 , , 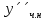 в исходное уравнение: в исходное уравнение: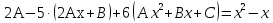 , ,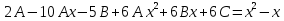 , ,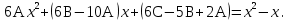 Приравниваем коэффициенты левой и правой частей и находим A, B и C: 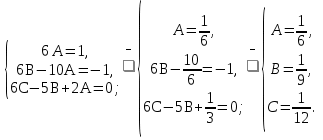 Отсюда, 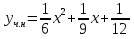 и и 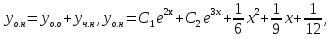 где С1 и С2 - некоторые постоянные. где С1 и С2 - некоторые постоянные.Теперь найдем частное решение, удовлетворяющее начальным условиям 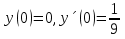 . .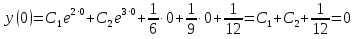 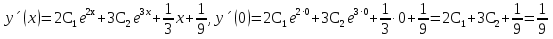 Получаем систему линейных уравнений относительно переменных C1 и С2: 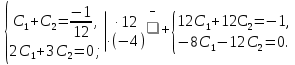 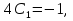 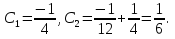 Ответ: 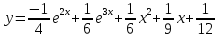 - частное решение дифференциального уравнения с заданными начальными условиями. - частное решение дифференциального уравнения с заданными начальными условиями.4.(49) Дана система линейных дифференциальных уравнений с постоянными коэффициентами 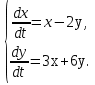 Требуется: 1) Найти общее решение системы с помощью характеристического уравнения; 2) записать в матричной форме систему и ее решение. Решение. 1) Запишем характеристическое уравнение: 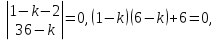 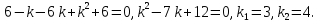 Значит общее решение системы дифференциальных уравнений имеет вид: Значит общее решение системы дифференциальных уравнений имеет вид: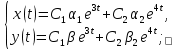 где С1 и С2 - некоторые постоянные. где С1 и С2 - некоторые постоянные.Найдем коэффициенты 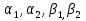 . .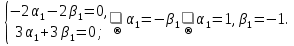 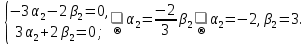 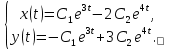 - общее решение системы дифференциальных уравнений. - общее решение системы дифференциальных уравнений.2) Запишем матрицу системы линейных уравнений 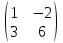 и матрицу неизвестных и матрицу неизвестных 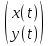 тогда система уравнений имеет вид: тогда система уравнений имеет вид: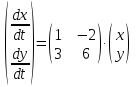 , а ее общее решение , а ее общее решение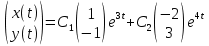 . .5 (59) Найти уравнение кривой, проходящей через точку А(-1;1) и обладающей тем свойством, что отрезок, отсекаемый на оси Ох касательной, проведенной в любой точке кривой, равен квадрату абсциссы точки касания. Решение. Пусть кривая задана уравнением y=f(x). Тогда уравнение касательной имеет вид: y=f(x0)+f´(x0)(x-x0). Отрезок, который эта кривая отсекает от оси Ох: 0= f(x0)+f´(x0)(x-x0). Отсюда найдем х (длину отрезка): f´(x0)(x-x0)= - f(x0), f´(x0)x- f´(x0)x0= - f(x0), f´(x0)x= f´(x0)x0 - f(x0), 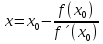 . .По условию 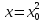 , т.е. , т.е. 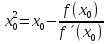 , , 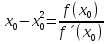 , ,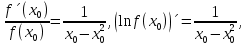 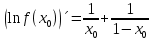 . .Проинтегрируем обе части: 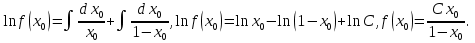 По условию при x=-1, y=1. 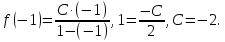 Итак, искомая функция имеет вид: 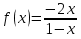 6 (69) Исследовать ряд на сходимость: а) 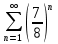 ; ;Решение. Применим признак Даламбера и найдем 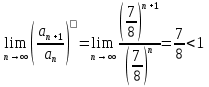 , значит ряд сходится. , значит ряд сходится.б) 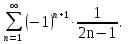 Решение. Данный ряд является знакочередующимся. Применим признак Лейбница: 1) 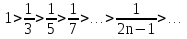 и 2) и 2) 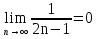 . .Следовательно ряд сходится. Рассмотрим ряд 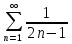 , состоящий из , состоящий из 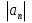 исходного ряда. Сравним его с расходящимся гармоническим рядом исходного ряда. Сравним его с расходящимся гармоническим рядом 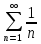 используя предельный признак сравнения: используя предельный признак сравнения: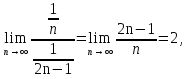 значит ряд значит ряд 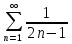 расходится и ряд расходится и ряд 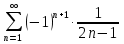 сходится условно. сходится условно.7 (79) Найти область сходимости степенного ряда 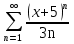 . .Решение. Найдем 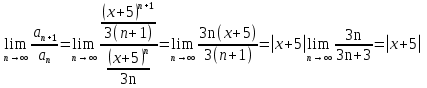 . .Чтобы ряд сходился необходимо, чтобы выполнялось условие 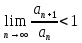 , т.е. , т.е. 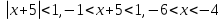 . .(-6;-4) - интервал сходимости. Рассмотрим этот ряд на концах интервала и выясним его сходимость. При х = - 6 получаем 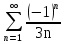 знакочередующийся ряд. знакочередующийся ряд.Применим признак Лейбница: 1) 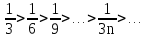 ; 2) ; 2) 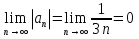 следовательно ряд сходится. следовательно ряд сходится.Рассмотрим ряд 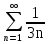 состоящий из модулей членов знакочередующегося ряда состоящий из модулей членов знакочередующегося ряда 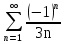 . .Сравним его с расходящимся гармоническим рядом 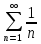 , используя предельный признак сравнения: , используя предельный признак сравнения: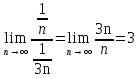 значит ряд значит ряд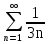 расходится. расходится.Ряд 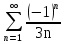 сходится условно. сходится условно.При х = -4 получаем 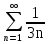 . Он расходится как мы уже выяснили. . Он расходится как мы уже выяснили.Ответ: (-6;-4) - интервал сходимости степенного ряда, при х= - 6 ряд сходится условно. 8. (89) Вычислить с помощью рядов (точность до 0,001): а) 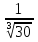 . .Решение: Преобразуем 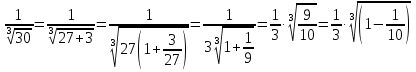 . .Теперь применим биномиальное разложение 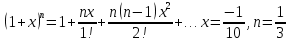 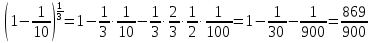 . .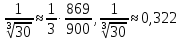 . .б) 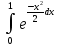 . .Решение. Используем табличное разложение 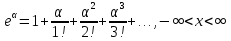 В нашем случае 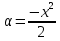 . Получаем . Получаем 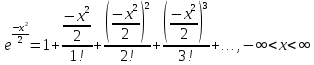 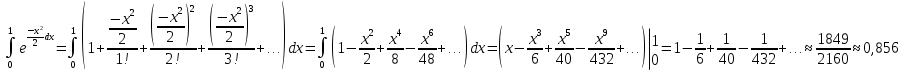 9. (99) Найти 4 первых члена разложения в степенной ряд решения дифференциального уравнения 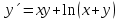 , удовлетворяющего начальным условиям y(1) = 0. , удовлетворяющего начальным условиям y(1) = 0.Решение. Разложение решения дифференциального уравнения в ряд выглядит так: 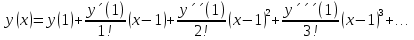 Начальное условие y(1) = 0 дает первый член этого ряда. Подставим х=1, у=0 в уравнение: 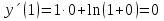 . И второй член этого ряда также равен 0. . И второй член этого ряда также равен 0.Продифференцируем исходное уравнение: 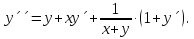 Найдем 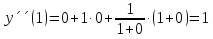 . .Найдем 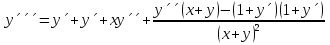 . . 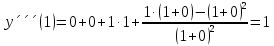 . .Подставим найденные значения в ряд, получим: 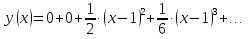 . .10. Разложить в ряд Фурье периодическую функцию с периодом 2l, заданную на промежутке (-l;l] следующими равенствами: f(x)=2x, -1<x≤1, l=1. Решение. Функция f(x)=2x является нечетной, поэтому коэффициенты аn=0 и функция раскладывается в ряд Фурье только по синусам: 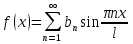 . .Найдем 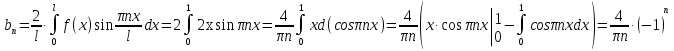 Таким образом 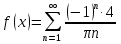 . . |
