теомех. Лек 12 Механикалы озалыс деп уаыт згерісінде кеістікте денені баса денелерге атысты орын ауыстыруын айтамыз. Кушматериялык денелердин озара асерлесуинин механикалык олшеуиши ретинде алынатын шама.
 Скачать 29.04 Kb.
|
|
лек 1-2 1. Механикалық қозғалыс деп уақыт өзгерісінде кеңістікте дененің басқа денелерге қатысты орын ауыстыруын айтамыз. 2. Куш-материялык денелердин озара асерлесуинин механикалык олшеуиши ретинде алынатын шама.Куштин катты денеге асери келесидей параметрлер аркылы сипатталады. Әрбір дене белгілі бір өлшемдерге ие. Дененің әр түрлі бөліктері кеңістіктің әр түрлі жерлерінде орналасады. Берілген есептің шартында дененің өлшемі мен формасын ескермеуге болатын денені материалдық нүкте деп атайды. Мәселен, оны ғаламшарлардың Күннің айналасындағы қозғалысын зерттегенде алуға болады. Бұл нәрсе деформацияланбайды, айнала алмайды. Материалдық нүктенің механикалық энергиясы тек қана оның кинетикалық энергиясы түрінде ғана жинақтала алады. Басқаша айтқанда, материалдық нүкте ең қарапайым механикалық жүйе; ең аз еркіндік дәрежесі бар механикалық жүйе. Абсолют қатты дене – ешбір жағдайларда да деформацияланбайтын дене және барлық жағдайларда да бұл дененің екі нүктесінің немесе екі бөлшегінің арақашықтығы өзгеріссіз қалады. Механикалық система динамикасы – әрбір нүктенің орны мен F – берілген күш, өлшем Н (1 Н күш массасы 1 кг нүктеге 1 м/c2 үдеу Механикалық системаның динамикасы 3. Теориялық механика - механикалық жүйенің қозғалыс заңдары және осы қозғалыстардың ортақ қасиеттерін қарастыратын механика бөлімі. Теориялық механика деп вакуумдағы жарық жылдамдығынан аз жылдамдықпен қозғалатын макроскопиялық денелердің қозғалысын зерттейтін Ньютонның классикалық механикасын түсінеді. Теориялық механика статика, кинематика және динамика бөлімінен кұралады 4.Статика негизине адамзаттын гасырлар бойы жиган тажирибесинин натижесинде тужырымдалып,математикалык далелдеуди кажет етпейтин аксиомага айналган зандылыктар жатады. Осы аксиомалар статикада карастырылгатын барлык маселелерди корытып шыгаруга абден жеткиликти. 1)аксиома(С1)-Кандай тузу болмасын,ол тузуде жататын нуктелер де,жатпайтын нуктелер де болады. 2)аксиома(С2)-Бир тузуде жатпайтын кез келген уш нукте аркылы бир гана жазыктык жургизуге болады. 3)аксиома(С3)-Егер тузудин еки нуктеси жазыктыкта жатса,онда тузу тутасымен осы жазыктыкта жатады. 4)аксиома(С4)-Егер артурли еки жазыктыктын ортак нуктеси бар болса,онда жазыктыктар осы нукте аркылы отетин тузу бойымен киылысады. Лек 3-4 1.Кеңістікте кез келген бағытта қозғалыс жасай алатын денені еркін дене деп атадық. Егер дене кейбір бағыттарда қозғалыс жасай алмайтын болса, онда ол еркін емес дене деп аталады. 2 Дене қозғалысының еркінділігін шектейтін шарттарды байланыстар деп атаймыз Байланыс ролін атқаратын дене берілген денеге бір күшпен қарсы әсер етеді де оның қозғалысын шектейді. Бұл күшті байланыс реакциясы дейміз.. Статика есептерінде кездесетін байланыстарды негізгі төрт түрге бөлуге болады: 1). Денелердің өзара түйісуі; 2). Денелерді топсалармен байланыстыру; 3). Сырықтар және иілгіш байланыстар; 4). Қазықша байланыстар. Лек 5-6 1. А 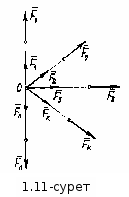 бсолют қатты дененің  нүктелеріне, әсер ету сызықтары бір О нүктесінде қиылысатын,  күштері түсірілсін дейік (1.11-сурет).Мұндай күштер жиынтығы жинақталатын күштер жүйесі деп аталады. 2..Тең әсерлі күш – денеге әсер ететін күш жүйелерінің әсеріне тең эквивалентті күш. 3. Жинақталатын күштер жүйесі тепе-теңдікте болуы үшін жүйе күштерінен құрылатын көпбұрыш тұйық болуы қажет және жеткілікті. 4. Егер қатты денеге әсер етіп тұрған өзара параллель емес үш күштің жазық жүйесі тепе-теңдікте болса, онда бұл күштердің әсер ету сызықтары бір нүктеде қиылысады. Лек 7-8 1. Қос күш– қатты денеге әсер ететін, шамалары тең, бағыттары қарама-қарсы , өзара параллель екі күштің жүйесі . Қос күш өзі түскен денені айналдыруға тырысады. Оның тең әсерлі күші болмайды. Күш моменті — күштің әсер ету сызығынан күш әрекеті қарастырылатын өске дейінгі ара кашықтығымен күштің көбейтіндісіне тең шама Қос күш моменті деп модулі, оның күші мен иінінің көбейтіндісіне (F h) тең, ал бағыты қос күш жазықтығына перпендикуляр болып келетін векторды айтамыз. 2. Күштердің жазық жүйесі  берілген жағдайда тепе-теңдік шарттары мына түрде алынады:  Мұндағы О күштер жатқан жазықтықтың кез келген бір нүктесі. Екі теңдеу күштердің кез келген жазық жүйесінің векторлық тепе-теңдік теңдеулерін өрнектейді. Осы теңдеулерден жазық жүйенің скаляр теңдеулермен берілетін теп-теңдік шарттарын алуға болады. Олар әр түрлі теңдеулер арқылы өрнектеледі Күштердің кез келген жазық жүйесінің тепе-теңдікте болуы үшін, ондағы барлық күштердің бір түзу бойында жатпайтын қандайда үш нүктенің әрқайсысына қатысты алынған моменттерінің қосындылары нөлге тең болулары қажет жіне жеткілікті:    |