3. Конспект лекций. Лекци и по дисциплине Эксплуатационные свойства автомобилей и безопасность движения
 Скачать 2.17 Mb. Скачать 2.17 Mb.
|
|
3. Устойчивость автомобиля 3.1 Продольное опрокидывание автомобиля Для неподвижного автомобиля сумма проекций внешних сил на любую ось и сумма моментов сил относительно любой оси равна нулю. Это позволяет составить нужное число уравнений и найти формулы для неизвестных величин. Проекцию PO силы P на ось находят по косинусу угла между осью и вектором силы P: PO = P cos (). Рассмотрим устойчивость автомобиля, стоящего на подъеме (рис. 3.1). Обозначим угол подъема в радианах. Разложим силу веса G на составляющие: GZ = G cos () и GX = G sin (), где: GZ , GX – нормальная и GX – продольная составляющие. 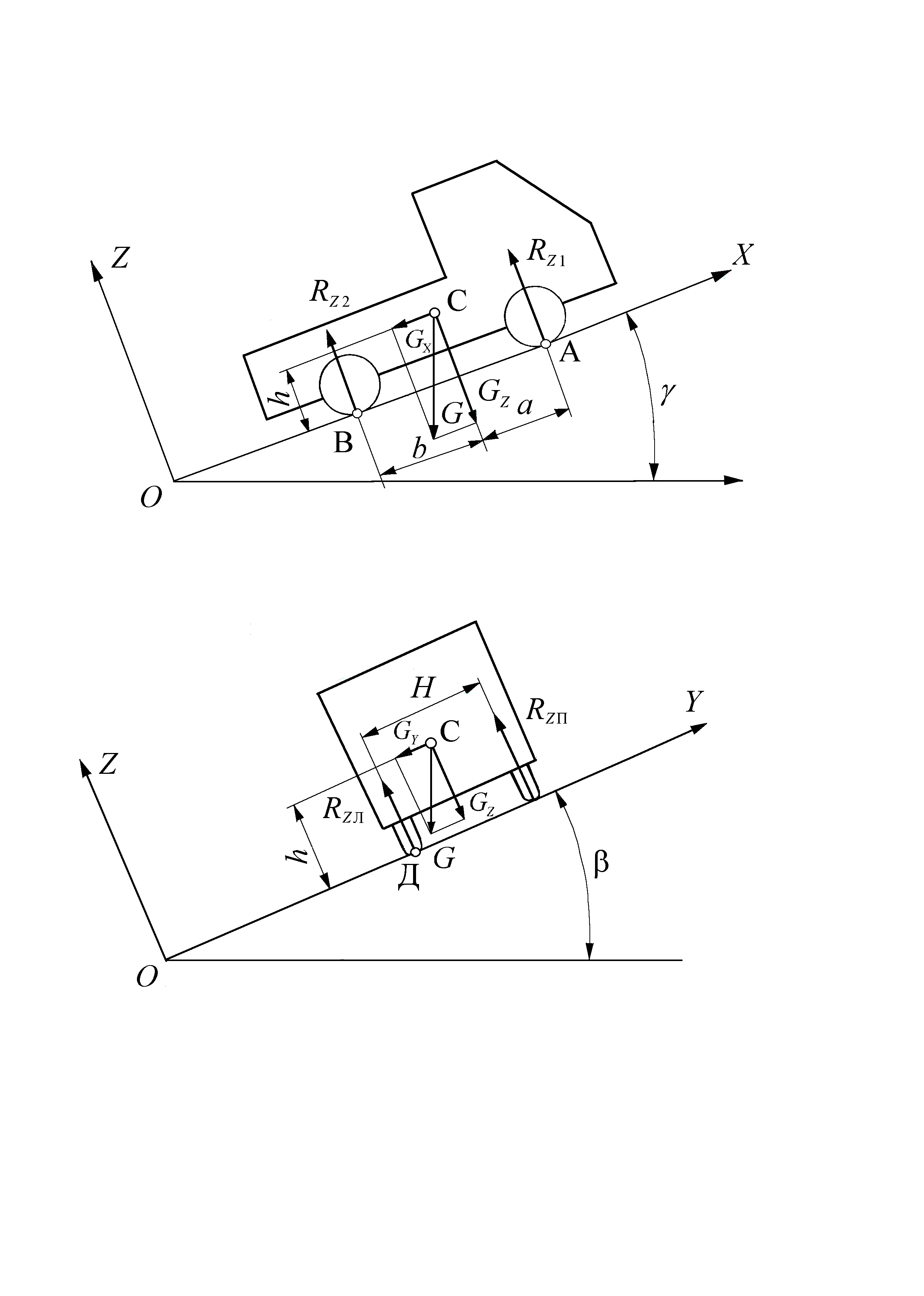 Рис. 3.1. Силы, действующие на неподвижный автомобиль на подъеме На подъеме нормальные нагрузки на переднюю и заднюю оси зависят от высоты h расположения центра масс автомобиля. Составляем суммы моментов сил относительно точек А и В: MA = GZ a + GX h – RZ2 L = G cos () a + G sin () h – RZ2 L = 0; MB = RZ1 L – GZ b + GX h = RZ1 L – G cos () b + G sin () h = 0. Получаем формулы: RZ1 = (G cos () b – G sin () h)/L; RZ2 = (G cos () a + G sin () h)/L. (17) При увеличении угла нагрузка возрастает на задней оси и снижается на передней оси. Найдем по первой формуле максимальный угол подъема МАХ, при котором автомобиль опрокинется относительно задней оси: RZ1 = cos() b – sin () h = 0: МАХ = arctg (b/h). (18) На уклоне ( < 0) может произойти опрокидывание автомобиля относительно передней оси. По второй формуле RZ2 =cos () a + sin () h = = 0 получаем: MIN = –arctg (a/h). (19) Пример. Возьмем снаряженный автомобиль ВАЗ-2101: a = 1,3 м, b = 1,1 м, h = = 0,55 м. Найдем критические значения углов подъема и уклона: МАХ = arctg (1,1/0,55) = arctg (2,0) = 64; МIN = –arctg (1,3/0,55) = –arctg (2,36) = –67. Рассмотрим устойчивость автомобиля, тормозящего на уклоне. На автомобиль действует сила инерции Pj, создаваемая тормозными силами. Она направлена против силы GX (см. рис. 3.1). Составим сумму моментов сил относительно точки A: MA = GZ a + GX h – RZ2 L – Pj h = = G cos () a + G sin () h – RZ2 L – Pj h = 0. Чтобы исключить путаницу, обозначим коэффициент интенсивности торможения символом т: Pj = т G. Найдем реакцию RZ2: RZ2 = G (a cos () + h sin () – т h)/L. (20) Опрокидывание автомобиля относительно передней оси произойдет при RZ2 =0: тмах = a cos ()/h + sin (), (21) где тмах – максимальная интенсивность торможения по условию опрокидывания. При торможении на уклоне нормальная реакция RZ колес автомобиля снижается: RZ = RZ1 + RZ2 = G cos (). Это ограничивает интенсивность торможения т cos () и снижает вероятность продольного опрокидывания. Пример. Возьмем снаряженный автомобиль ВАЗ-2101: a = 1,3 м, h = 0,55 м. Пусть = –45 = –0,785 рад. По формуле (56) получим: тмах = 1,3 0,71/0,55 – 0,71 = = 0,97. Чтобы получить т = 0,97, нужно иметь = 1,2/0,71 = 1,37. Следовательно, при экстренном торможении автомобиля ВАЗ-2101 на дороге с уклоном 45 не может произойти продольного опрокидывания автомобиля. 3.2 Устойчивость движения автомобиля на повороте Рассмотрим устойчивость автомобиля, стоящего на косогоре с углом (рис. 3.2). Силу веса G разлагаем на GZ – нормальную и GY – боковую – ее составляющие: GZ = G cos () и GY = G sin (). Расстояние между колесами левого и правого борта называют колеей. Пусть H – среднее расстояние между колесами левого и правого борта. Обозначим RZЛ – сумму нормальных реакций колес левого борта, RZП – правого. Составим сумму моментов сил относительно точки Д – центра контакта колес левого борта (см. рис. 3.2): MD = RZП H – GZ H/2 + GY h = 0; RZП H – G cos () H/2 + G sin () h=0. Находим RZП: RZП = G (H cos ()/2 – h sin ())/H. (22)  Рис. 3.2. Силы, действующие на неподвижный автомобиль на уклоне Составляем сумму проекций сил на ось OZ: PОZ= RZП + RZЛ – G= 0. Получаем RZП + RZЛ = GZ, и подставляем в это уравнение RZП из (58): RZЛ = G (cos ()/2 + h sin ()/H). По формуле (22) находим наибольший угол косогора МАХ, при котором произойдет поперечное опрокидывание автомобиля (RZП = 0): МАХ = arctg (H/(2h)). (23) Таким образом, анализируя распределение нагрузок на колеса автомобиля, мы нашли условия продольного или поперечного опрокидывания автомобиля. Пример. Возьмем снаряженный автомобиль ВАЗ-2101: Н = 1,3 м, h = 0,55 м. Найдем критический угол МАХ: МАХ = arctg (1,3/1,1) = arctg (1,18) = 50. Рассмотрим устойчивость автомобиля, движущегося на повороте известного радиуса Rп, по боковому заносу и опрокидыванию. К центру масс автомобиля приложена центробежная сила инерции PЦ = M V2/Rп, которая создается боковыми реакциями колес: PЦ = G. Отсюда легко найти критическую скорость Vкр движения автомобиля на повороте по условию бокового заноса при известном сцеплении шин с дорогой: Vкр = ( g Rп). (24) Составим сумму моментов сил относительно центра контакта колес правого борта, дальнего от центра поворота: M= G H/2 – RZЛ H– PЦ h= G H/2 – RZЛ H– h M V2/Rп= 0. Найдем критическую скорость Vкр по условию RZЛ = 0: Vкр = (Rп H g/(2h)). (25) Автомобили проектируют таким образом, чтобы критическая скорость на повороте по условию бокового заноса была меньше, чем по условию опрокидывания. Пример. Вычислим критическую скорость для снаряженного автомобиля ВАЗ-2101 на повороте радиуса 100 м при = 0,8: H = 1,3 м, h = 0,55 м: Vкр = ( g Rп) = (0,8 9,8 100) = 28 м/с =101 км/ч; Vкр = (Rп Hп g/(2h)) = (100 1,3 9,8/(2 0,55)) = 34 м/с =122 км/ч. Строители дорог изготавливают дорожное полотно с поперечным уклоном – углом . Это позволяет повысить скорость и безопасность движения. При движении на такой дороге на автомобиль действует горизонтальная центробежная сила инерции. Углы обычно малы по величине, что позволяет принять: cos () =1 и sin () = . Найдем критическую скорость Vкр движения автомобиля по условию бокового заноса. На автомобиль действует центробежная сила инерции PЦ = M V2/Rп. Она разлагается на две составляющие: PЦ sin () = PЦ – сила, перпендикулярная покрытию; PЦ cos () = PЦ – сила, параллельная покрытию. Первая составляющая увеличивает силу веса автомобиля: RZ = G cos () + PЦ sin () = G + PЦ . Вторая составляющая создается боковыми реакциями колес: PЦ = (G + PЦ ); PЦ = G/(1 – ); PЦ = M V2/Rп. Получаем формулу для скорости Vкр: Vкр = ( g Rп/(1 – )). (26) Из формулы следует: при движении на косогоре ( > 0) повышается критическая скорость по условию бокового заноса. Найдем критическую скорость Vкр по условию опрокидывания на косогоре. Для этого составим сумму моментов сил относительно центра контакта колес правого борта, дальнего от центра поворота: M= GZ H/2 – RZЛ H– PЦ h+ GY h = = G/(1 – ) H/2 – RZЛ H– M h V2/Rп + G h = 0. Отсюда находим критическую скорость Vкр по условию RZЛ = 0: Vкр = ( Rп g (H/(2h (1 – )) + )). (27) Из формулы следует: при движении на косогоре ( > 0) повышается критическая скорость по опрокидыванию. Пример. Вычислим снова критическую скорость для снаряженного автомобиля ВАЗ-2101 на повороте радиуса 100 м при = 0,8, на косогоре 10: H = 1,3 м, h = 0,55 м. Имеем = 0,17, находим по условию бокового заноса: Vкр = (0,8 9,8 100/(1 – 0,17)) = = (784/0,83) = 31 м/с =112 км/ч (увеличилась на 11%). Находим по условию опрокидывания: Vкр = (100 9,8 (1,3/(2 0,55 (1 – 0,17)) + 0,17)) = 39,5 м/с = 142 км/ч (увеличилась на 16%). 3.3 Устойчивость автомобиля при прямолинейном движении Прямолинейное движение автомобиля может быть неустойчивым: при постоянном угле поворота рулевого колеса наблюдается дрейф курсового угла – «автомобиль не держит дорогу». Причиной такой неустойчивости является избыточная поворачиваемость автомобиля. При этом не достигаются предельные по сцеплению боковые реакции колес, и не происходит опрокидывания. Рассмотрим причину дрейфа курсового угла автомобиля. Пусть при движении автомобиля на повороте случайно уменьшился радиус поворота Rп. Тогда угол увода 2 станет больше 1, центр поворота OП переместится вверх (см. рис. 2.3), радиус поворота станет еще меньше. Процесс уменьшения радиуса далее будет прогрессировать, и автомобиль выйдет за границы полосы движения. Дрейф может предотвратить водитель, если он вовремя уменьшит угол поворота управляемых колес. Очевидно: если этому не препятствуют другие транспортные средства. При избыточной поворачиваемости скорость движения автомобиля ограничена критической скоростью Vкр. Значение скорости Vкр находят из решения системы дифференциальных уравнений, описывающих боковое и вращательное движение автомобиля: Чем больше избыточная поворочиваемость – больше разница Y1 – Y2, тем меньше критическая скорость. Критическая скорость возрастает при увеличении базы L автомобиля. Сопротивление уводу шин зависит от нагрузок на оси автомобиля. Если увеличить нагрузку на заднюю ось, то коэффициент сопротивления уводу Y2 задней оси уменьшится (см. рис. 2.2). Автомобиль приобретет избыточную поворачиваемость. Если увеличить давление воздуха в шинах задней оси, то их сопротивление уводу уменьшится, снова получим избыточную поворачиваемость. Сопротивление шин уводу зависит от их нагруженности продольными реакциями: тяговыми или тормозными. При действии тяговых и тормозных сил снижается сопротивление шин уводу. У автомобиля с приводом на заднюю ось тяговые силы уменьшают сопротивление уводу колес этой оси и способствуют образованию избыточной поворачиваемости. У автомобиля с приводом на переднюю ось тяговые силы способствуют образованию недостаточной поворачиваемости. Поэтому переднеприводные автомобили более устойчивы. 3.4 Устойчивость автомобиля при торможении При расследовании ДТП часто приходится рассматривать торможение автомобиля, когда на него действуют боковые силы. Устойчивость автомобиля при торможении определяется характеристиками его шин. Сначала рассмотрим торможение автомобиля юзом, когда все его колеса скользят. При скольжении колесо не вращается, контакт шины скользит по дороге. В таком режиме реакция R колеса направлена против скорости Vс скольжения контакта (рис. 3.3), равной скорости центра колеса. Величина реакции определяется коэффициентом сцепления Б шины в режиме скольжения (юз): R = Б PZ, где PZ – нормальная нагрузка на колесо. Реакцию разлагаем на продольную и боковую ее составляющие: RX и RY (см. рис. 3.3). Реакции RX снижает скорость VCX автомобиля в продольной плоскости, а реакция RY – скорость VCY в поперечной плоскости. Обычно протектор шины имеет несимметричный рисунок в указанных плоскостях и коэффициент сцепления XБ отличается от YБ. При повороте колеса на угол увода реакция R описывает эллипс, который называют эллипсом трения. Однако при расследовании ДТП обычно нет данных об фактических значениях XБ и YБ, и принимают XБ = YБ. 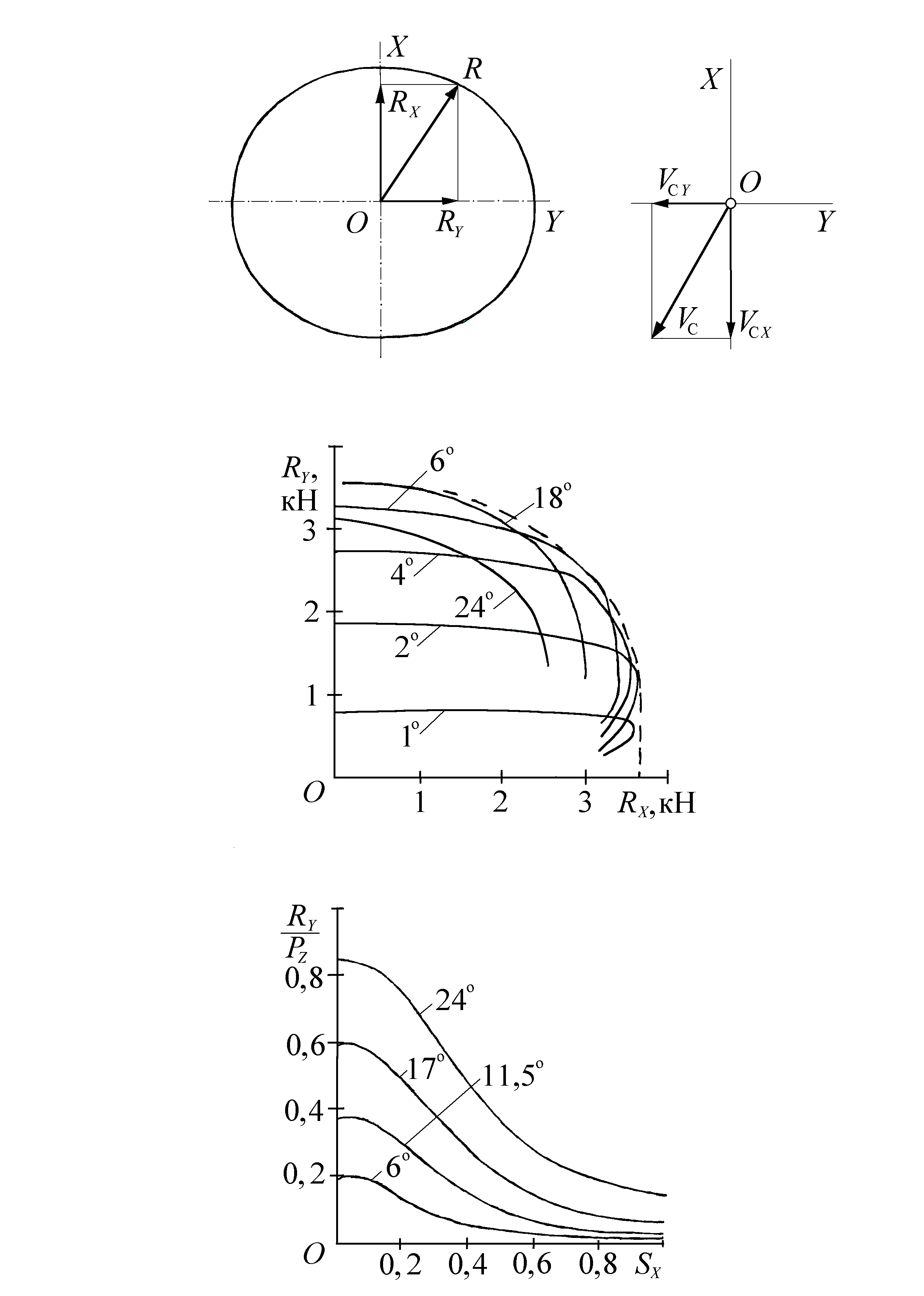 Рис. 3.3. Распределение реакций при скольжении колеса (юз) При торможении юзом реакция R направлена против скорости Vс и не зависит от угла увода колеса. При повороте управляемых колес направление реакции R не изменяется. Следовательно, автомобиль не реагирует на поворот руля и становится неуправляемым. Например, при торможении юзом на повороте автомобиль будет двигаться по касательной к окружности, удержать его в пределах круговой полосы движения невозможно. При торможении на уклоне на автомобиль действует внешняя боковая сила, которая уменьшает величину его бокового замедления. Скорость автомобиля в продольной плоскости теперь снижается до нуля раньше, чем его скорость в поперечной плоскости. В конце процесса торможения автомобиль начинает скользить в боковом направлении: образуется боковой занос автомобиля. Теперь рассмотрим торможение автомобиля на повороте без скольжения колес, когда они вращаются с тормозным проскальзыванием s < sK. При небольших углах увода (1…4) тормозная реакция RX почти не влияет на боковую реакцию RY (рис. 3.4). Автомобиль сохраняет устойчивость и остается управляемым. При больших углах увода (более 6) действие тормозной реакции сопровождается заметным снижением боковой реакции (см. рис. 3.4). Радиус поворота автомобиля увеличивается. Управляемость автомобиля сохраняется, и водитель, поворачивая рулевое колесо, может удержать автомобиль в заданной полосе движения. 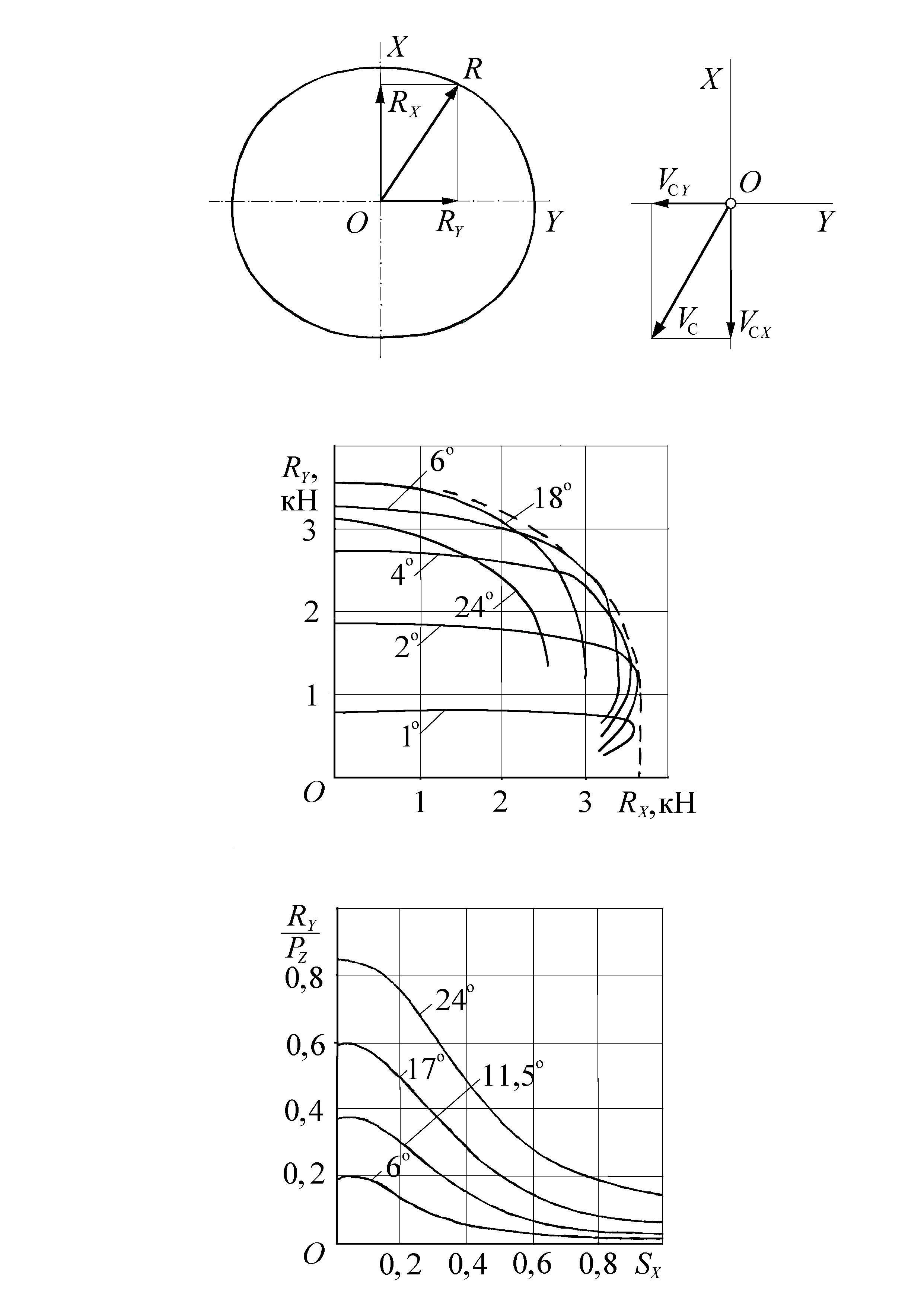 Рис. 3.4. Распределение реакций тормозящего колеса при различных углах увода: шина 205/70R14 на покрытии с высоким сцеплением Рассмотрим экстренное торможение автомобиля на повороте, когда колеса вращаются с проскальзыванием s sK. При достижении критического проскальзывания образуется максимальная тормозная реакция RX (см. рис. 3.4, кривые для углов 1 и 2). Боковая реакция RY снижается, но ее величина еще достаточна для обеспечения движения автомобиля на повороте. Автомобиль остается управляемым. Суммарная реакция R также ограничена эллипсом трения (на рис. 3.4 показана пунктиром). Размеры эллипса определены теперь коэффициентами сцепления X и Y. При расследовании ДТП обычно принимают X = Y. Водитель не может выдержать торможение автомобиля с проскальзыванием колес равным sK. Чтобы предотвратить юз колес, применяются АБС. Система АБС поддерживает вращение колес с некоторым проскальзыванием s < 1. При увеличении проскальзывания s боковая реакция колеса быстро снижается (рис. 3.5). Однако, при любом значении s < 1 реакция RY больше ее значения при скольжении (см. значения RY на рис. 3.5 при s = 1). В контакте шины реализуются значительные боковые реакции, если s < 0,3.  Рис. 3.5. Зависимости боковой реакции колеса от тормозного проскальзывания при различных углах увода на покрытии с высоким сцеплением При торможении с АБС, не смотря на увеличение радиуса поворота, автомобиль сохраняет устойчивость и остается управляемым. Рекомендуемая литература Основная: 1. Конструкция и расчет потребительских свойств автомобилей: Учебное пособие. / А.И. Федотов, А.М. Зарщиков. Иркутск. 2007. 334 с. 2. Вахламов В.К. Автомобили: Эксплуатационные свойства. Учебник для студентов высших учебных заведений. /М: Издательский центр «Ака-демия», 2005. – 240 с. 3. Теория автомобиля. Курс лекций. /В.В. Селифонов, –М.: Гринлайт, 2009. – 208 с. Дополнительная: 1. Краткий автомобильный справочник./ Б.В. Кисленко и др. М.: НИИАТ, Автополис – плюс, 2007. – 582 с. 2. Вахламов В.К. Автомобили: Эксплуатационные свойства. Учебник для ВУЗов. –М.: Изд-во «Академия», 2005. – 234 с. 3. Краткий автомобильный справочник. НИИАТ, М.: Транспорт, 1984, 1994 и др. 4. Проектирование автомобилей: Методические указания к выполнению курсового проекта по дисциплинам «Техника транспорта» и «Автомобили» для студентов специальностей 240400 и 150200 / Сост. В.Д. Балакин. – Омск : Изд - во СибАДИ, 2002. 5. Лабораторный практикум по теории автомобилей /Сост.: К.В. Зайцев, Л.Г. Ягодкин. – Омск: Изд-во СибАДИ, 2005. – 48 с. |
