Любанов дз2 оптимизация числа скважин. Лекции 3 Задание заключается в решении задачи
 Скачать 33.03 Kb. Скачать 33.03 Kb.
|
|
Любанов Даниил АСМ-22-05 Вариант 14 ДОМАШНЕЕ ЗАДАНИЕ № 2 (АСМ-22-05) «Оптимизация числа скважин» (по материалам лекции 3) Задание заключается в решении задачи: требуется найти такое число скважин и соответствующее этому числу значение конечной газоотдачи, которые обеспечит максимум прибыли от разработки залежи за весь период ее эксплуатации при выполнении ограничения на предельное значение газоотдачи. Исходными данными являются: - q0 – начальный дебит одной скважины; - T – срок разработки; - п – предельное значение газоотдачи; - V – геологические запасы залежи; - а – отпускная цена объемной единицы газа с учетом затрат на ее добычу; - b – суммарные затраты на строительство скважины и ее обслуживание за весь срок разработки. Для математической формулировки введем z – значение конечной газоотдачи (газоотдачи за весь срок разработки) и x – число скважин (целочисленностью х пренебрегается). С учетом введенных обозначений модель оптимизации числа скважин принимает вид задачи на условный экстремум по двум переменным z и х (см. семинар 6):  (1) (1)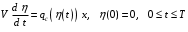 , (2) , (2)z=(T), (3) 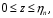 x 0. (4) x 0. (4)В задаче (1)-(4): F(z,x) – прибыль от разработки залежи за весть срок ее эксплуатации; - c – прочие затраты, независимые от числа скважин; - qc((t)) – зависимость дебита скважины от текущего значения газоотдачи; - (t) – зависимость газоотдачи от времени. ВНИМАНИЕ! Используя полученную на лекции 3 (размещена на портале) зависимость конечной газоотдачи от числа скважин (формула (26)): 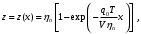 1) решить задачу (1)-(4) в общем виде, т.е. необходимо получить аналитическое решение в виде формулы (сначала для числа скважин, затем для газоотдачи), выражающие оптимальные значения числа скважин и конечной газоотдачи через исходные параметры; 2) определить оптимальные значения числа скважин и конечной газоотдачи, исходя из заданного набора исходных данных (см. ниже). Исходные данные 14 вариант (№ варианта совпадает с № магистранта в списке группы) Таблица 1 – Исходные данные по вариантам
1)Теоретическая часть с выводом формул: Из уравнения (2) находим x – искомое число скважин: x = 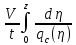 (5). (5).Интегрируя по времени и подставляя формулу (5) в уравнение (1), убираем константу c, не влияющую на оптимизацию, и получаем следующую формулу: f(z) = a*z - 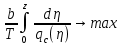 (6). (V, c - const) (6). (V, c - const)Посмотрим на уравнение (6) при условии z=0, f(z) = 0; Тогда при z 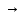 nn получим qc(z) nn получим qc(z) 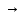 0; f(z) 0; f(z) 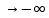 . .Найдём производную от f(z0) по z: 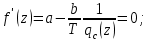 Получается: z* = 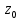 , при , при 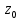 > 0; > 0;z*=0, при 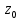 ≤ 0. ≤ 0.Тогда оптимальное число скважин: x*= 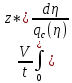 . .Допустим, что: qс((t))=q0(1-(t)/n). Тогда: 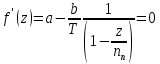 , ,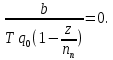 Посчитаем 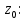 z0 = 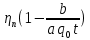 . .При 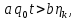 искомая z*= z0, иначе z*= 0. искомая z*= z0, иначе z*= 0.Выразим x* и получим решение задачи в общем виде: x* = 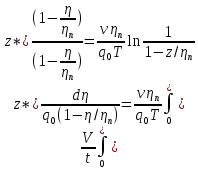 . .2)Расчётная часть со своими данными: Вычислим искомые значения, подставив неизвестные в формулы для z* и x*. Значение конечной газоотдачи: z* = 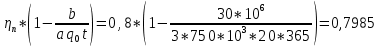 Число скважин: x* = 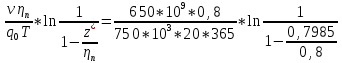 = 596,375569 = 596,375569Округлим до целого и получим: 597 скважин. |
