задание 2. Готовое задание 2 методы прин. упр. реш.. Лекции Задачи оптимизации при принятии решений
 Скачать 254.76 Kb. Скачать 254.76 Kb.
|
Задания1. Изобразите на плоскости ограничения задачи линейного программирования и решите (графически) эту задачу: 400W1 + 450W2 min 5W1 + 10W2 ≥ 45 20W1 + 15W2 ≥ 80 W1 ≥ 0, W2 ≥ 0 Решение: Построим область допустимых решений 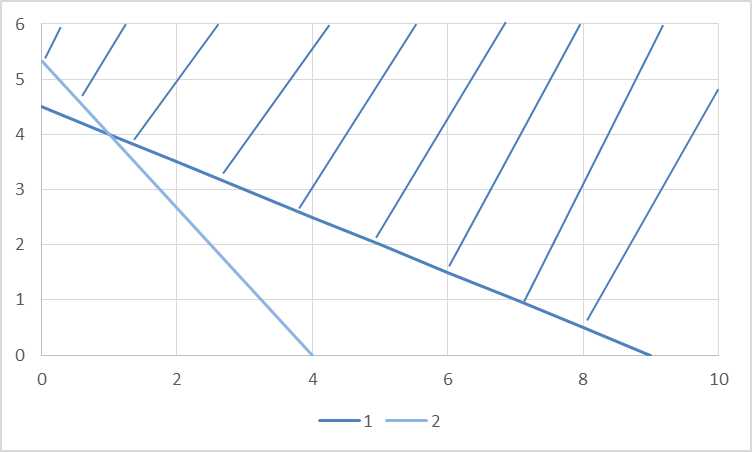 Построим целевую функцию 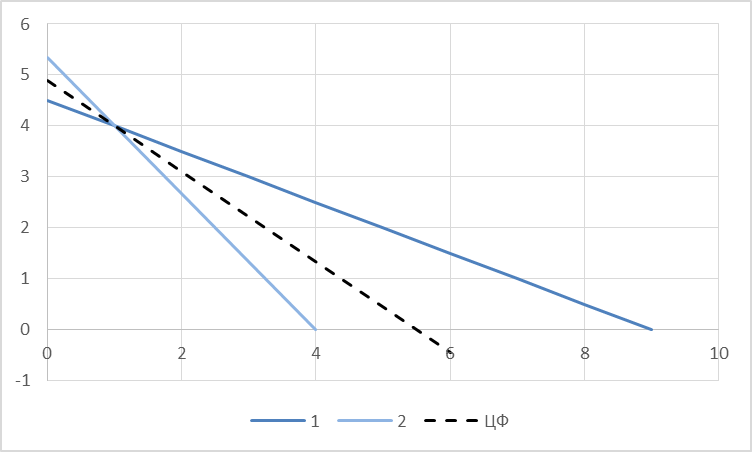 Точка минимума: 5W1 + 10W2 = 45 20W1 + 15W2 = 80 Отсюда W1 + 2W2 = 9 4W1 + 3W2 = 16 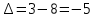 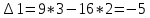 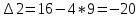 W1 =1;W2 = 4 Минимальное значение функции 400W1 + 450W2 = 400*1+450*4=2200 2. Решите задачу линейного программирования: W1 + 5W2 max 0,1W1 + W2 ≤ 3,8 0,25W1 + 0,25W2 ≤ 4,2 W1 ≥ 0, W2 ≥ 0 Решение: Данную задачу можно решать различными методами, так как переменных две, то наиболее простой вариант – используя графический метод. 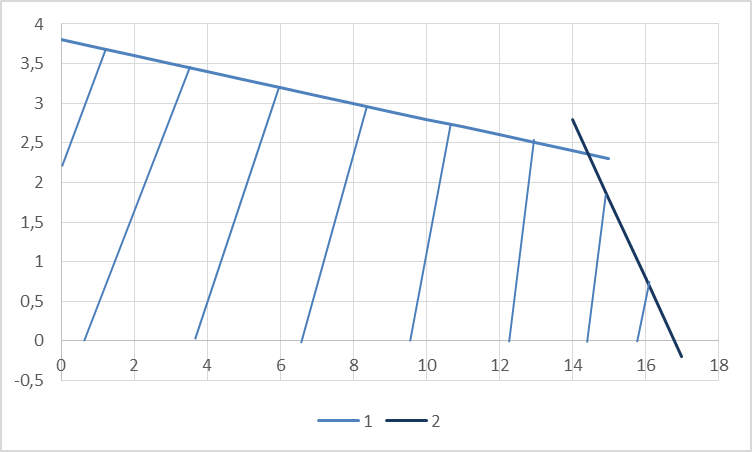 Нанесем целевую функцию 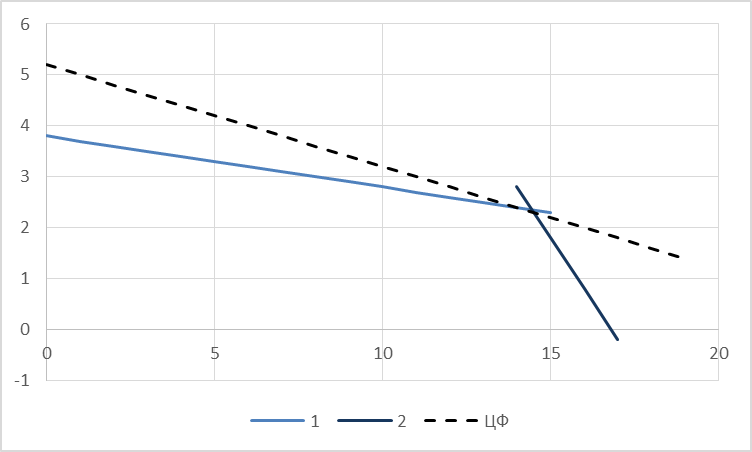 Максимальное значение в точке пересечения 0,1W1 + W2 = 3,8 0,25W1 + 0,25W2 = 4,2 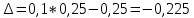 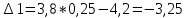 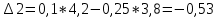 W1 =14,44;W2 = 2,36 Максимальное значение функции W1 + 5W2 =14,44+5*2,36=26,24 3. Решите задачу целочисленного программирования: 10X + 5Ymax 8X + 3Y ≤ 40 3X +10Y ≤ 30 X ≥ 0, Y ≥ 0 XиY - целые числа Решение: Решим задачу графически. 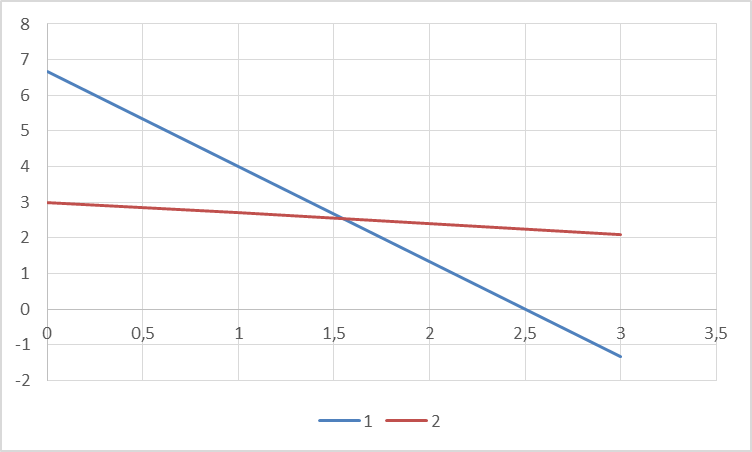 Нанесем целевую функцию 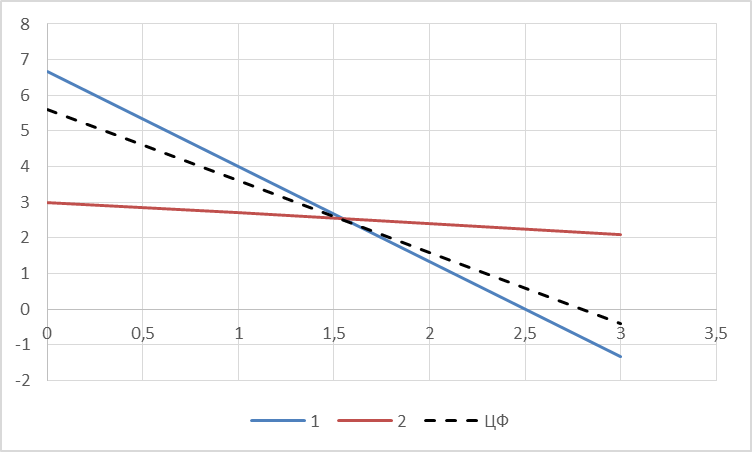 Получим решение: 8X + 3Y = 40 3X +10Y = 30 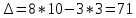 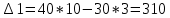 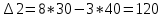 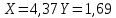 Решение получили не целочисленное, параллельным переносом найдем целочисленное решение. 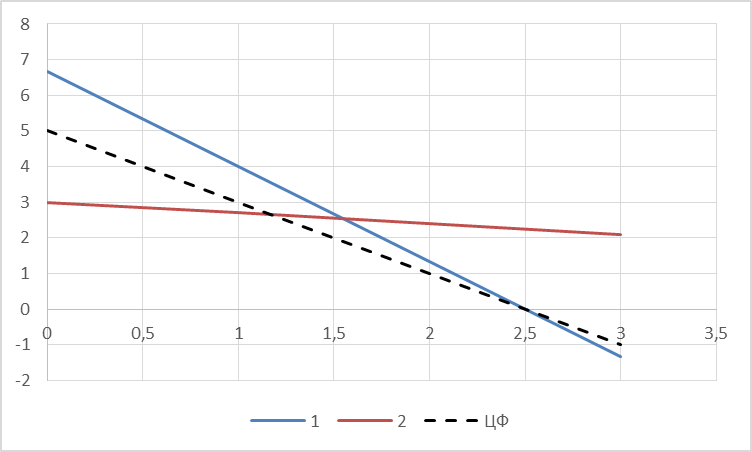 Получим целочисленное решение 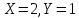 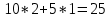 4. Решите задачу о ранце: X1 + X2 + 2X3 + 2X4 + X5 + X6max 0,5X1 + X2 + 1,5X3 + 2X4 + 2,5X5 + 3X6 ≤ 3 Управляющие параметры Xk, k=1,2,3,4,5,6, принимают значения из множества, содержащего два элемента - 0 и 1. Решение: Условная оптимизация. f6(L) = max(1x6); 0 < x6 < 1; x6 = 0,1. f6(0) = max[0*1] = 0 f6(1) = max[0*1] = 0 f6(2) = max[0*1] = 0 f6(3) = max[0*1, 1*1] = 1 Таблица 1 – Расчет значения функции f1(L)
f5(L) = max[1x5 + f6(L - 2.5x5)]; 0 < x5 < 1; x5 = 0,1. f5(0) = max[0*1+0] = 0 f5(1) = max[0*1+0] = 0 f5(2) = max[0*1+0] = 0 f5(3) = max[0*1+1, 1*1+0] = 1 Таблица 2 – Расчет значения функции f2(L)
f4(L) = max[2x4 + f5(L - 2x4)]; 0 < x4 < 1; x4 = 0,1. f4(0) = max[0*2+0] = 0 f4(1) = max[0*2+0] = 0 f4(2) = max[0*2+0, 1*2+0] = 2 f4(3) = max[0*2+1, 1*2+0] = 2 Таблица 3 – Расчет значения функции f3(L)
f3(L) = max[2x3 + f4(L - 1.5x3)]; 0 < x3 < 1; x3 = 0,1. f3(0) = max[0*2+0] = 0 f3(1) = max[0*2+0] = 0 f3(2) = max[0*2+2, 1*2+0] = 2 f3(3) = max[0*2+2, 1*2+0] = 2 Таблица 4 – Расчет значения функции f4(L)
f2(L) = max[1x2 + f3(L - 1x2)]; 0 < x2 < 1; x2 = 0,1. f2(0) = max[0*1+0] = 0 f2(1) = max[0*1+0, 1*1+0] = 1 f2(2) = max[0*1+2, 1*1+0] = 2 f2(3) = max[0*1+2, 1*1+2] = 3 Таблица 5 – Расчет значения функции f5(L)
f1(L) = max[1x1 + f2(L - 0.5x1)]; 0 < x1 < 1; x1 = 0,1. f1(0) = max[0*1+0] = 0 f1(1) = max[0*1+1, 1*1+0] = 1 f1(2) = max[0*1+2, 1*1+1] = 2 f1(3) = max[0*1+3, 1*1+2] = 3 Таблица 6 – Расчет значения функции f6(L)
Безусловная оптимизация. Таким образом, максимальный вес рюкзака f1(3) равна 3 кг. При этом x1 = 0, так как f1(3) = 3 достигается при х1=0 (см. таблицу 6). Предметы остальных типов распределяются следующим образом: L = 3 - 0.5 * 0 = 3 f2(3) = 3 достигается при х2 = 1 (см. таблицу 5). L = 3 - 1 * 1 = 2 f3(2) = 2 достигается при х3 = 0 (см. таблицу 4). L = 2 - 1.5 * 0 = 2 f4(2) = 2 достигается при х4 = 1 (см. таблицу 3). L = 2 - 2 * 1 = 0 f5(0) = 0 достигается при х5 = 0 (см. таблицу 2). L = 0 - 2.5 * 0 = 0 f6(0) = 0 достигается при х6 = 0 (см. таблицу 1). L = 0 - 3 * 0 = 0 В итоге наилучший вариант загрузки рюкзака достигается при значениях: x1 = 0, x2 = 1, x3 = 0, x4 = 1, x5 = 0, x6 = 0 5. Транспортная сеть (с указанием расстояний) приведена на рис. 8.9. Найдите кратчайший путь из пункта 1 в пункт 4. 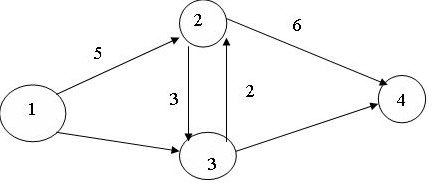 Рис. 8.9. Исходные данные к задаче о кратчайшем пути Решение: Проанализируем возможные варианты (1 – 2) = 5 (1 – 3) = 0 (1 – 3) + (1 – 4) = 0 Кратчайший путь – 0. 6. Как послать максимальное количество грузов из начального пункта 1 в конечный пункт 8, если пропускная способность путей между пунктами транспортной сети (рис. 8.10) ограничена (табл. 8.7)? 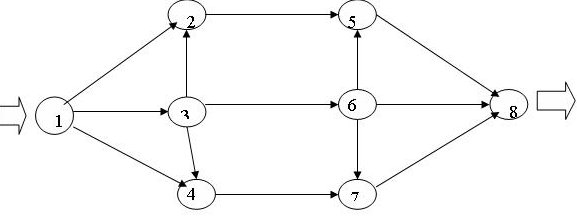 Рис. 8.10. Транспортная сеть к задаче о максимальном потоке Таблица 8.7 Исходные данные к задаче о максимальном потоке
Решение: Максимальная пропускная способность составит 1+2+3 = 6 единиц, так как из первого пункта возможно отправить только 6 единиц. Далее из пункта 4 все грузы (3) могут быть отправлены в пункт 7. Из пункта 3 один груз отправляем в пункт 6 и далее в пункт 8. Один груз из пункта 3 в пункт 4, оттуда в пункт 7. И остается один груз – из пункта 2 в пункт 5 и далее в пункт 8. Грузы, собранные в пункте 7 – 4 штуки – отправляем в пункт 8. Итак, максимальная пропускная способность рассматриваемой транспортной системы - 6 единиц груза. При этом не используются внутренние участки (ветки) между пунктами 3 и 2, 6 и 7. Большая часть веток не догружена. 7. Решите задачу коммивояжера для четырех городов (маршрут должен быть замкнутым и не содержать повторных посещений). Затраты на проезд приведены в табл. 8.8. Таблица 8.8 Исходные данные к задаче коммивояжера
Решение: Введем обозначение: С(Т) - длина кратчайшего пути из вершины 1 в вершину Т. (Поскольку любой путь, который надо рассмотреть, состоит из дуг, а дуг конечное число, и каждая входит не более одного раза, то претендентов на кратчайший путь конечное число, и минимум из конечного числа элементов всегда достигается.) Рассматриваемая задача состоит в вычислении С(Ф) и указании пути, на котором этот минимум достигается. В вершину Ф входит только один путь из вершины Д. То есть кратчайший пусть С(Д) + 5. Найдем кратчайший путь в вершину Д. Возможные варианты С(Д)=min (С(А) + 5; С(Б) + 1; С(В) + 2) Проанализируем пути С(А) = min (C(Б) + 3; С(В) + 4) С(Б) = min (С(А) + 2; С(В) + 1) С(В) = min (C(A) + 1; C(Б) + 2) Итак, путь А – В – Б – Д – Ф Длина пути составит 1+1+1+1+5=9 |
