задание 2. Готовое задание 2 методы прин. упр. реш.. Лекции Задачи оптимизации при принятии решений
 Скачать 254.76 Kb. Скачать 254.76 Kb.
|
8. ОПТИМИЗАЦИОННЫЕ ЗАДАЧИМетодические указанияТеоретический материал для выполнения практической работы изложен в лекции «Задачи оптимизации при принятии решений». Рассмотрим несколько типовых задач линейного программирования. Задача о диете (упрощенный вариант) . Предположим для определенности, что необходимо составить самый дешевый рацион питания цыплят, содержащий необходимое количество определенных питательных веществ (для простоты, тиамина Т и ниацина Н). Таблица 8.1 Исходные данные в задаче об оптимизации смеси
Пищевая ценность рациона (в калориях) должна быть не менее заданной. Пусть для простоты смесь для цыплят изготавливается из двух продуктов - К и С. Известно содержание тиамина и ниацина в этих продуктах, а также питательная ценность К и С (в калориях). Сколько К и С надо взять для одной порции куриного корма, чтобы цыплята получили необходимую им дозу веществ Н и Т и калорий (или больше), а стоимость порции была минимальна? Исходные данные для расчетов приведены в табл. 8.1. Задача линейного программирования имеет вид: 3,8K+4,2C min 0,10K+0,25C≥1,00 1,00K+0,25C≥5,00 110K+120C≥400,00 K≥0 C≥0 Ее графическое решение представлено на рис. 8.1 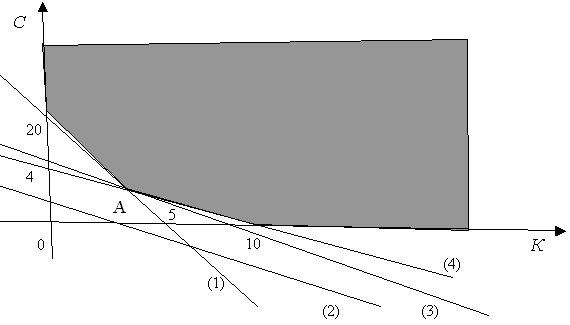 Рис. 8.41. Графическое решение задачи об оптимизации смеси На рис. 8.4 ради облегчения восприятия четыре прямые обозначены номерами (1) - (4). Прямая (1) описывается уравнением 1,00K+0,25C=5,00 (ограничение по веществу Н). Она проходит, как и показано на рисунке, через точки (5, 0) на оси абсцисс и (0, 20) на оси ординат. Обратите внимание, что допустимые значения параметров (К, С) лежат выше прямой (1) или на ней, в отличие от ранее рассмотренных случаев в предыдущей производственной задаче линейного программирования. Прямая (2) - это прямая 110K+120C=400,00 (ограничение по калориям). Обратим внимание, что в области неотрицательных С она расположена всюду ниже прямой (1). Действительно, это верно при K=0, прямая (1) проходит через точку (0, 20), а прямая (2) - через расположенную ниже точку (0, 400/120). Точка пересечения двух прямых находится при решении системы уравнений 1,00K+0,25C=5,00 110K+120C=400,00 Из первого уравнения K=5-0,25C. Подставим во второе: 110(5-0,25C)+120C=400, откуда 550-27,5C+120C=400. Следовательно, 150=-92,5C , т.е. решение достигается при отрицательном С. Это и означает, что при всех положительных С прямая (2) лежит ниже прямой (1). Значит, если выполнено ограничение по Н, то обязательно выполнено и ограничение по калориям. Мы столкнулись с новым явлением - некоторые ограничения с математической точки зрения могут оказаться лишними. С экономической точки зрения они необходимы, отражают существенные черты постановки задачи, но в данном случае внутренняя структура задачи оказалась такова, что ограничение по калориям не участвует в формировании допустимой области параметров и нахождении решения. Прямая (4) - это прямая 0,1K+0,25C=1 (ограничение по веществу Т). Она проходит, как и показано на рисунке, через точки (10, 0) на оси абсцисс и (0, 4) на оси ординат. Обратите внимание, что допустимые значения параметров (К, С) лежат выше прямой (4) или на ней, как и для прямой (1). Следовательно, область допустимых значений параметров (К, С) является неограниченной сверху. Из всей плоскости она выделяется осями координат (лежит в первом квадранте) и прямыми (1) и (4) (лежит выше этих прямых, а также включает граничные отрезки). Область допустимых значений параметров, т.е. точек (К, С), можно назвать "неограниченным многоугольником". Минимум целевой функции 3.8K+4,2C может достигаться только в вершинах этого "многоугольника". Вершин всего три. Это пересечения с осями абсцисс (10, 0) и ординат (0, 20) прямых (1) и (4) (в каждом случае из двух пересечений берется то, которое удовлетворяет обоим ограничениям). Третья вершина - это точка А пересечения прямых (1) и (4), координаты которой находятся при решении системы уравнений 0,10K+0,25C=1,00 1,00K+0,25C=5,00 Из второго уравнения K=5-0,25C, из первого 0,1(5-0,25C)+0,25C=5,00=0,25C=0,5+0,225C=1, откуда C=0,5/0,225=20/9 и K=5-5/9=40/9. Итак, A=(20/9,40/9). Прямая (3) на рис. 8.5 - это прямая, соответствующая целевой функции 3,8K+4,2C. Она проходит между прямыми (1) и (4), задающими ограничения, и минимум достигается в точке А, через которую и проходит прямая (3). Следовательно, минимум равен 3,8x40/9+4,2x20/9=236/9. Задача об оптимизации смеси полностью решена. Двойственная задача, построенная по ранее описанным правилам, имеет приведенный ниже вид (мы повторяем здесь и исходную задачу об оптимизации смеси, чтобы наглядно продемонстрировать технологию построения двойственной задачи): 3,8K+4,2C min W1+5W2+400W3 max 0,10K+0,25C ≥1,00 0,1W1+1,10W2+110W3≤3,8 1,00K+0,25C ≥5,00 0,25W1+0,25W2+120W3≤4,2 110K+120C ≥400,00 W1≥0 K ≥0 W2≥0 C ≥0 W3≥0 Минимальное значение в прямой задаче, как и должно быть, равно максимальному значению в двойственной задаче, т.е. оба числа равны 236/9. Интерпретация двойственных переменных: W1 - "стоимость" единицы вещества Т, а W2 - "стоимость" единицы вещества Н, измеренные "по их вкладу" в целевую функцию. При этом W3=0, поскольку ограничение на число калорий никак не участвует в формировании оптимального решения. Итак, W1,W2,W3 - это т.н. объективно обусловленные оценки (по Л.В. Канторовичу) ресурсов (веществ Т и Н, калорий). Планирование номенклатуры и объемов выпуска. Вернемся к организации производства. Предприятие может выпускать автоматические кухни (вид кастрюль), кофеварки и самовары. В табл. 8.2 приведены данные о производственных мощностях, имеющихся на предприятии (в штуках изделий). Таблица 8.2 Производственные мощности (в шт.)
При этом штамповка и отделка проводятся на одном и том же оборудовании. Оно позволяет штамповать за заданное время или 20000 кухонь, либо 30000 кофеварок, либо и то, и другое, не в меньшем количестве. А вот сборка проводится на отдельных участках. Задача линейного программирования имеет вид: X1 ≥ 0,X2 ≥ 0,X3 ≥ 0 (0) X1/200+X2/300+X3/120≤100 (1) X1/300+X2/100+X3/120≤100 (2) X1/200≤100 (3) X2/120≤100 (4) X3/80≤100 (5) F = 15X1 + 12X2 + 14X3 max. Здесь: (0) - обычное в экономике условие неотрицательности переменных, (1) - ограничение по возможностям штамповки (выраженное для облегчения восприятия в процентах), (2) - ограничение по возможностям отделки, (3) - ограничение по сборке для кухонь, (4) - то же для кофемолок, (5) - то же для самоваров (как уже говорилось, все три вида изделий собираются на отдельных линиях). Наконец, целевая функция Заметим, что неравенство (3) вытекает из неравенства (1), а неравенство (4) - из (2). Поэтому неравенства (3) и (4) можно из формулировки задачи линейного программирования исключить. Отметим сразу любопытный факт. Как будет установлено, в оптимальном плане X3 = 0, т.е. самовары выпускать невыгодно. Транспортная задача. Различные технико-экономические и экономические задачи производственного менеджмента, от оптимальной загрузки станка и раскройки стального листа или полотна ткани до анализа межотраслевого баланса и оценки темпов роста экономики страны в целом, приводят к необходимости решения тех или иных задач линейного программирования. В качестве очередного примера рассмотрим т.н. транспортную задачу. Имеются склады, запасы на которых известны. Известны потребители и объемы их потребностей. Необходимо доставить товар со складов потребителям. Можно по-разному организовать "прикрепление" потребителей к складам, т.е. установить, с какого склада какому потребителю и сколько вести. Кроме того, известна стоимость доставки единицы товара с определенного склада определенному потребителю. Требуется минимизировать издержки по перевозке. Например, может идти речь о перевозке песка - сырья для производства кирпичей. В Москву песок обычно доставляется самым дешевым транспортом - водным. Поэтому в качестве складов можно рассматривать порты, а в качестве запасов - их суточную пропускную способность. Потребителями являются кирпичные заводы, а их потребности определяются суточным производством (в соответствии с имеющимися заказами). Для доставки необходимо загрузить автотранспорт, проехать по определенному маршруту и разгрузить его. Стоимость этих операций рассчитывается по известным правилам, на которых не имеет смысла останавливаться. Поэтому затраты на доставку товара с определенного склада тому или иному потребителю можно считать известными. Рассмотрим пример транспортной задачи, исходные данные к которой представлены в табл. 8.3. В этой таблице, кроме объемов потребностей и величин запасов, приведены стоимости доставки единицы товара со склада i, i=1,2,3, потребителю j, j=1,2,3,4. Например, самая дешевая доставка - со склада 2 потребителям 1 и 3, а также со склада 3 потребителю 2. Однако на складе 2 имеется 80 единиц товара, а потребителям 1 и 3 требуется 50+70=120 единиц, поэтому к ним придется вести товар и с других складов. Обратите внимание, что в табл. 8.3 запасы на складах равны суммарным потребностям. Для примера с доставкой песка кирпичным заводам это вполне естественное ограничение - при невыполнении такого ограничения либо порты будут засыпаны горами песка, либо кирпичные заводы не выполнят заказы. Таблица 8.3 Исходные данные к транспортной задаче
Надо спланировать перевозки, т.е. выбрать объемы Xij поставок товара со склада i потребителю j, где i=1,2,3; j=1,2,3,4. Таким образом, всего в задаче имеется 12 переменных. Они удовлетворяют двум группам ограничений. Во-первых, заданы запасы на складах: X11 + X12 + X13 + X14 = 60, X21 + X22 + X23 + X24 = 80, X31 + X32 + X33 + X34 = 60, Во-вторых, известны потребности клиентов: X11 + X21 + X31 = 50, X12 + X22 + X32 = 40, X13 + X23 + X33 = 70, X14 + X24 + X34 = 40, Итак, всего 7 ограничений типа равенств. Кроме того, все переменные неотрицательны - еще 12 ограничений. Целевая функция - издержки по перевозке, которые необходимо минимизировать: 2X11 + 5X12 + 4X13 + 5X14 + X21 + 2X22 + X23 + 4X24 + 3X31 + X32 + 5X33 + 2X34min. Кроме обсуждаемой, рассматриваются также различные иные варианты транспортной задачи. Например, если доставка производится вагонами, то объемы поставок должны быть кратны вместимости вагона. Количество переменных и ограничений в транспортной задаче таково, что для ее решения не обойтись без компьютера и соответствующего программного продукта. Задача о выборе оборудования. На приобретение оборудования для нового участка цеха выделено 20000 долларов США. При этом можно занять площадь не более 38 м2. Имеется возможность приобрести станки типа А и станки типа Б. При этом станки типа А стоят 5000 долларов США, занимают площадь 8 м2 (включая необходимые технологические проходы) и имеют производительность 7 тыс. единиц продукции за смену. Станки типа Б стоят 2000 долларов США, занимают площадь 4 м2 и имеют производительность 3 тыс. единиц продукции за смену. Необходимо рассчитать оптимальный вариант приобретения оборудования, обеспечивающий при заданных ограничениях максимум общей производительности участка. Пусть Х - количество станков типа А, а Y - количество станков типа Б, входящих в комплект оборудования. Требуется выбрать комплект оборудования так, чтобы максимизировать производительность С участка (в тыс. единиц за смену): C=7X+3Ymax. При этом должны быть выполнены следующие ограничения: по стоимости (в тыс. долларов США): 5X+2Y≤20, по занимаемой площади (в м2 ): 8X+4Y≤38, а также вновь появляющиеся специфические ограничения по целочисленности, а именно, X ≥ 0, Y ≥ 0, X и Y - целые числа. Сформулированная математическая задача отличается от задачи линейного программирования только последним условием целочисленности. Однако наличие этого условия позволяет (в данном конкретном случае) легко решить задачу перебором. Действительно, как ограничение по стоимости, так и ограничение по площади дают, что X ≤ 4. Значит, Х может принимать лишь одно из 5 значений: 0, 1, 2, 3, 4. Если X=4, то из ограничения по стоимости следует, что Y=0, а потому C=7X=28. Если X=3, то из первого ограничения вытекает, что Y≤2, из второго Y≤3. Значит, максимальное С при условии выполнения ограничений достигается при Y=2, а именно C=21+6=27. Если X=2, то из первого ограничения следует, что Y≤5, из второго также Y≤5. Значит, максимальное С при условии выполнения ограничений достигается при Y=5, а именно C=14+15=29. Если X=1, то из первого ограничения имеем Y≤7, из второго также Y≤7. Значит, максимальное С при условии выполнения ограничений достигается при Y=7, а именно C=7+21=28. Если X=0, то из первого ограничения вытекает Y≤10, из второго Y≤9. Значит, максимальное С при условии выполнения ограничений достигается при Y=9, а именно, C=27. Все возможные случаи рассмотрены. Максимальная производительность C=29 (тысяч единиц продукции за смену) достигается при X=2, Y=5. Следовательно, надо покупать 2 станка типа А и 5 станков типа Б. Задача о ранце. Общий вес ранца заранее ограничен. Какие предметы положить в ранец, чтобы общая полезность отобранных предметов была максимальна? Вес каждого предмета известен. Есть много эквивалентных формулировок. Например, можно вместо ранца рассматривать космический аппарат - спутник Земли, а в качестве предметов - научные приборы. Тогда задача интерпретируется как отбор приборов для запуска на орбиту. Правда, при этом предполагается решенной предварительная задача - оценка сравнительной ценности исследований, для которых нужны те или иные приборы. С точки зрения экономики предприятия и организации производства более актуальна другая интерпретация задачи о ранце, в которой в качестве "предметов" рассматриваются заказы (или варианты выпуска партий тех или иных товаров), в качестве полезности - прибыль от выполнения того или иного заказа, а в качестве веса - себестоимость заказа. Перейдем к математической постановке. Предполагается, что имеется n предметов, и для каждого из них необходимо решить, класть его в ранец или не класть. Для описания решения вводятся булевы переменные Xk, k=1,2,…,n (т.е. переменные, принимающие два значения, а именно, 0 и 1). При этом Xk=1, если предмет размещают в ранце, и Xk=0, если нет, k=1,2,…,n. Для каждого предмета известны две константы: Ak - вес k-го предмета, и Ck - полезность k -го предмета, k=1,2,…,n. Максимально возможную вместимость ранца обозначим В. Оптимизационная задача имеет вид: C1X1+ C2X2+ C3X3+ … + CnXn max, A1X1+ A2X2+ A3X3+ … + AnXn ≤ B. В отличие от предыдущих задач, управляющие параметры Xk, k=1,2,…,n, принимают значения из множества, содержащего два элемента - 0 и 1. К целочисленному программированию относятся задачи размещения (производственных объектов), теории расписаний, календарного и оперативного планирования, назначения персонала и т.д. Укажем два распространенных метода решения задач целочисленного программирования. Задача коммивояжера. Требуется посетить все вершины графа и вернуться в исходную вершину, минимизировав затраты на проезд (или минимизировав время). Исходные данные здесь - это граф, дугам которого приписаны положительные числа - затраты на проезд или время, необходимое для продвижения из одной вершины в другую. В общем случае граф является ориентированным, и каждые две вершины соединяют две дуги - туда и обратно. Действительно, если пункт А расположен на горе, а пункт Б - в низине, то время на проезд из А в Б, очевидно, меньше времени на обратный проезд из Б в А. Многие постановки экономического содержания сводятся к задаче коммивояжера. Например: составить наиболее выгодный маршрут обхода наладчика в цехе (контролера, охранника, милиционера), отвечающего за должное функционирование заданного множества объектов (каждый из этих объектов моделируется вершиной графа); составить наиболее выгодный маршрут доставки деталей рабочим цеха или хлеба с хлебозавода по заданному числу булочных и других торговых точек (парковка у хлебозавода). Задача о кратчайшем пути. Как кратчайшим путем попасть из одной вершины графа в другую? В терминах производственного менеджмента: как кратчайшим путем (и, следовательно, с наименьшим расходом топлива и времени, наиболее дешево) попасть из пункта А в пункт Б? Для решения этой задачи каждой дуге ориентированного графа должно быть сопоставлено число - время движения по этой дуге от начальной вершины до конечной. Рассмотрим пример (рис. 8.7). 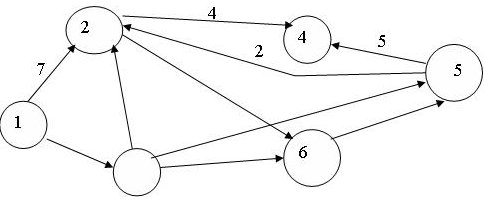 Рис. 8.7. Исходные данные к задаче о кратчайшем пути Ситуацию можно описать не только ориентированным графом с весами, приписанными дугам, но и таблицей (табл. 8.4). В этой таблице двум вершинам - началу пути и концу пути - ставится в соответствие время в пути. В табл. 8.4 рассматриваются пути без промежуточных остановок. Более сложные маршруты составляются из элементарных отрезков, перечисленных в табл. 8.4. Таблица 8.4 Исходные данные к задаче о кратчайшем пути
Спрашивается в задаче: как кратчайшим путем попасть из вершины 1 в вершину 4? Решение. Введем обозначение: С(Т) - длина кратчайшего пути из вершины 1 в вершину Т. (Поскольку любой путь, который надо рассмотреть, состоит из дуг, а дуг конечное число, и каждая входит не более одного раза, то претендентов на кратчайший путь конечное число, и минимум из конечного числа элементов всегда достигается.) Рассматриваемая задача состоит в вычислении С(4) и указании пути, на котором этот минимум достигается. Для исходных данных, представленных на pис. 8.7 и в табл. 8.4, в вершину 3 входит только одна стрелка, как раз из вершины 1, и около этой стрелки стоит ее длина, равная 1, поэтому C(3)=1. Кроме того, очевидно, что C(1)=0. В вершину 4 можно попасть либо из вершины 2, пройдя путь, равный 4, либо из вершины 5, пройдя путь, равный 5. Поэтому справедливо соотношение: C(4)=min{C(2)+4;C(5)+5}. Таким образом, проведена реструктуризация (упрощение) задачи – нахождение C(4) сведено к нахождению C(2) и C(5). В вершину 5 можно попасть либо из вершины 3, пройдя путь, равный 2, либо из вершины 6, пройдя путь, равный 3. Поэтому справедливо соотношение: C(5)=min{C(3)+2;C(6)+3}. Мы знаем, что C(3)=1. Поэтому: C(5)=min{3;C(6)+3}. Поскольку очевидно, что C(6)- положительное число, то из последнего соотношения вытекает, что C(5)=3. В вершину 2 можно попасть либо из вершины 1, пройдя путь, равный 7, либо из вершины 3, пройдя путь, равный 5, либо из вершины 5, пройдя путь, равный 2. Поэтому справедливо соотношение: C(2)=min{C(1)+7;C(3)+5;C(5)+2}. Нам известно, что C(1)=0, C(3)=1, C(5)=3. Поэтому:C(2)=min{0)+7;1)+5;3+2}=5. Теперь мы можем найти C(4): C(4)=min{C(2)+4;C(5)+5} = min{5+4;3+5}=8. Таким образом, длина кратчайшего пути равна 8. Из последнего соотношения ясно, что в вершину 4 надо идти через вершину 5. Возвращаясь к вычислению С(5), видим, что в вершину 5 надо идти через вершину 3. А в вершину 3 можно попасть только из вершины 1. Итак, кратчайший путь таков: 1 3 5 4. Задача о кратчайшем пути для конкретных исходных данных (рис. 8.7 и табл. 8.4) полностью решена. Оптимизационные задачи на графах, возникающие при подготовке управленческих решений в производственном менеджменте, весьма многообразны. Рассмотрим в качестве примера еще одну задачу, связанную с перевозками. Задача о максимальном потоке. Как (т.е. по каким маршрутам) послать максимально возможное количество грузов из начального пункта в конечный пункт, если пропускная способность путей между пунктами ограничена? Для решения этой задачи каждой дуге ориентированного графа, соответствующего транспортной системе, должно быть сопоставлено число - пропускная способность этой дуги. Рассмотрим пример (рис. 8.8). 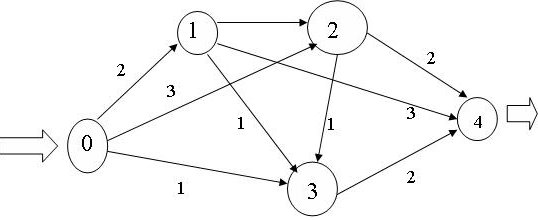 Рис. 8.8. Исходные данные к задаче о максимальном потоке Исходные данные о транспортной системе, например, внутризаводской, приведенные на рис. 8.8, можно также задать таблицей (табл. 8.5). Таблица 8.5 Исходные данные к задаче о максимальном потоке
Решение задачи о максимальном потоке может быть получено из следующих соображений. Очевидно, максимальная пропускная способность транспортной системы не превышает 6, поскольку не более 6 единиц грузов можно направить из начального пункта 0, а именно, 2 единицы в пункт 1, 3 единицы в пункт 2 и 1 единицу в пункт 3. Далее надо добиться, чтобы все 6 вышедших из пункта 0 единиц груза достигли конечного пункта 4. Очевидно, 2 единицы груза, пришедшие в пункт 1, можно непосредственно направить в пункт 4. Пришедшие в пункт 2 грузы придется разделить: 2 единицы сразу направить в пункт 4, а 1 единицу - в промежуточный пункт 3 (из-за ограниченной пропускной способности участка между пунктами 2 и 4). В пункт 3 доставлены такие грузы: 1 единица из пункта 0 и 1 единица из пункта 2. Их направляем в пункт 4. Итак, максимальная пропускная способность рассматриваемой транспортной системы - 6 единиц груза. При этом не используются внутренние участки (ветки) между пунктами 1 и 2, а также между пунктами 1 и 3. Не догружена ветка между пунктами 1 и 4 - по ней направлены 2 единицы груза при пропускной способности в 3 единицы. Решение можно представить в виде таблицы (табл. 8.6). Таблица 8.6 Решение задачи о максимальном потоке
Задача линейного программирования при максимизации потока. Дадим формулировку задачи о максимальном потоке в терминах линейного программирования. Пусть ХKM - объем перевозок из пункта К в пункт М. Согласно рис. 8.8 K=0,1,2,3, М=1,2,3,4, причем перевозки возможны лишь в пункт с большим номером. Значит, всего имеется 9 переменных XKM, а именно, X01,X02,X03,X12,X13,X14,X23,X24,X34. Задача линейного программирования, нацеленная на максимизацию потока, имеет вид: F max, X01 + X02 + X03 = F(0) -X01+X12+X13+X14=0(1) -X02+X12+X23+X24=0(2) -X03+X13+X23+X34=0(3) -X14+X24+X34=-F(4) X01≤2 X02≤3 X03≤1 X12≤4 X13≤1 X14≤3 X23≤1 X24≤2 X34≤2 ХKM≥0, K, M=0,1,2,3,4 F≥0 Здесь F - целевая функция, условие (0) описывает вхождение грузов в транспортную систему. Условия (1) - (3) задают балансовые соотношения для узлов 1- 3 системы. Другими словами, для каждого из внутренних узлов входящий поток грузов равен выходящему потоку, грузы не скапливаются внутри системы и не "рождаются" в ней. Условие (4) - это условие "выхода" грузов из системы. Вместе с условием (0) оно составляет балансовое соотношение для системы в целом ("вход" равен "выходу"). Следующие девять неравенств задают ограничения на пропускную способность отдельных "веток" транспортной системы. Затем в системе ограничений задачи линейного программирования указана неотрицательность объемов перевозок и целевой функции. Ясно, что последнее неравенство вытекает из вида целевой функции (соотношения (0) или (4)) и неотрицательности объемов перевозок. Однако последнее неравенство несет некоторую общую информацию - через систему может быть пропущен либо положительный объем грузов, либо нулевой (например, если внутри системы происходит движение по кругу), но не отрицательный (он не имеет экономического смысла, но формальная математическая модель об этом "не знает"). |
