Лекция. Лекция 07.09.2022 Системы счислени. Лекция (07. 09. 2022) Системы счисления. Методы перевода из одной системы счисления в другую
 Скачать 278.51 Kb. Скачать 278.51 Kb.
|
|
Лекция (07.09.2022) Системы счисления. Методы перевода из одной системы счисления в другую Основные понятия и определения Система счисления – совокупность символов и правил, позволяющих сформулировать и расшифровать любое число. Число – совокупность цифр, знаков и разделителя, позволяющая описать любое количество (вес). Минимально число может быть представлено только одной цифрой. В этом случае оно будет положительным и целым. Цифра – единичный символ алфавита системы счисления, используемый для обозначения фиксированного количества (веса). Знак – символ «+» или «-», определяющий явно положительность или отрицательность числа. Отсутствие знака подразумевает его положительность, т.е. положительность числа по умолчанию. Разделитель – символ «,» или «.», характеризующий форму представления количества, как целую (целочисленную) или дробную. Рассмотренные компоненты числа представим как основные и дополнительные. Основные символы – цифры, дополнительные – знаки и разделитель. Целое число – совокупность цифр без разделителя. Дробное число – совокупность цифр с разделителем. Позиционной называется система счисления, в которой значения каждой цифры числа зависит от месторасположения в ряду других, составляющих его. Основание системы счисления (q) – величина, определяющая конкретную систему счисления по отношению к любой другой. Основание определяет: количество цифр в алфавите; разность значений двух смежных разрядов. Представление чисел в позиционных системах может выполнятся в двух вариантах: компактном; развернутом. Использование основания позволяет получить полную развернутую запись любого числа в виде полинома со структурой: 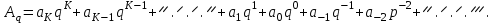 , ,где ai – цифра алфавита конкретной системы счисления; q – основание системы счисления; Двоичная система счисления. Используется две цифры: 0 и 1. В двоичной системе любое число может быть представлено в виде: 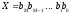 . . , ,где  либо 0, либо 1. либо 0, либо 1.Эта запись соответствует сумме степеней числа 2, взятых с указанными коэффициентами: 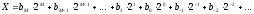 Восьмеричная система счисления. Используется восемь цифр: 0, 1, 2, 3, 4, 5, 6, 7. Употребляется в ЭВМ как вспомогательная для записи информации в сокращенном виде. Для представления одной цифры восьмеричной системы используется три двоичных разряда (триада) (Таб. 1). Шестнадцатеричная система счисления. Для изображения чисел употребляются 16 цифр. Первые десять цифр этой системы обозначаются цифрами от 0 до 9, а старшие шесть цифр – латинскими буквами: 10–A, 11–B, 12–C, 13–D, 14–E, 15–F. Шестнадцатеричная система используется для записи информации в сокращенном виде. Для представления одной цифры шестнадцатеричной системы счисления используется четыре двоичных разряда (тетрада). Таблица 1
Перевод чисел из одной системы счисления в другую Перевод чисел в десятичную систему осуществляется путем составления степенного ряда с основанием той системы, из которой число переводится. Затем подсчитывается значение суммы. Пример. а) Перевести 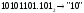 с.с. с.с. 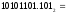 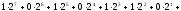 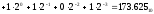 б) Перевести 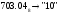 с.с. с.с.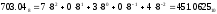 в) Перевести 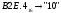 с.с. с.с.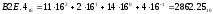 . .Перевод целых десятичных чисел в восьмеричную, шестнадцатеричную и двоичную системы осуществляется последовательным делением десятичного числа на основание той системы, в которую оно переводится, до тех пор, пока не получится частное меньшее этого основания. Число в новой системе записывается в виде остатков деления, начиная с последнего. Пример. а) Перевести 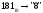 с.с. с.с.
Результат 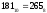 . .б) Перевести 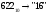 с.с. с.с.
 Результат 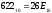 . .Перевод правильных дробей из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную системы счисления. Для перевода правильной десятичной дроби в другую систему эту дробь надо последовательно умножать на основание той системы, в которую она переводится. При этом умножаются только дробные части. Дробь в новой системе записывается в виде целых частей произведений, начиная с первого. Пример. Перевести 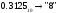 с.с. с.с.
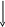 Результат 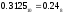 . .Замечание. Конечной десятичной дроби в другой системе счисления может соответствовать бесконечная (иногда периодическая) дробь. В этом случае количество знаков в представлении дроби в новой системе берется в зависимости от требуемой точности. Пример. Перевести 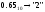 с.с. Точность 6 знаков. с.с. Точность 6 знаков.
 Результат 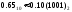 . .Для перевода неправильной десятичной дроби в систему счисления с недесятичным основанием необходимо отдельно перевести целую часть и отдельно дробную. Пример. Перевести 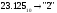 с.с. с.с.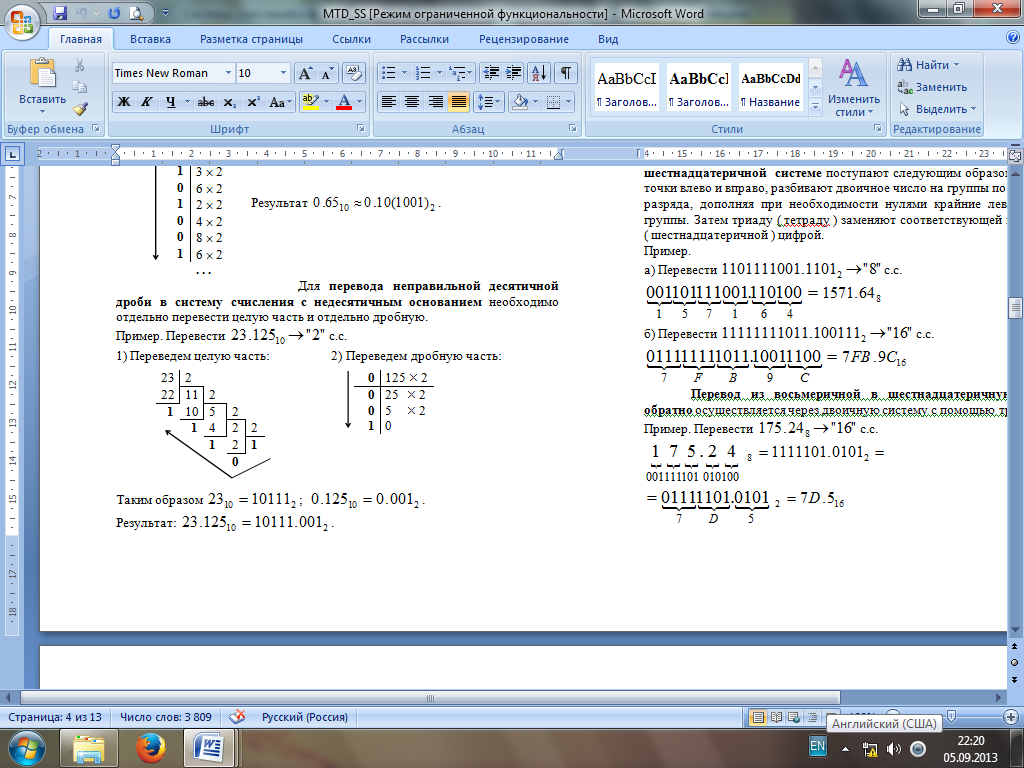 Таким образом 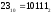 ; ; 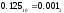 . .Результат: 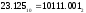 . .Для перевода восьмеричного или шестнадцатеричного числа в двоичную форму достаточно заменить каждую цифру этого числа соответствующим трехразрядным двоичным числом (триадой) (Таб. 1) или четырехразрядным двоичным числом (тетрадой) (Таб. 1), при этом отбрасывают ненужные нули в старших и младших разрядах. Пример. а) 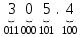  = = 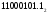 ; ; б) 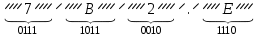  = = 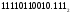 . .Для перехода от двоичной к восьмеричной или шестнадцатеричной системе поступают следующим образом: двигаясь от точки влево и вправо, разбивают двоичное число на группы по три ( четыре ) разряда, дополняя при необходимости нулями крайние левую и правую группы. Затем триаду ( тетраду ) заменяют соответствующей восьмеричной ( шестнадцатеричной ) цифрой. Пример. а) Перевести 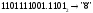 с.с. с.с.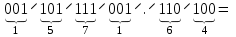 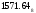 б) Перевести 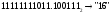 с.с. с.с.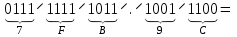 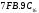 Перевод из восьмеричной в шестнадцатеричную систему и обратно осуществляется через двоичную систему с помощью триад и тетрад. Пример. Перевести 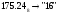 с.с. с.с.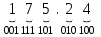  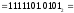  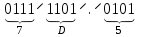  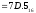 Результат: 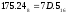 . .Контрольные вопросы Что такое система счисления? Основание системы счисления? Что такое позиционные и непозиционные системы счисления? Что такое двоичная, восьмеричная, шестнадцатеричная системы счисления? Основные методы перевода их одной системы счисления в другую? | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||




 128
128 14
14 8
8