Лекции по ПСУ, ч.2. Лекция 1 Критериальный язык описания задачи выбора

• Название: Лекция 1 Критериальный язык описания задачи выбора
• Дата: 14.03.2023
• Размер: 4.27 Mb.
• Имя файла: Лекции по ПСУ, ч.2.doc
• Тип: Лекция; #988620
• страница: 1 из 5

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное бюджетное государственное образовательное учреждение высшего профессионального образования

«Московский государственный университет» (ФБГОУ ВПО МГИУ)

Кириличев Б.В.
Проектирование систем управления

ч.2

Москва, 2012

Лекция №1

1. Критериальный язык описания задачи выбора
1.1. Многокритериальная оптимизация
В процессе проектирования очень часто приходится сталкиваться с необходимостью поиска такого варианта (альтернативы), который удовлетворял бы сразу нескольким, порой противоречивым, критериям оптимальности. Например, таким как: точность, быстродействие, надежность, вес, стоимость и т.д.

Стремление учесть одновременно несколько критериев и приводит к задаче многокритериальной, или векторной оптимизации.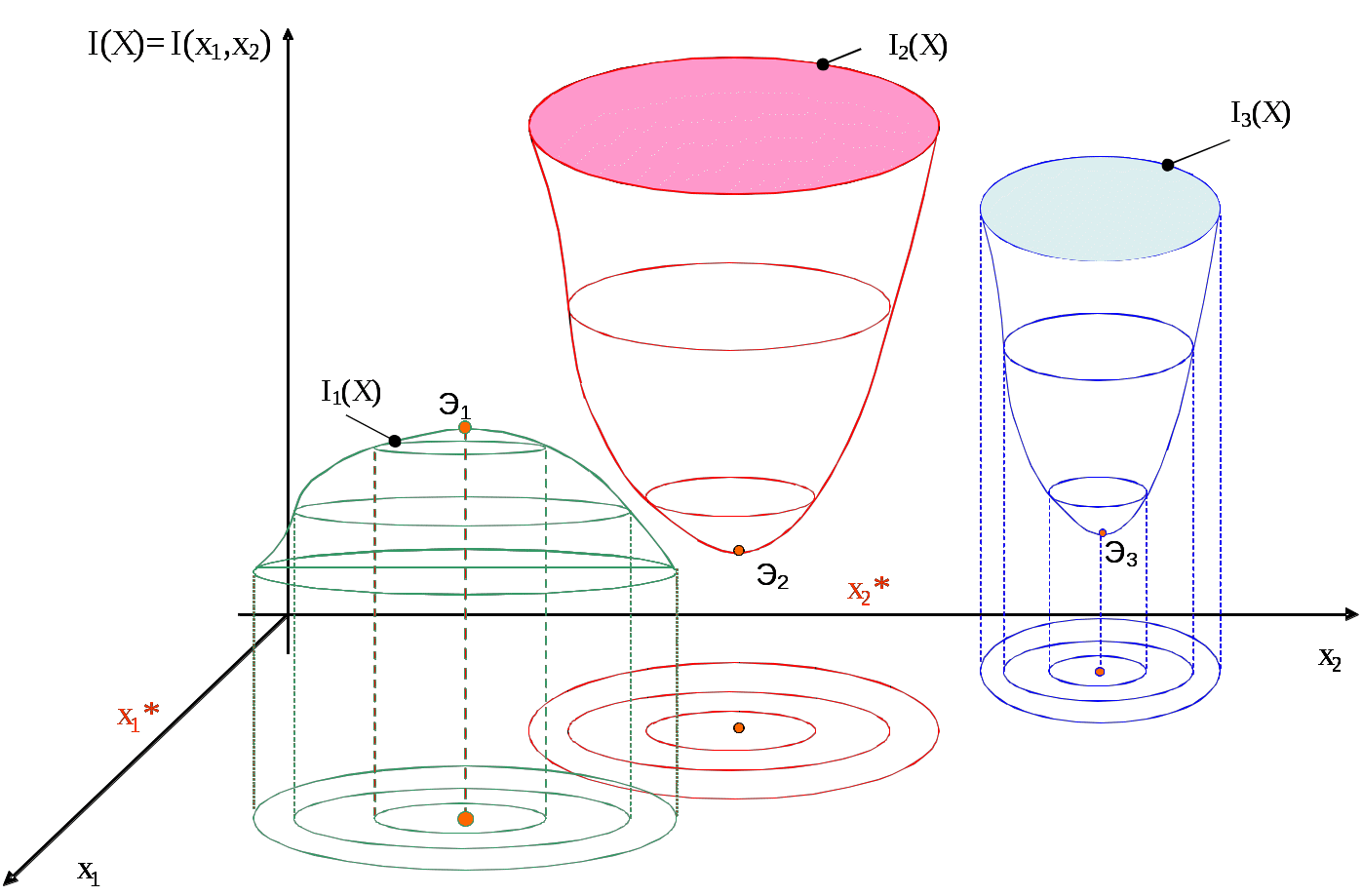



Рис. 1. К понятию многокритериальной оптимизации
На рис. 1 показана ситуация, когда экстремумы трех различных целевых функций (соответствующих различным критериям оптимальности) не совпадают, а находятся в различных точках пространства X внутренних (варьируемых, управляемых) параметров. Очевидно, что в этом случае выбор компромиссных значений проектных параметров представляет собой непростую задачу.
Существует несколько языков описания проблемы выбора; наиболее употребимы следующие: критериальный язык выбора, язык бинарных отношений, язык функций выбора.

Введем общие понятия для всех задач выбора:

Принятие решения (выбор) – действие над множеством альтернатив, в результате которого, получается подмножество выбранных альтернатив.

Сужение множества альтернатив возможно, если существует способ сравнения альтернатив между собой и определения наиболее предпочтительных. Каждый такой способ называется критерием предпочтения.

Однако прежде необходимо выполнить ряд этапов:

1. Порождение множества альтернатив, из которых предстоит сделать выбор.

2. Определение целей, для достижения которых осуществляется выбор.

Стоит помнить также, что способ порождения альтернатив определяет выбор.
1.2. Множественность задач выбора
Даже в упрощенной постановке, проблема выбора нетривиальна и имеет расхождения в математических постановках задач. Существует множество различных ситуаций выбора и все их можно классифицировать в зависимости от следующих факторов:

1. Свойства множества альтернатив. Это множество может быть конечным, счетным (каждому элементу соответствует некоторое число, номер) или континуальным (между двумя любыми элементами множества может располагаться бесконечное число других элементов множества).

2. Оценка альтернатив может осуществляться по одному или нескольким критериям. Критерии могут иметь как количественный, так и качественный характер.

3. Режим выбора может быть однократным или повторяющимся, допускающим обучение на опыте.

4. Последствия выбора могут быть известны (выбор в условиях определенности), либо может иметь вероятностный характер (известны вероятности возможных исходов, выбор в условиях риска). Выбор может иметь неоднозначный исход, не допускающий введения вероятностей возможных исходов (выбор в условиях неопределенности).

5. Ответственность за выбор может быть односторонней и в частном случае индивидуальной, либо многосторонней. Тогда в первом случае, выбор называют индивидуальным, а во втором групповым.

6. Степень согласованности цели. В случае многостороннего выбора может различаться от полного совпадения (консенсуса), частичного совпадения (компромиссный, или коалиционный выбор), до полного несовпадения целей (выбор в условиях конфликта).

Различные сочетания выше перечисленных вариантов приводят к многообразным задачам выбора, которые изучены в разной степени.

1.3. Классификация критериальных задач выбора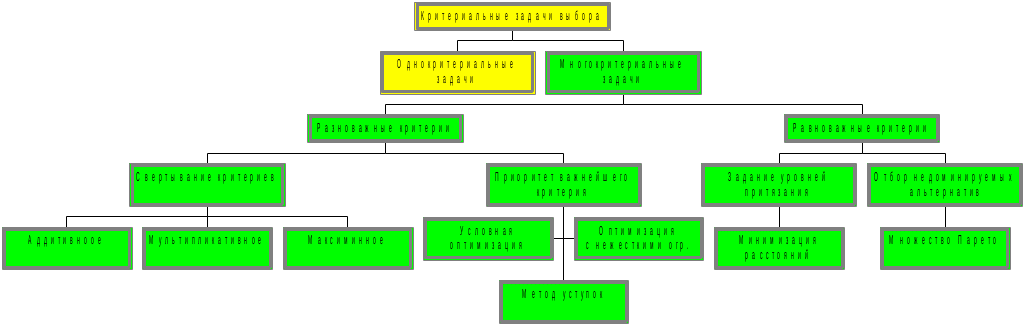



Рис. 2. Классификация задач принятия решений, описываемых на критериальном языке
1.4. Сведение многокритериальной задачи к однокритериальной
Это можно осуществить с помощью введения суперкритерия – скалярной функции векторного аргумента: , так что задача сведется к максимизации этого суперкритерия:



Суперкритерий позволяет упорядочить альтернативы по величине I_sup, выделив, таким образом, наилучшую (в смысле этого суперкритерия) альтернативу. Конкретный вид функции I_supопределяется тем, как мы представляем себе вклад каждого частного критерия в суперкритерий. Чаще всего используют аддитивные функции вида:




(1)
или мультипликативные функции вида:




(2)

Коэффициенты α_iиβ_iотражают относительный вклад частных критериев в суперкритерий. Коэффициенты γ_iобеспечивают безразмерность величин I_i / γ_i , что необходимо, например, когда частные критерии имеют разную размерность, препятствующую выполнению арифметических операций над ними (бессмысленно, например, складывать килограммы с рублями!). Кроме того, при необходимости указанные коэффициенты обеспечивают нормирование (например, в приведенном выражении (2) должно выполняться условие

( 3)
Достоинства и недостатки свертки (скаляризации) критериев
Преимущество объединения нескольких критериев (векторного критерия) в один скалярный суперкритерий состоит в возможности однократного использования процедуры поиска экстремума этого критерия одним из известных методов и одновременного удовлетворения при этом требованиям всех различных частных критериев, входящих в суперкритерий.

Недостатком является то, что суперкритерий выполняет роль функции, упорядочивающей альтернативы в многомерном пространстве критериев. Однако известно, что упорядочивание точек (альтернатив) в многомерном пространстве в принципе не может быть однозначным и полностью определяется видом упорядочивающей функции. Поэтому даже небольшое изменение суперкритерия (например, его коэффициентов α_iи γ_i) может привести к тому, что оптимальная в новом смысле альтернатива будет сильно отличаться от прежней.

На рисунке 3 видно, как изменяется выбор наилучшей альтернативы при смене коэффициентов в линейной упорядочивающей функции (1):



что отражается в изменении наклона соответствующей прямой:



Линейные комбинации частных критериев придают упорядочению смысл: «чем дальше от нуля в заданном направлении, тем лучше».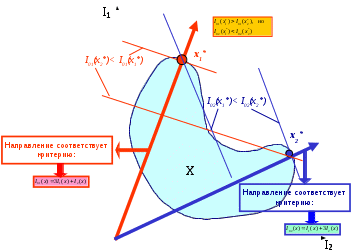


Рис. 3. Изменение выбора наилучшей альтернативы при смене коэффициентов в линейной упорядочивающей функции
Другой вариант поиска альтернативы, наиболее удаленной от нуля в заданном направлении.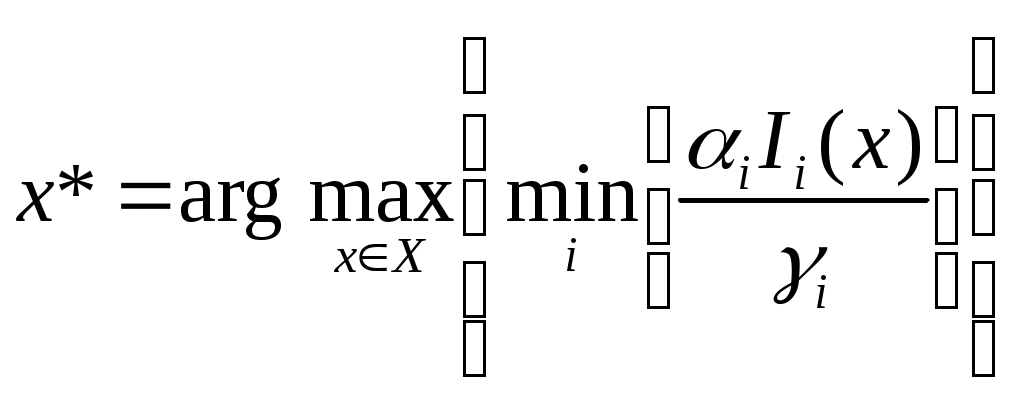



(4)



Это означает поиск вокруг направления

методом «подтягивания самого отстающего».
1.5. Условная максимизация
Недостатки свертывания нескольких критериев в суперкритерий вынуждают применять другие подходы к решению многокритериальных задач выбора.

Например, можно использовать тот факт, что частные критерии обычно неравнозначны между собой, т.е. одни из них более важны, чем другие.

В предельном случае выделяют один основной, или главный критерий, а остальные рассматривают как дополнительные, второстепенные, сопутствующие.

В результате можно сформулировать задачу выбора как задачу нахождения условного экстремума основного критерия:

(5)
при условии, что дополнительные критерии остаются на заданных им уровнях С_i (рис. 4).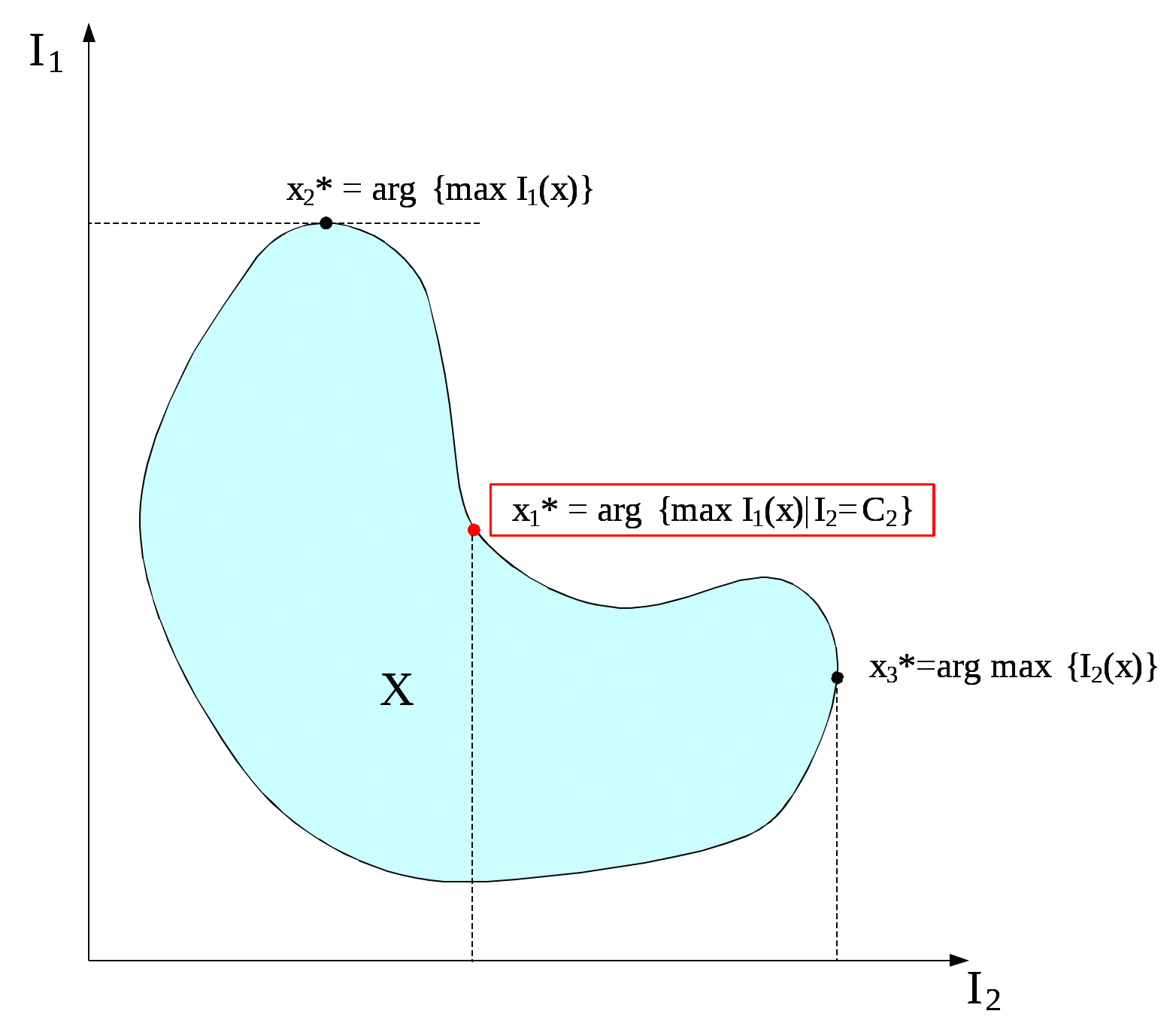

Рис. 4. К решению задачи выбора методом условной максимизации
В некоторых задачах бывает нужно задавать ограничения на дополнительные критерии не жестко, как в предыдущем случае.

Например, если сопутствующий критерий характеризует стоимость затрат, то вместо жесткой фиксации затрат разумнее задавать их верхний уровень, а значит, формулировать задачу с ограничениями типа неравенств:




(6)
Такой метод решения иллюстрирует рис. 5. Оказывается, что столь незначительное на первый взгляд изменение постановки задачи (по сравнению с жесткими ограничениями) требует принципиально иных методов ее решения.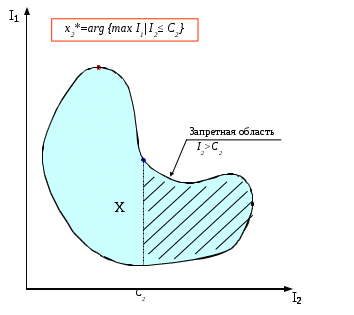



Рис. 5. К решению задачи выбора методом условной максимизации с нежесткими ограничениями
1.6. Метод уступок
В том случае, когда различия между основным и дополнительными критериями не так велико, как в методе условной максимизации, можно упорядочить частные критерии в порядке убывания их важности.

Затем берется первый из них (самый важный) и находится наилучшая по этому критерию альтернатива (на рисунке 6 это x₃*, если самый важный критерий – I₁, или x₄*, если самый важный критерий – I₂).

Далее определяется «уступка» ΔI_i, т.е. величина, на которую мы согласны уменьшить достигнутое значение самого важного критерия, чтобы за счет уступки попытаться увеличить, насколько возможно, значение следующего по важности критерия, и т.д.

На рис. 6 полученные таким образом альтернативы изображены точками x₅* и x₆*).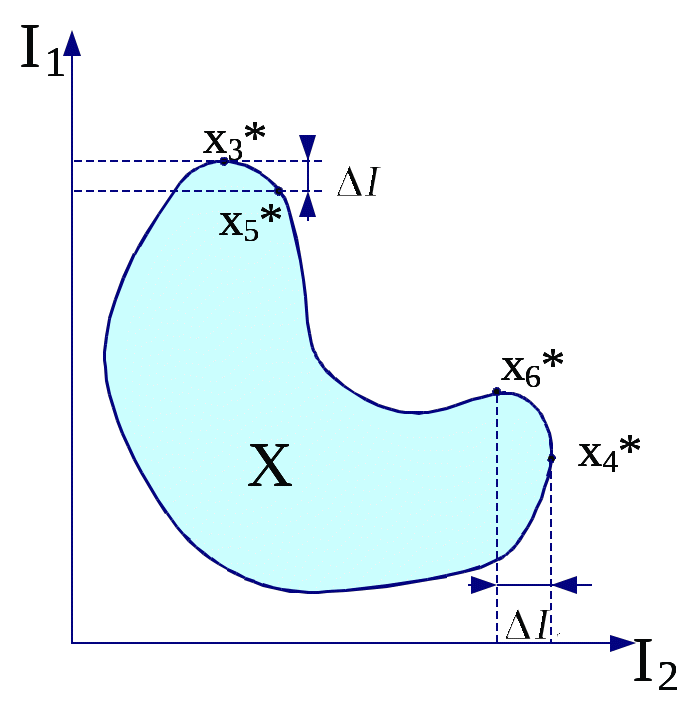


Рис. 6. К методу уступок

1.7. Поиск альтернативы с заданными свойствами
Этот метод многокритериального выбора относится к тому случаю, когда заранее могут быть указаны значения частных критериев (или их границы).

Задача состоит в том, чтобы найти альтернативу, удовлетворяющую этим требованиям. Если же такая альтернатива во множестве X отсутствует, то найти в этом множестве альтернативу, наиболее близкую к поставленным целям.

При этом удобным является возможность заранее задавать желательные значения критериев Î_i как точно, так и в виде верхних или нижних границ.

Назначаемые величины называют уровнями притязаний, а точку их пересечения в k-мерном пространстве критериев – идеальной точкой, целью.

На рисунке 7 это точка x₁*; она соответствует недостижимой цели, т.к. не принадлежит множеству X. Достижимой цели соответствует точка x₂*.

После того, как цель задана, идея оптимизации состоит в том, чтобы, начав с любой альтернативы, приближаться к цели x* по некоторой траектории в пространстве X. Это достигается введением числовой меры близости между очередной альтернативой и целью x*, т.е. между векторами I(x)=[I₁(x),I₂(x),…,I_k(x)] и Î(x)=[Î₁(x), Î₂(x),…, Î_k(x)].

Количественно эту меру близости можно описать по-разному. Например, с помощью расстояния: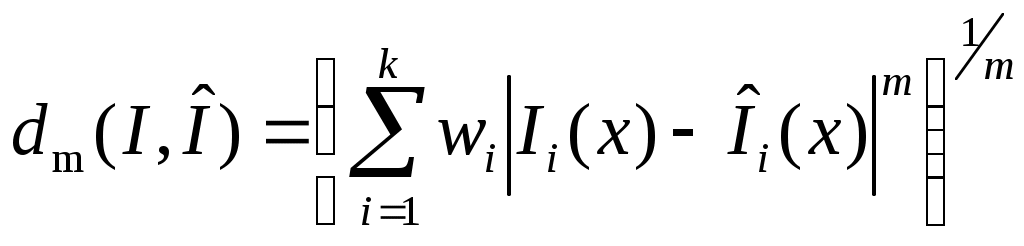




(7)



Рис. 7. К поиску альтернативы с заданными свойствами
Либо с помощью расстояния:




(8)
Здесь считается, что I_i ≥ Î_i , α_i – коэффициенты, приводящие слагаемые к одинаковой размерности и одновременно учитывающие разноважность критериев, α_k+1 – коэффициент, который выражает наше отношение к тому, что важнее – уменьшать близость к цели любого из частных критериев или суммарную близость всех критериев к целевым значениям.

1.8. Нахождение множества Парето¹
Метод состоит в отказе от выделения единственной «наилучшей» альтернативы и соглашении о том, что предпочтение одной альтернативе перед другой можно отдавать, только если первая по всем критериям лучше второй. Если же предпочтение хотя бы по одному критерию расходится с предпочтением по другому, то такие альтернативы признаются несравнимыми.

В результате попарного сравнения альтернатив все худшие по всем критериям альтернативы отбрасываются, а все оставшиеся несравнимые между собой (недоминируемые) принимаются. Если все максимально достижимые значения частных критериев не относятся к одной и той же альтернативе, то принятые альтернативы образуют множество Парето и выбор на этом заканчивается.



Рис. 8. К нахождению множества Парето
Множество состояний системы, оптимальных по Парето, называют «множеством Парето», «множеством альтернатив, оптимальных в смысле Парето», либо «множеством парето-оптимальных альтернатив».

При необходимости выбора единственной альтернативы следует привлекать дополнительные меры: вводить новые, добавочные критерии и ограничения, либо бросать жребий, либо привлекать экспертов.
2. Групповой выбор
На множестве альтернатив X задано n различных индивидуальных предпочтений (например, бинарных отношений) R₁, R₂, …, R_n. Необходимо выработать некоторое новое отношение R, которое согласует индивидуальные выборы, выражает некое «общее мнение» и принимается за групповой выбор.

Очевидно, что R=F(R₁, R₂, …, R_n). Различным принципам согласования, т.е. Различным вариантам Группового голосования будут соответствовать различные функции F.
2.1. Различные правила голосования

1. 
   Правило большинства: принятой всеми считается альтернатива, получившая наибольшее число голосов.
   

Замечания:

а) оно лишь обобщает индивидуальные предпочтения, но его результат не является критерием истины;

б) возможны «тупики», например, при разделении голосов поровну (в случае четного числа голосующих).

Различают простое большинство (51%), подавляющее (около 75%), абсолютное (близкое к 100%) и, наконец, консенсус (единогласие) – ровно 100%.
2.2. Парадокс многоступенчатого голосования при наличии коалиции



Рис. 9. К парадоксу многоступенчатого голосования при наличии коалиции

Лекция №2

3. Процедуры синтеза проектных решений
Принятие проектных решений охватывает широкий круг задач и процедур – от выбора вариантов в конечных и обозримых множествах до задач творческого характера, не имеющих формальных способов решения.




Рис. 10. Синтез проектных решений
Структурный синтез заключается в преобразовании описаний проектируемого объекта: исходное описание содержит информацию о требованиях к свойствам объекта, об условиях его функционирования, ограничениях на элементный состав и т. п., а результирующее описание должно содержать сведения о структуре, т. е. о составе элементов и способах их соединения и взаимодействия.
3.1. Математическая формулировка критериальной задачи принятия решений
Задачу принятия решений(ЗПР) в общем виде формулируют следующим образом:

ЗПР = < А, К, Мод, П >,

где А – множество альтернатив проектного решения;

К = (К1,К2, ..., Кm) – множество критериев (выходных параметров), по которым оценивается соответствие альтернативы поставленным целям;

Мод: А→ К – модель, позволяющая для каждой альтернативы рассчитать вектор критериев;

П – решающее правило для выбора наиболее подходящей альтернативы в многокритериальной ситуации.

Каждой альтернативе конкретного приложения можно поставить в соответствие значения упорядоченного множества (набора) атрибутов

Х = < х₁, х₂, ..., х_n>,

характеризующих ее свойства. При этом х_iможет быть величиной типа: real, integer, Boolean, string (в последнем случае величину называют предметной или лингвистической). Множество Х называют записью (в теории баз данных), фреймом (в искусственном интеллекте) или хромосомой (в генетических алгоритмах). Модель Мод называют структурно-критериальной, если среди x_i, имеются параметры, характеризующие структуру моделируемого объекта.
3.2. Основные проблемы ЗПР

1. 
   Компактное представление множества вариантов (альтернатив);
   
2. 
   Построение модели синтезируемого устройства, в том числе выбор степени абстрагирования для оценки значений критериев;
   
3. 
   Формулировка предпочтений в многокритериальных ситуациях (т. е. преобразование векторного критерия К в скалярную целевую функцию);
   
4. 
   Установление порядка (предпочтений) между альтернативами при отсутствии количественной оценки целевой функции (что обычно является следствием неколичественного характера всех или части критериев);
   
5. 
   Выбор метода поиска оптимального варианта (сокращение перебора вариантов).
   

3.3. Представление множества альтернатив
Простейший способ задания множества А – явное перечисление всех альтернатив. Семантика и форма описания альтернатив существенно зависят от приложения. Для представления таких описаний в памяти ЭВМ и доступа к ним используют информационно-поисковые системы (ИПС). Каждой альтернативе в ИПС соответствует поисковый образ, состоящий из значений атрибутов х_iи ключевых слов вербальных характеристик.

Явное перечисление альтернатив при представлении множества альтернатив возможно лишь при малой мощности А. Поэтому в большинстве случаев используют неявное описание А в виде способа (алгоритма или набора правил P) синтеза проектных решений из ограниченного набора элементов Э. Поэтому здесь А = < Р, Э >, а типичный процесс синтеза проектных решений состоит из следующих этапов:

1. 
   формирование альтернативы А, (это может быть выбор из базы данных ИПС по сформированному поисковому предписанию или генерация из Э в соответствии с правилами Р);
   

2) оценка альтернативы по результатам моделирования с помощью модели Мод;

3) принятие решения (выполняется ЛПР – лицом, принимающим решение, или автоматически) относительно перехода к следующей альтернативе или прекращения поиска.
Для описания множеств Р и Э используют следующие подходы:

1. 
   Морфологические таблицы и альтернативные И-ИЛИ-деревья.
   
2. 
   Представление знаний в интеллектуальных системах – фреймы, семантические сети, продукции.
   
3. 
   Генетические методы.
   
4. 
   Базы физических эффектов и эвристических приемов, применяемые при решении задач изобретательского характера.
   

3.4. Морфологические таблицы
Морфологическая таблица(М) представляет собой обобщенную структуру в виде множества функций, выполняемых компонентами синтезируемых объектов рассматриваемого класса, и подмножеств способов их реализации.

Каждой функции можно поставить в соответствие одну строку таблицы, каждому способу ее реализации – одну клетку в этой строке.

В морфологических таблицах элемент М_ijозначает j-й вариант реализации i-й функции в классе технических объектов, описываемом матрицей М.

Множество альтернатив можно представить в виде отношения М, называемого морфологической таблицей:

М=<Х,R>,

где Х – множество свойств (характеристик или функций), присущих объектам рассматриваемого типа; n — число этих свойств;

R = < R₁, ,R₂, ... , R_n >, R – множество значений (способов реализации) i –го свойства; мощность этого множества далее обозначена N_i.

При этом собственно множество альтернатив А представлено композицией множеств R_i , т. е. каждая альтернатива включает по одному элементу (значению) из каждой строки морфологической таблицы.

Общее число альтернатив k, представляемых морфологической таблицей, равно



Морфологические таблицы обычно считают средством неавтоматизированного синтеза, помогающим человеку просматривать компактно представленные альтернативы, преодолевать психологическую инерцию. Это связано с тем, что внимание ЛПР обращается на варианты, которые без морфологической таблицы оставались бы вне его поля зрения.

Таблица М не содержит сведений о способе синтеза. Однако на базе М возможно построение методов синтеза с элементами алгоритмизации. В таких методах вводится метризация морфологического пространства. Морфологическое пространство составляют возможные законченные структуры, принимается, что расстояние между структурами С₁ и С₂ есть число несовпадающих элементов (каждая клетка М есть один элемент). Поэтому можно говорить об окрестностях решений. Далее исходят из предположения о компактности «хороших» решений, которое позволяет вместо полного перебора ограничиваться перебором в малой окрестности текущей точки поиска. Таким образом, гипотеза о «компактности» и метризация пространства решений фактически приводят к построению математической модели, к которой можно применить методы дискретной оптимизации, например локальные методы.
3.5. Альтернативные графы
Любую морфологическую таблицу можно представить в виде дерева (рис. 11).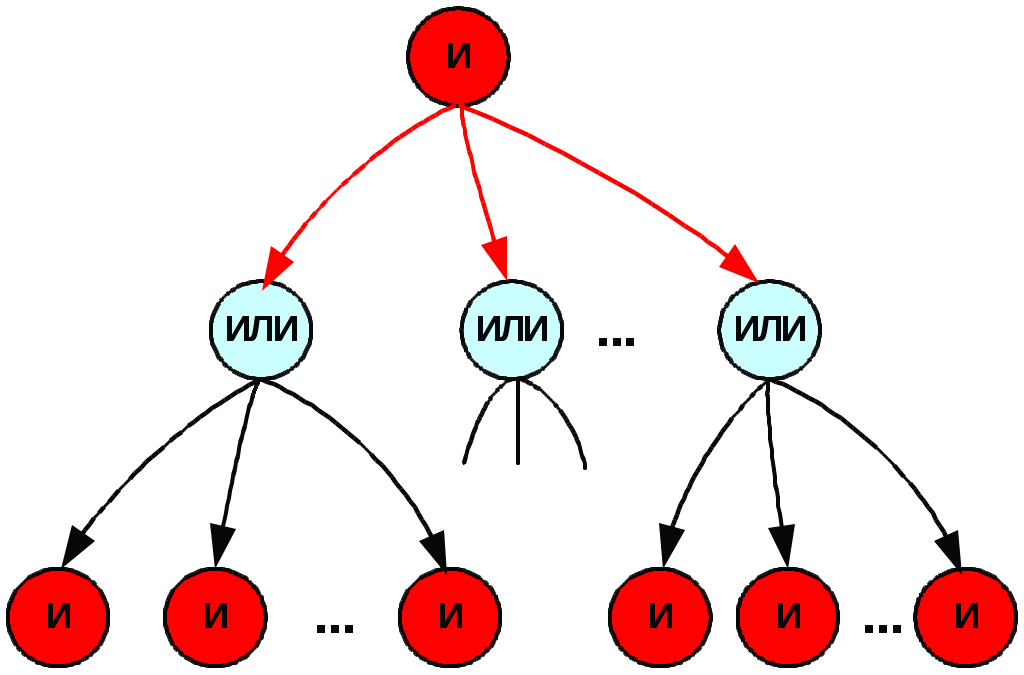



Рис. 11. И-ИЛИ-дерево

На рисунке функции представлены вершинами И – красные кружки, значения функций – вершинами ИЛИ – голубые кружки
Таблица представляет множество однотипных объектов, поскольку все они характеризуются одним и тем же множеством функций
3.6. Многоярусные альтернативные графы
Двухъярусный граф, в котором для разных типов объектов предусмотрены разные подмножества функций, показан на рис. 12.

И-ИЛИ-дерево можно представить как совокупность морфологических таблиц. Каждая И вершина дерева соответствует частной морфологической таблице, т. е. множеству функций, так, что i-я выходящая ветвь отображает i-ю функцию. Каждая ИЛИ вершина, инцидентная i-й ветви, соответствует множеству вариантов реализации i-й функции, при этом j-я исходящая из ИЛИ вершины ветвь отображает j-й вариант реализации.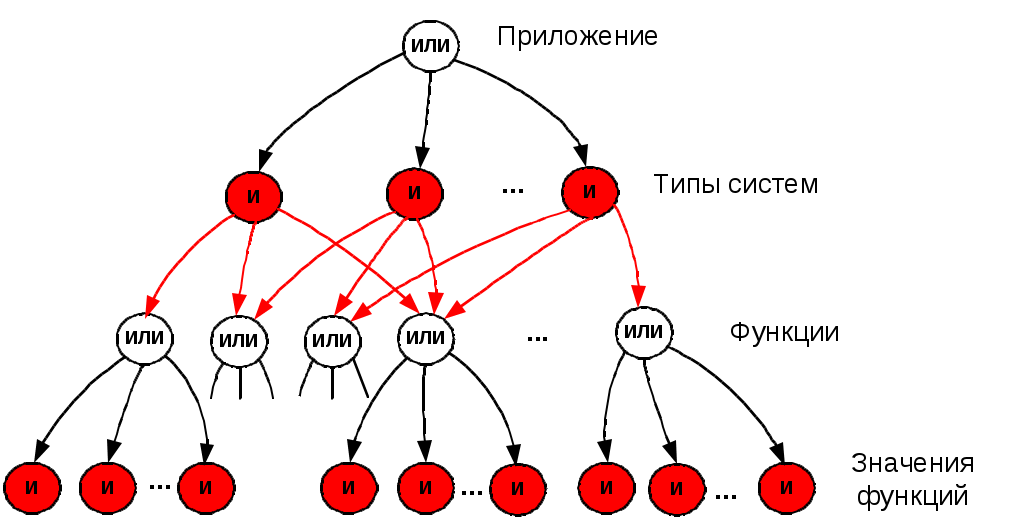



Рис. 12. Двухъярусный альтернативный граф
3.7. Алгоритмизация синтеза на базе И-ИЛИ-деревьев
Требует введения правил выбора альтернатив в каждой вершине ИЛИ. Эти правила чаще всего имеют эвристический характер, связаны с требованиями ТЗ, могут отражать запреты на сочетания определенных компонентов структур.

Трудности эффективного решения задачи существенно возрастают при

наличии ограничений, типичными среди которых являются ограничения

на совместимость способов реализации разных функций, т. е. ограничения

вида:

С_ij and С_pq= false,

где С_ij= true, если в оцениваемый вариант вошел элемент Э_ij, иначе С_ij = false.

Данное условие означает, что в допустимую структуру не могут входить одновременно элементы Э_ij и Э_pq. Совокупность подобных ограничений можно представить как систему логических уравнений с неизвестными С_ij. Тогда задачу синтеза можно решать эволюционными методами, если предварительно или одновременно с ней решать систему логических уравнений (задачу о выполнимости).
Лекция №3

4. 
   Язык функций выбора
   

Язык функций выбора (ЯФВ) описывает выбор как операцию над произвольным множеством альтернатив X, ставящую ему в соответствие некоторое его подмножество C(X): C(X)Í X .

ЯФВ применяется, когда предпочтение между двумя альтернативами зависит от остальных альтернатив.

ЯФВ применяется, когда предпочтения вообще лишены смысла: выбор «типичного», «среднего» или наоборот, «самого оригинального» – теряют смысл в случае двух альтернатив.

Основное преимущество ЯФВ – возможность рассмотрения более сложных правил выбора, чем при использовании других языков.
4.1. Число функций выбора на множестве n альтернатив
Число возможных ФВ очень велико Оно намного превышает число возможных графов предпочтения на множестве n альтернатив:


п оскольку число графов, отличающихся наличием или отсутствием хотя бы одной дуги, равно .

Если для выбора предлагаются k из n альтернатив, то число ФВ равно 2^k, т.к. каждая из альтернатив может либо входить в C(X_k), либо нет. А поскольку число возможных вариантов предъявления альтернатив равно C_n^k, то получается, что общее число ФВ равно

2. 
   Ограничения на функции выбора
   

Итак, при отсутствии каких-либо ограничений на функции выбора их количество чрезвычайно велико. Сократить это количество до приемлемых величин помогают ограничения в форме аксиом, которым должны удовлетворять функции выбора. Эти аксиомы логически понятны и соответствуют тем или иным условиям конкретных ситуаций выбора.

4.2.1. Аксиома наследования (Н)
В 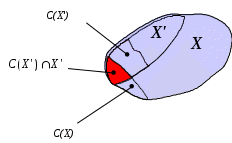выбор на подмножестве альтернатив X’ вошли все альтернативы их X’, которые входили в выбор на X и, возможно, еще и другие:



Рис. 13. К аксиоме наследования
4.2.2. Аксиома согласия (С)
В выбор из объединения множеств обязательно должны входить альтернативы, общие для выбора из всех множеств (и еще могут входить и некоторые другие):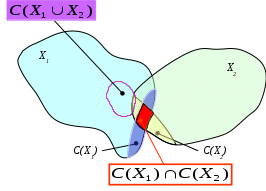





Рис. 14. К аксиоме согласия
4.2.3. Аксиома отбрасывания (О)
Если отбросить любую часть отвергнутых при выборе альтернатив, то выбор на оставшемся множестве не изменится. Другое название этой аксиомы – условие независимости от отвергнутых альтернатив.



Рис. 15. К аксиоме отбрасывания
4.2.4. Аксиома квазисумматорности (КС)
Эта аксиома отражает требования, накладываемые при многоступенчатых выборах, когда считается, что лучшая альтернатива может определяться как при выборе из лучших альтернатив отдельных непересекающихся классов, так и при выборе из всех альтернатив множества, объединяющего классы.

Другое название аксиомы – условие независимости от пути. Она также носит название аксиомы Плотта.

Функции выбора, удовлетворяющие этой аксиоме (КС) также называются квазисумматорными.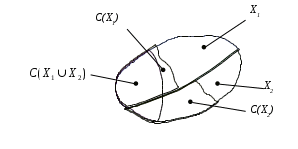





Рис. 16. К аксиоме Плотта
4.2.5. Аксиома предпочтения (П)
Эта аксиома отражает требование, чтобы при сужении множества альтернатив для выбора оставались только те альтернативы, которые входили в выбор раньше: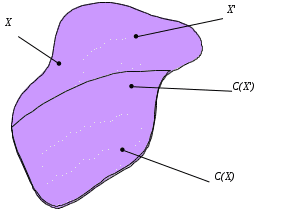





Рис. 17. К аксиоме предпочтения
4.2.6. Аксиома сумматорности (Сум)
Эта аксиома отражает требование, чтобы выбор лучшей альтернативы был эквивалентен как при выборе из лучших альтернатив отдельных непересекающихся классов, так и при выборе из всех альтернатив множества, объединяющего классы:


Эту аксиому можно считать усилением аксиомы Плотта (КС).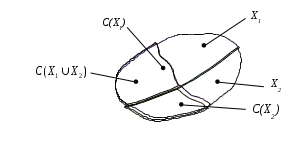

Рис. 18. К аксиоме сумматорности

4.2.7. Аксиома монотоности (М)
Эта аксиома отражает требование, чтобы при сужении множества альтернатив для выбора оставались только те альтернативы, которые входили в выбор раньше: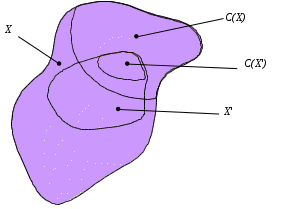





Рис. 19. К аксиоме монотонности


4.2.8. Аксиома мультипликаторности (МП)
Эта аксиома отражает требование, чтобы выбор из общих для множеств альтернатив был эквивалентен множеству альтернатив, общих для выборов, произведенных раньше из отдельных множеств.

Иначе говоря, выбор из пересечения эквивалентен пересечению выборов: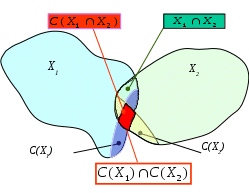





Рис. 20. К аксиоме мультипликаторности
4.2.9. Применение аксиом для формирования правил выбора
Итак, различие между классами правил выбора можно выразить через

различные ограничения (задаваемые аксиомами). Отдельные ограничения

дают известные правила выбора, другие определяют новые правила.

Так, например, совместное выполнение требований аксиом наследования Н, отбрасывания О и согласия С приводит к случаю выбора множества Парето.

Совместное выполнение требований аксиом наследования Н, и отбрасывания О приводит к случаю выбора, независимого от пути.

Совместное же выполнение требований аксиом наследования Н и согласия С приводит к случаю выбора, описываемому в языке бинарных отношений.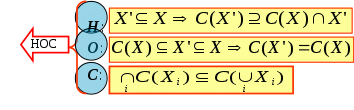



Рис. 21. Выбор Парето-оптимальной альтернативы как результат одновременного выполнения требований аксиом наследования, отбрасывания и согласия.

Можно наоборот, изучив ограничения какого-либо реального правила выбора, искать свойства класса ФВ, удовлетворяющие этим ограничениям.
Лекция №4

4. 
   Язык бинарных отношений
   

Язык бинарных отношений описывает ситуацию выбора из двух альтернатив: производится попарное сравнение альтернатив между собой с целью выбора наиболее предпочтительной, причем критериальная функция не используется. При сравнении применяются бинарные отношения эквивалентности, порядка и доминирования.

        Напомним элементарные свойства бинарных отношений, которые используются при построении указанных сложных отношений.