|
|
Лекции по ПСУ, ч.2. Лекция 1 Критериальный язык описания задачи выбора
Отношение эквивалентности. Отношение R на множестве Х называется отношением эквивалентности, если оно одновременно рефлексивно, симметрично и транзитивно. Таким образом, отношение эквивалентности объединяет элементарные свойства 1,3 и 6. Обозначение:
x у.
Примеры отношения эквивалентности: «четность» на множестве натуральных чисел – при этом все четные числа считаются эквивалентными; «быть студентами одной учебной группы» – каждый из студентов группы является элементом множества студентов данного института, и все они эквивалентны друг другу.
Отношение нестрогого порядка. Отношение R на множестве Х называется отношением нестрогого порядка, если оно одновременно рефлексивное, антисимметричное и транзитивное, т.е объединяет в себе свойства 1, 5 и 6. Обозначение:
x ≤ у.
Отношение строгого порядка. Отношение R на множестве Х называется отношением строгого порядка, если оно одновременно антирефлексивное, асимметричное и транзитивное, т.е. объединяет в себе свойства 2, 4 и 6. Иначе отношение нестрогого порядка можно рассматривать как объединение отношений строгого порядка и эквивалентности, т.е. С и А. Обозначение:
x < y.
Отношение доминирования. Отношение R на множестве Х называется отношением доминирования, если оно обладает одновременно свойствами антирефлексивности и асимметричности (свойства 2 и 4). Отношение строгого порядка – частный случай отношения доминирования, при котором имеет место еще и транзитивность. Если элемент x доминирует (т.е. в каком-то смысле явно превосходит) над элементом y, то это обозначается следующим образом:
x >> у .
5.3. Модель принятия решений на основе бинарных отношений
Отношения порядка и эквивалентности позволяют создать модель такого важного вида деятельности, как принятие решений (выбор). Выбор приходится осуществлять очень часто и в самых различных ситуациях – от бытовых случаев до проектирования сложных технических систем. Бинарные отношения позволяют сравнивать между собой различные варианты (которые называются альтернативами), являющиеся элементами множества X, и выбирать из двух более предпочтительную альтернативу. Так, в случае конечных множеств X удобно находить наилучшие альтернативы с помощью графа предпочтений, стрелки которого направлены в сторону менее предпочтимой альтернативы (рис. 22). Выделенные вершины графа, из которых ребра (стрелки) только выходят (на рисунке это альтернативы 1 и 5), – это так называемые недоминируемые (наилучшие) альтернативы.
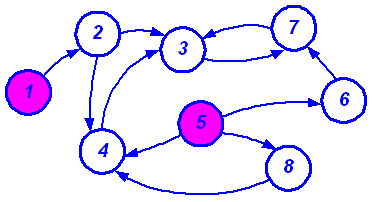
Рис. 22. Пример графа предпочтений
Если граф сильно транзитивен (т.е. транзитивен и по наличию, и по отсутствию стрелок) и антирефлексивен (отсутствуют петли), то такой выбор сводится к однокритериальному выбору. Другие ситуации выбора можно описать другими типами графов.
Лекция №5
6. Эволюционные методы
Эволюционные методы(ЭМ) предназначены для поиска предпочтительных решений и основаны на статистическом подходе к исследованию ситуаций и итерационном приближении к искомому состоянию систем.
В отличие от точных методов математического программирования ЭМ позволяют находить решения, близкие к оптимальным, за приемлемое время, а в отличие от известных эвристических методов оптимизации – характеризуются существенно меньшей зависимостью от особенностей приложения (т. е. более универсальны) и в большинстве случаев обеспечивают лучшую степень приближения к оптимальному решению. Универсальность ЭМ определяется также применимостью к задачам с неметризуемым пространством управляемых переменных (т. е. среди управляемых переменных могут быть и лингвистические).
6.1. Классификация эволюционных методов
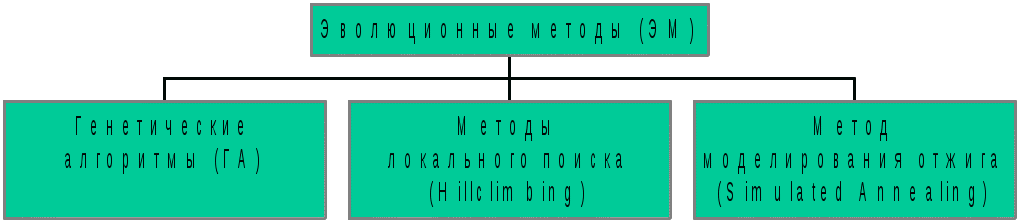
Рис. 23. Классификация эволюционных методов
6.2. Генетические алгоритмы
Важнейшим частным случаем ЭМ являются генетические методы и алгоритмы. Генетические алгоритмы (ГА) основаны на поиске лучших решений с помощью наследования и усиления полезных свойств множества объектов определенного приложения в процессе имитации их эволюции.
Свойства объектов представлены значениями параметров, объединяемыми в запись, называемую в ЭМ хромосомой. В ГА оперируют хромосомами, относящимися к множеству объектов – популяции. Имитация генетических принципов – вероятностный выбор родителей среди членов популяции, скрещивание их хромосом, отбор потомков для включения в новые поколения объектов на основе оценки целевой функции – ведет к эволюционному улучшению значений целевой функции (функции полезности) от поколения к поколению.
Для применения ГА необходимо:
1) выделить совокупность свойств объекта, характеризуемых внутренними параметрами и влияющих на его полезность, т. е. выделить множество управляемых параметров X= (x1, х2, ..., хn); среди хiмогут быть величины различных типов (real, integer, Boolean, enumeration). Наличие нечисловых величин (enumeration) обусловливает возможность решения задач не только параметрической, но и структурной оптимизации;
2) сформулировать количественную оценку полезности вариантов объекта – функцию полезности F. Если в исходном виде задача многокритериальна, то такая формулировка означает выбор скалярного (обобщенного) критерия;
3) разработать математическую модель объекта, представляющую собой алгоритм вычисления F для заданного вектора Х;
4) представить вектор Х в форме хромосомы – записи следующего вида:
X= (x1, х2, ..., хn).
В ГА используется следующая терминология:
ген – управляемый параметр хi;
аллель – значение гена;
локус – позиция, занимаемая геном в хромосоме;
генотип – экземпляр хромосомы, генотип представляет совокупность внутренних параметров проектируемого с помощью ГА объекта;
генофонд – множество всех возможных генотипов;
функция полезности(приспособленности) F – целевая функция;
фенотип – совокупность генотипа и соответствующего значения F, под фенотипом часто понимают совокупность выходных параметров синтезируемого с помощью ГА объекта.
6.3. Простой генетический алгоритм
Вычислительный процесс начинается с генерации исходного поколения – множества, включающего N хромосом, N – размер популяции. Генерация выполняется случайным выбором аллелей каждого гена.
Далее организуется циклический процесс смены поколений.
for (k=0; k
{for j=0; j
{Выбор родительской пары хромосом;
Кроссовер;
Мутации;
Оценка функции полезности F потомков;
Селекция;
}
Замена текущего поколения новым;
}
Для каждого витка внешнего цикла генетического алгоритма выполняется внутренний цикл, на котором формируются экземпляры нового (следующего за текущим) поколения. Во внутреннем цикле повторяются операторы выбора родителей, кроссовера родительских хромосом, мутации, оценки приспособленности потомков, селекции хромосом для включения в очередное поколение.
Рассмотрим алгоритмы выполнения операторов в простом ГА.
Выбор родителей.Этот оператор имитирует естественный отбор, если отбор в родительскую пару хромосом с лучшими значениями функции полезности F более вероятен.
Н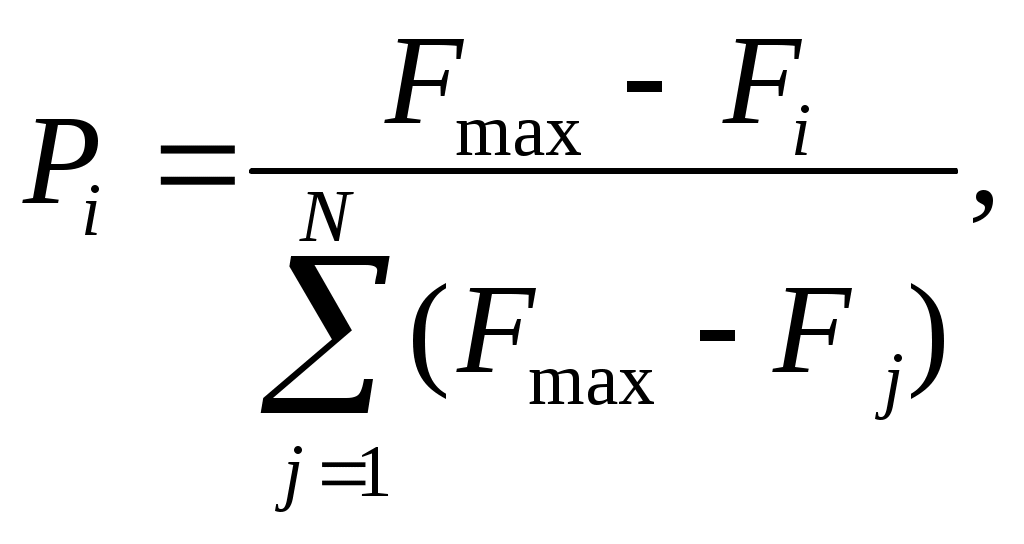 апример, пусть F требуется минимизировать. Тогда вероятность Рiвыбора родителя с хромосомой Сiможно рассчитать по формуле: апример, пусть F требуется минимизировать. Тогда вероятность Рiвыбора родителя с хромосомой Сiможно рассчитать по формуле:
где Fmax – наихудшее значение целевой функции F среди экземпляров (членов) текущего поколения, Fi – значение целевой функции i-го экземпляра.
Правило, соответствующее данной формуле, называют правилом колеса рулетки. Если в колесе рулетки выделить секторы, пропорциональные значениям Fmax – Fi , то вероятности попадания в них суть Рi,определяемые в соответствии с данной формулой (рис. 24).
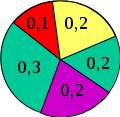
Рис. 24. К правилу колеса рулетки
Пример (выбор родителей). Пусть N =4, значения Fiи Рiприведены в таблице 1.
Таблица 1
i
|
Fi
|
Fmax–Fi
|
Pi
|
1
|
2
|
5
|
0,5
|
2
|
7
|
0
|
0
|
3
|
6
|
1
|
0,1
|
4
|
3
|
4
|
0,4
|
В соответствии с правилом выбирается кандидатура родителя с номером i=1, так как для него вероятность максимальна: Рi=0,5 (рис. 25).
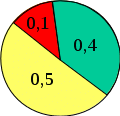
Рис. 25. Разбиение на секторы колеса рулетки для рассмотренного выше примера
Кроссовер (скрещивание).Кроссовер заключается в передаче участков генов от родителей к потомкам. При простом (одноточечном) кроссовере хромосомы родителей разрываются в некоторой позиции, одинаковой для обоих родителей, выбор места разрыва равновероятен, далее происходит рекомбинация образующихся частей родительских хромосом, как это показано в таблице 2, где разрыв подразумевается между пятым и шестым локусами.
Таблица 2

Мутации.Оператор мутации выполняется с некоторой вероятностью Рм, т. е. с вероятностью Рм происходит замена аллеля случайным значением, выбираемым с равной вероятностью в области определения гена. Именно благодаря мутациям расширяется область генетического поиска.
Селекция.После каждого акта генерации пары потомков в новое поколение включается лучший экземпляр пары.
Внутренний цикл заканчивается, когда число экземпляров нового поколения станет равным N. Количество повторений G внешнего цикла чаще всего определяется автоматически по появлению признаков вырождения (стагнации) популяции, но с условием не превышения заданного лимита машинного времени.
6.4. Разновидности генетических операторов
Возможны отклонения от представленной выше в простом генетическом алгоритме схемы вычислений.
Кроссовер. Во-первых, допустимы схемы многоточечного кроссовера. Во-вторых, есть ситуации, когда на состав аллелей наложены некоторые дополнительные условия. Например, пусть в задаче разбиения графа число вершин в подграфах А1 и А2 должно быть N1и N2и пусть k-й аллель, равный 1, означает, что вершина k попадает в А1, если же k-й аллель равен 0, то в А2.
Очевидно, что число единиц в хромосоме должно равняться N1, число нулей – N2. Тогда при рекомбинации левый участок хромосомы берется от одного из родителей без изменений, а в правом участке (от другого родителя) нужно согласовать число единиц с N1тем или иным способом.
Один из способов – метод PMX (Partially Matched Crossover – частично подобранное скрещивание).
6.4.1. Метод PMX
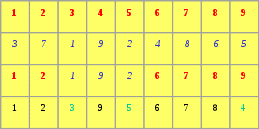
Для иллюстрации PMX рассмотрим пример двухточечного кроссовера в задаче, когда в хромосоме должны присутствовать, причем только по одному разу, все значения генов из заданного набора. Пусть в примере этот набор включает числа от 1 до 9.
В таблице 3 первые две строки представляют родительские хромосомы. Третья строка содержит хромосому одного из потомков, сгенерированного в результате применения двухточечного кроссовера (после второго и пятого локусов). Полученная хромосома не относится к числу допустимых, так как в ней значения генов 1, 2 и 9 встречаются дважды, а значения 3, 4 и 5 отсутствуют.
Четвертая строка показывает результат применения PMX. В этом методе выделяются сопряженные пары аллелей в одноименных локусах одной из рекомбинируемых частей.
В нашем примере это пары (3 и 1), (4 и 9), (5 и 2). Хромосома потомка просматривается слева – направо; если повторно встречается некоторое значение, оно заменяется на сопряженное значение.
Так, в примере в локусах 3, 5 и 9 повторно встречающиеся аллели 1, 2 и 9 последовательно заменяются на значения 3, 5 и 4.
Таблица 3
Мутации.Бывают точечными (в одном гене), макромутациями (в нескольких генах) и хромосомными (появление новой хромосомы). Обычно вероятность появления мутации указывается среди исходных данных. Но возможно автоматическое регулирование числа мутаций при их реализации только в ситуациях, когда родительские хромосомы различаются не более чем в К генах.
Селекция.После определения и положительной оценки потомка он может быть сразу же включен в текущую популяцию вместо худшего из своих родителей, при этом из алгоритма исключается внешний цикл (однако это не означает сокращения общего объема вычислений).
Другой вариант селекции – отбор после каждой операции скрещивания двух лучших экземпляров среди двух потомков и двух родителей.
Еще вариант селекции – отбор N экземпляров среди членов репродукционной группы, которая составляется из родителей, потомков и мутантов, удовлетворяющих условию Fi< t, где t – пороговое значение функции полезности. Порог может быть равен или среднему значению F в текущем поколении, или значению F особи, занимающей определенное порядковое место. При этом мягкая схема отбора – в новое поколение включаются N лучших представителей репродукционной группы. Жесткая схема отбора – в новое поколение экземпляры включаются с вероятностью qi:
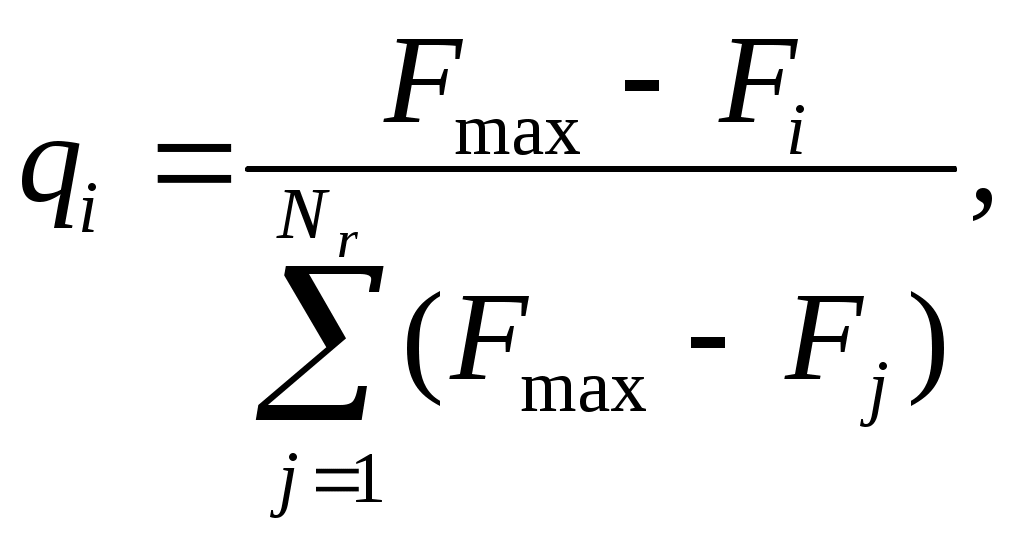
где Nr – размер репродукционной группы.
Переупорядочение.Кроме перечисленных основных операторов, находят применение некоторые дополнительные. Ких числу относится оператор переупорядочения генов – изменения их распределения по локусам.
Назначение переупорядочения связано со свойством, носящим название эпистасис. Эnucmacuc имеет место, если функция полезности зависит не только от значений генов (аллелей), но и от их позиционирования. Наличие эпистасиса говорит о нелинейности целевой функции и существенно усложняет решение задач.
Действительно, если некоторые аллели двух генов оказывают определенное положительное влияние на целевую функцию, образуя некоторую связку (схему), но вследствие эпистасиса при разрыве связки эти аллели оказывают уже противоположное влияние на функцию полезности, то разрывать такие схемы не следует. Аэто означает, что связанные эпистасисом гены желательно располагать близко друг к другу, т. е. при небольших длинах схем.
Оператор переупорядочения помогает автоматически «нащупать» такие совокупности генов (они называются хромосомными блоками, или building blocks) и разместить их в близких локусах.
6.4.2. Формирование хромосом
Возможны два подхода к формированию хромосом. Первый из них основан на использовании в качестве генов проектных параметров. Например, в задаче размещения микросхем на плате локусы соответствуют посадочным местам на плате, а генами являются номера (имена) микросхем. Другими словами, значением k-го гена будет номер микросхемы в k-й позиции.
Во втором подходе генами являются не сами проектные параметры, а номера эвристик, используемых для определения проектных параметров. Так, для задачи размещения можно применять несколько эвристик. По одной из них в очередное посадочное место нужно помещать микросхему, имеющую наибольшее число связей с уже размещенными микросхемами, по другой – микросхему с минимальным числом связей с еще не размещенными микросхемами и т. д. Генетический поиск в этом случае есть поиск последовательности эвристик, обеспечивающей оптимальный вариант размещения.
Второй подход получил название – метод комбинирования эвристик. Этот метод оказывается предпочтительным во многих случаях. Например, в задачах синтеза расписаний распределяется заданное множество работ во времени и между обслуживающими устройствами – серверами, т.е. проектными параметрами для каждой работы будут номер сервера и порядковый номер в очереди на обслуживание. |
|
|
 Скачать 4.27 Mb.
Скачать 4.27 Mb.


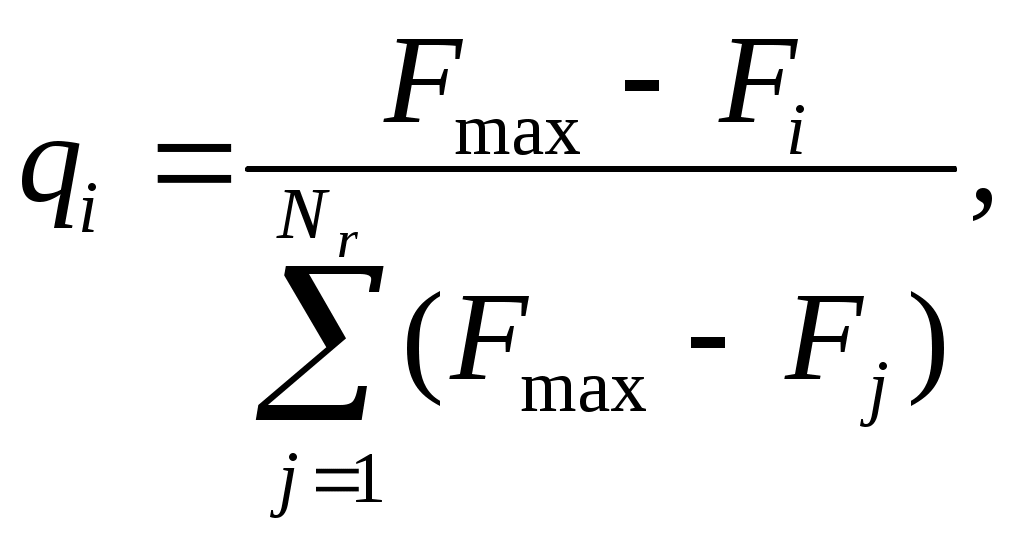



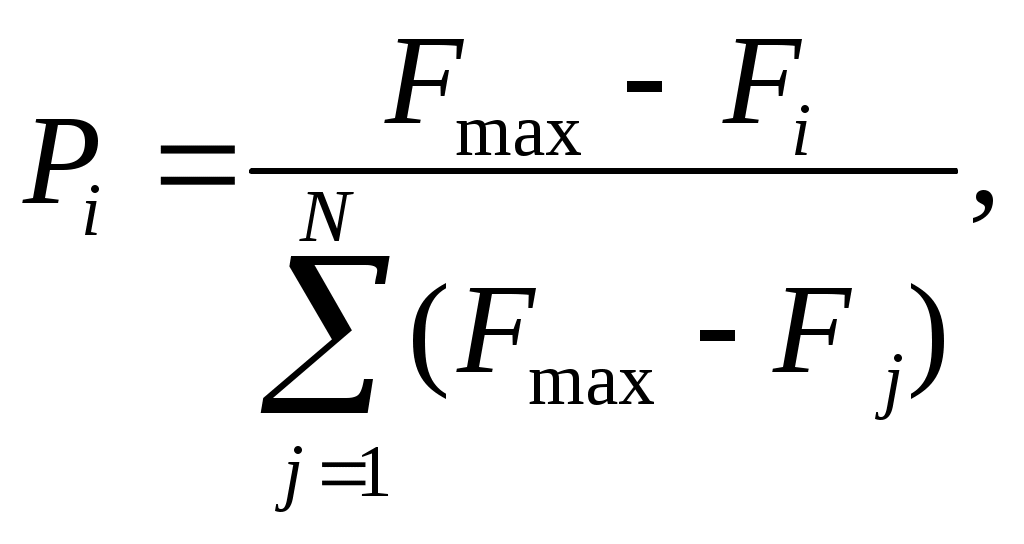 апример, пусть F требуется минимизировать. Тогда вероятность Рiвыбора родителя с хромосомой Сiможно рассчитать по формуле:
апример, пусть F требуется минимизировать. Тогда вероятность Рiвыбора родителя с хромосомой Сiможно рассчитать по формуле: 