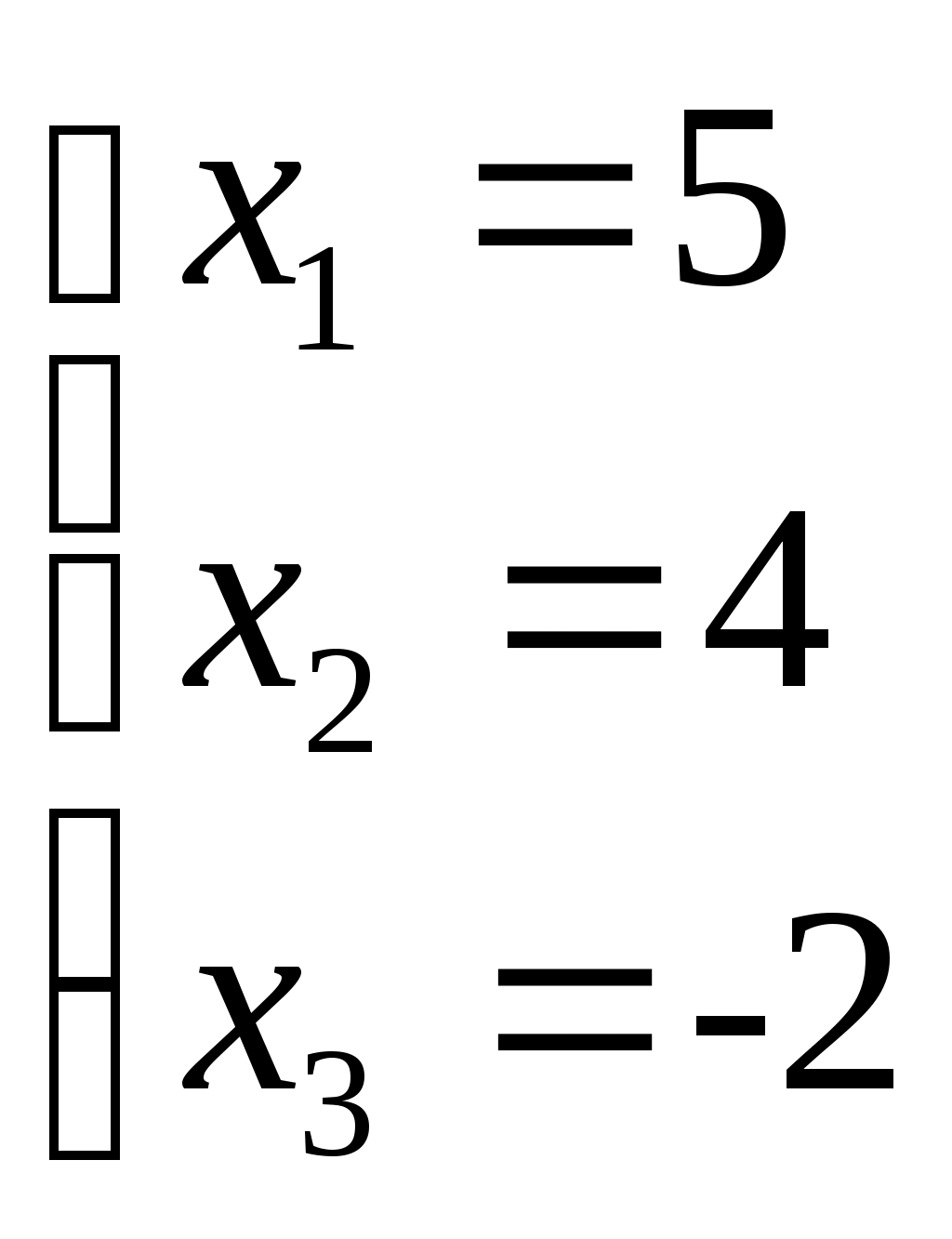|
|
1. Лекция 1-2 Элементы линейной алгебры. Лекция 1 Матрицы. Определители I. Матрицы. Определение
Элементы линейной алгебры
Лекция №1 «Матрицы. Определители»
I. Матрицы.
Определение: Матрицей называется прямоугольная таблица чисел, содержащая m строк одинаковой длины (или n столбцов одинаковой длины)
Матрицу А называют матрицей размера (m x n). Числа  , где i=1,2,…,m, j=1,2,…,n, называют элементами матрицы . , где i=1,2,…,m, j=1,2,…,n, называют элементами матрицы .
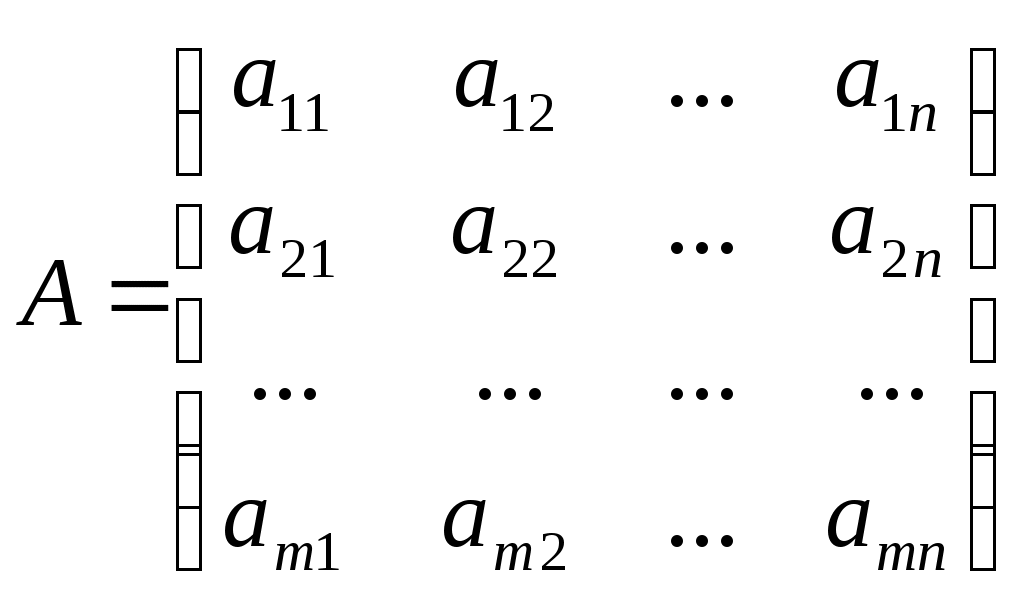
Классификация матриц
Матрицы полагаются равными при совпадении у них соответствующих элементов.
Матрица, у которой число строк равно числу столбцов называется квадратной. Квадратную матрицу размера (n x n) называют матрицей n – го порядка.
Квадратная матрица, у которой все элементы, кроме элементов главной диагонали, равны нулю, называется диагональной.
Диагональная матрица, у которой каждый элемент главной диагонали равен единице, называется единичной. Обозначается буквой Е.
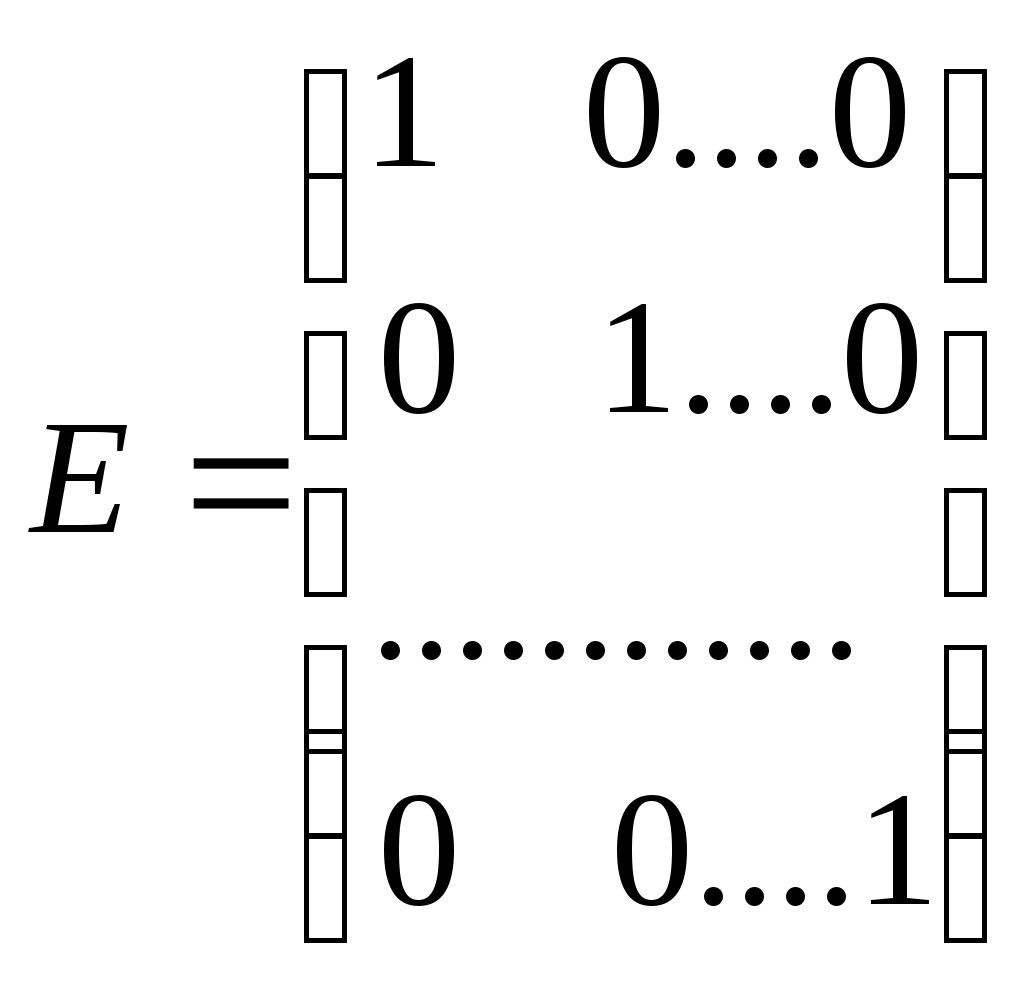
Квадратная матрица называется треугольной, если все элементы, расположенные по одну сторону от главной диагонали равны нулю.
Матрица, все элементы которой равны нулю, называется нулевой. Обозначается буквой О.
Матрица, содержащая один столбец или одну строку, называется вектором ( вектор – столбец или вектор - строка).
Матрица Ат называется транспонированной к А, если в матрице А строки заменены на столбцы соответствующих номеров
Матрица А-1 называется обратной матрице А, если выполняется условие:
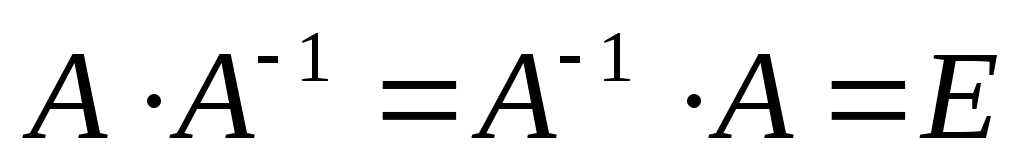
Элементарные преобразования над матрицами:
перестановка местами двух параллельных рядов матрицы;
умножение всех элементов ряда матрицы на число отличное от нуля;
прибавление ко всем элементам ряда матрицы соответствующих элементов параллельного ряда, умноженных на одно и тоже число.
Определение. Две матрицы А и В называются эквивалентными (А В), если одна из них получается из другой с помощью элементарных преобразований.
При помощи элементарных преобразований любую матрицу можно привести к матрице, у которой в начале главной диагонали стоят подряд несколько единиц, а все остальные элементы равны нулю. Такую матрицу называют канонической.

Действия над матрицами
Сумма матриц
Определение. Суммой матриц одинакового размера называется матрица, элементы которой равны сумме соответствующих элементов матриц-слагаемых. Обозначение: А+В. Аналогично определяется разность матриц.
Пример: 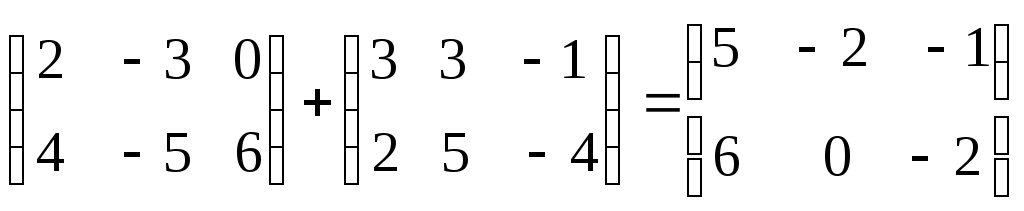
Свойства:
А+В=В+А
А+(В+С)=(А+В)+С
А+О=А
А-А=0
Умножение матрицы на число
П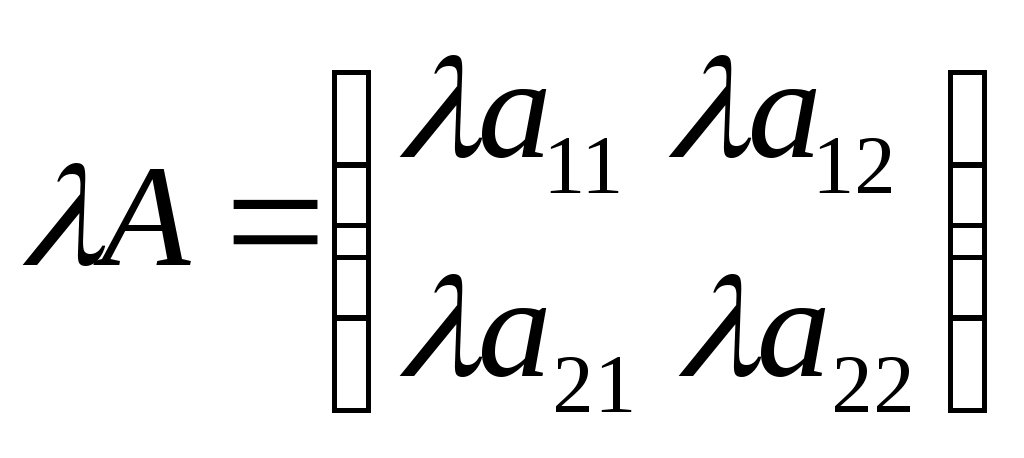 ри умножении матрицы на число, умножаются все элементы данной матрицы. ри умножении матрицы на число, умножаются все элементы данной матрицы.
Пример: 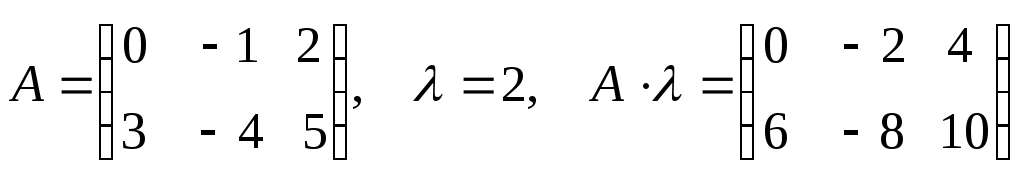
Свойства:
1·А=А
α·(А+В)= αА+ αВ
(α+β)·А= αА+ βА
α·(βА)=( αβ)·А
Произведение матриц
Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы. Такие матрицы называются согласованными (n × m и m × k).
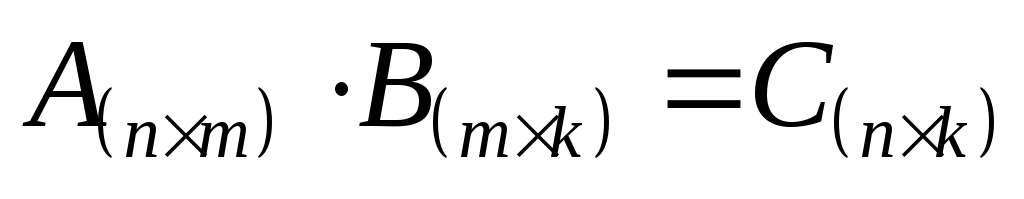
Элементом 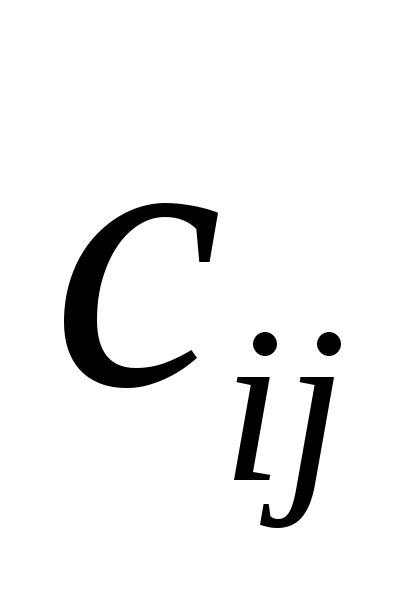 произведения двух согласованных матриц является число, которое равно сумме произведений элементов i-ой строки первой матрицы на соответствующие элементы j-го столбца второй матрицы. произведения двух согласованных матриц является число, которое равно сумме произведений элементов i-ой строки первой матрицы на соответствующие элементы j-го столбца второй матрицы.
Возможно умножение матрицы на вектор-столбец справа и на вектор-строку слева.
Примеры:
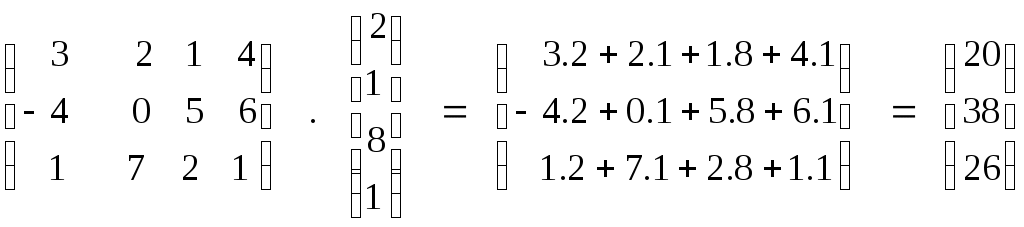
1.
2. 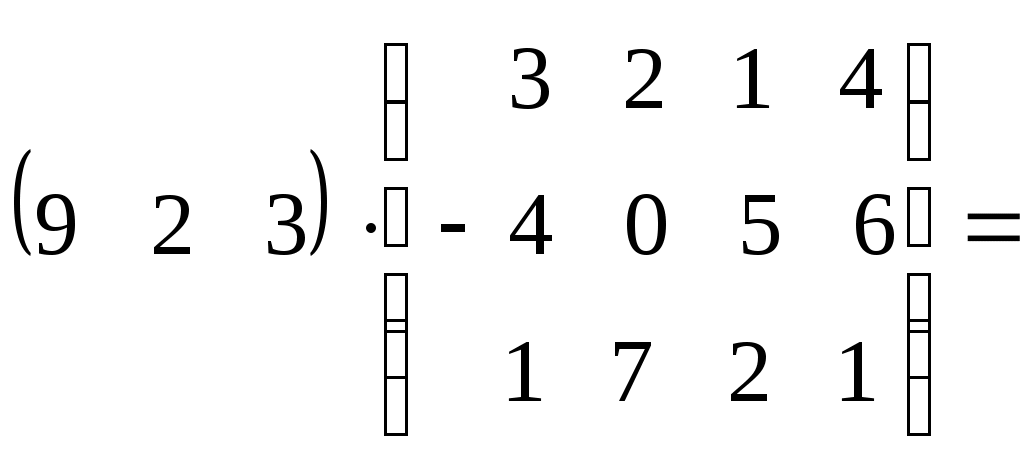
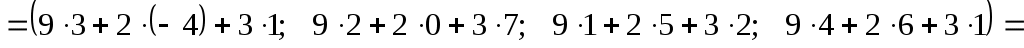
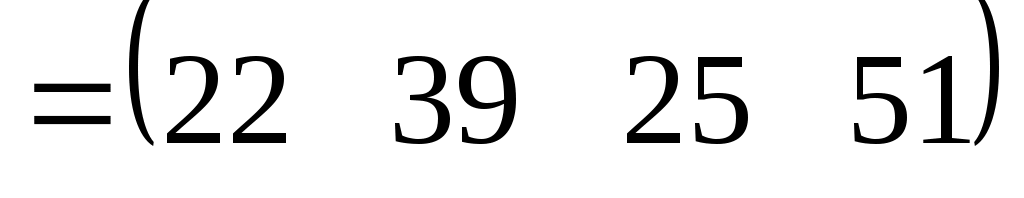
3. 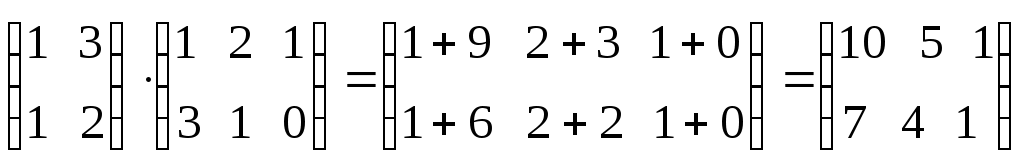
Свойствами умножения:
А × О = О
А × Е = А
А × В ≠ В × А
α (АВ) = (αА) × В = А × (αВ)
АВС = (АВ) × С = А × (ВС)
А (В + С) = АВ + АС
II. Определители
Квадратной матрице А порядка n можно сопоставить число det A, называемое ее определителем, следующим образом:
1) n = 1
А = (a1); det A = a1
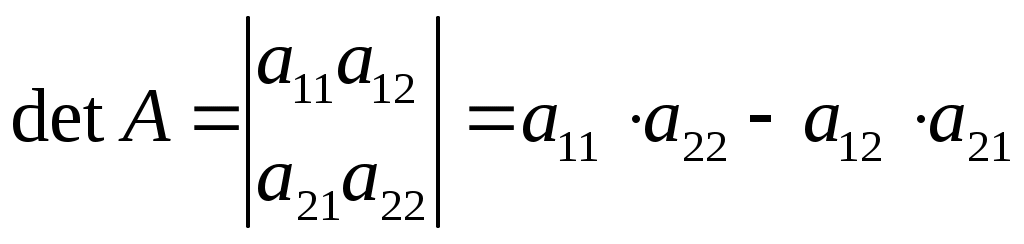
2                   ) n = 2 ) n = 2
   
 = – = –
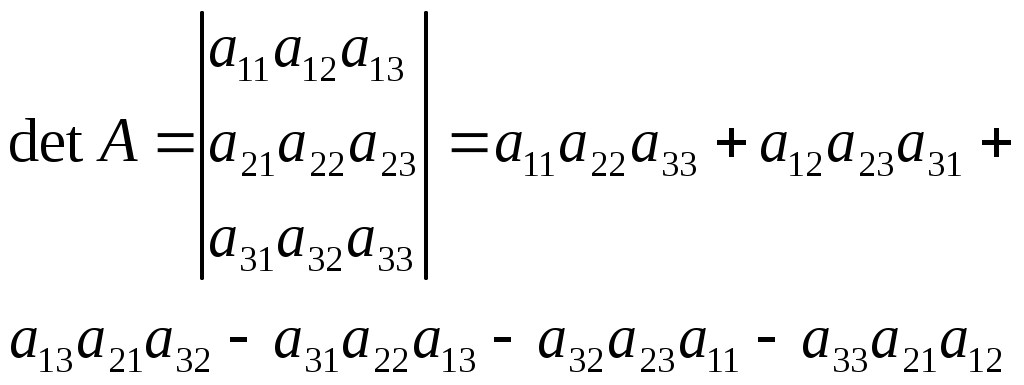
3) n = 3.

                        
   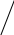 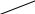 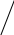   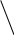   
            = – = –
Пример:
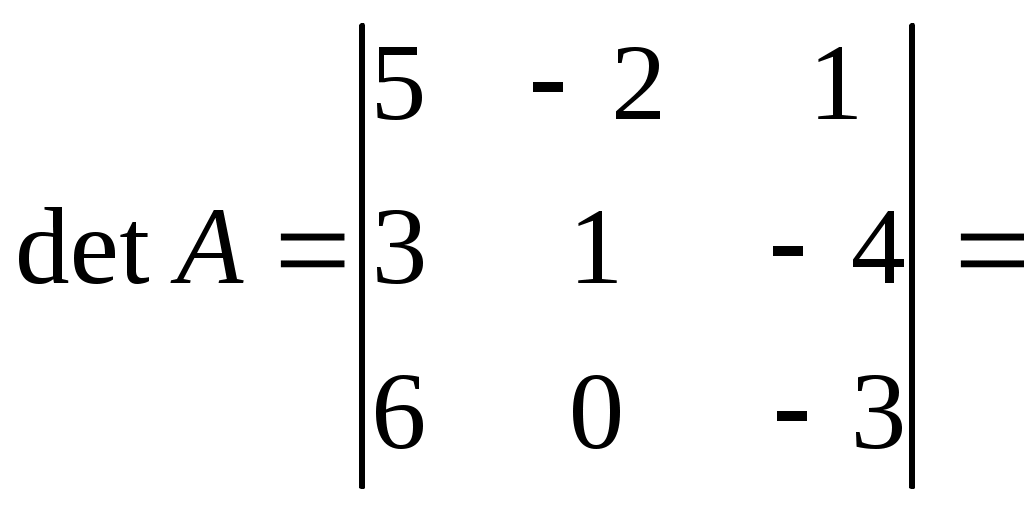
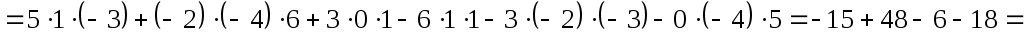 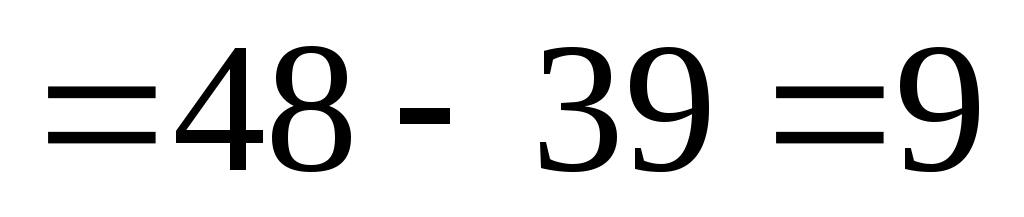
Свойства определителей
Транспонирование определителя , т.е. замена строк столбцами и наоборот, не меняет его значения.
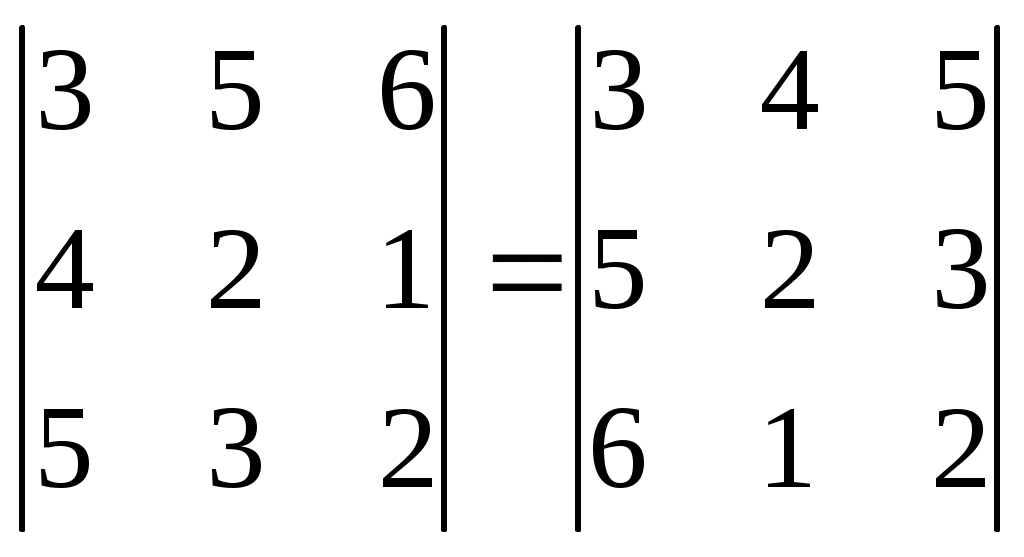
Перестановка любых двух строк (столбцов), меняет только знак определителя.
Общий множитель всех элементов одной строки (столбца) можно выносить за знак определителя.
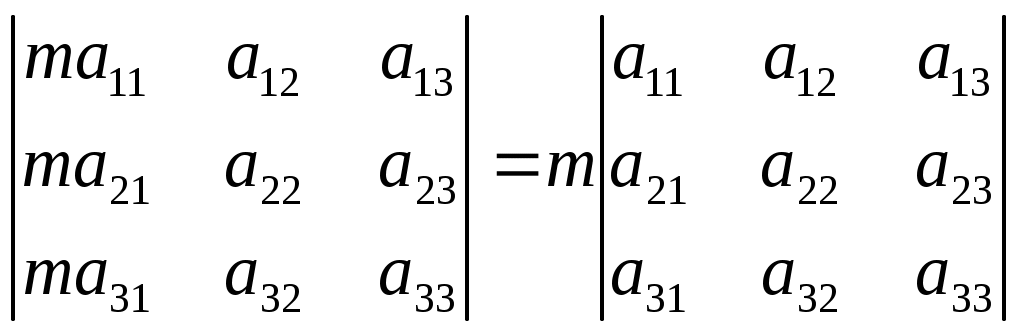
Если соответствующие элементы двух строк (столбцов) равны или пропорциональны, то определитель равен 0.
Если элементы какой-либо строки (столбца) состоят из двух слагаемых, то определитель равен сумме двух определителей, различающихся между собой только элементами одной строки (столбца), бывшими ранее отдельными слагаемыми.
Если к элементам одной строки (столбца) определителя прибавить соответственные элементы другой строки или одинаково пропорциональные им числа, то исходный определитель не изменится.
Минор элемента аij
Определение. Минором некоторого элемента aij определителя n-го порядка называется определитель порядка (n-1), полученный из исходного путем вычеркивания строки и столбца, на пересечении которых находится выбранный элемент и обозначается Мij.
 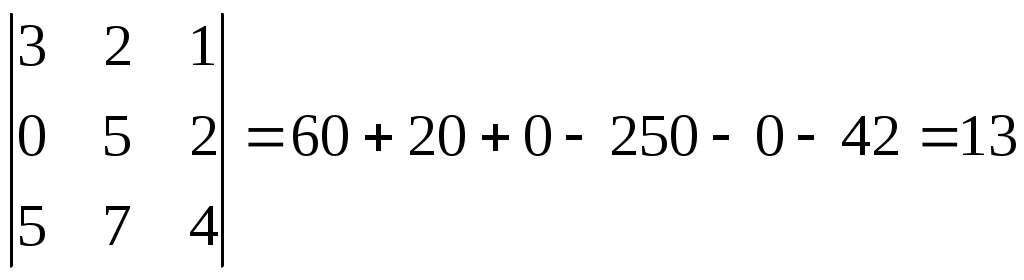 
 M23= M23=
M31=5 M14=11
Алгебраическое дополнение Aij
Определение. Алгебраическим дополнением элемента aij данного определителя называется Мij , взятый со знаком «+», если (i+j)- четное число, и со знаком «-», если (i+j)- нечетное число.
  
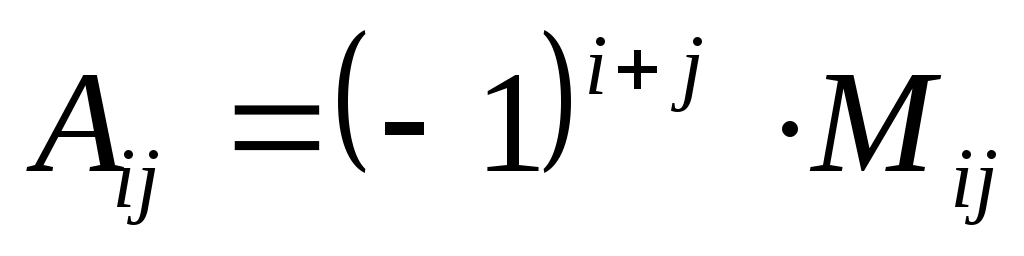

Для предыдущего примера:
А23=-М23=-13
А31=М31=5
А14=-М14=-11
Формула Лапласа.
Теорема. Определитель равен сумме произведений элементов всякой его строки (столбца) на их алгебраические дополнения.
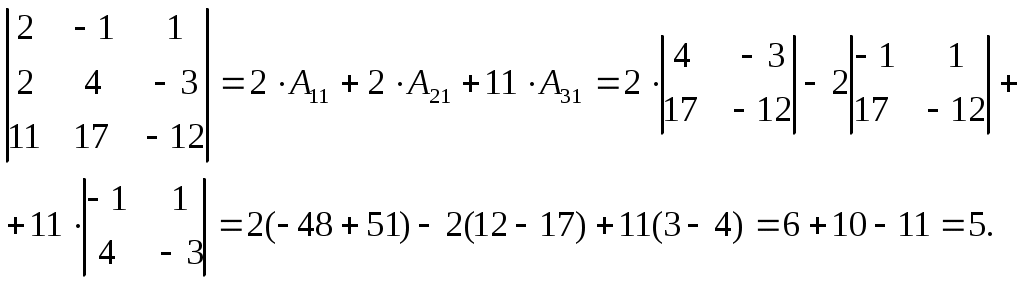
III. Ранг матрицы
Рассмотрим матрицу А размера m x n
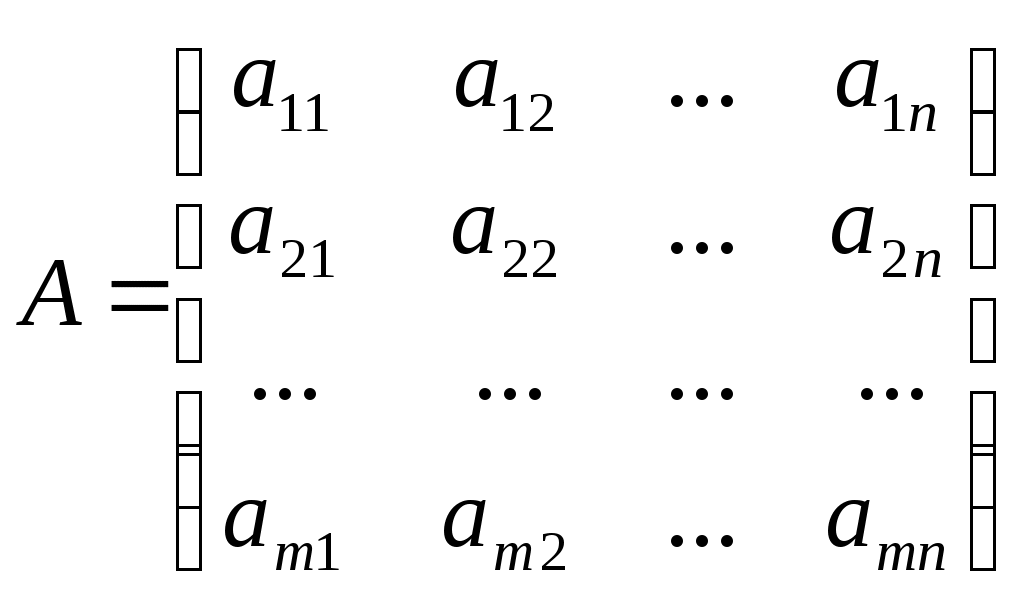
Выделим в ней k строк и k столбцов (k ≤ min(m;n)). Из элементов, стоящих на пересечении выделенных строк и столбцов, составим определитель k – го порядка. Все такие определители называются минорами этой матрицы.
Определение. Наибольший из порядков миноров данной матрицы, отличных от нуля, называется рангом матрицы. Обозначается rang A.
Пример. Найти ранг матрицы:
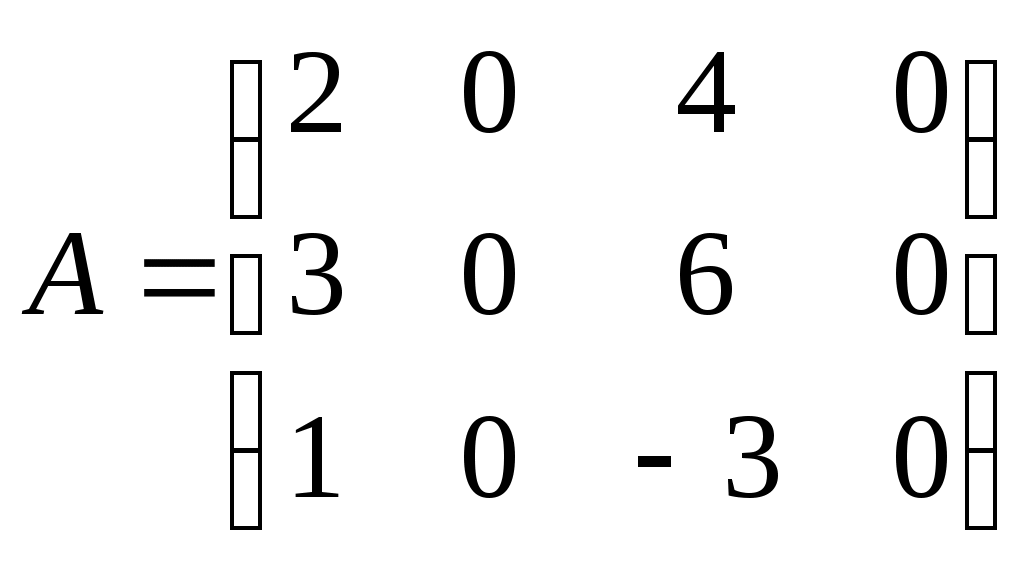
Все миноры 3-го порядка равны нулю. Есть минор 2-го порядка, отличный от нуля 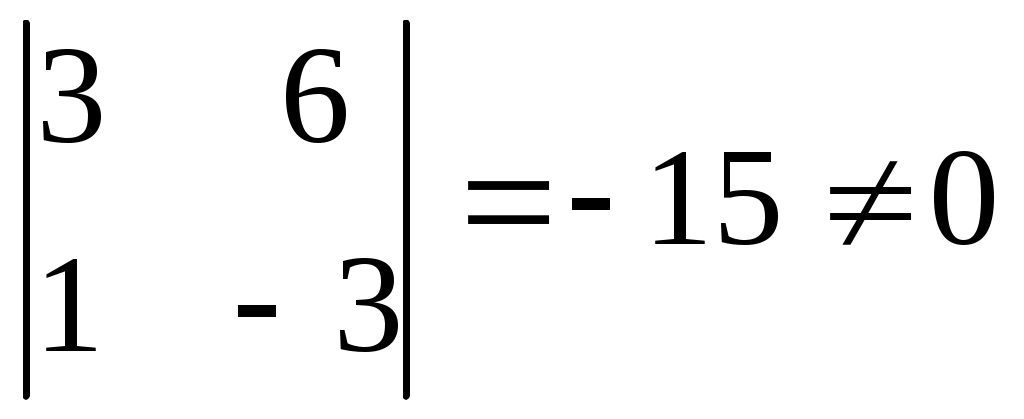 . Значит, rang A=2. . Значит, rang A=2.
Ранг канонической матрицы равен числу единиц на главной диагонали. На этом основан один из способов вычисления ранга матрицы.
Пример: найти ранг матрицы путем элементарных преобразований
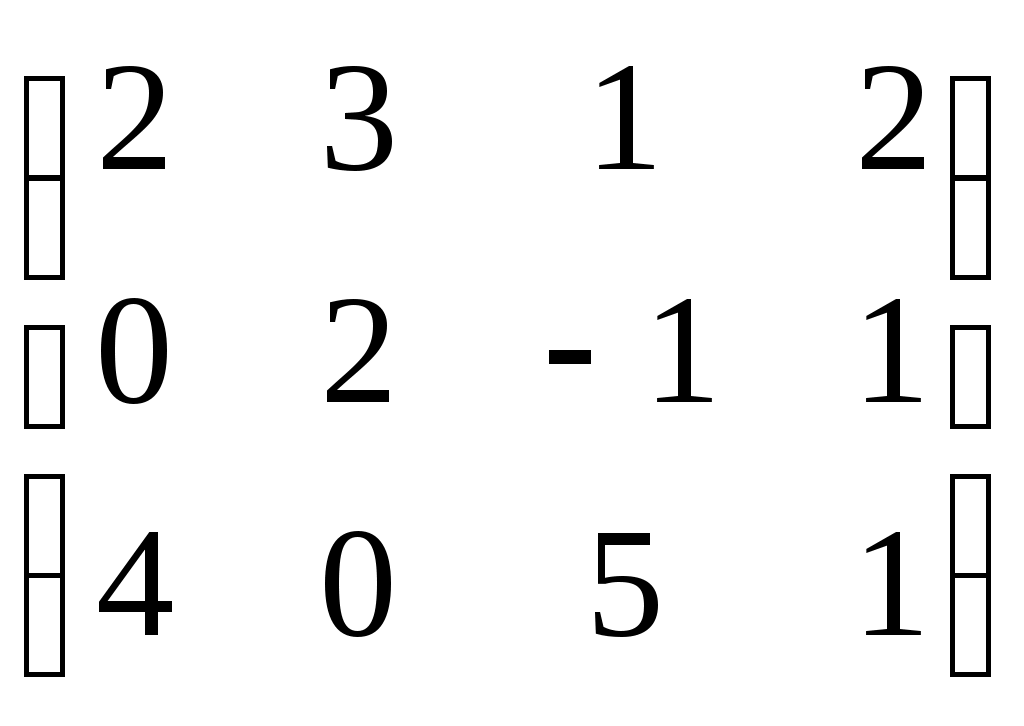
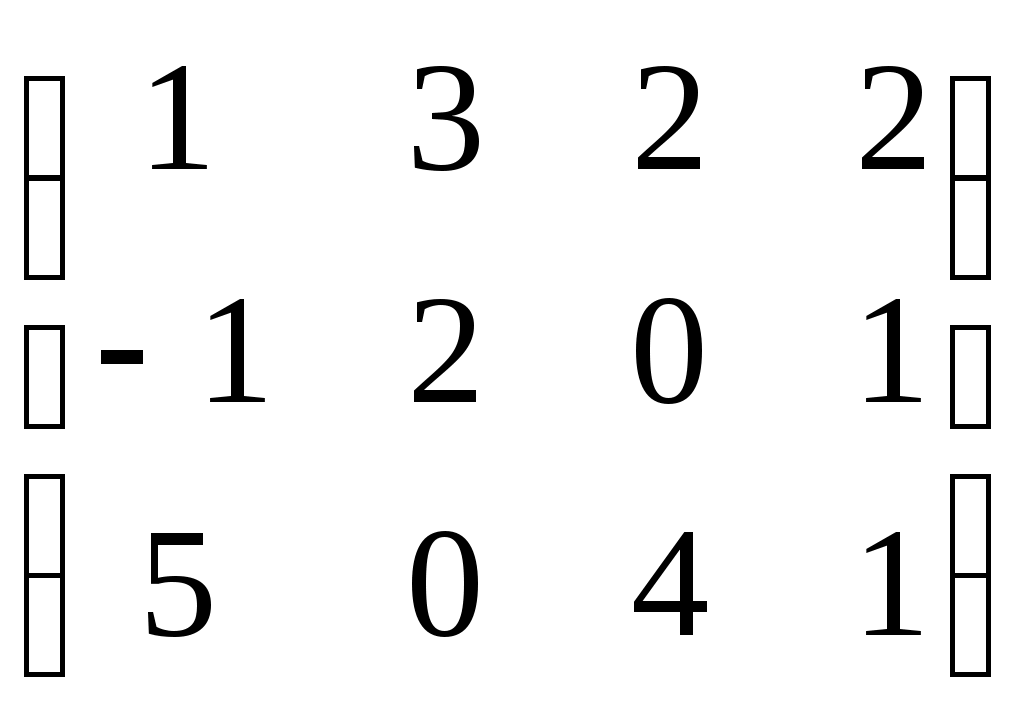
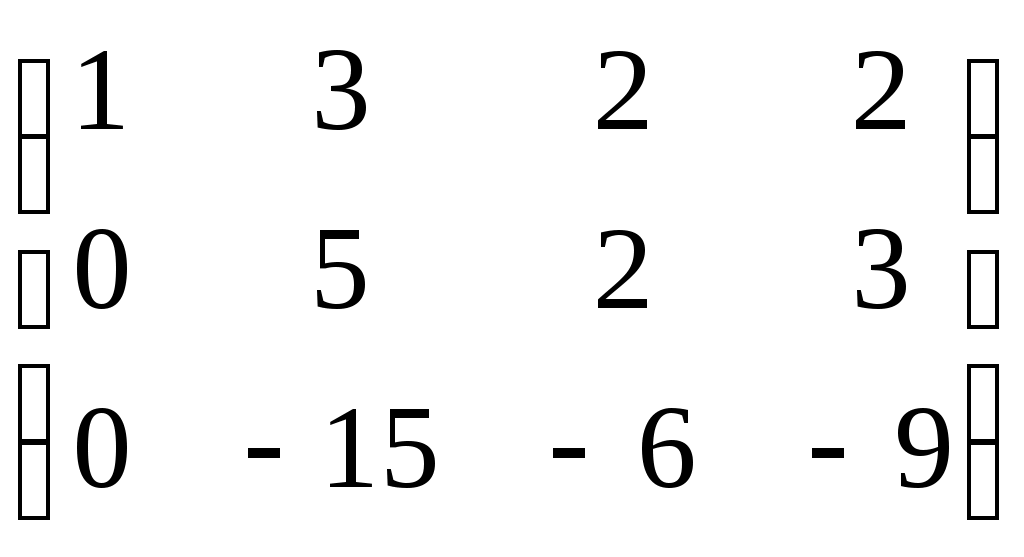
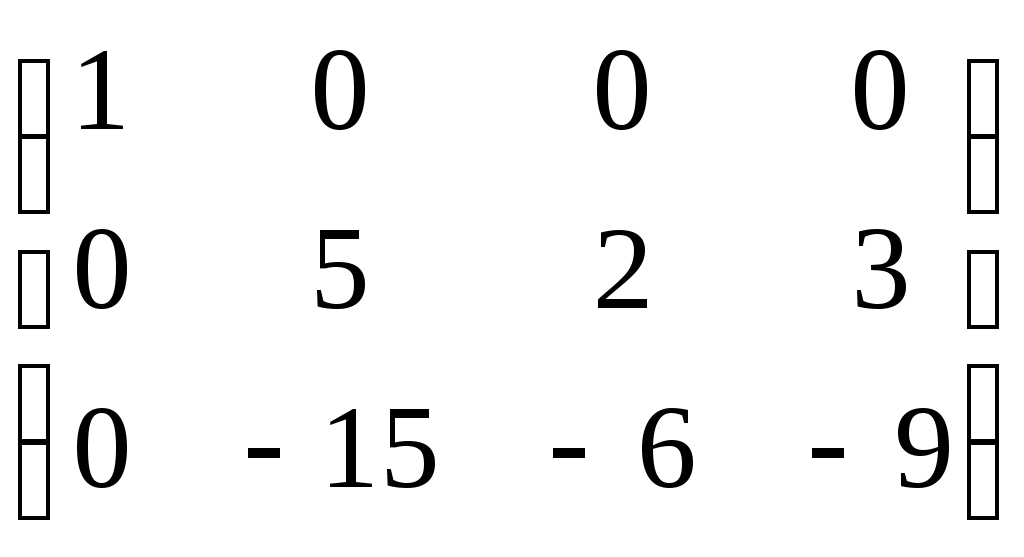
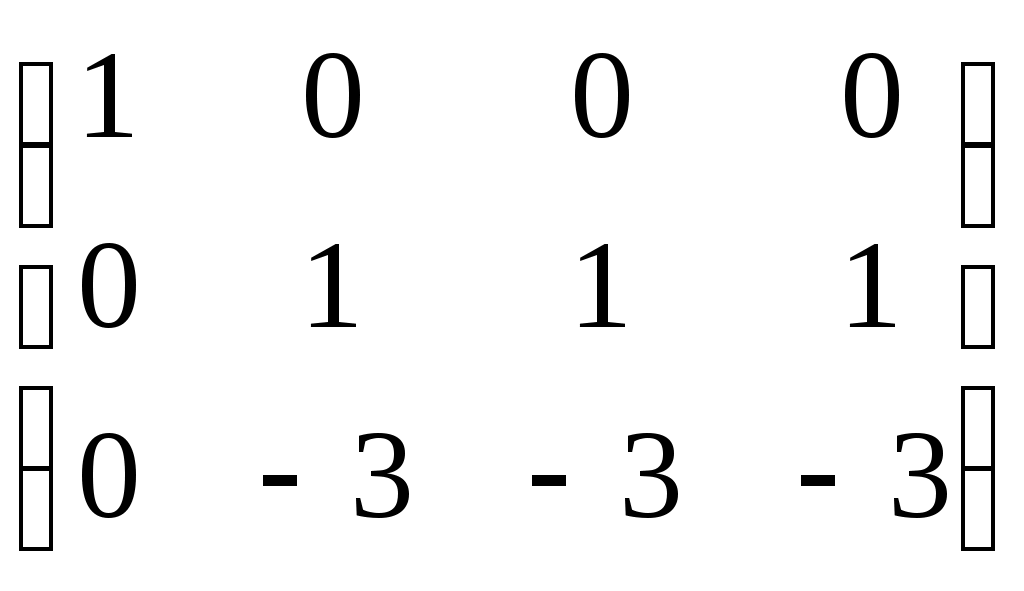
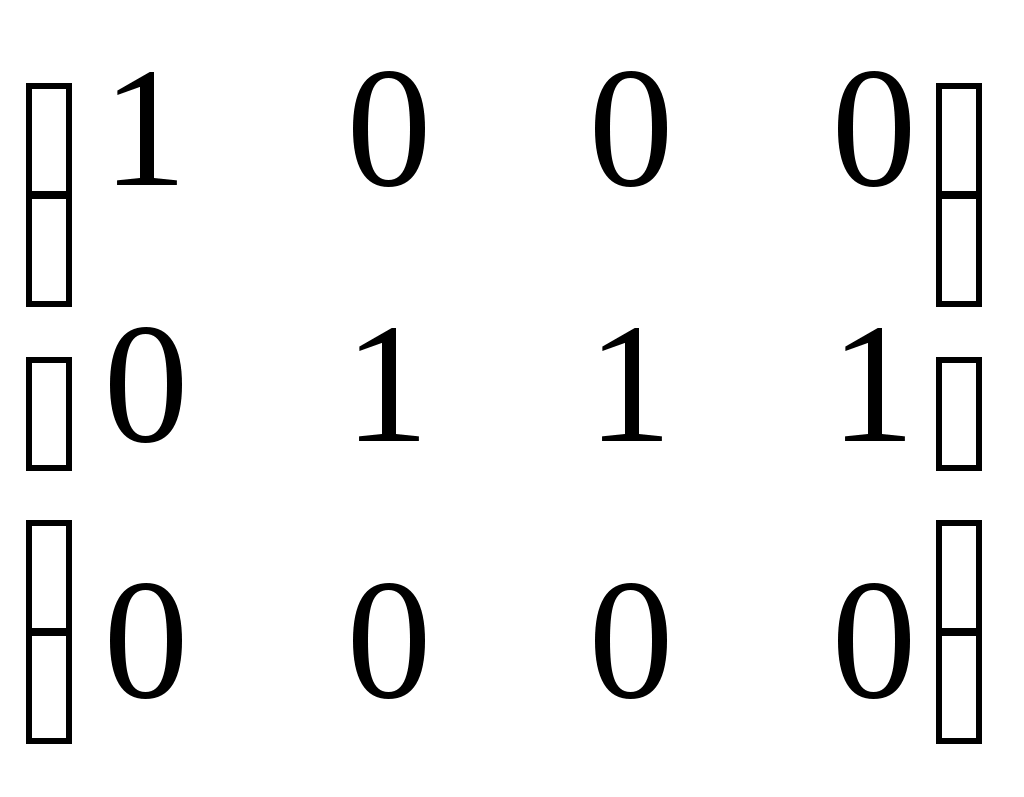
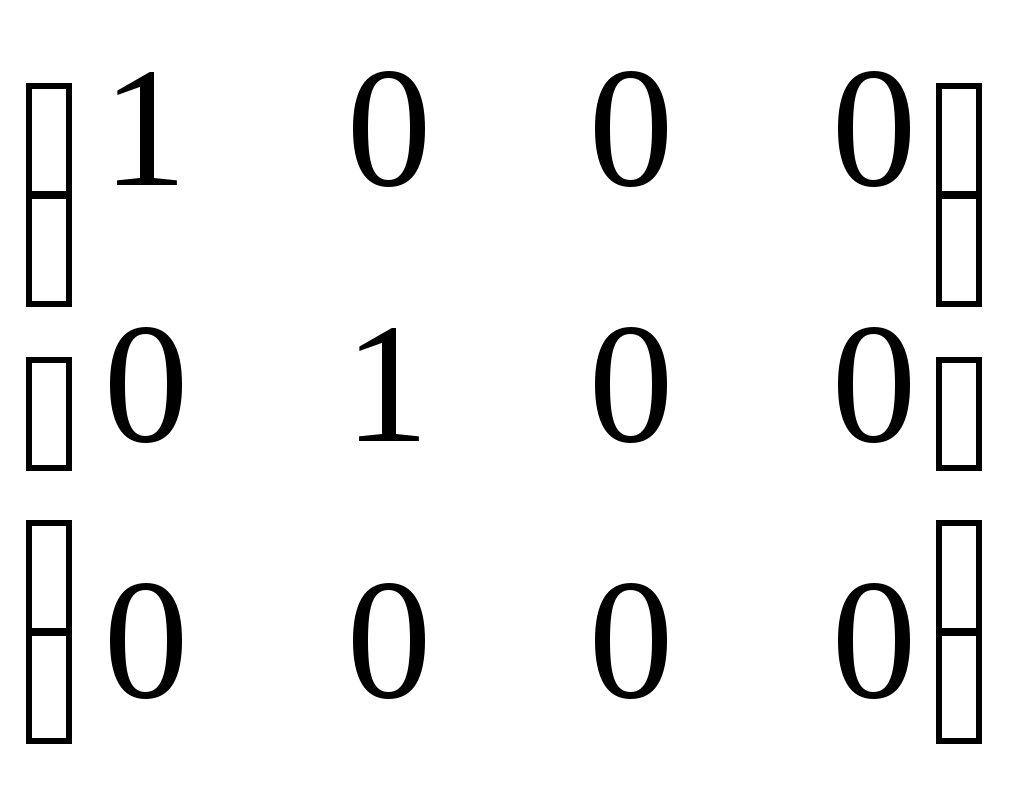 rang A=2 rang A=2
Свойства ранга матрицы:
при транспонировании матрицы ее ранг не меняется;
если вычеркнуть из матрицы нулевой ряд, то ранг матрицы не изменится;
ранг матрицы не изменяется при элементарных преобразованиях матрицы.
Лекция № 2 «Методы решения систем линейных уравнений»
1. Матричный метод
При помощи матриц очень удобно записывать произвольные системы первой степени /линейные системы/. Рассмотрим произвольную линейную систему m уравнений с n неизвестными.
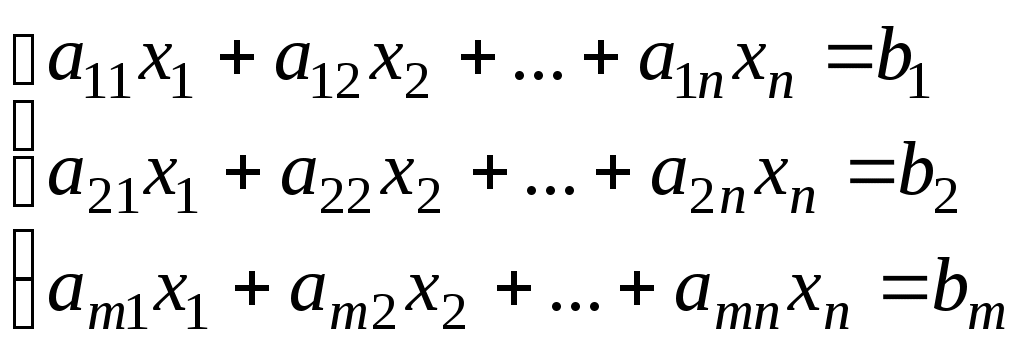 (I) (I)
Если m = n, то будем называть систему квадратной n-го порядка, если m < n - укороченной /с такими системами встречаются в экономике/, при m > n - удлиненной /такие системы встречаются в геодезии/.
Введем три матрицы: А – матрицу, составленную из коэффициентов при неизвестных /её называют матрицей системы/, Х – матрицу-столбец неизвестных, В – матрицу-столбец свободных членов.
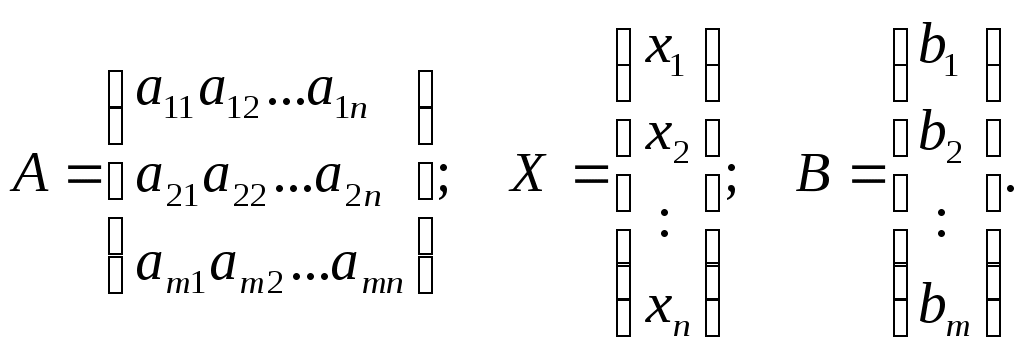
Тогда систему (I) можно записать при помощи этих матриц так:
AХ=В. (1)
Действительно, 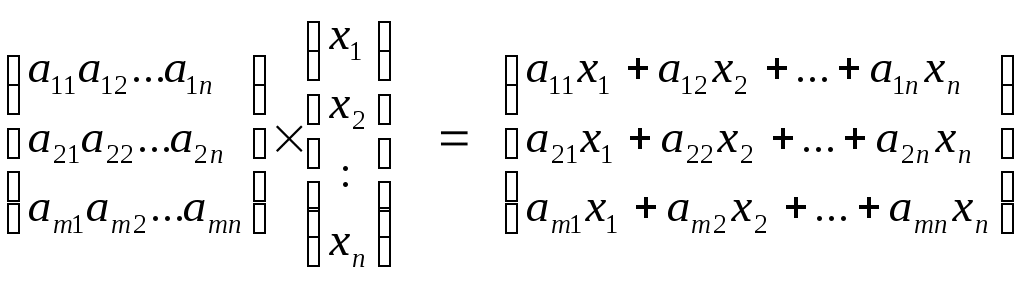
Из условия равенства матриц следует, что уравнение (1) равносильно системе (I). Матричная запись системы (1) аналогична записи уравнения с одним неизвестным ax=b, решением которого при 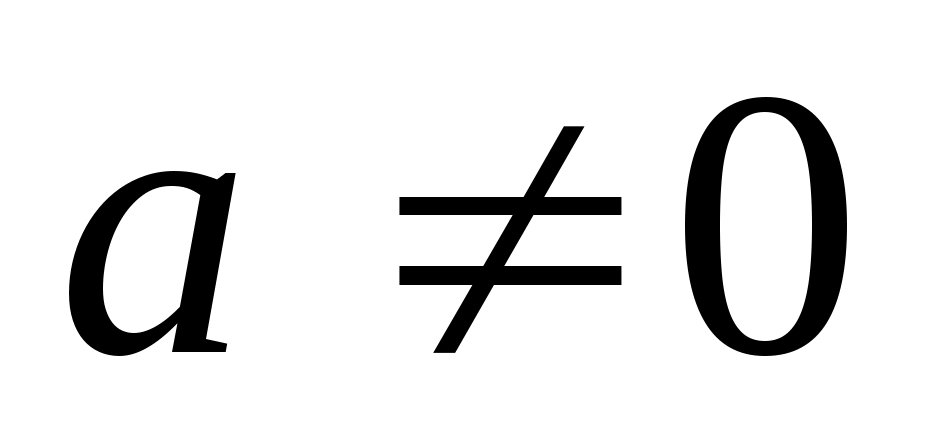 будет будет 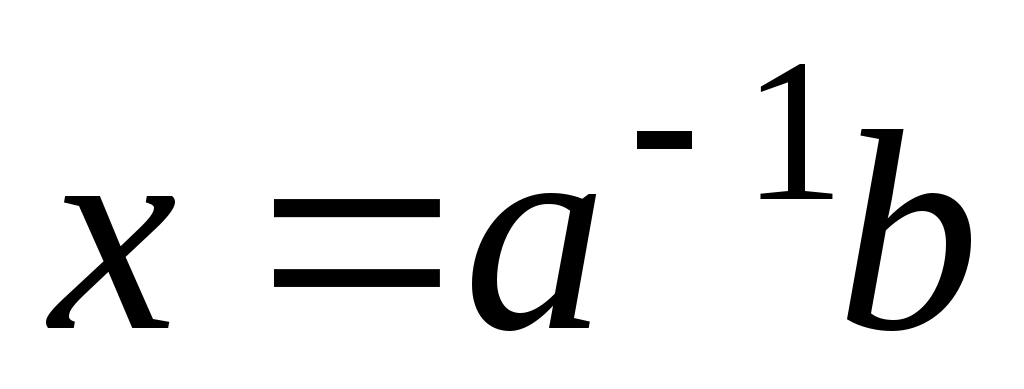 . Естественно поставить аналогичный вопрос для решения матричного уравнения AХ=В. . Естественно поставить аналогичный вопрос для решения матричного уравнения AХ=В.
Если А – невырожденная, т.е. detA≠ 0 и А имеет единственную обратную матрицу А-1, то Х = А-1 В – решение системы уравнений (I)
Алгоритм нахождения А-1:
det А ≠ 0;
составить для А матрицу из алгебраических дополнений → А*;
транспонировать А* → А*т;
домножить А*т на 1/detA → А-1.
Пример:
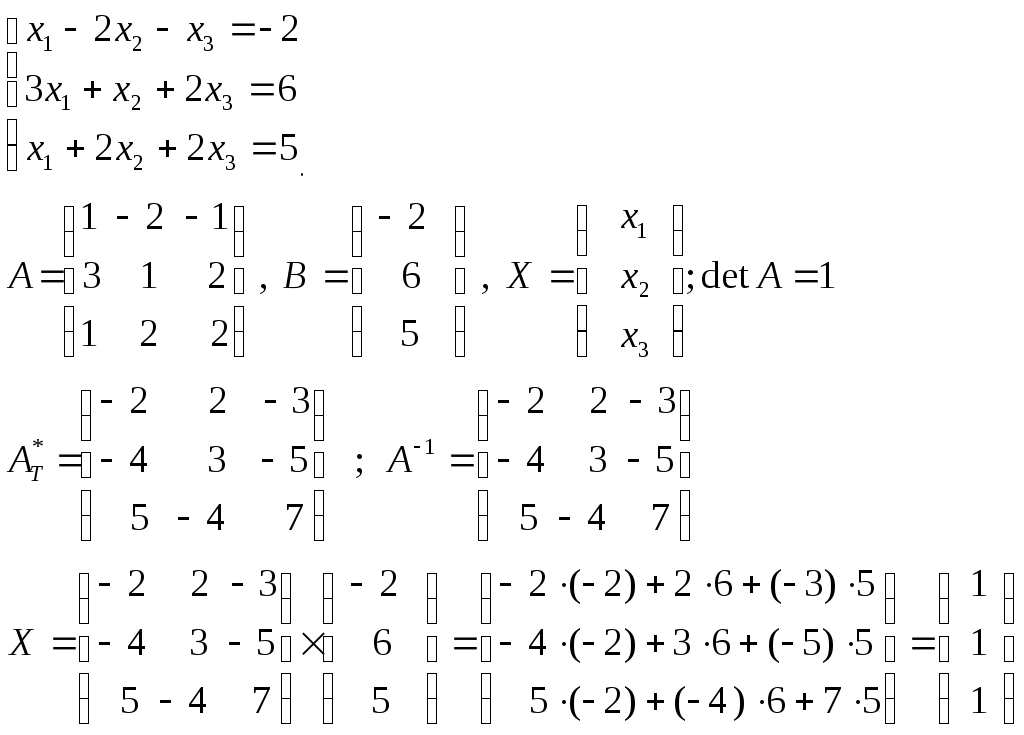
Ответ: (1; 1; 1)
2. Формулы Крамера
Теорема. Если определитель системы (D) n линейных уравнений с n неизвестными не равен нулю, то система совместна и имеет единственное решение, выражаемое по следующим формулам:
x1 = 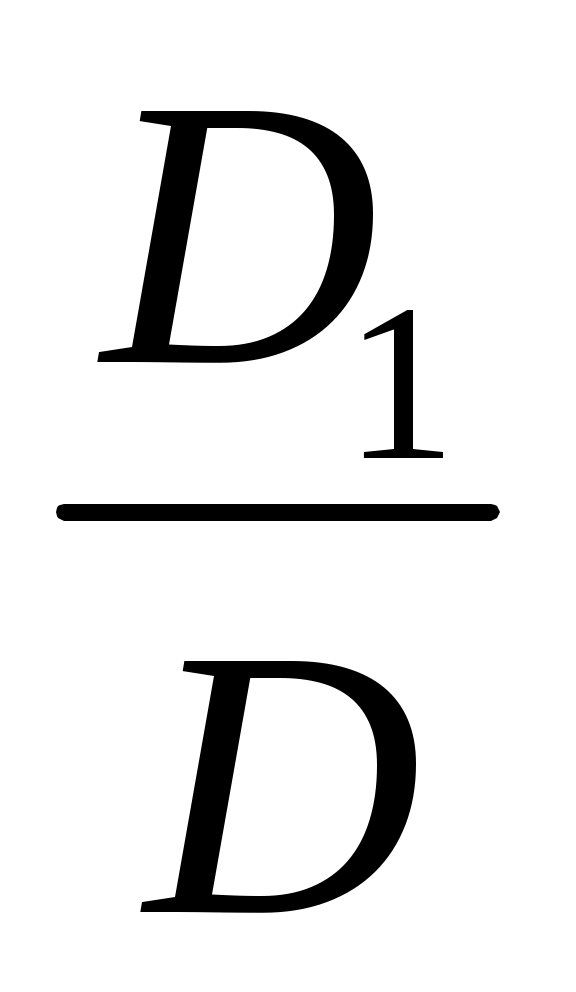 , x2 = , x2 =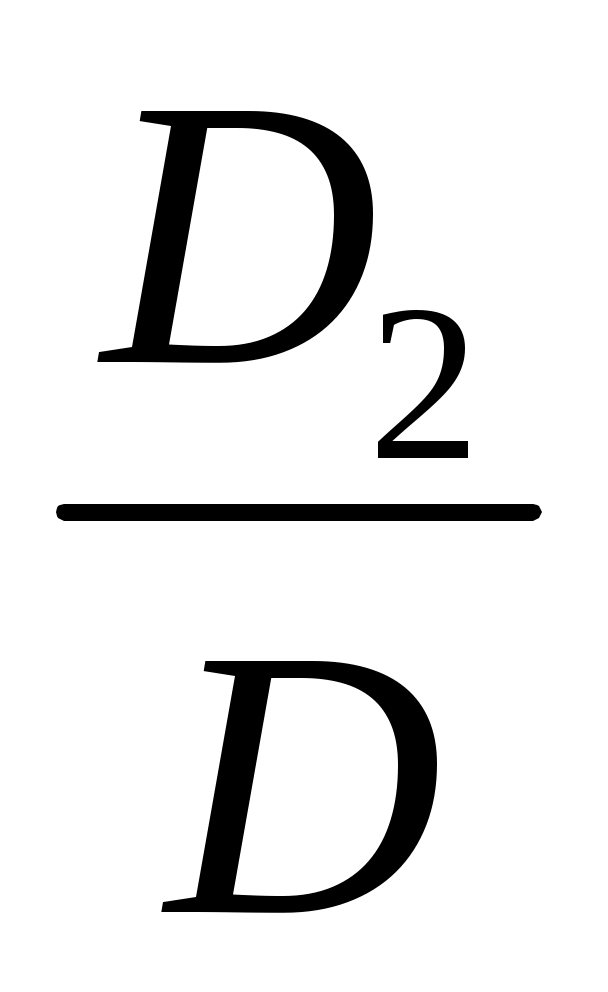 , … , xn= , … , xn=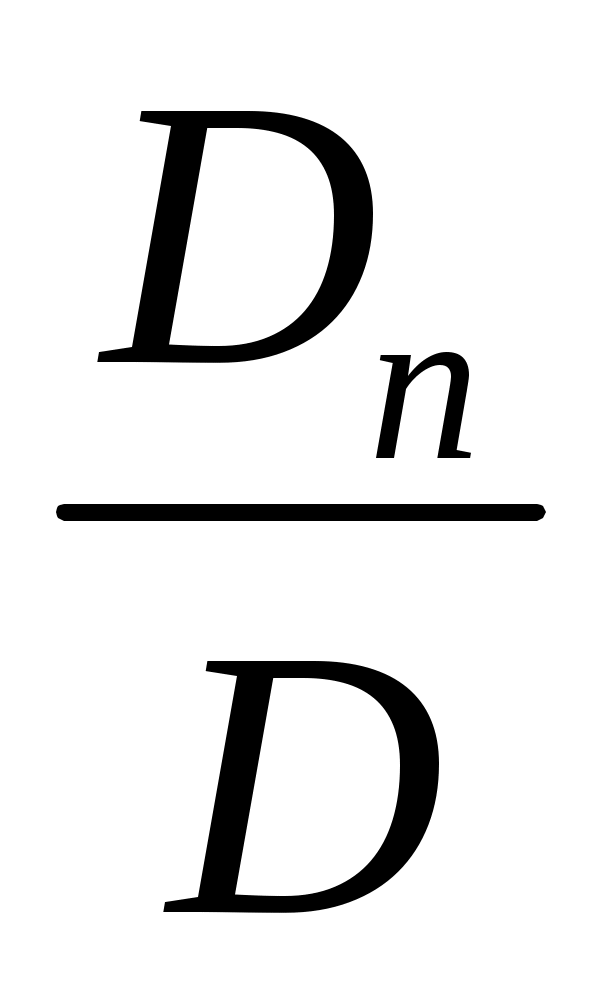 . .
Dn – это определитель, который получается из определителя системы путем замены только n-го столбца столбцом свободных коэффициентов системы.
Пример. Решите систему по формулам Крамера
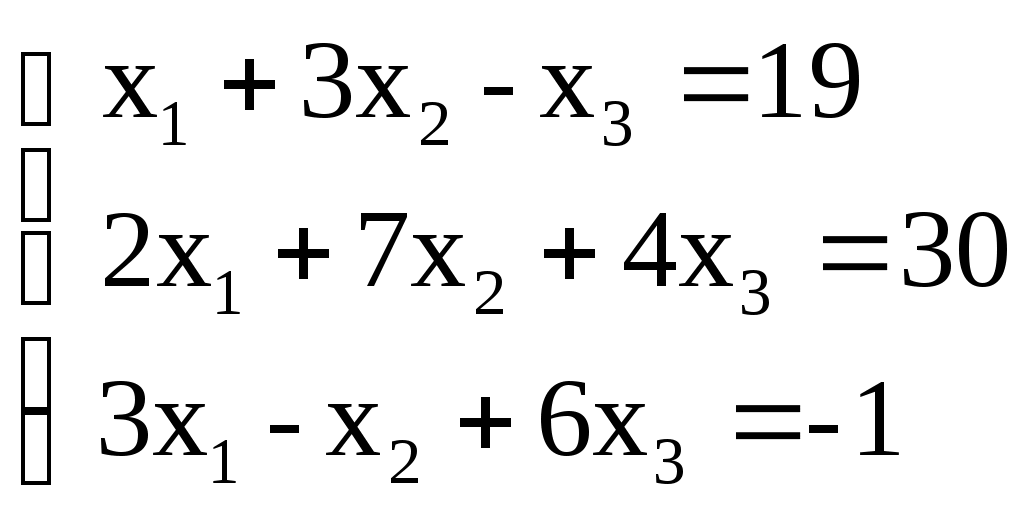
Определитель системы вычислим по правилу треугольников
D= 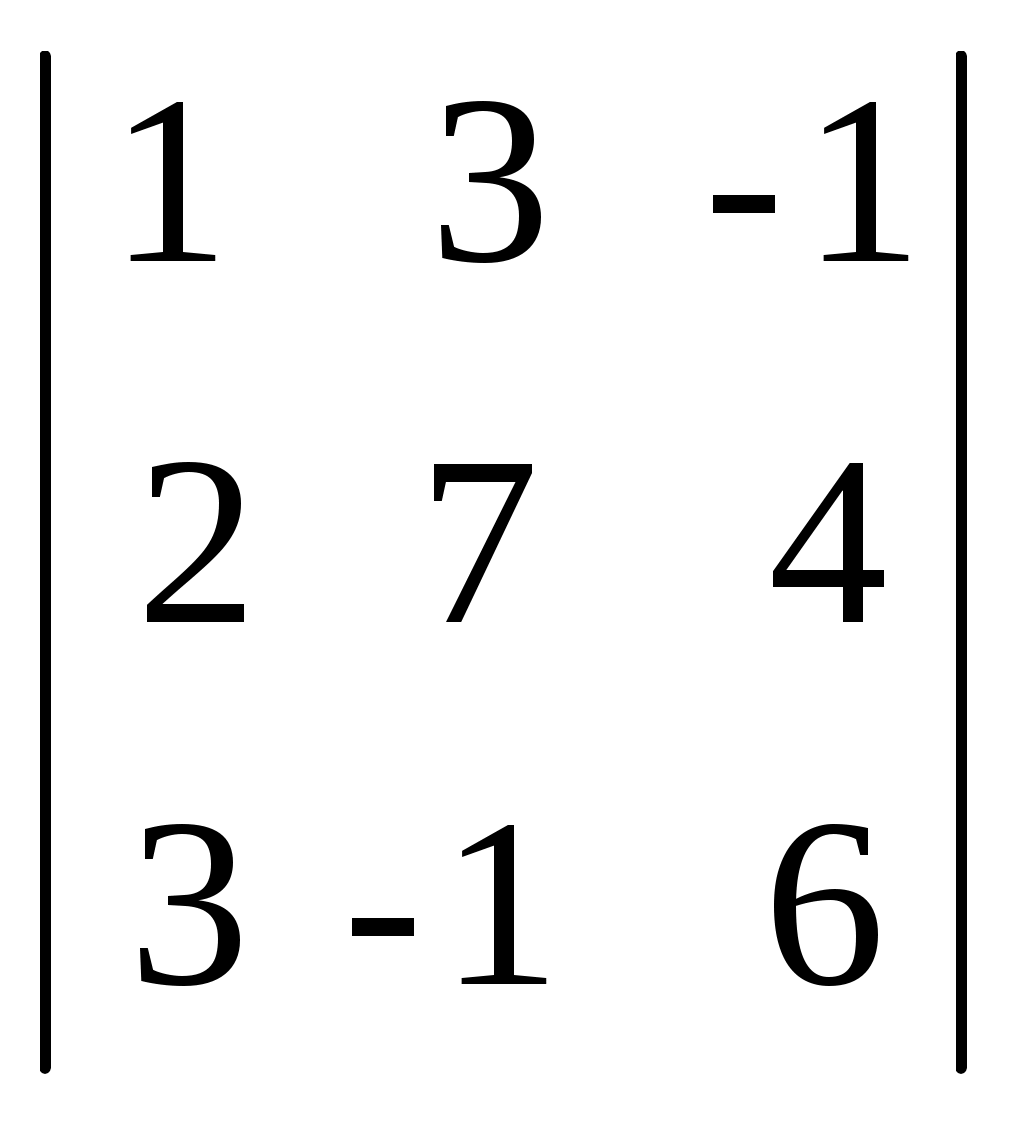 = 42+36+2-(-21+36-4) = 69 ≠ 0 = 42+36+2-(-21+36-4) = 69 ≠ 0
D1, D2, D вычислим по формуле Лапласа.
D1= 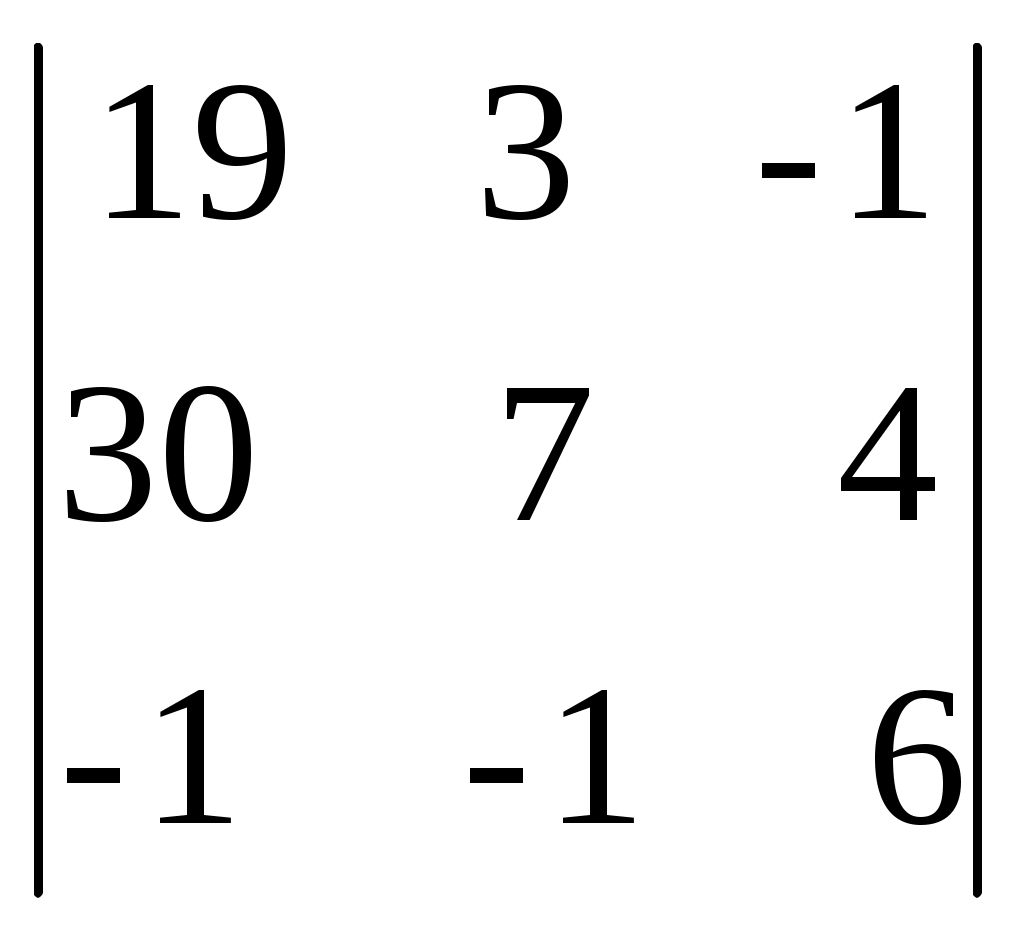 = (определитель разложим по первому столбцу) = = (определитель разложим по первому столбцу) =
19 · 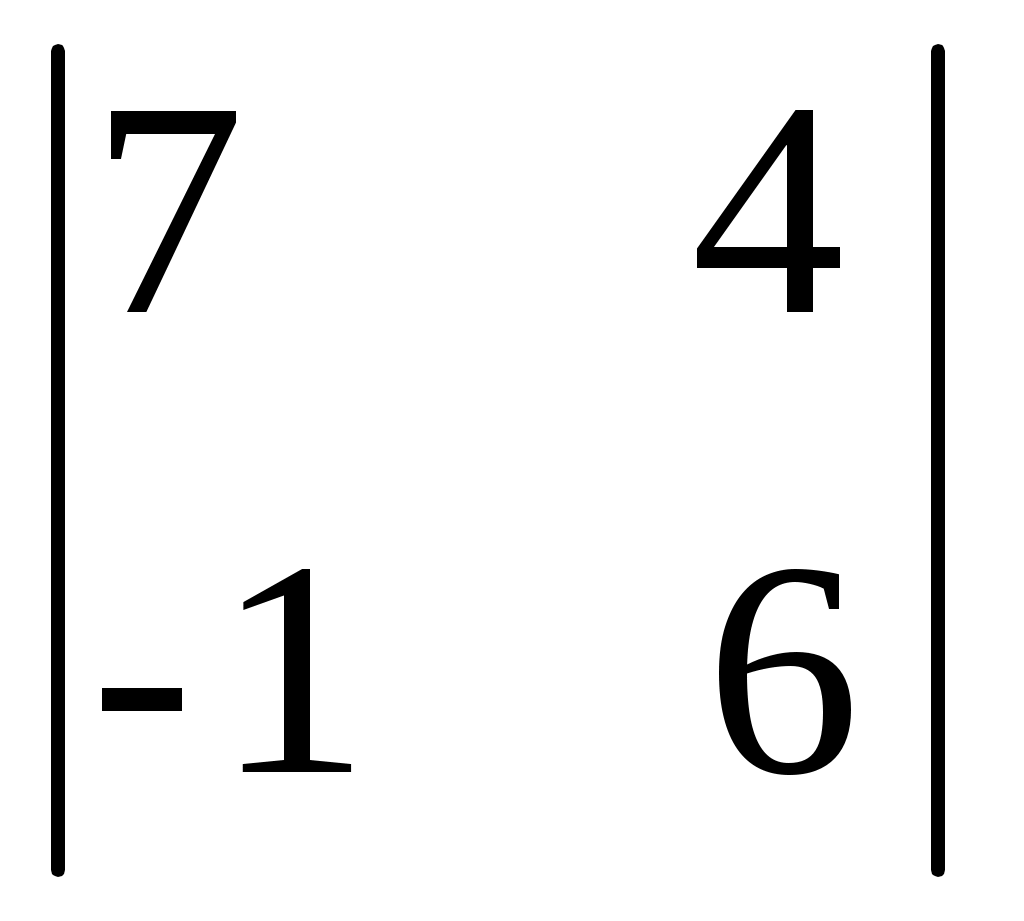 - 30 · - 30 · 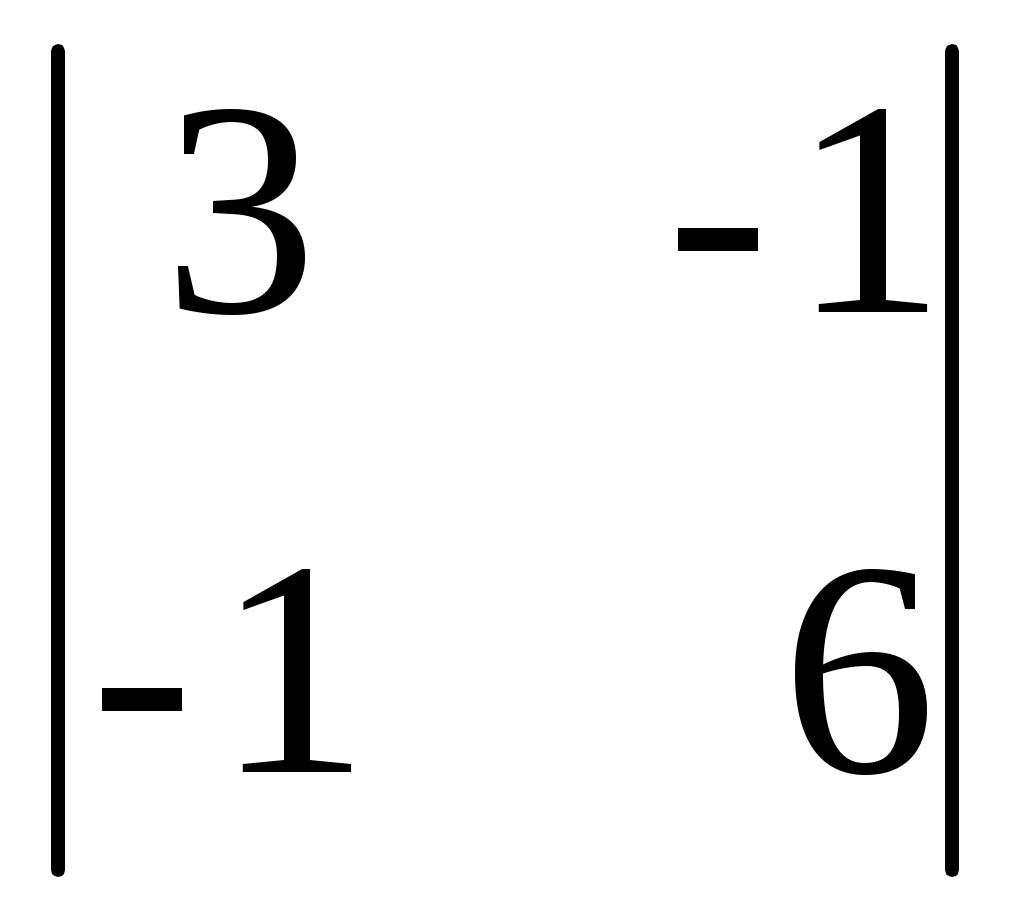 - 1 · - 1 · 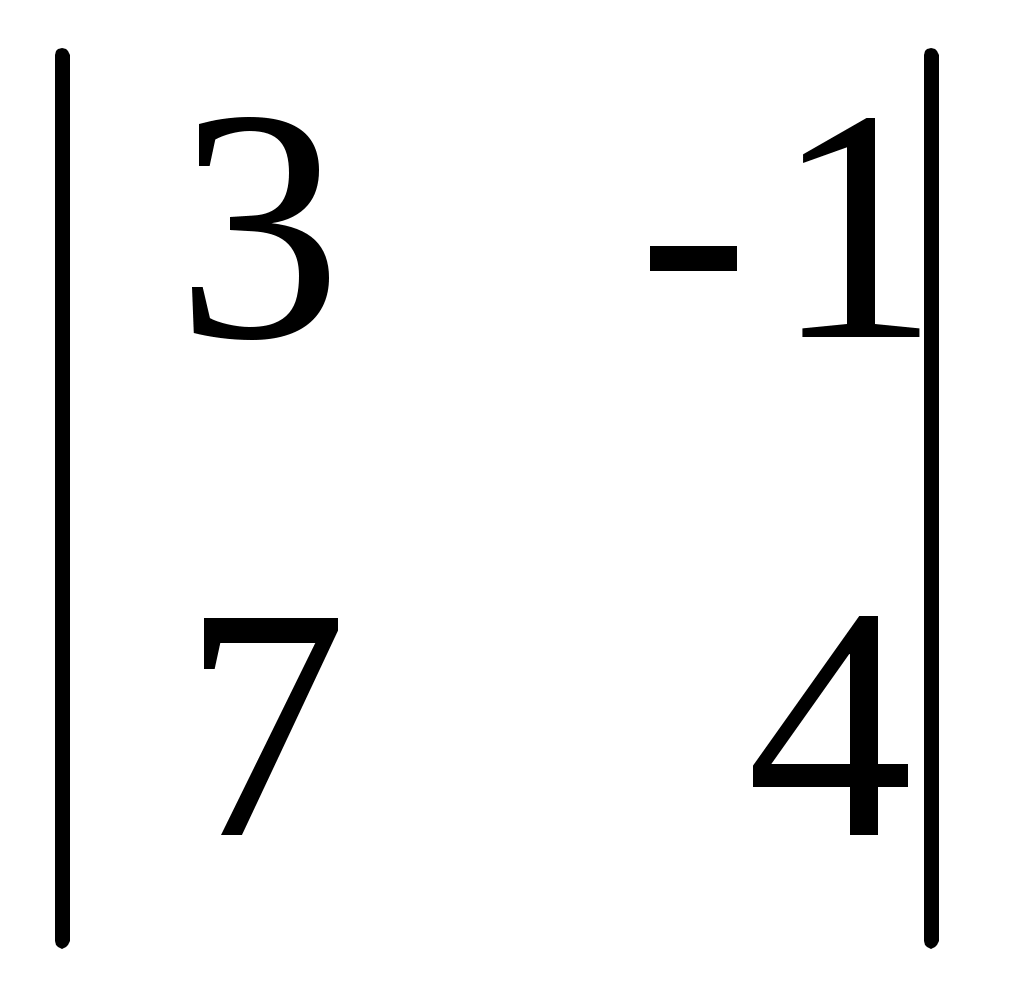 = 19·(42+4)-30·(18-1)-1·(12+7) = 19·46- = 19·(42+4)-30·(18-1)-1·(12+7) = 19·46-
30·17-19 = 345
D2 = 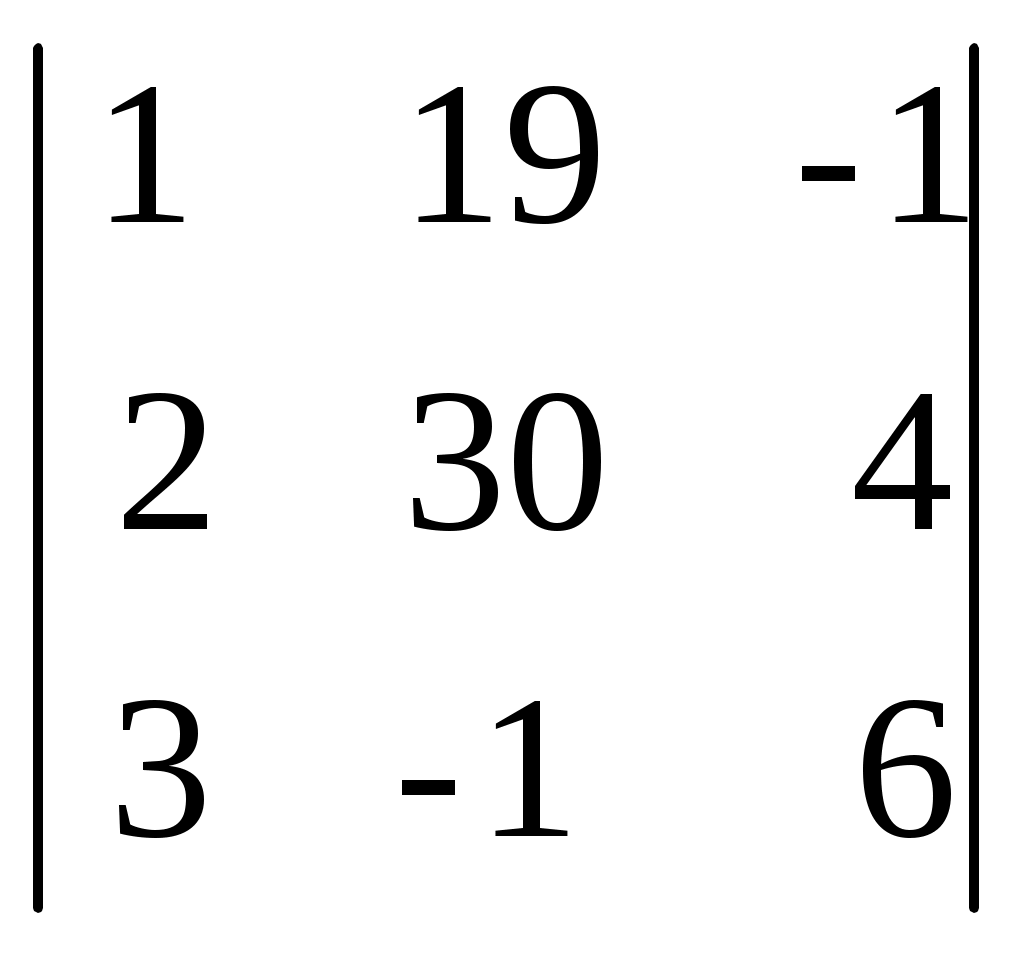 = (разложим по второму столбцу) = -19 · = (разложим по второму столбцу) = -19 ·  +30 · +30 · 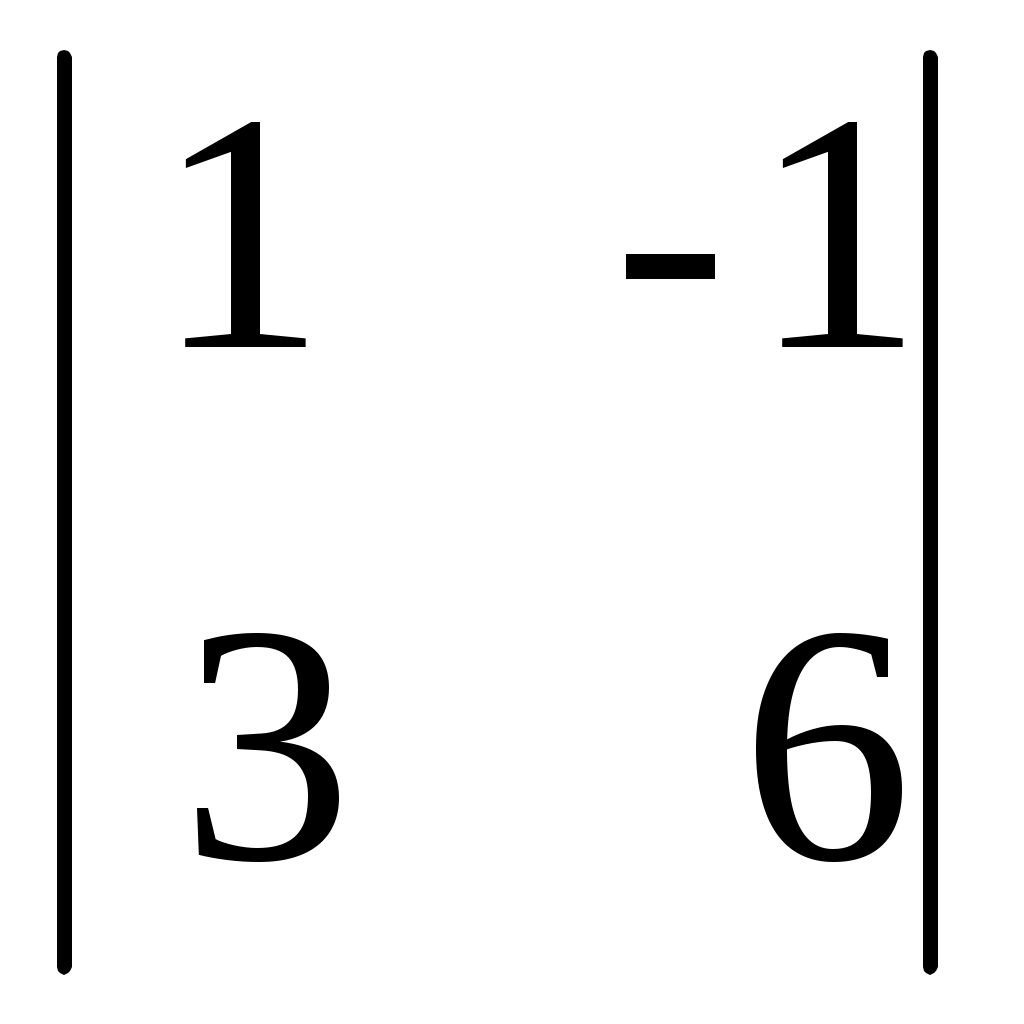
+1· 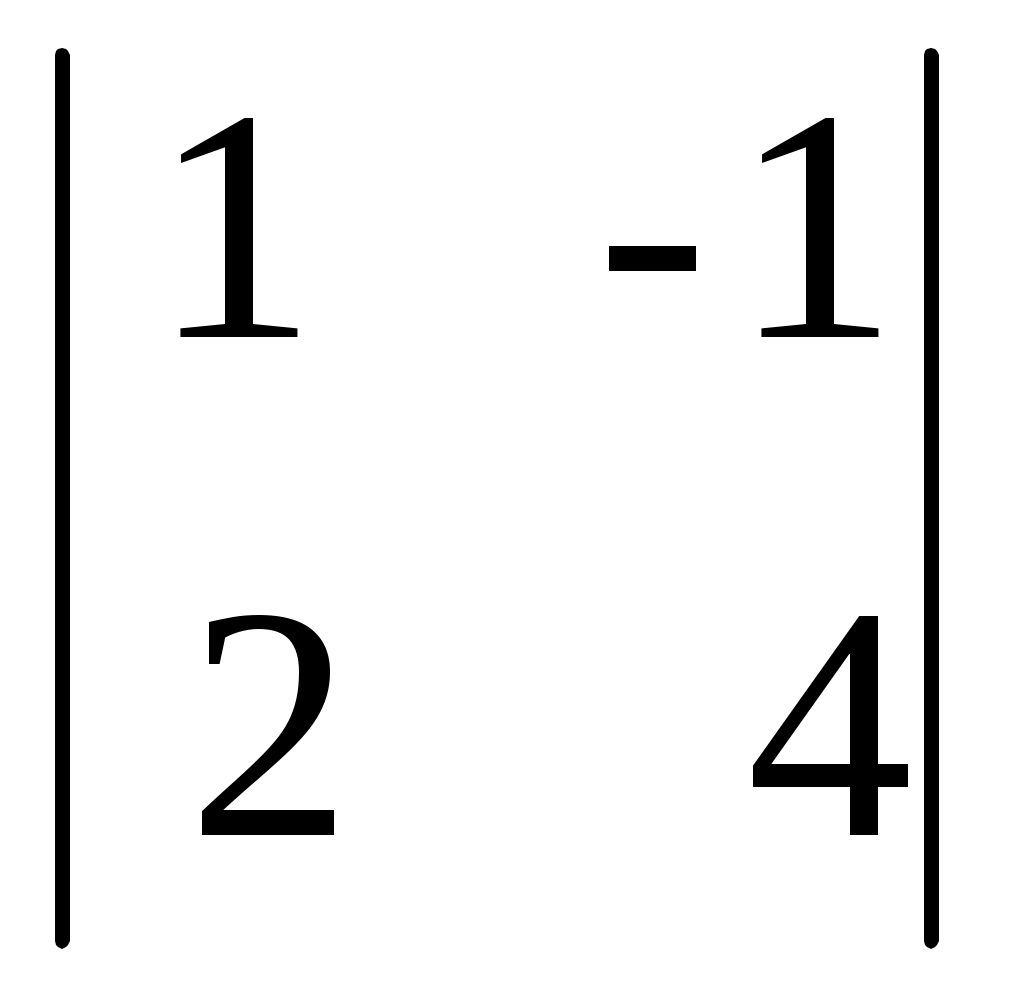 = -19·(12-12)+30·(6+3)+(4+2) = 30·9+6 = 276 = -19·(12-12)+30·(6+3)+(4+2) = 30·9+6 = 276
D3=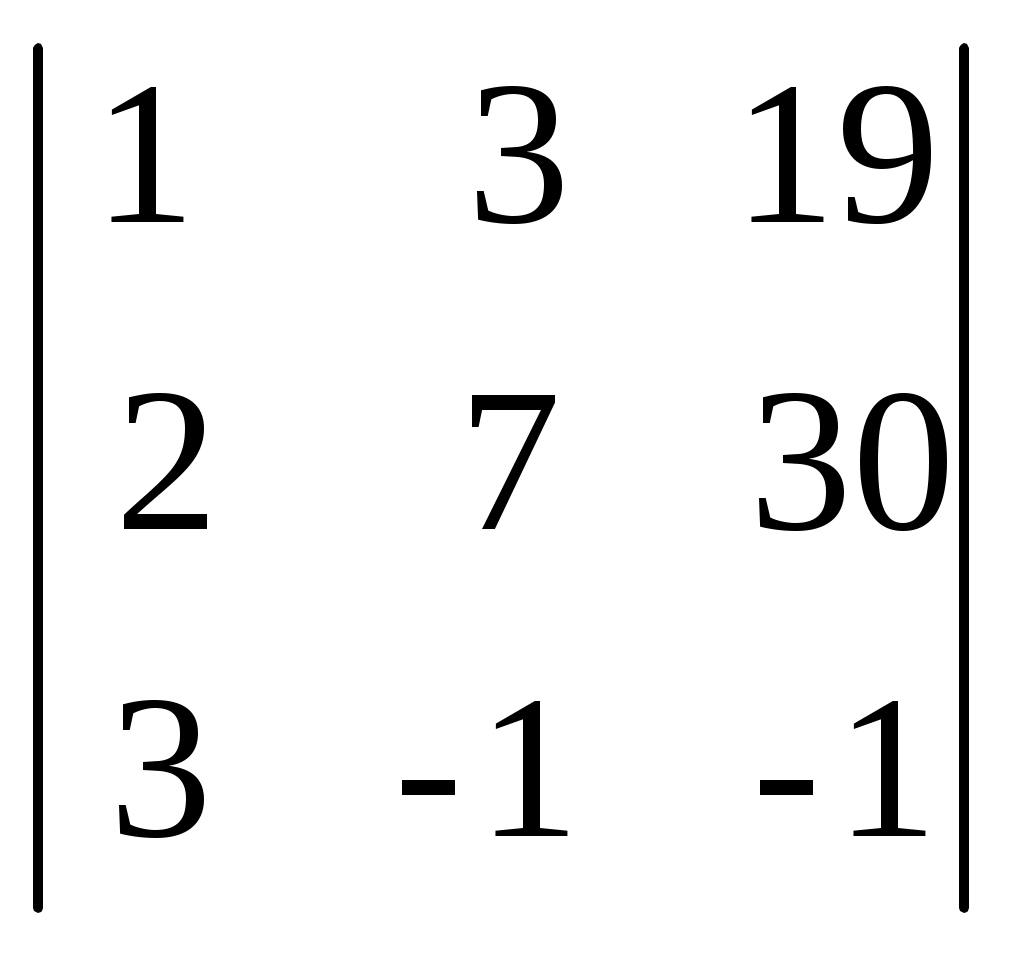 = (разложим по третьему столбцу) = 19 · = (разложим по третьему столбцу) = 19 · 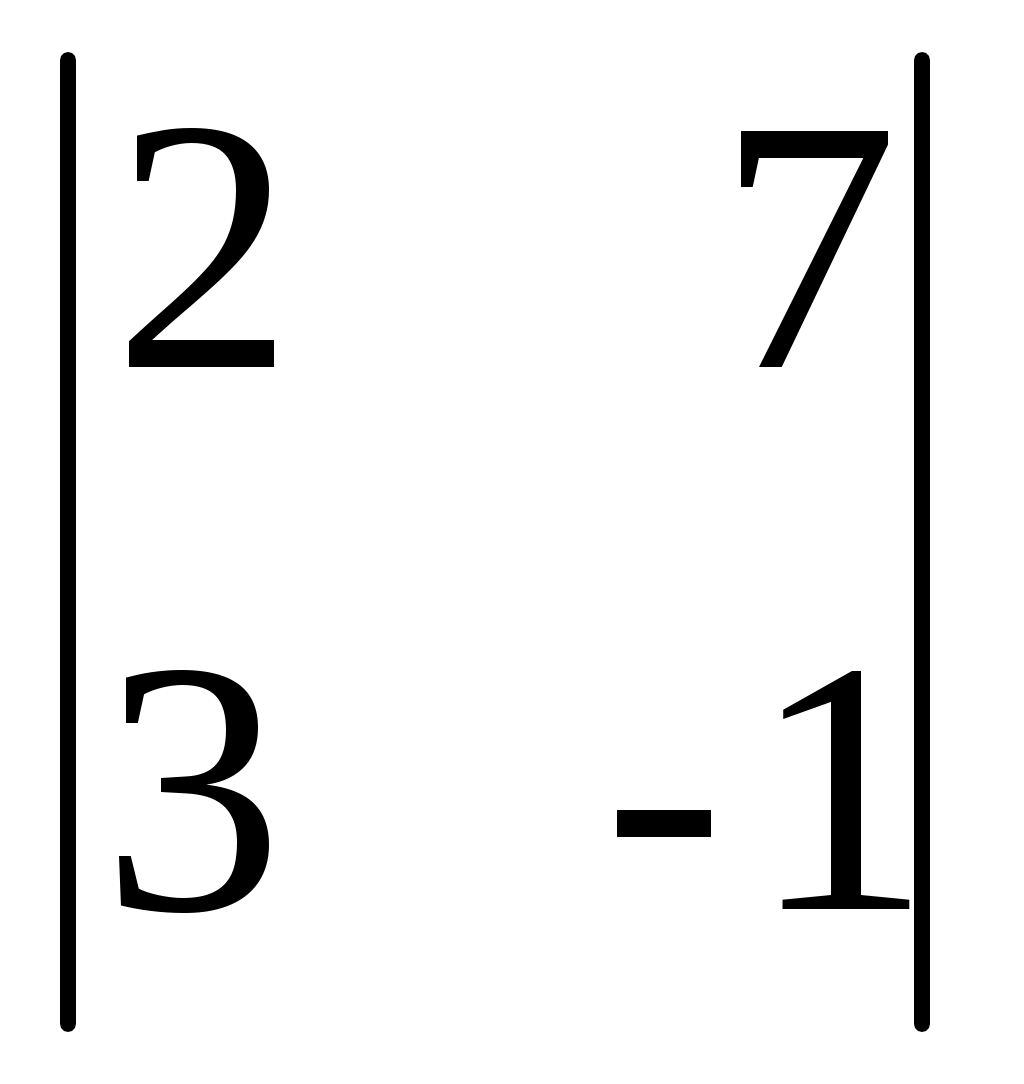 - 30 · - 30 · 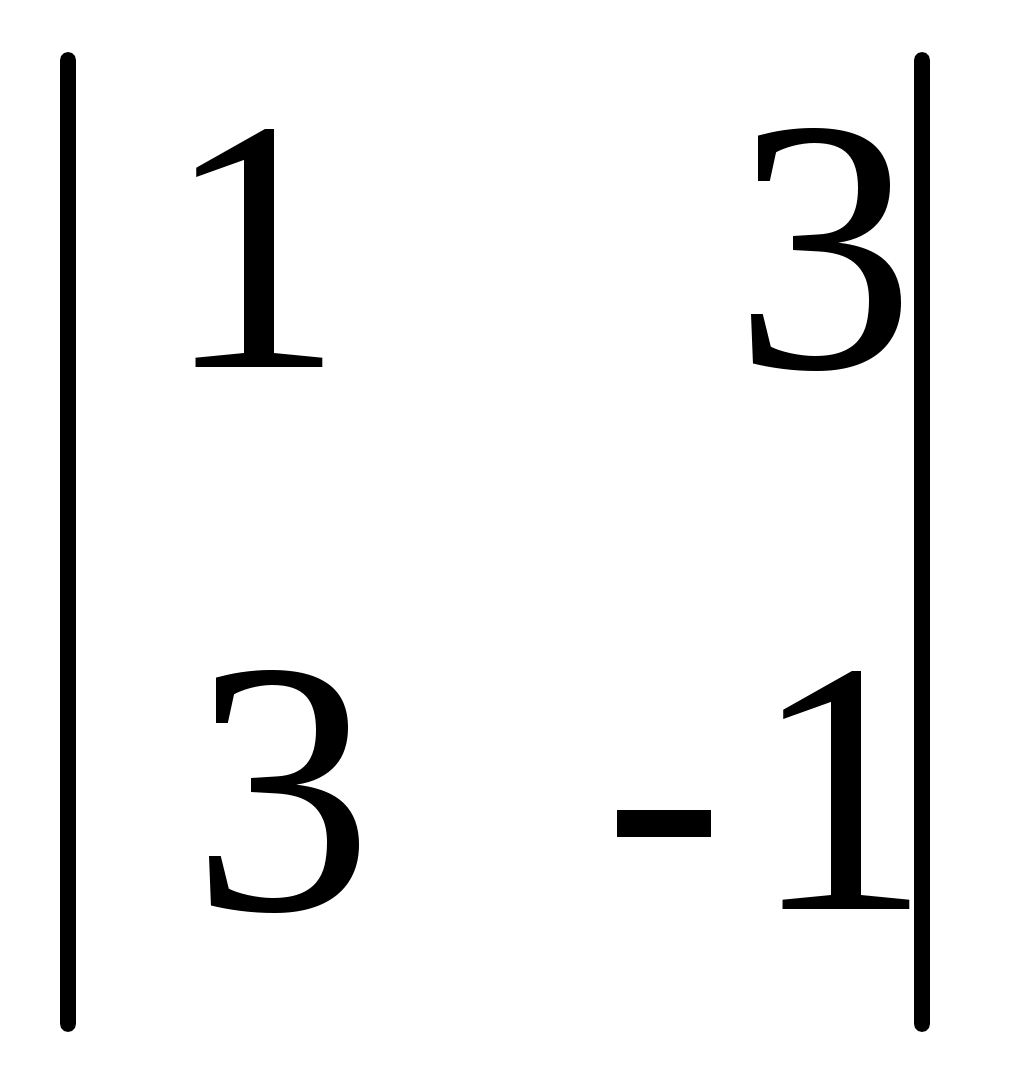 - -
1 · 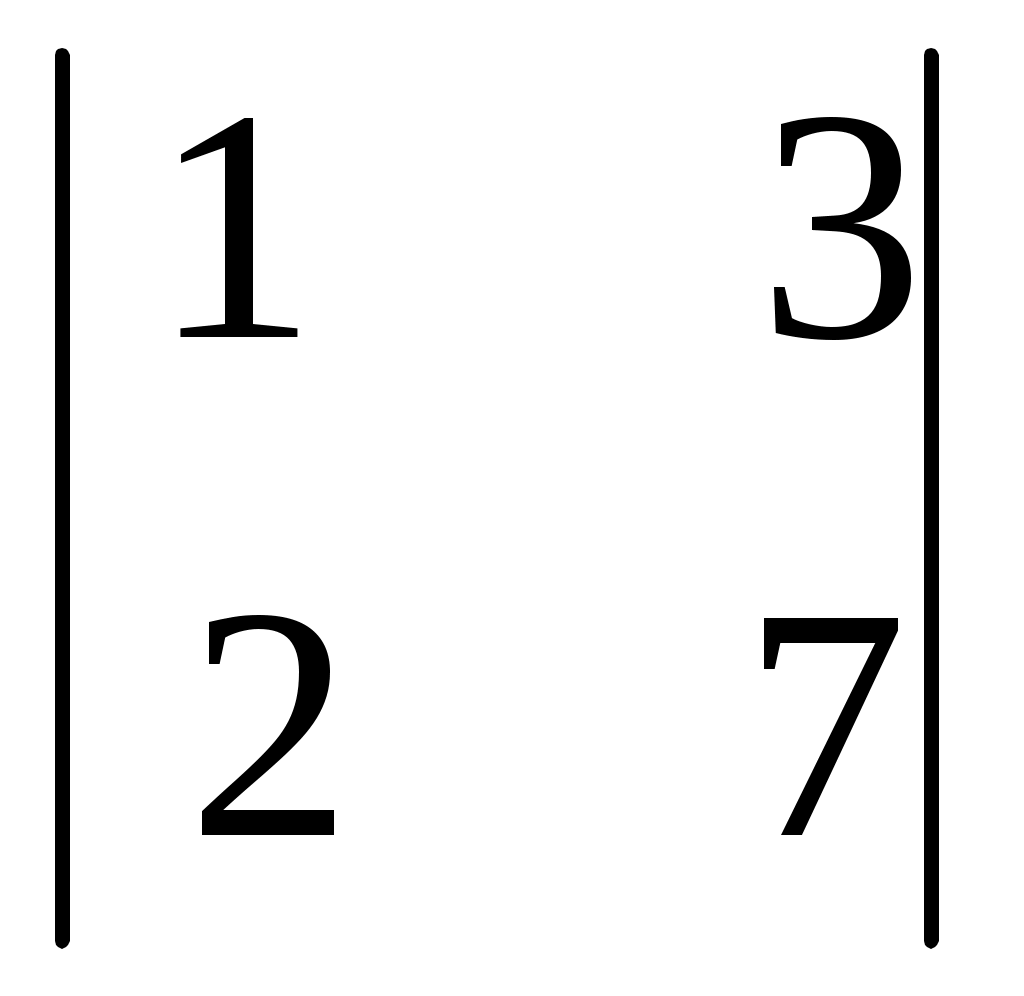 = 19·(-23)-30·(-10)-1·1 = -138 = 19·(-23)-30·(-10)-1·1 = -138
х1=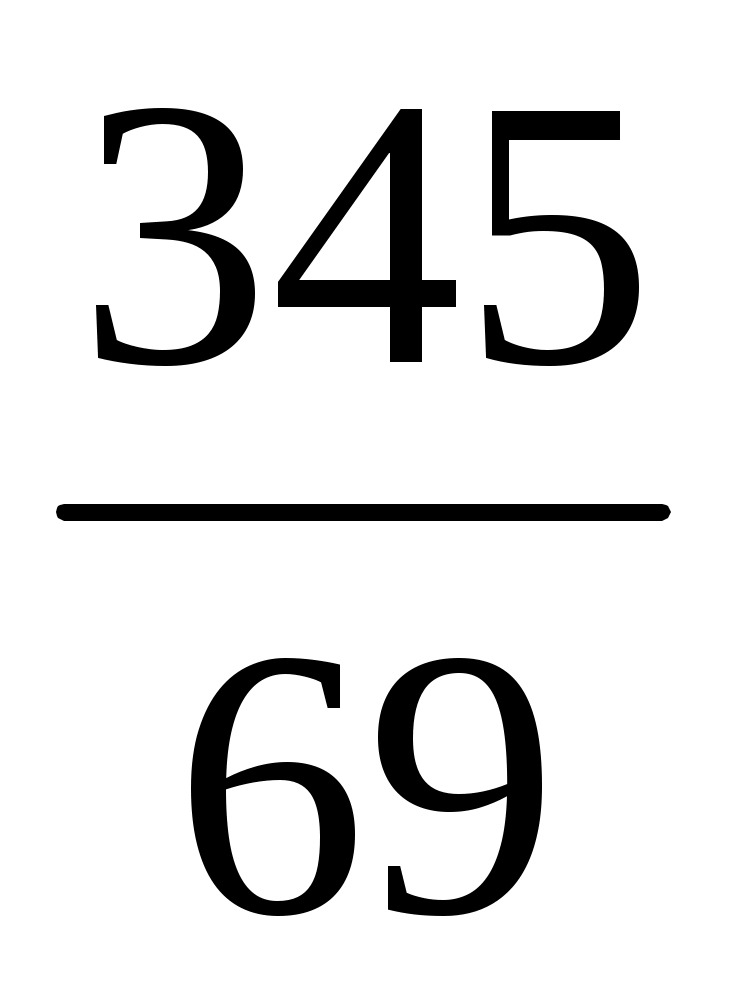 =5; х2= =5; х2=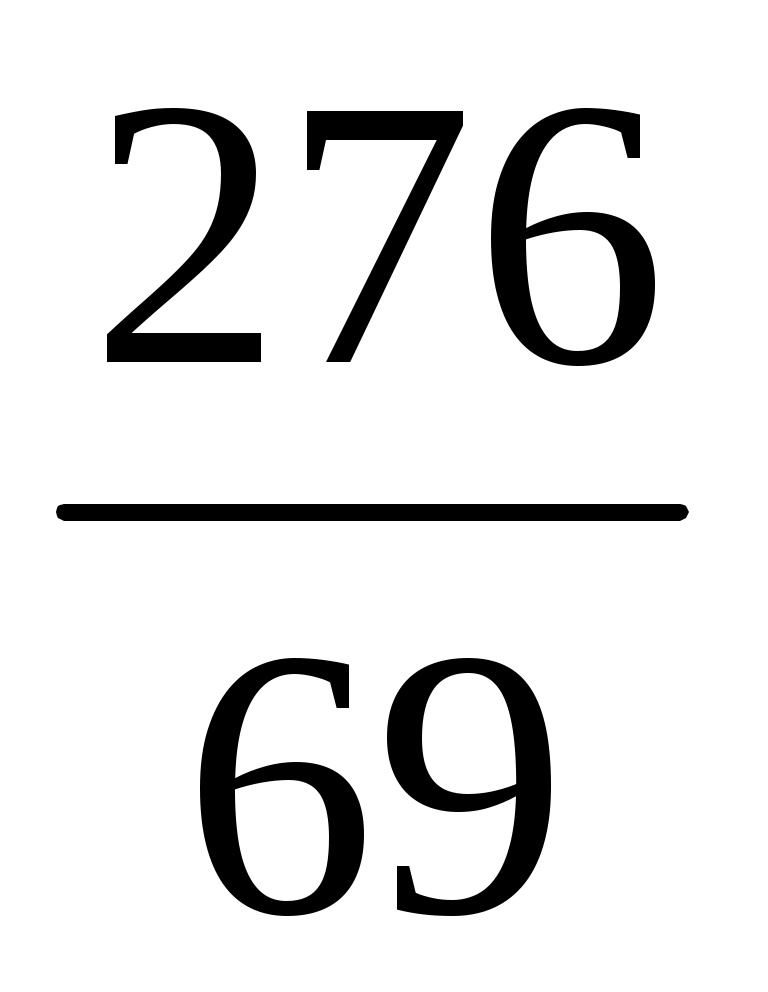 =4; х3= =4; х3=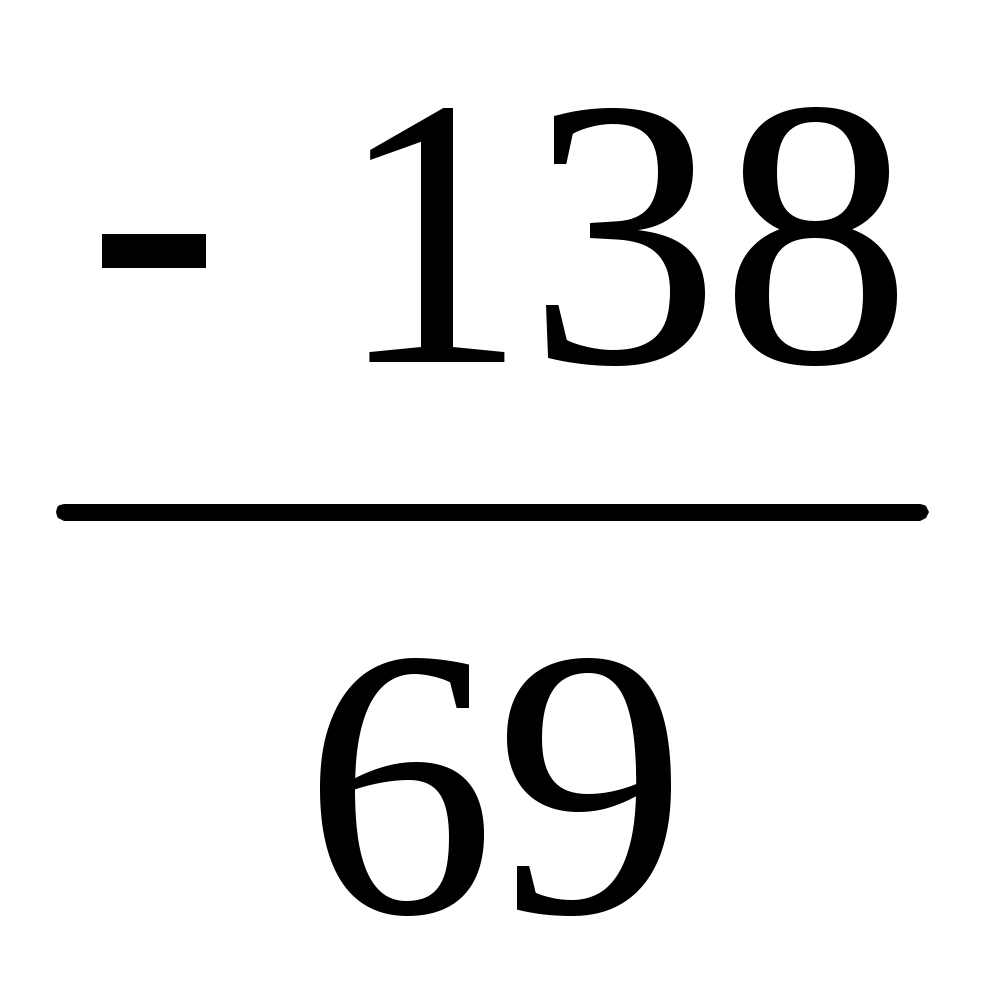 = -2 = -2
Ответ: (5; 4; -2)
3. Метод Гаусса
Метод состоит в приведении расширенной матрицы к ступенчатому виду с помощью элементарных преобразований. Этот метод называют методом последовательного исключения неизвестных.
Пример: Решите систему методом Гаусса
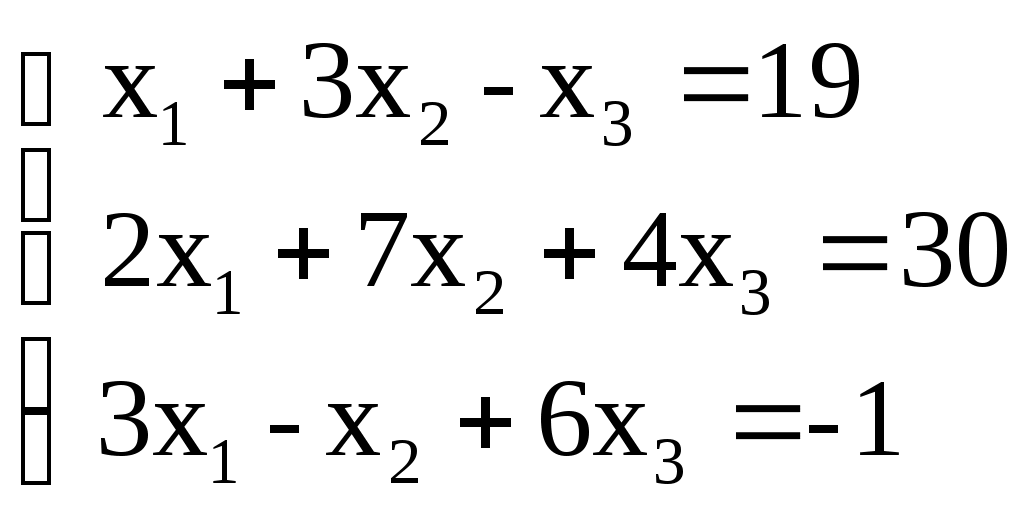
Составим расширенную матрицу системы и приведём её с помощью равносильных преобразований к ступенчатому виду (по главной диагонали единицы, под ними нули).
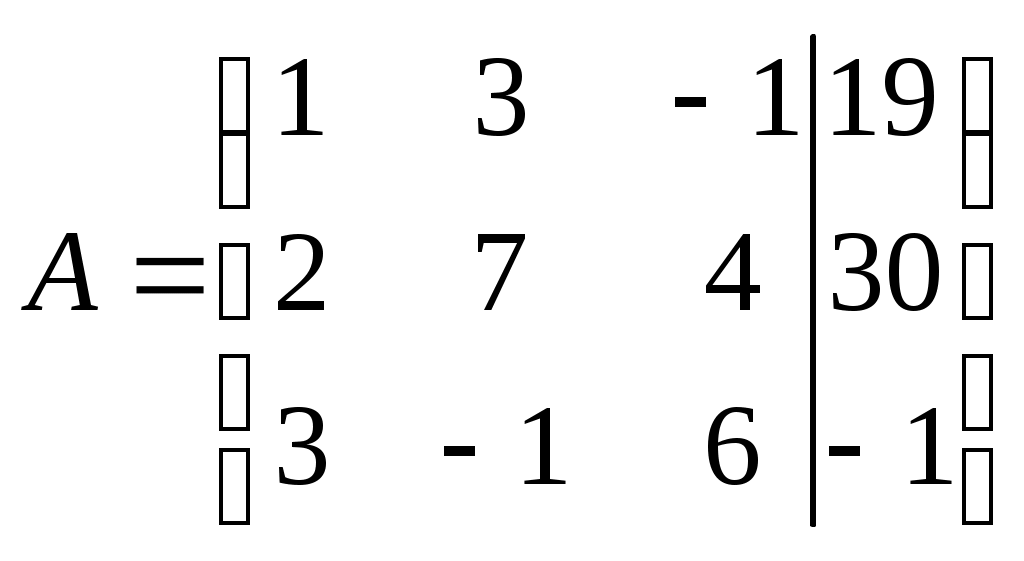
Умножим элементы первой строки на (-2) и прибавим к соответственным элементам второй строки, а так же на (-3) и прибавим к соответственным элементам третьей строки.
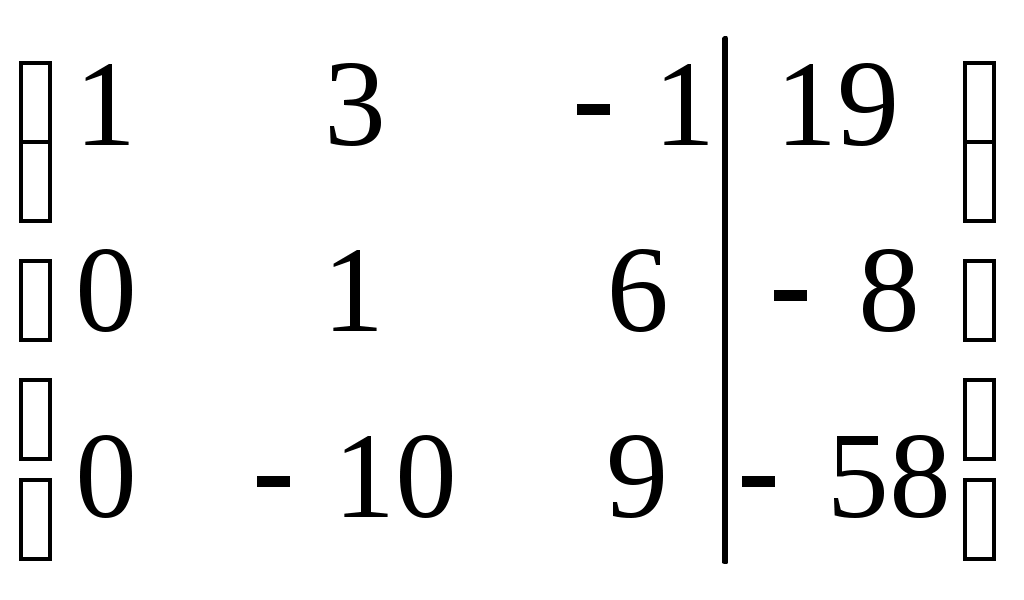
Умножим элементы второй строки на 10 и прибавим к соответственным элементам третьей строки
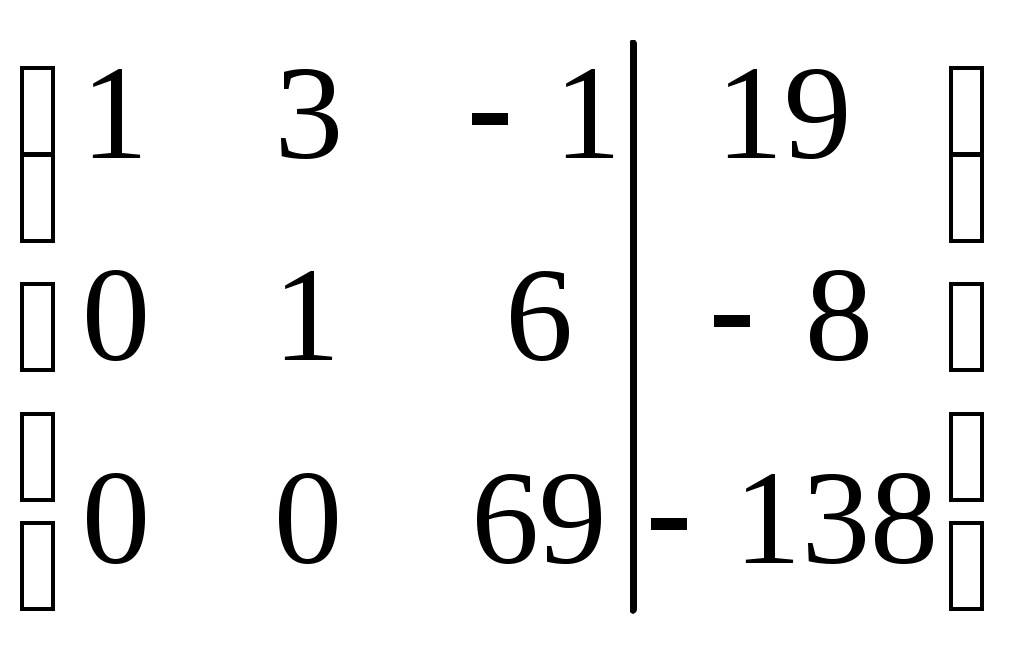
Разделим элементы третьей строки на 69
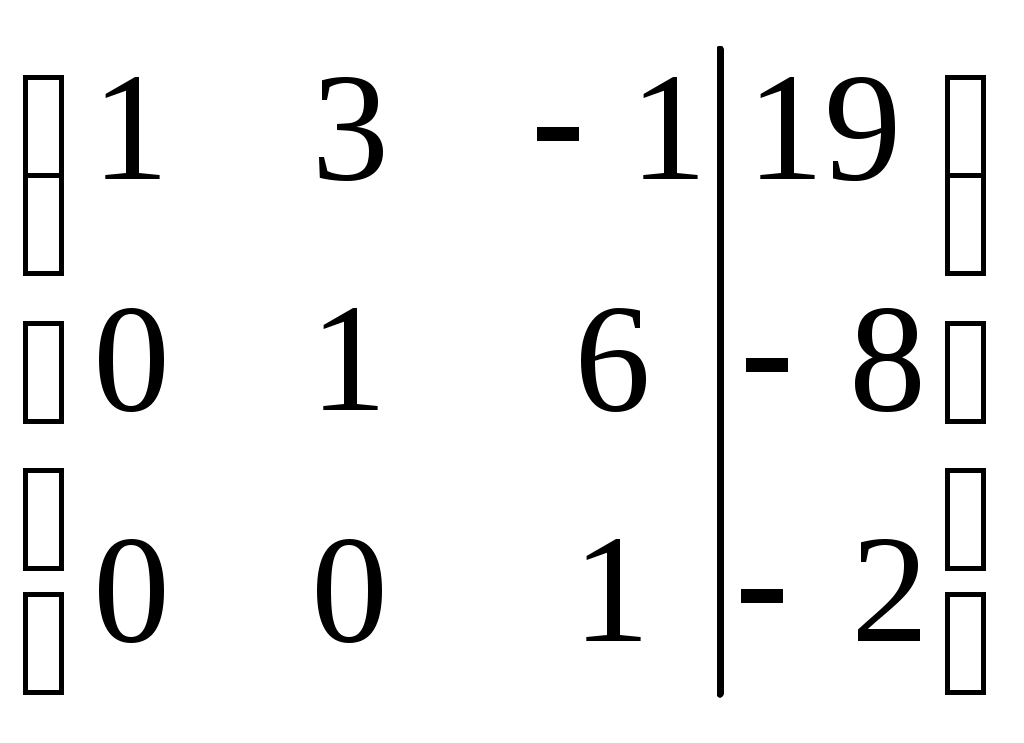
Этой матрице соответствует система, равносильная данной:
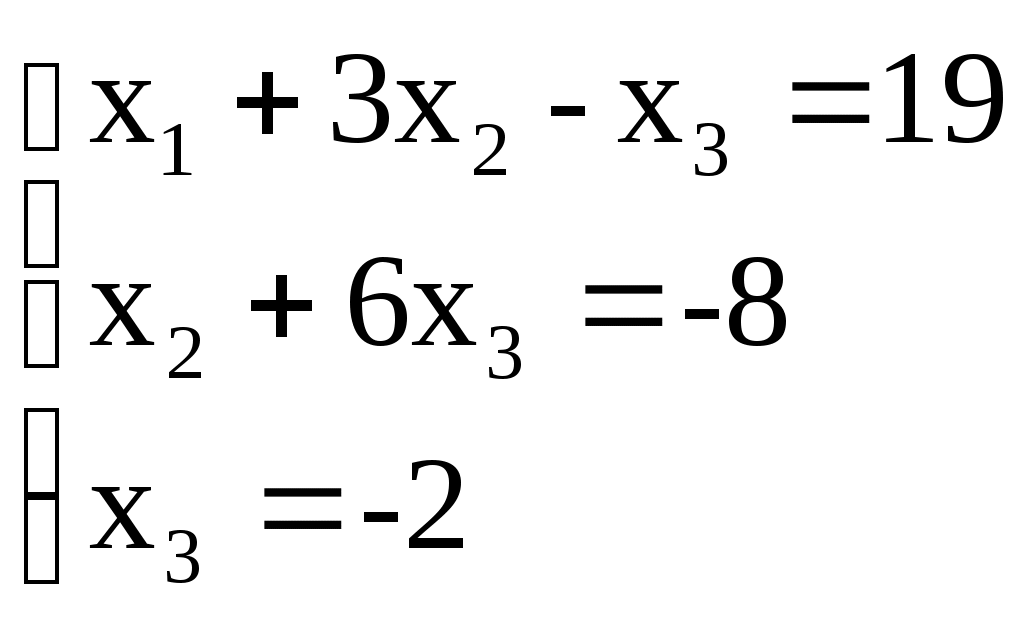 ; ; 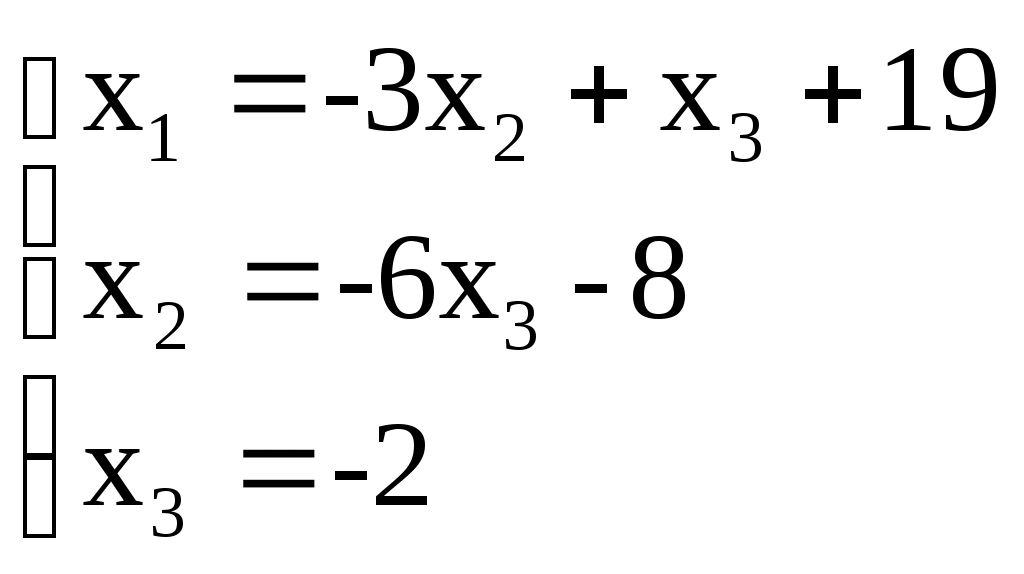 ; ; 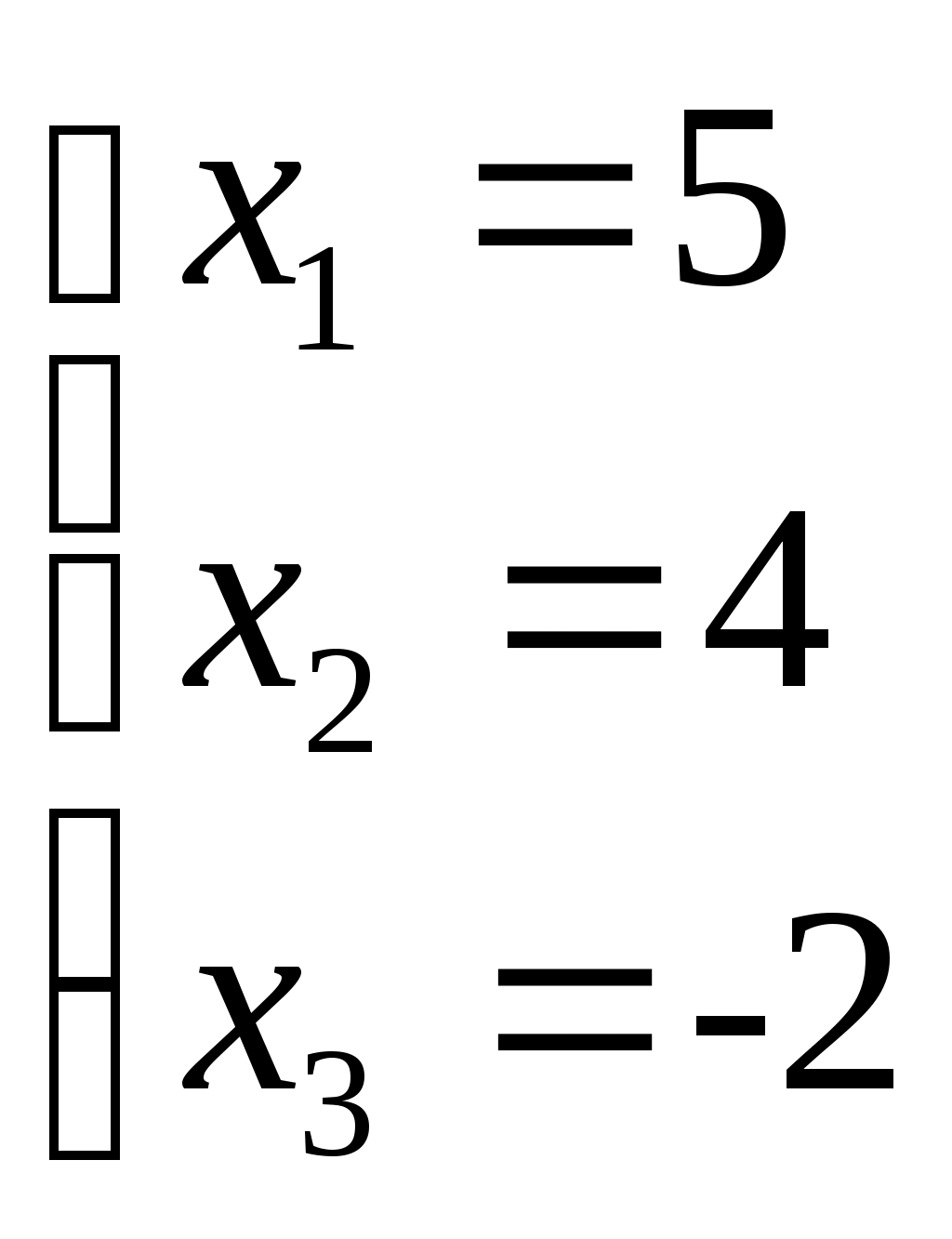
Ответ: (5; 4; -2)
|
|
|
 Скачать 262.5 Kb.
Скачать 262.5 Kb.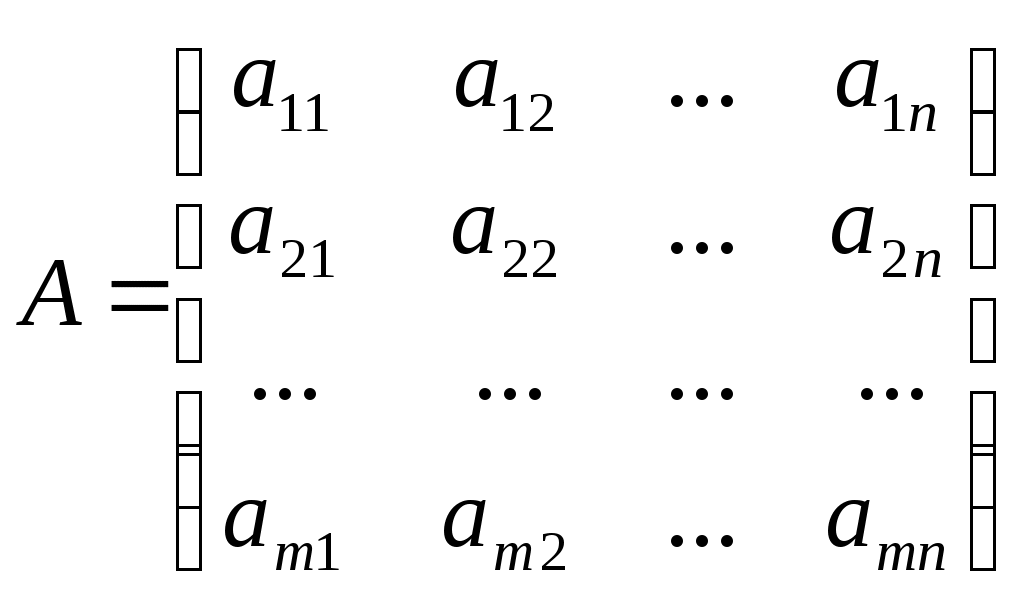
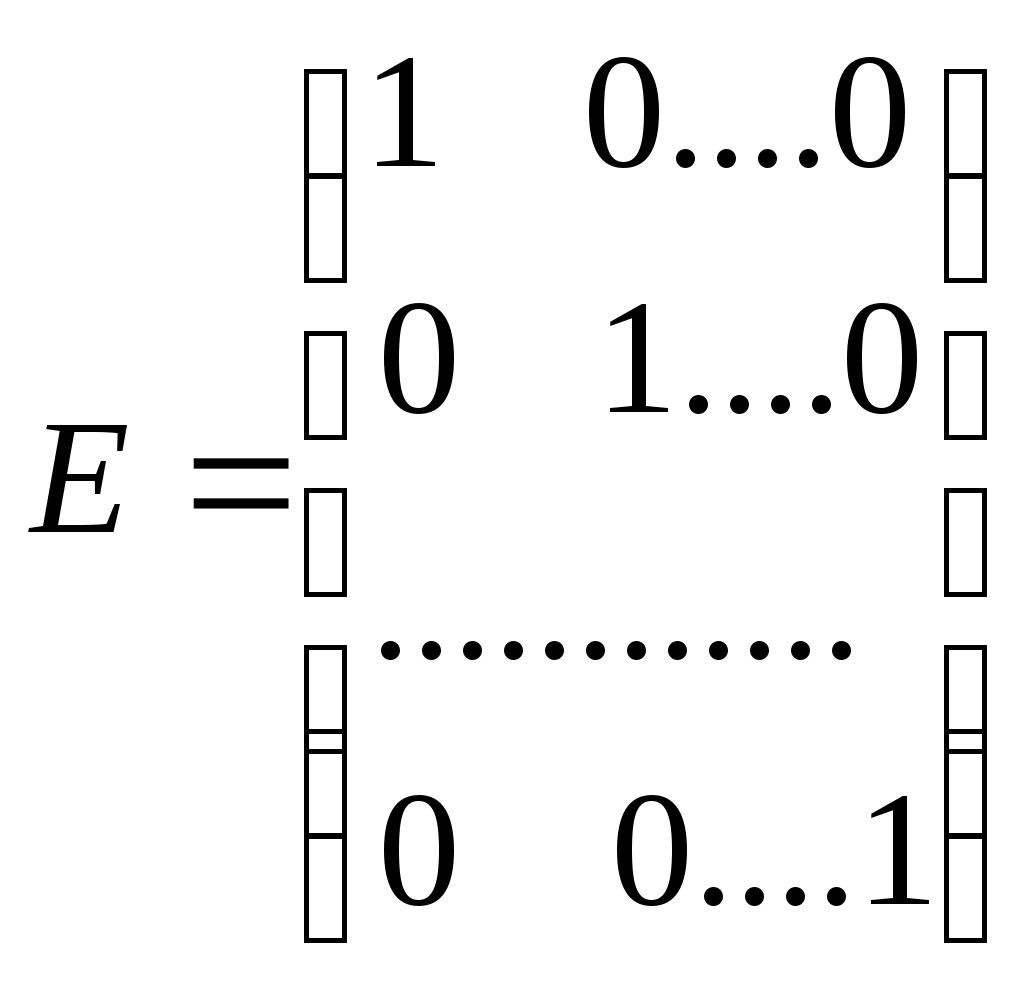


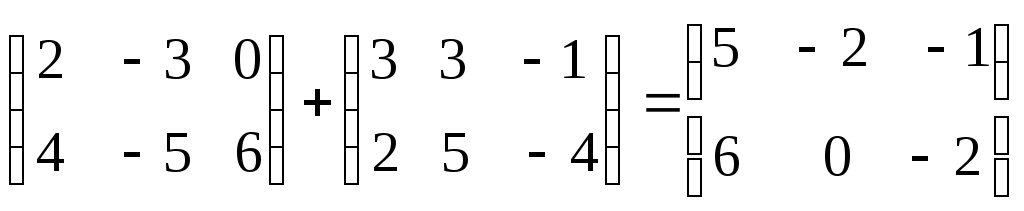
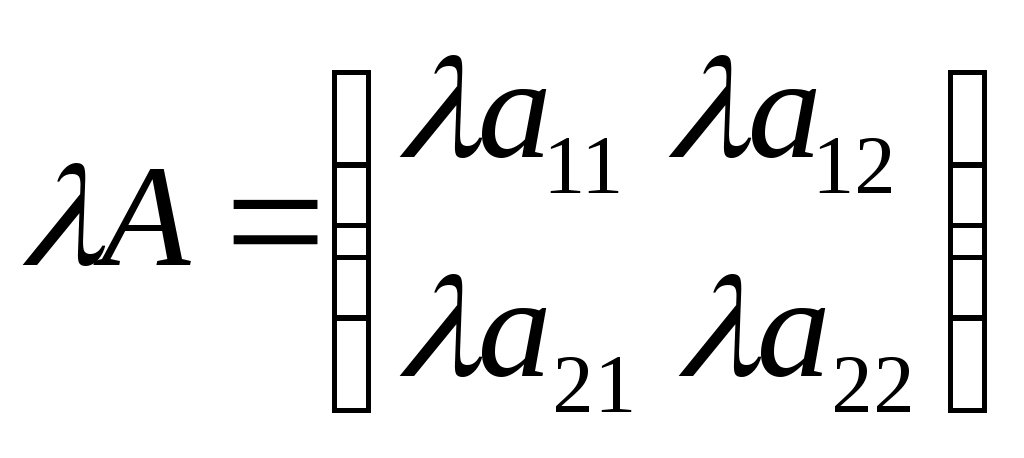 ри умножении матрицы на число, умножаются все элементы данной матрицы.
ри умножении матрицы на число, умножаются все элементы данной матрицы.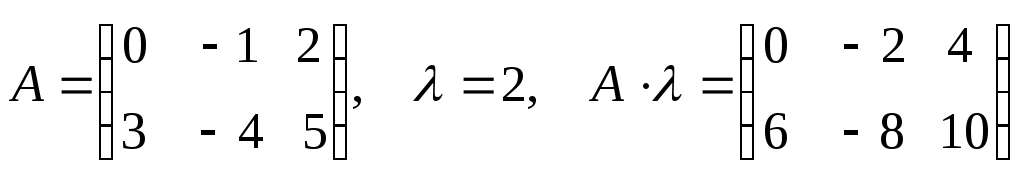
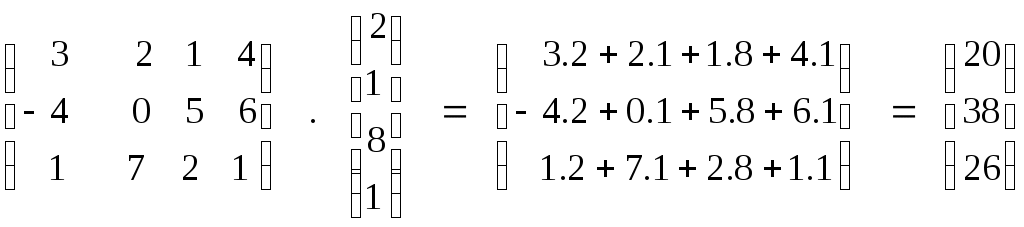
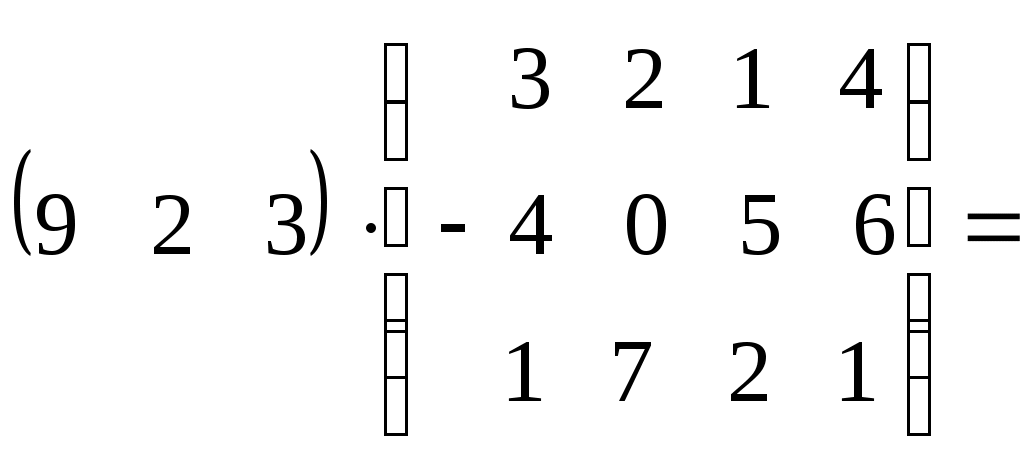
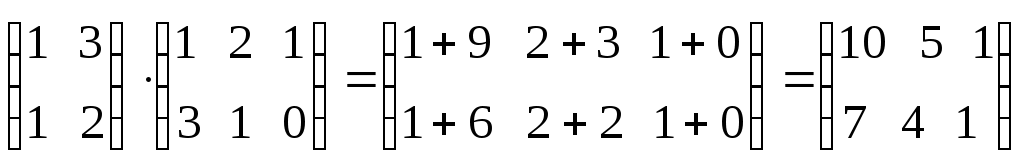
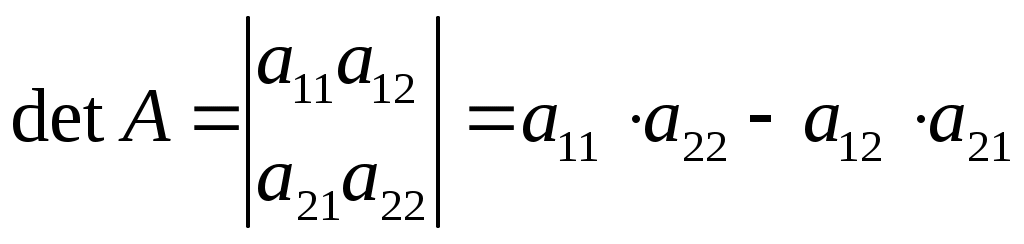




 = –
= – 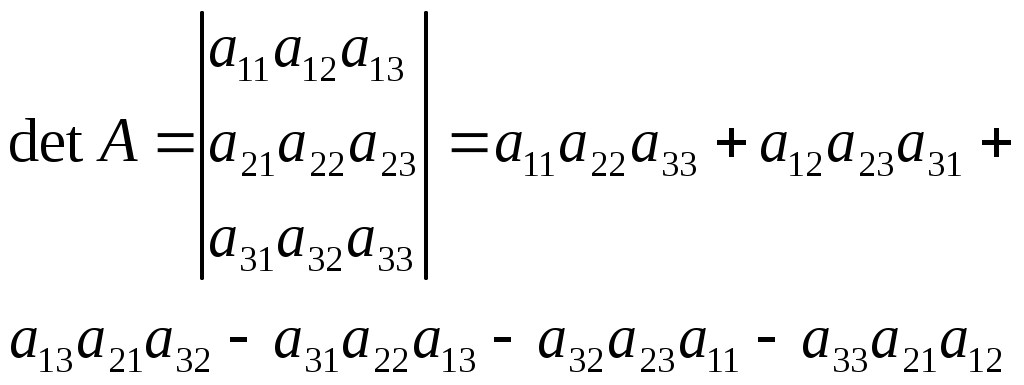





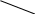
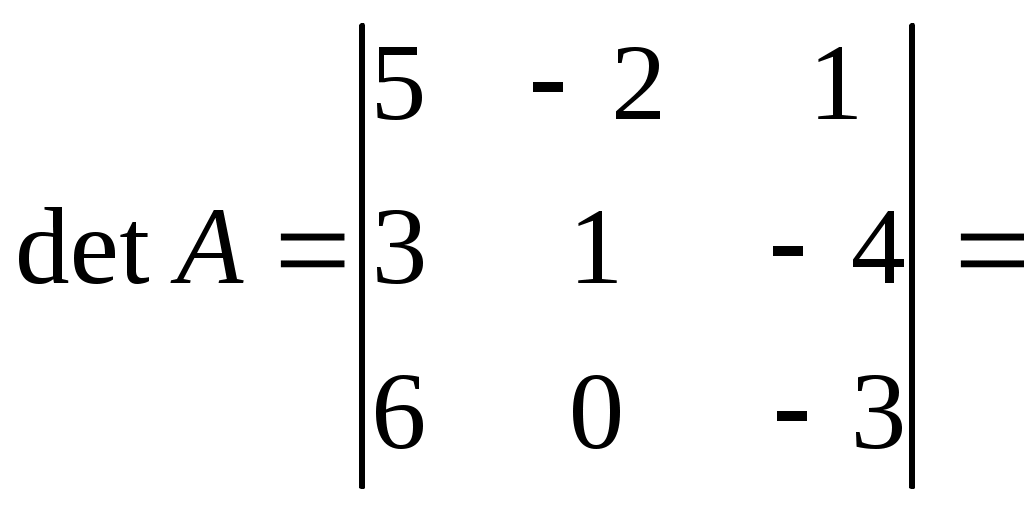
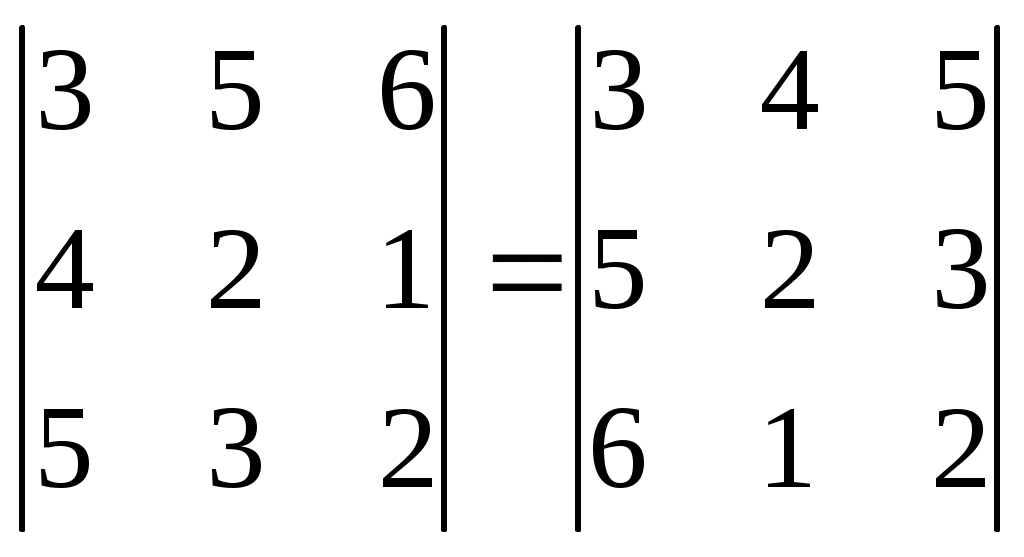
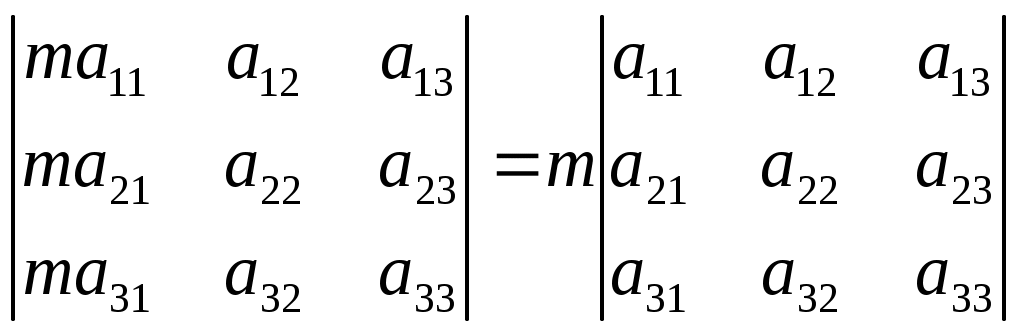

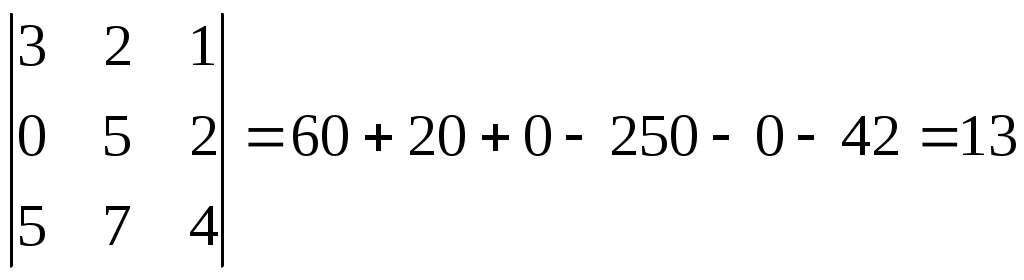

 M23=
M23=
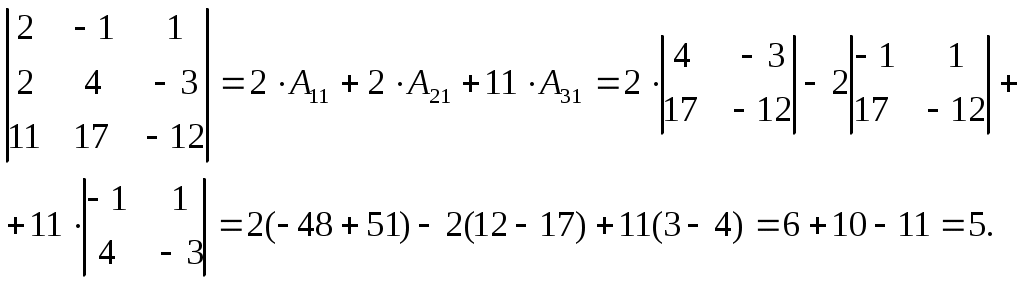
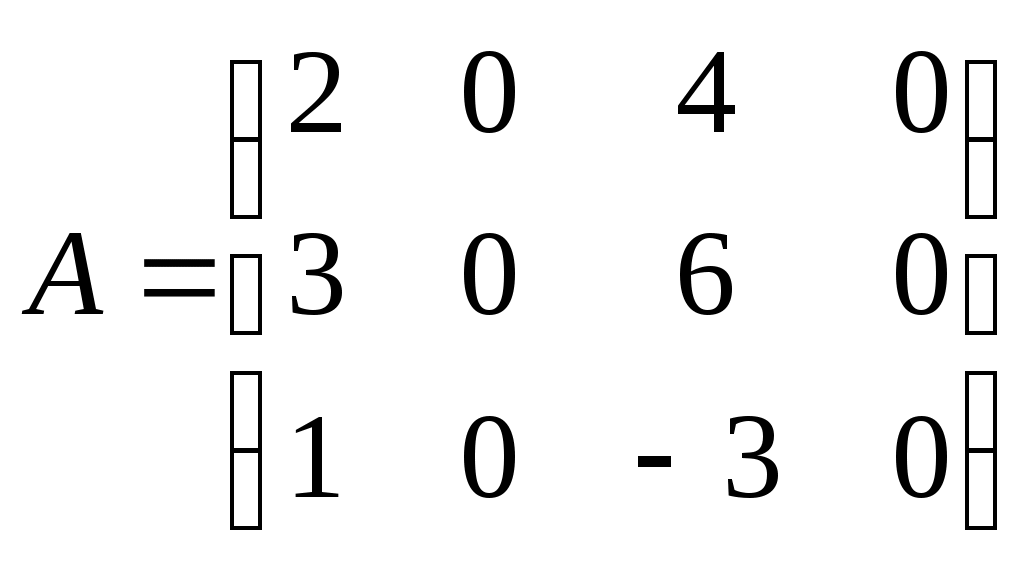
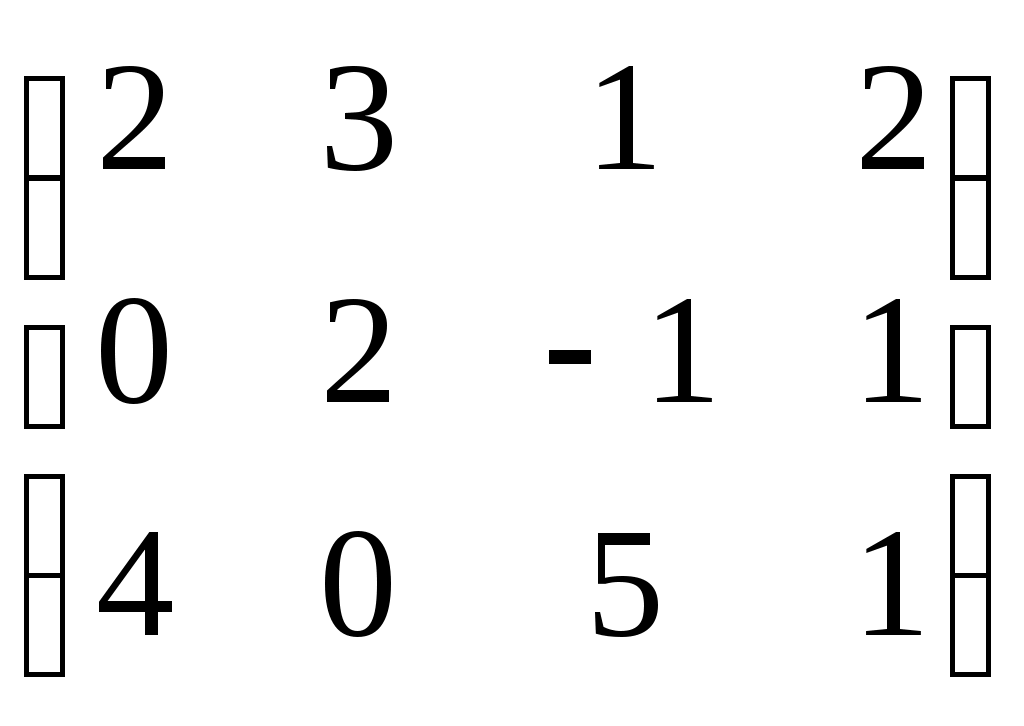
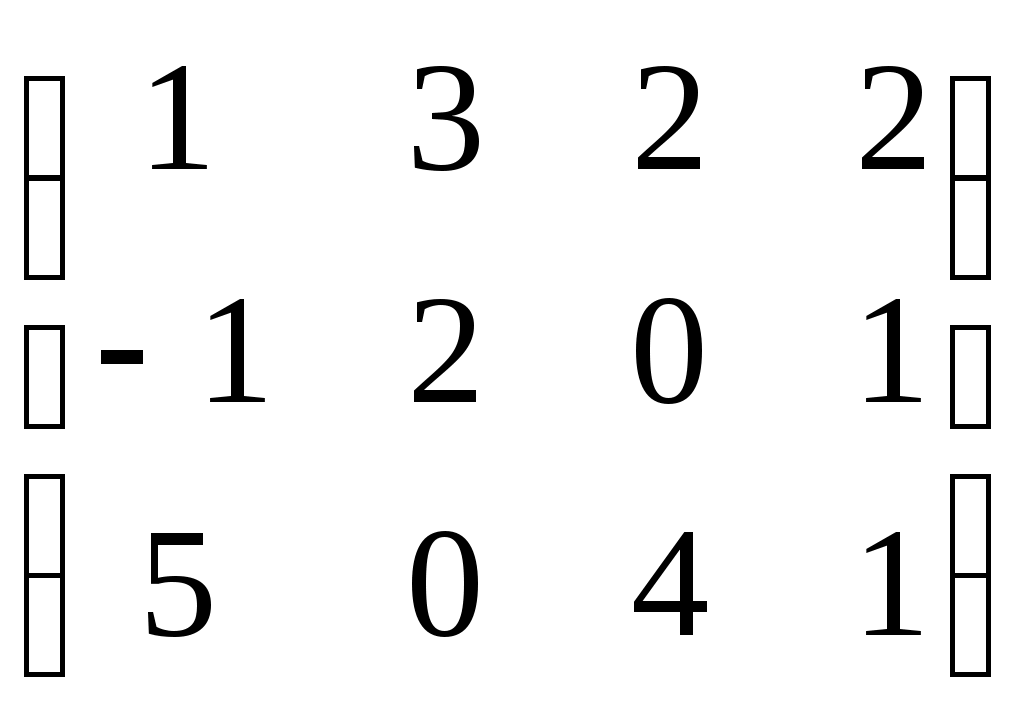
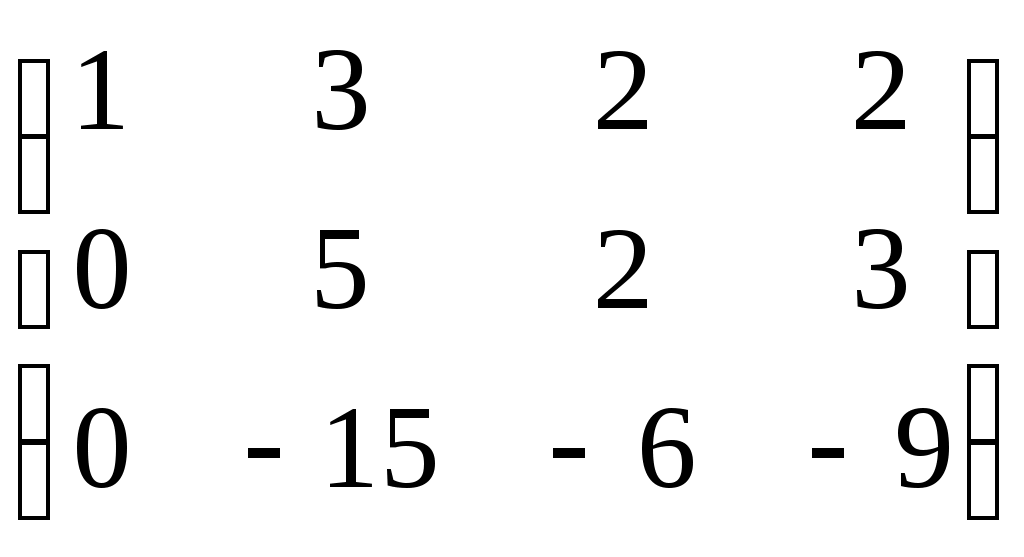
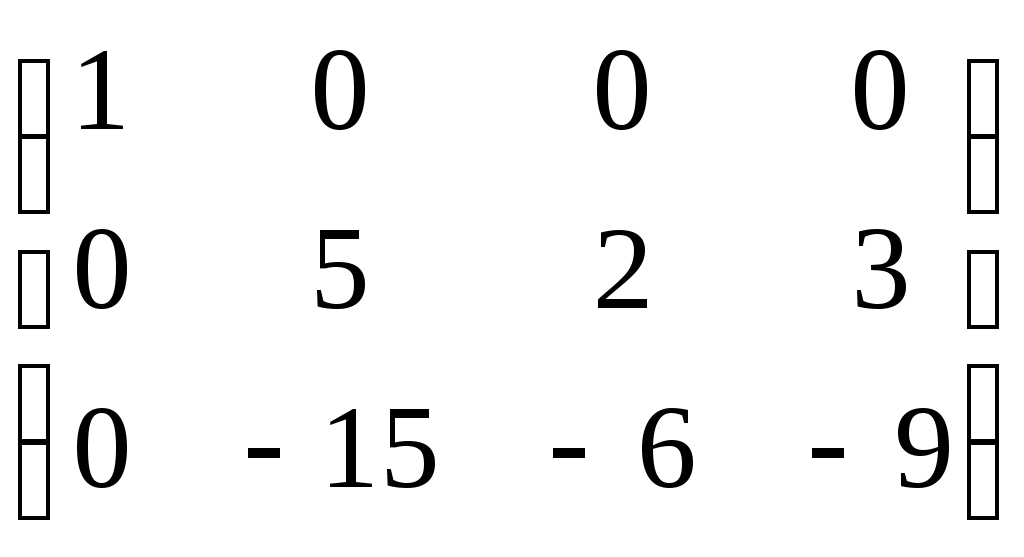
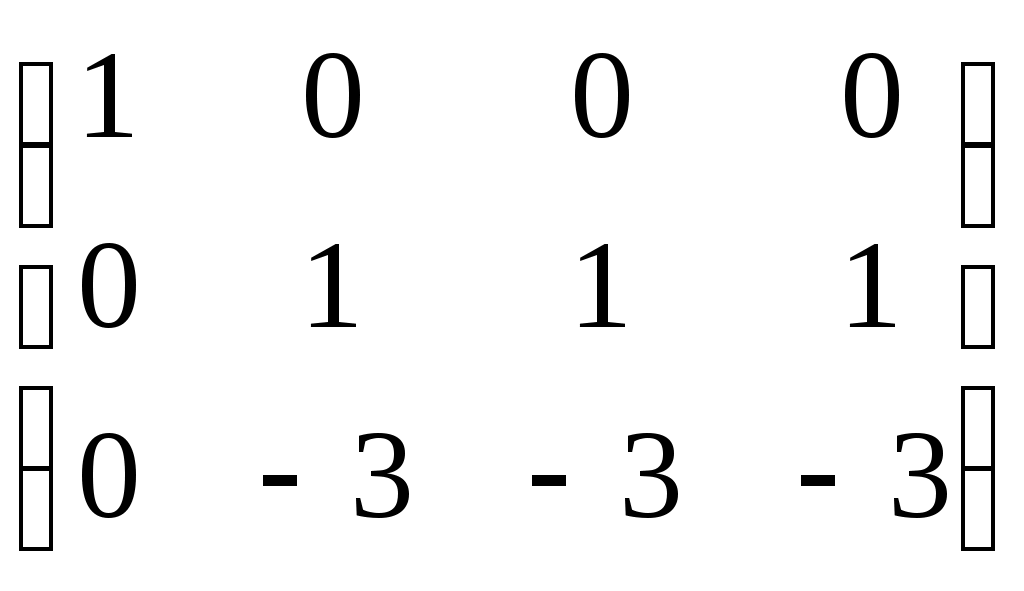
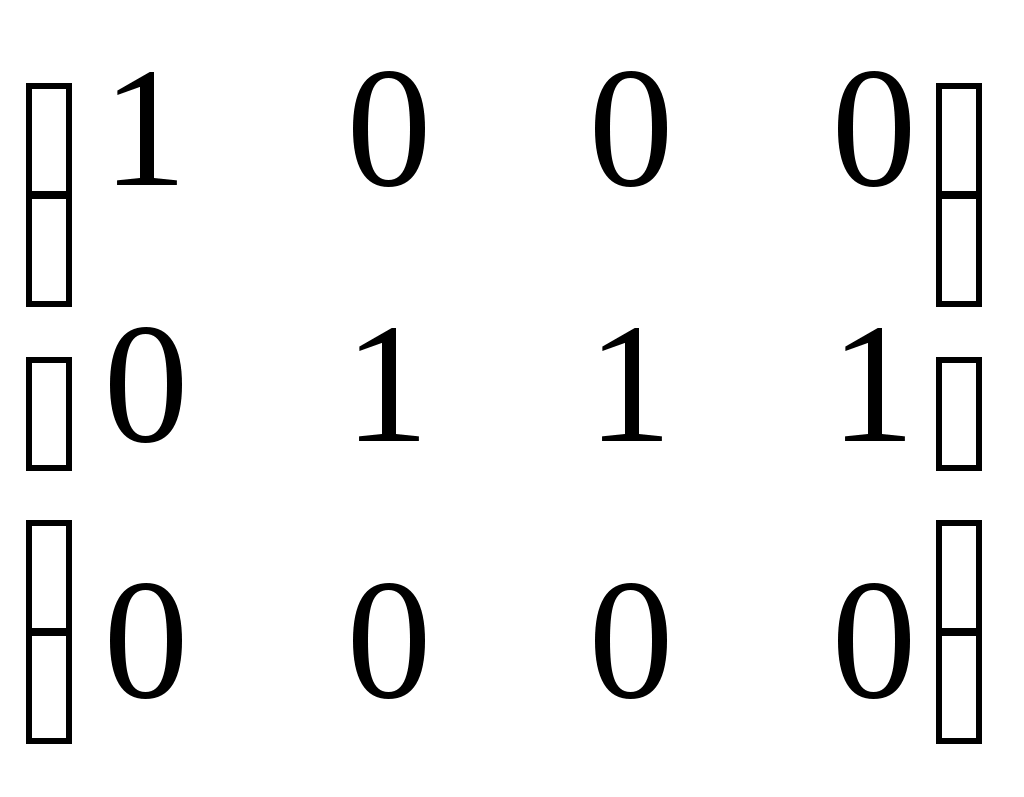
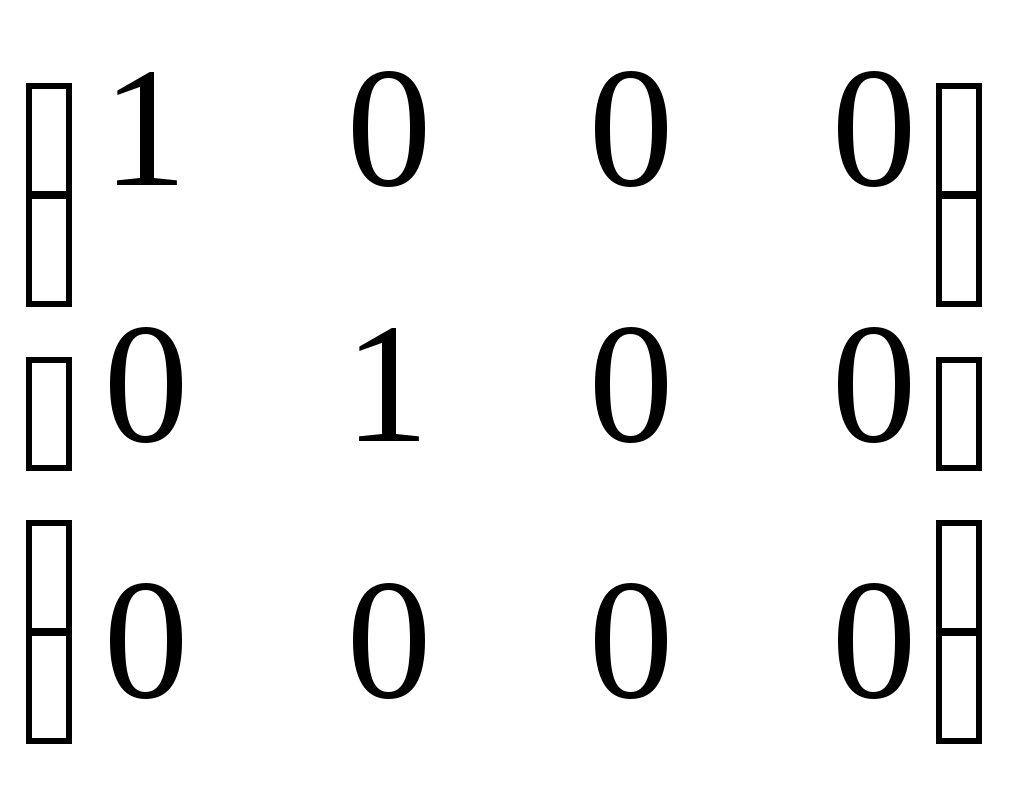 rang A=2
rang A=2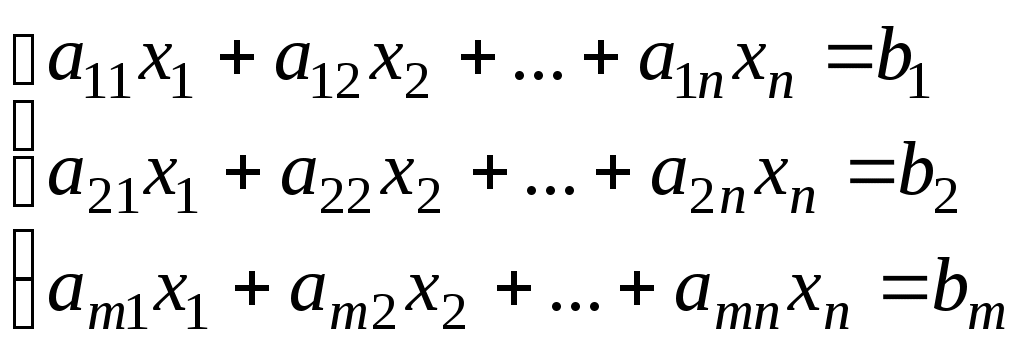 (I)
(I)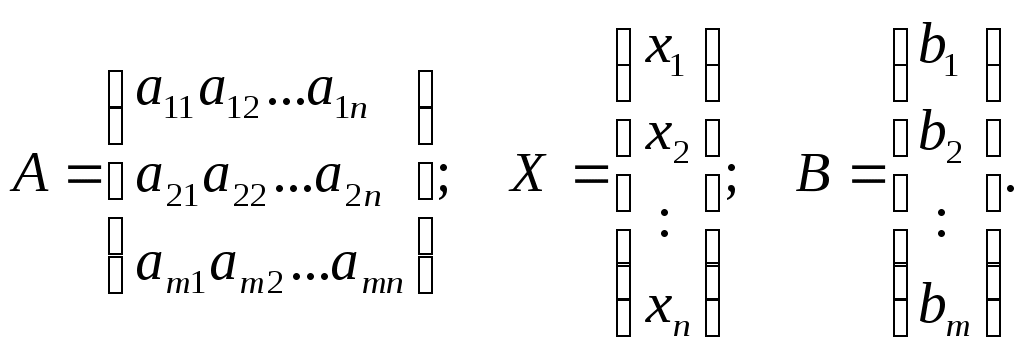
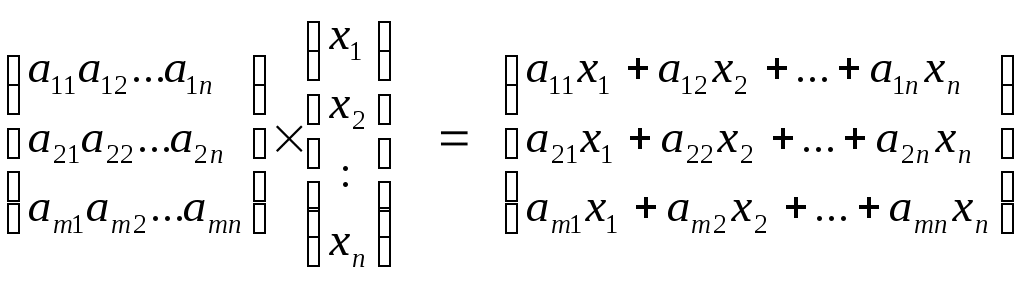
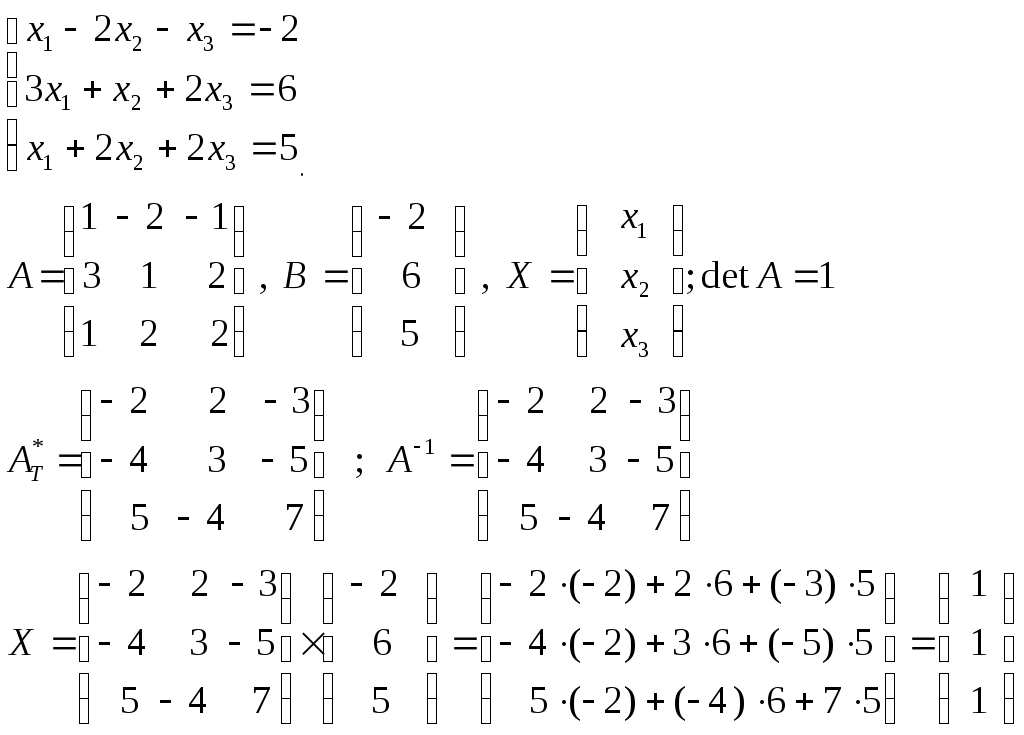
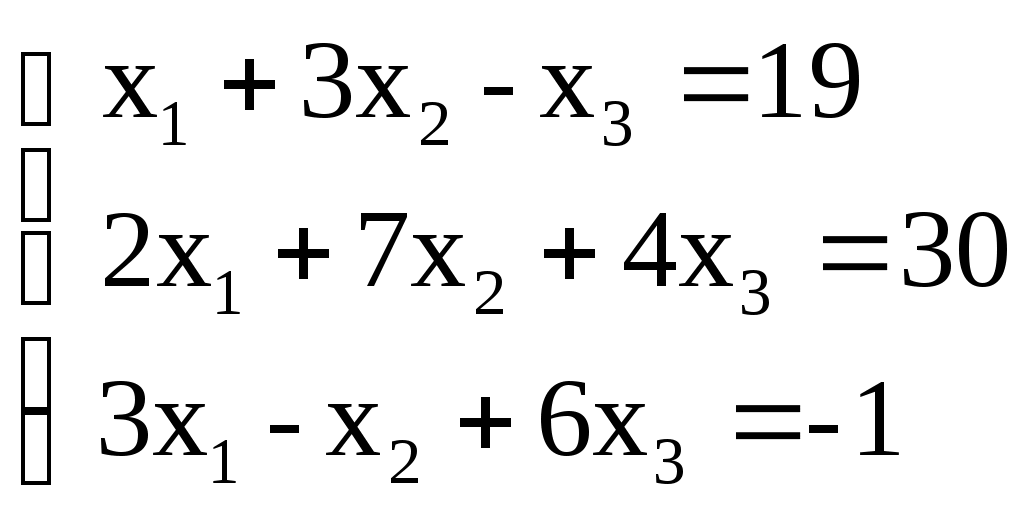
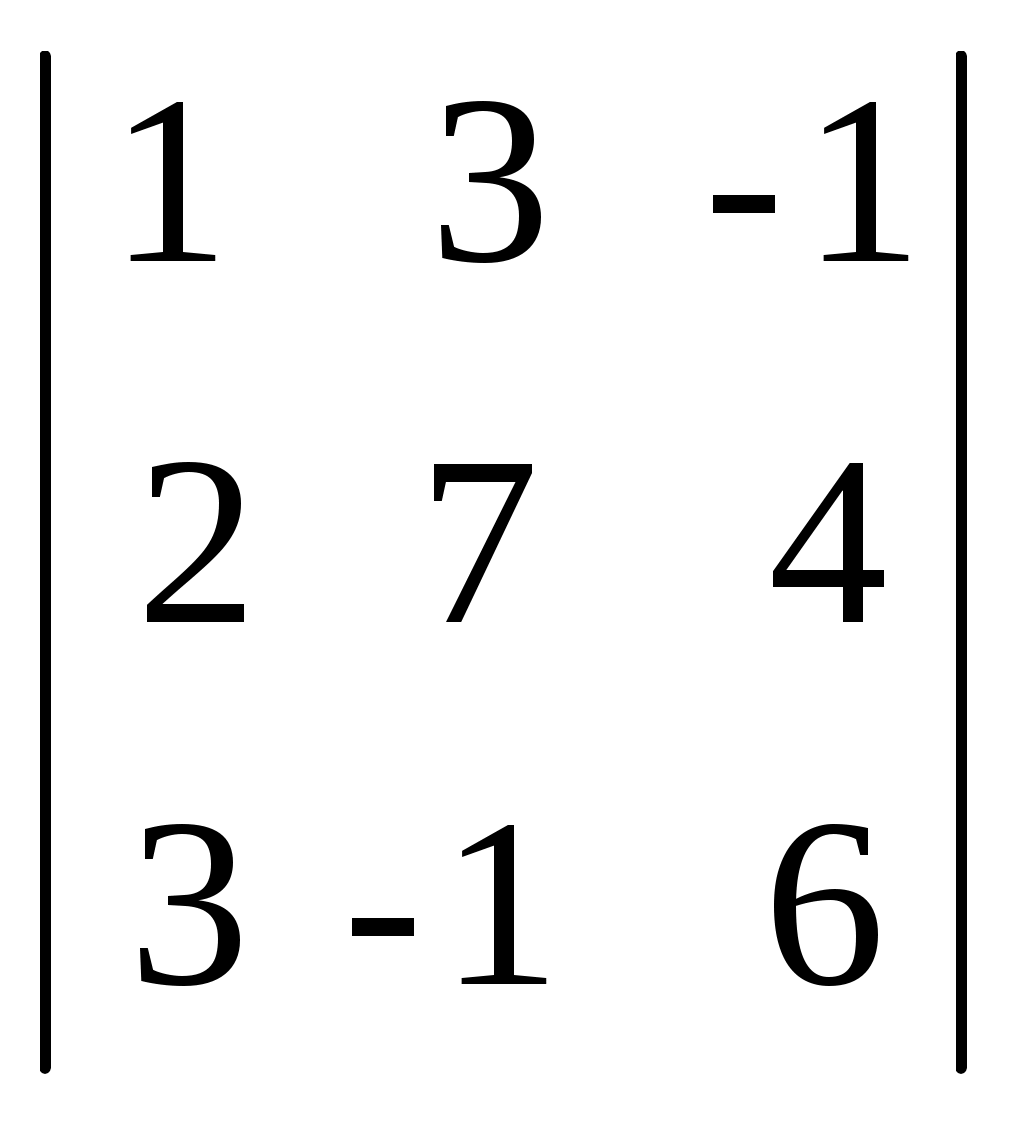 = 42+36+2-(-21+36-4) = 69 ≠ 0
= 42+36+2-(-21+36-4) = 69 ≠ 0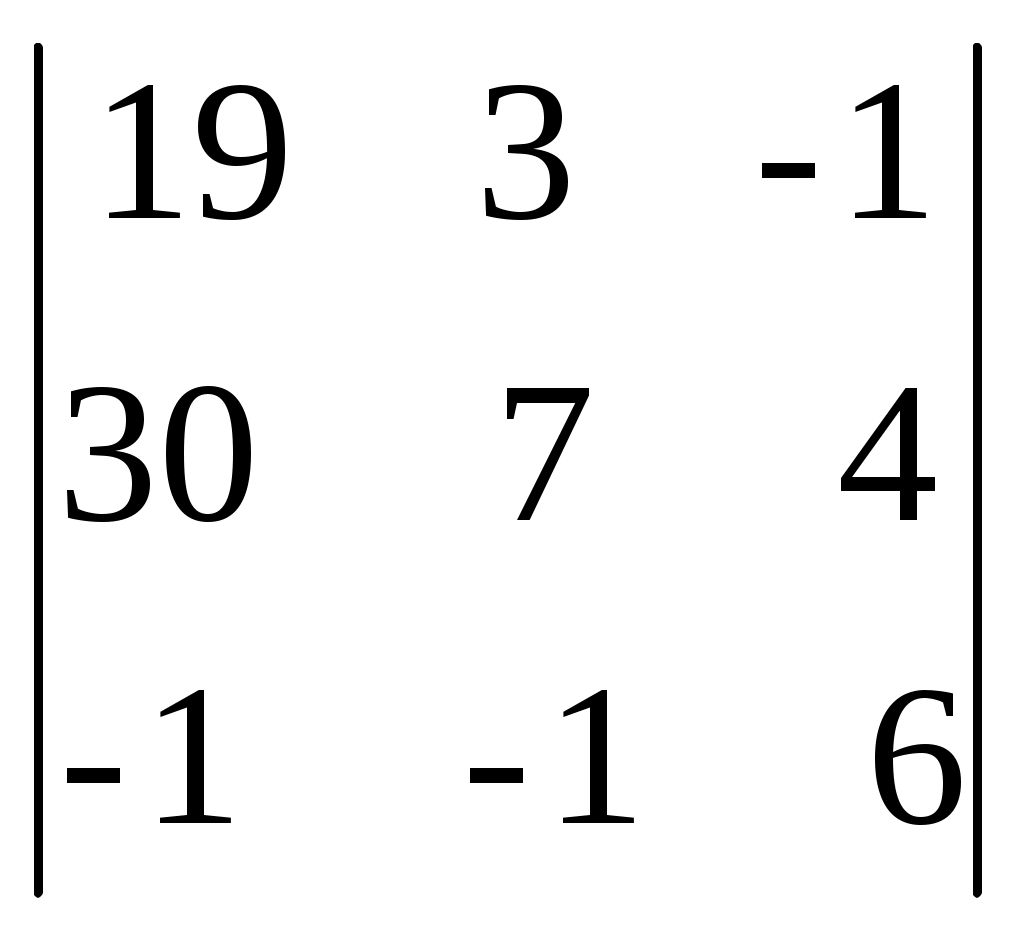 = (определитель разложим по первому столбцу) =
= (определитель разложим по первому столбцу) =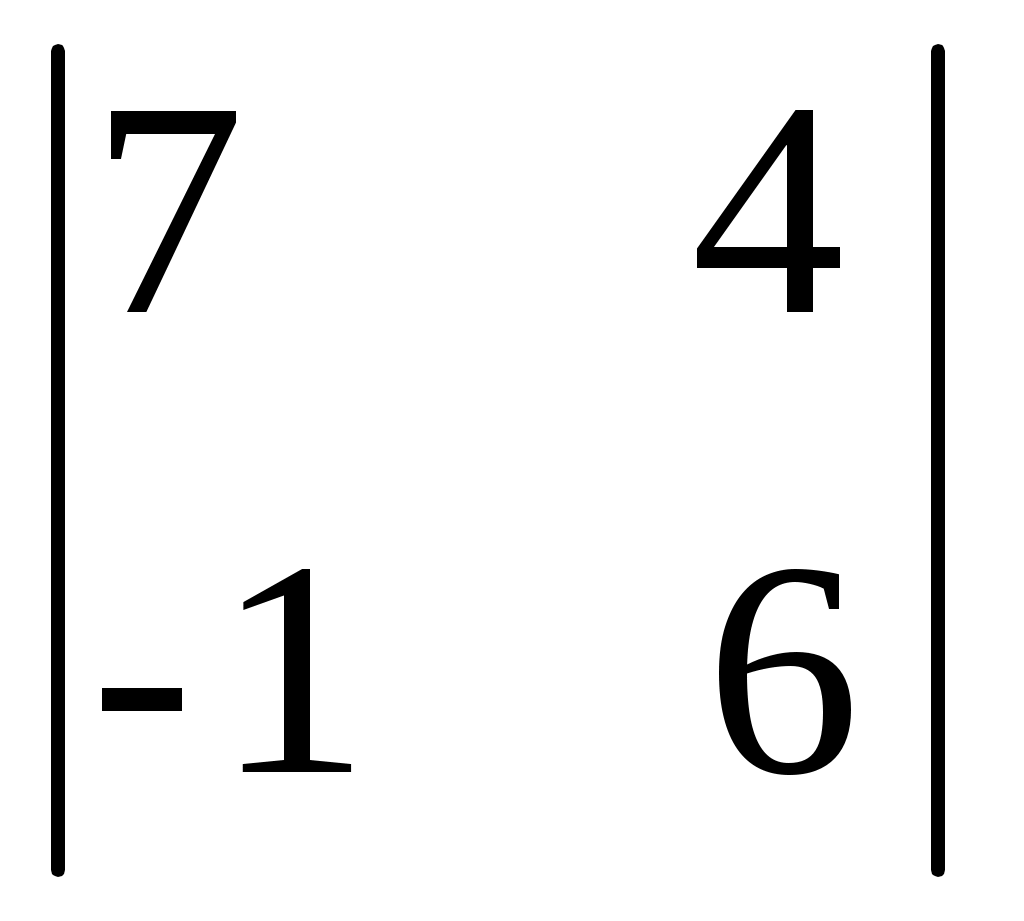 - 30 ·
- 30 · 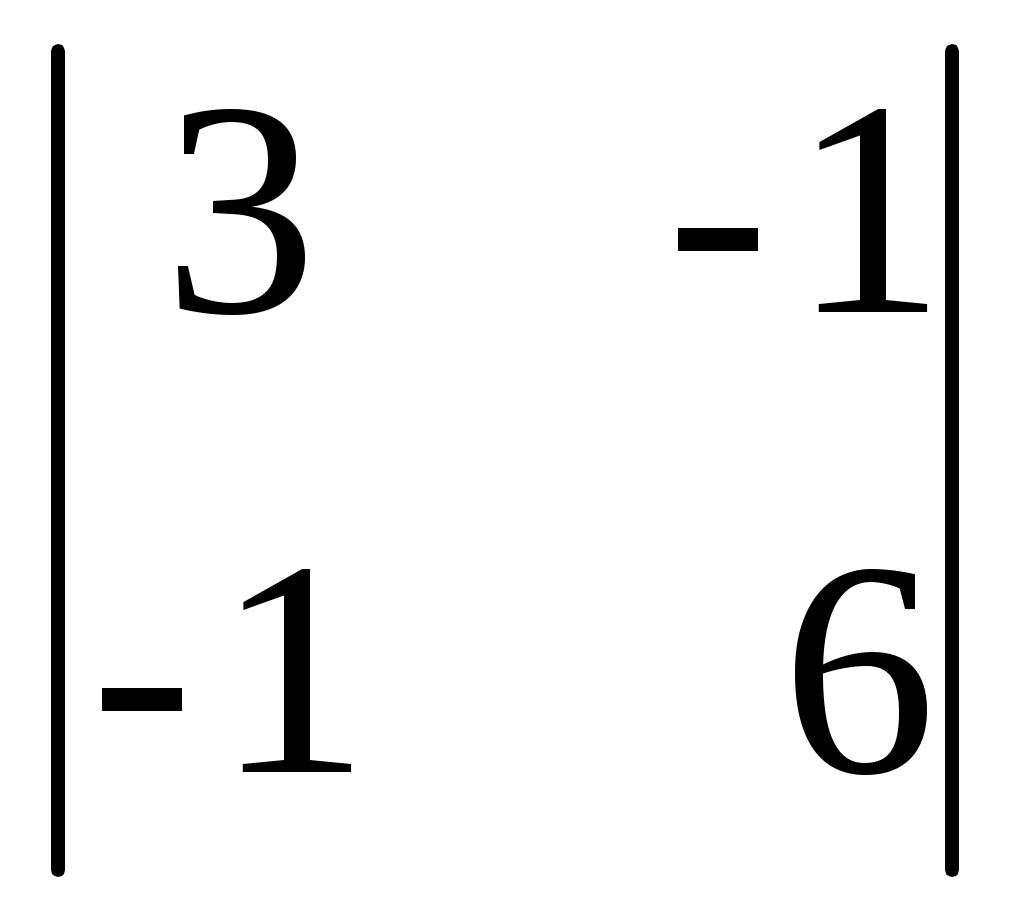 - 1 ·
- 1 · 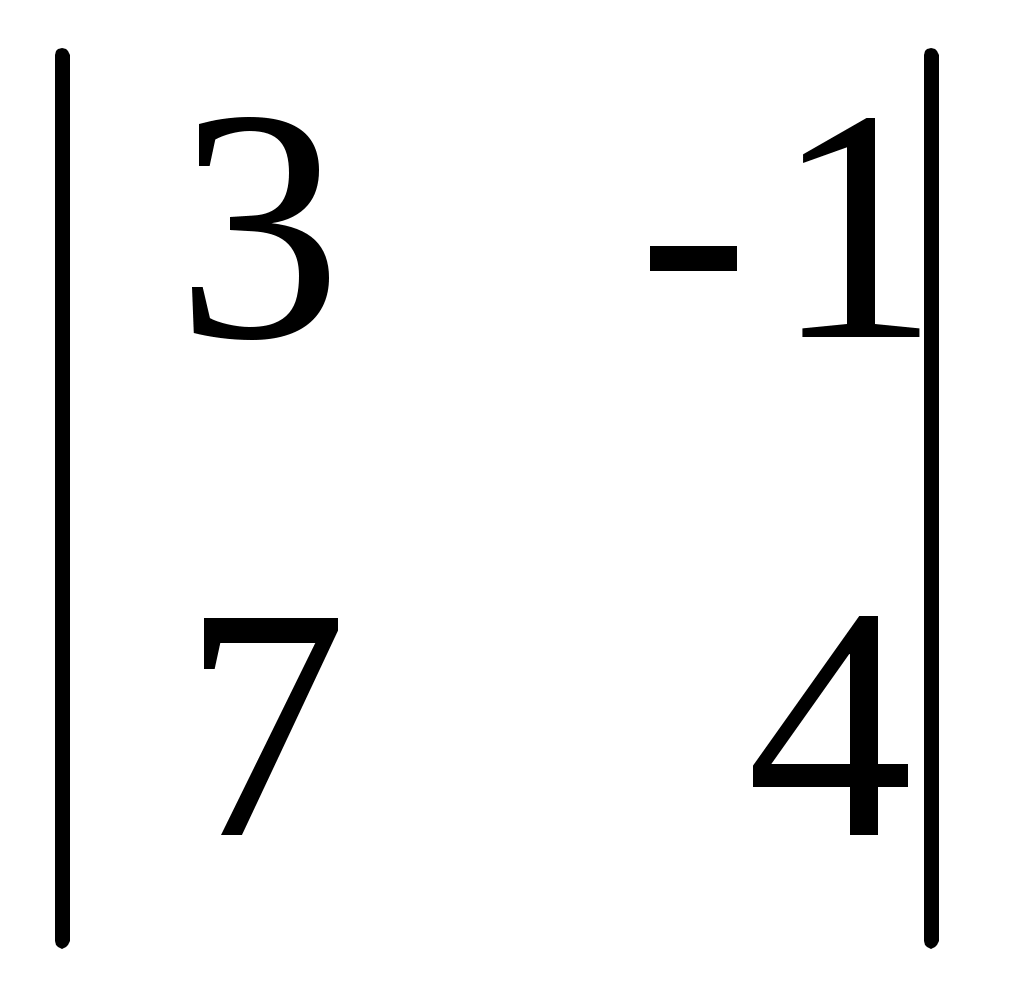 = 19·(42+4)-30·(18-1)-1·(12+7) = 19·46-
= 19·(42+4)-30·(18-1)-1·(12+7) = 19·46-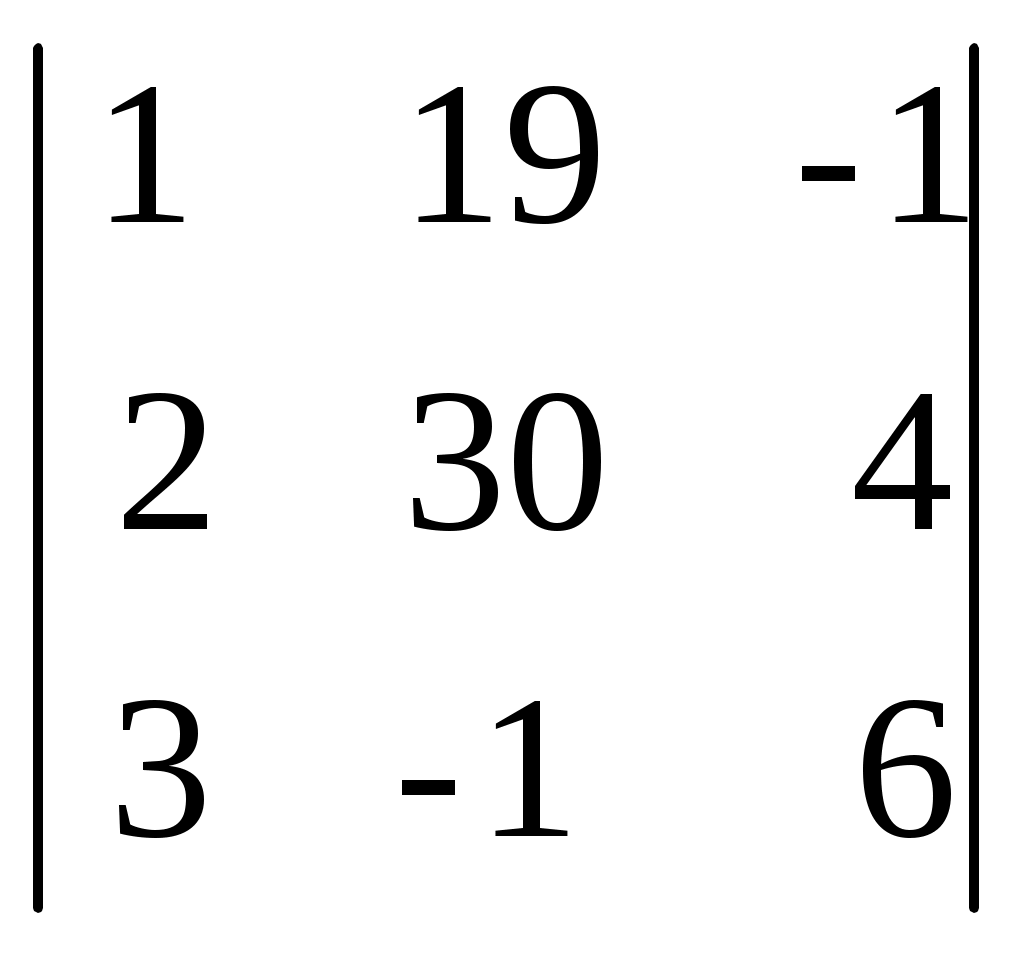 = (разложим по второму столбцу) = -19 ·
= (разложим по второму столбцу) = -19 ·  +30 ·
+30 · 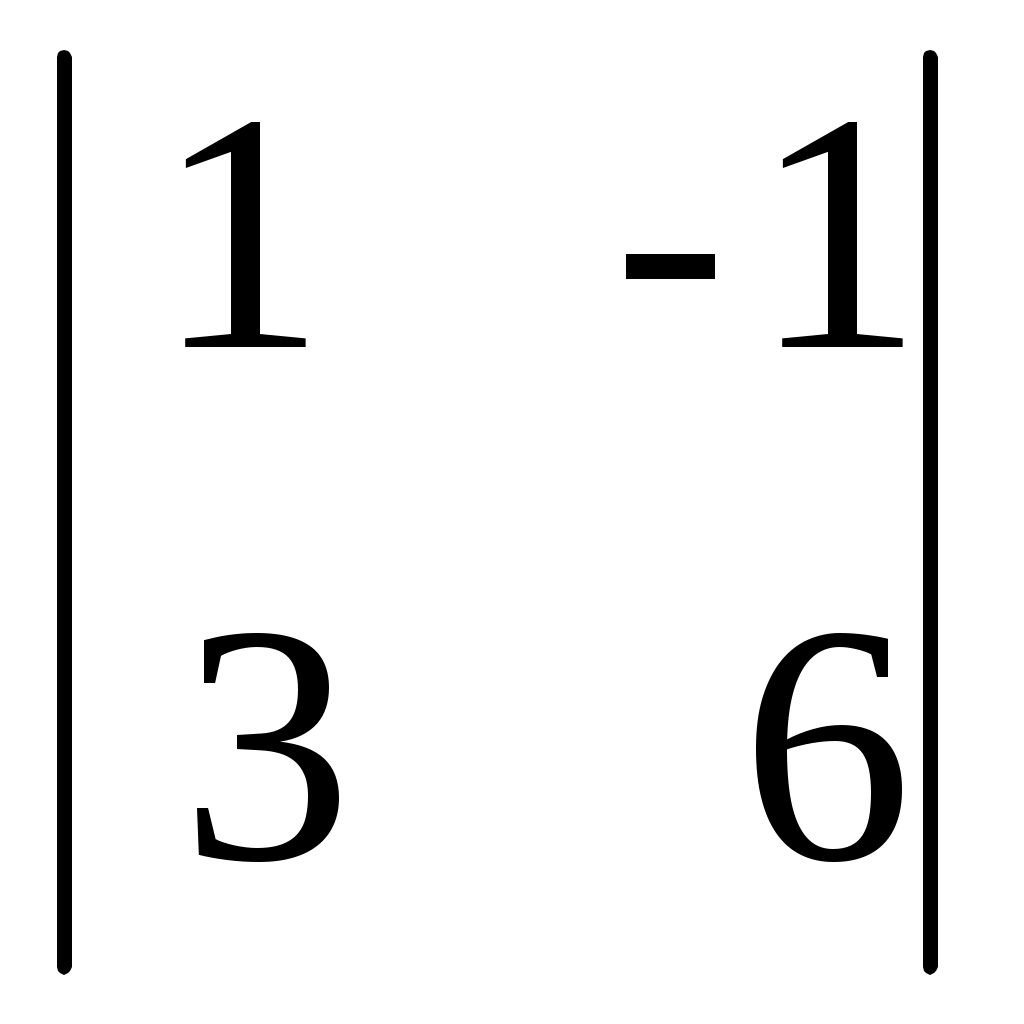
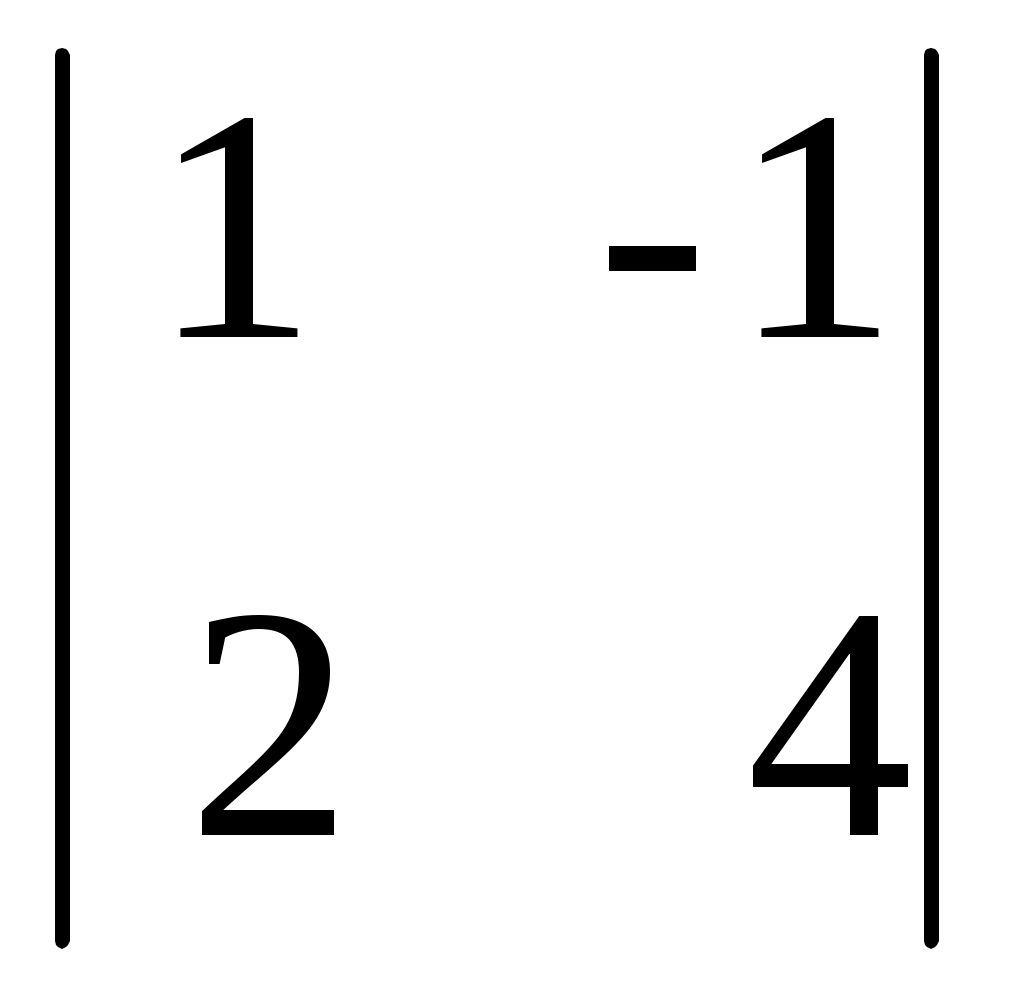 = -19·(12-12)+30·(6+3)+(4+2) = 30·9+6 = 276
= -19·(12-12)+30·(6+3)+(4+2) = 30·9+6 = 276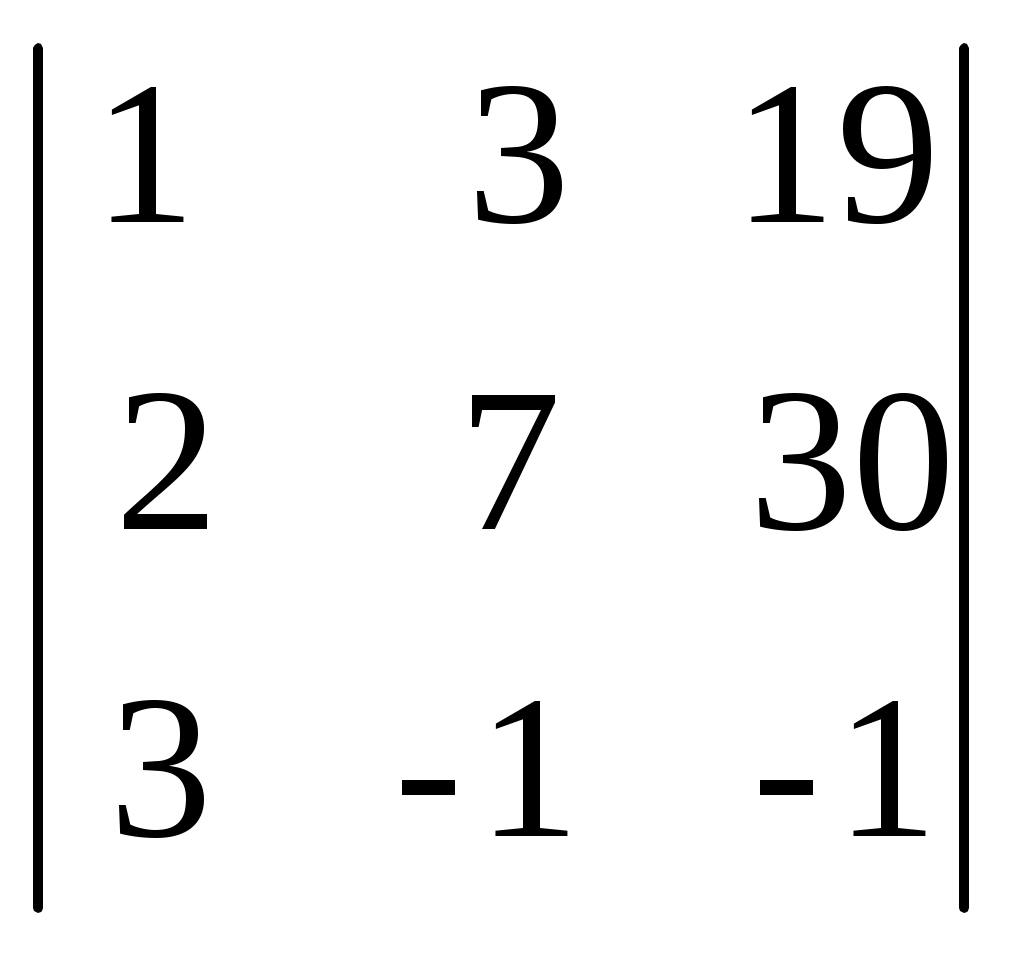 = (разложим по третьему столбцу) = 19 ·
= (разложим по третьему столбцу) = 19 · 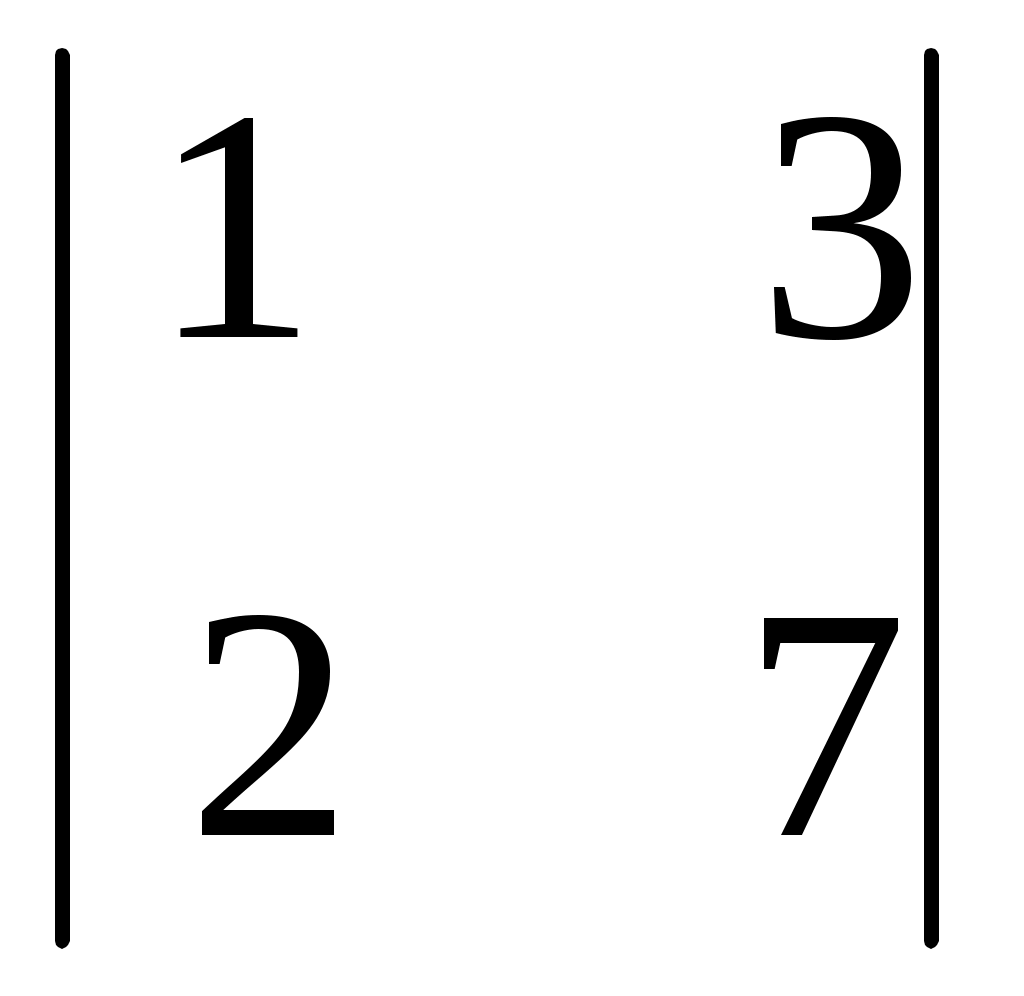 = 19·(-23)-30·(-10)-1·1 = -138
= 19·(-23)-30·(-10)-1·1 = -138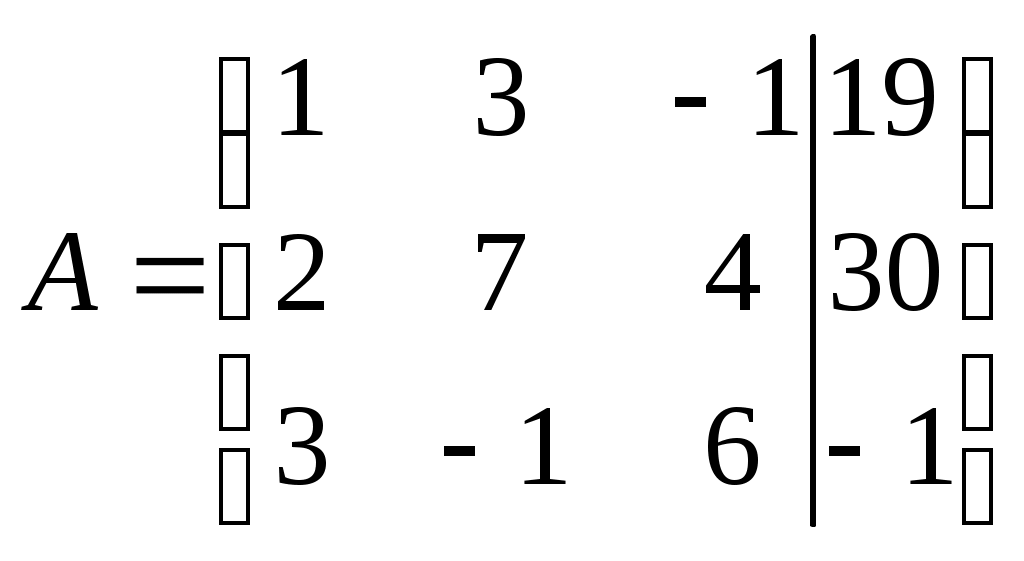
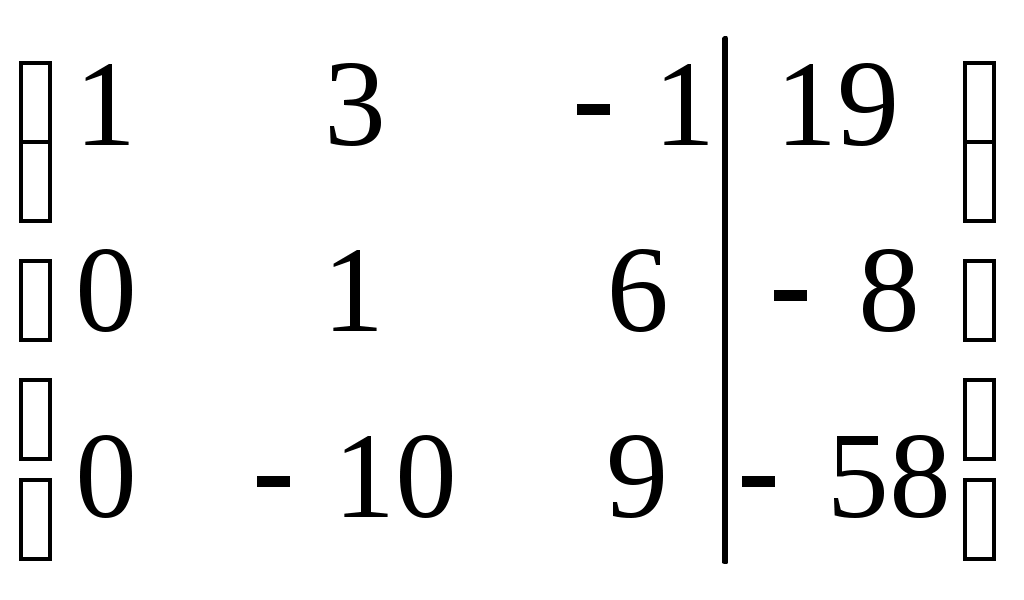
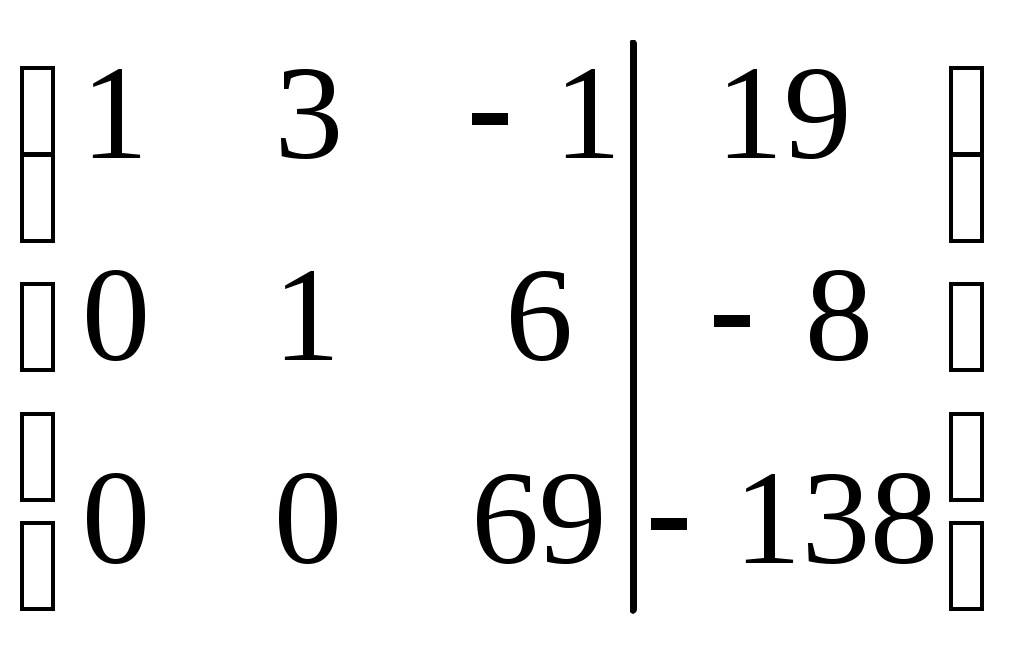
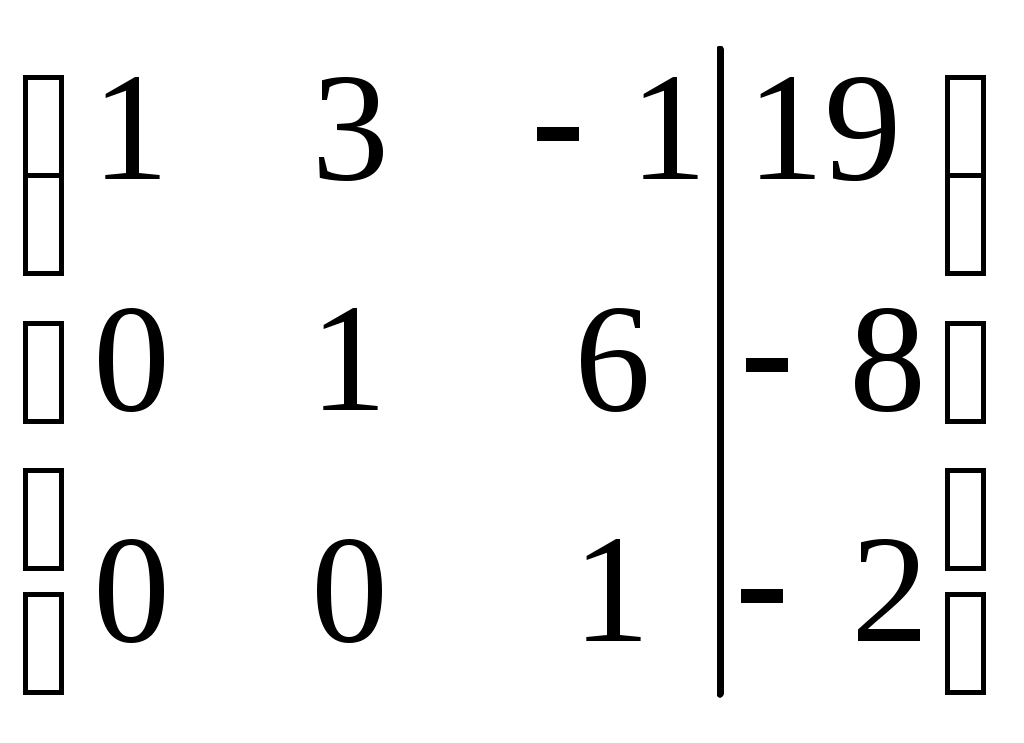
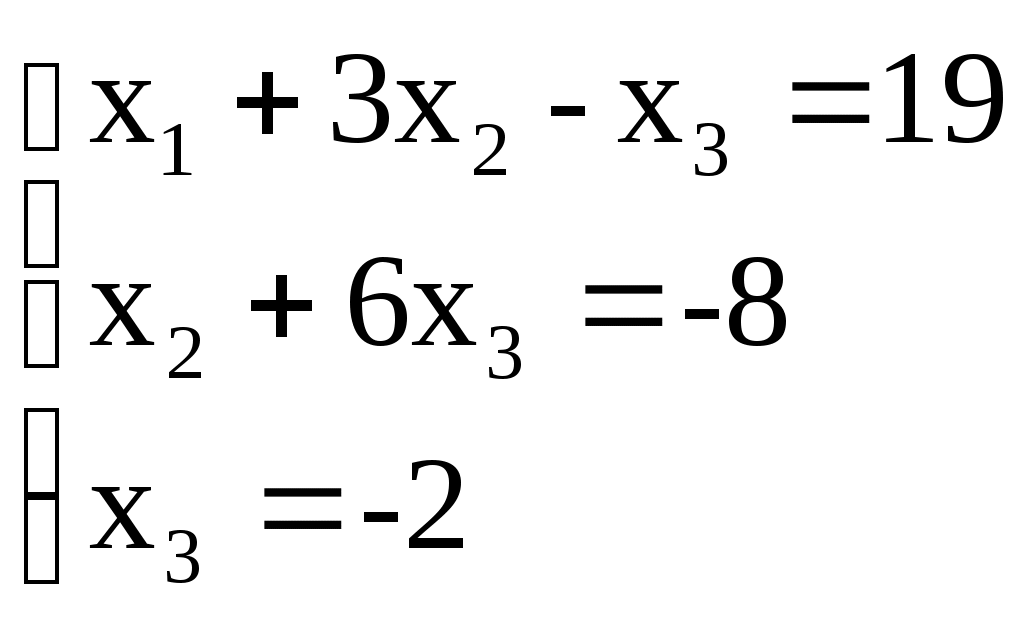 ;
; 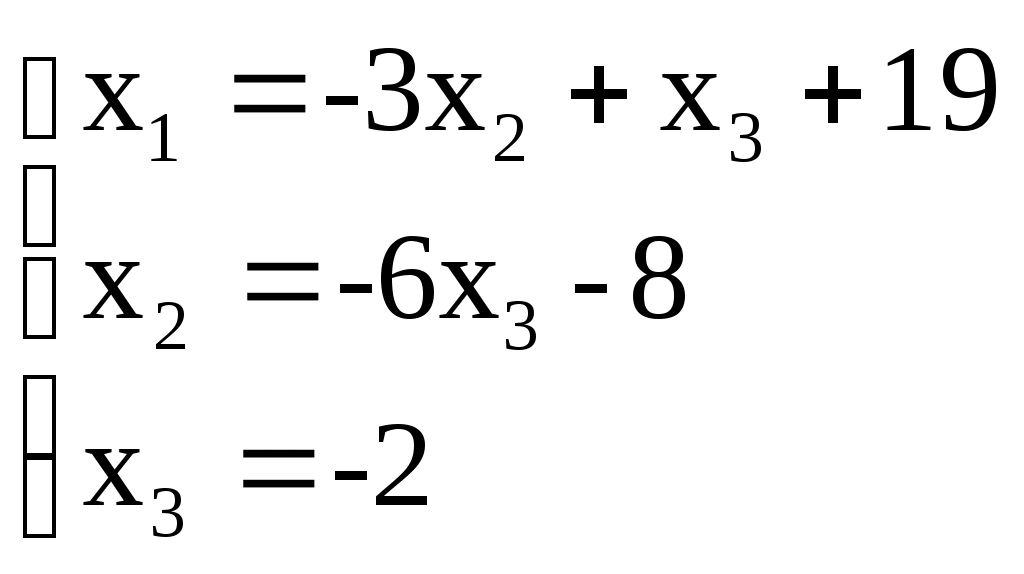 ;
;