физика. Лекция 1. Лекция 1 Механика 3 кинематика поступалтельного и вращательного движения 3
 Скачать 0.62 Mb. Скачать 0.62 Mb.
|
|
Куцов А.М. ФИЗИКА лекция 1 Механика 3 1.КИНЕМАТИКА ПОСТУПАЛТЕЛЬНОГО И ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ 3 2. ДИНАМИКА ТОЧКИ и ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА 5 3. Динамика вращательного движения твердого тела 8 4. Работа и энергия 11 5. Законы сохранения момента импульса и энергии 12 6. Элементы специальной теории относительности 13 Механика1.КИНЕМАТИКА ПОСТУПАЛТЕЛЬНОГО И ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯПоложение материальной точки в пространстве в момент времени t определяется радиус-вектором С 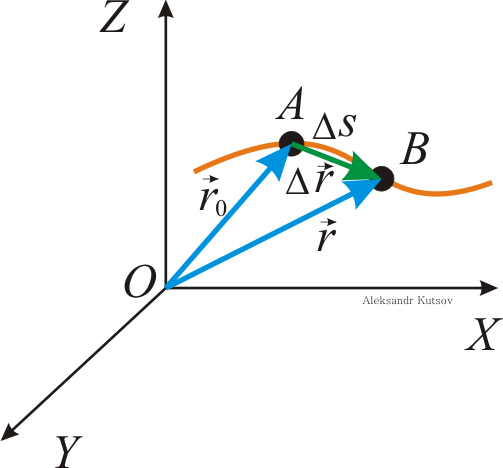 редняя скорость редняя скорость Мгновенная скорость Мгновенное ускорение Рис. 1-1. . (1.3) При криволинейном движении полное ускорение можно представить как сумму нормальной 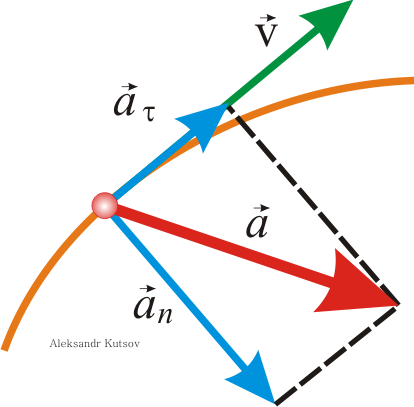 Рис 1-2. Абсолютные значения этих ускорений где R – радиус кривизны траектории. При движении с постоянным ускорением Где Скорость точки при равноускоренном движении ( Вращательное движение – это движение по круговой траектории. Это движение является частным случаем криволинейного движения, однако для его описания используются угловые характеристики: угол поворота Вектор угловой скорости направлен перпендикулярно плоскости вращения таким образом, что вращение происходит по часовой стрелке, если смотреть вдоль вектора 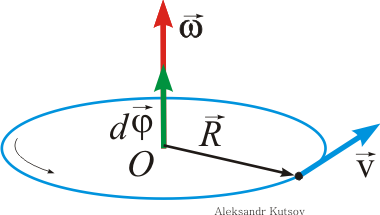 Рис. 1-3. Угловая скорость Угловое ускорение Равнопеременное вращение тела вокруг неподвижной оси Здесь знак вектора для угловой скорости и углового ускорения опущен, так как эти векторы предполагаются коллиниарными. Но следует помнить, что Связь угловых величин с линейными: путь, пройденный точкой по дуге окружности радиусом R, равен линейная скорость этой точки тангенциальное ускорение точки нормальное ускорение полное ускорение Частота вращения связанная с угловой скоростью соотношение 2. ДИНАМИКА ТОЧКИ и ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛАПервый закон Ньютона: существуют такие системы отсчета, в которых свободная материальная точка движется равномерно и прямолинейно или покоится. Эти системы отсчета называются инерциальными системами отсчета (ИСО). Второй закон Ньютона: изменение импульса материальной точки равно равнодействующей всех сил, действующих на нее Если масса постоянна, то второй закон Ньютона может быть выражен формулой Интегрируя (2.1) от 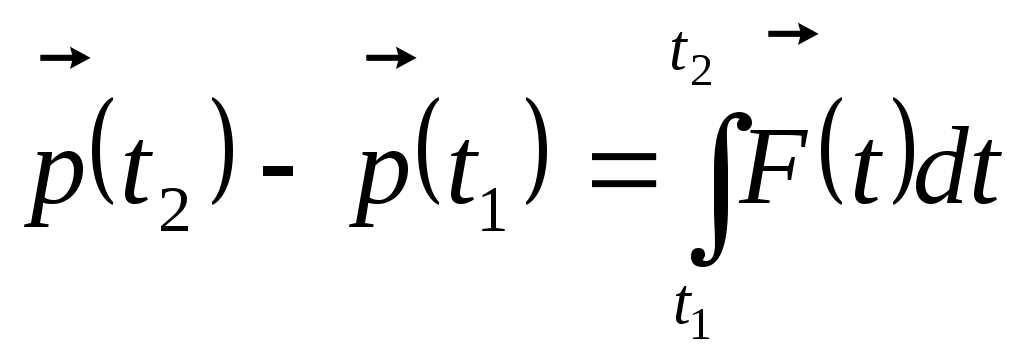 , (2.3) , (2.3)где Если, Сила, действующая на материальную точку, движущуюся по кривой, может быть разложена на две составляющие – тангенциальную и нормальную. Тангенциальная (или касательная) сила где где Сила трения скольжения где – коэффициент трения скольжения, N – абсолютная величина силы нормального давления, Сила упругости где k – коэффициент жесткости, х – координата незакрепленного конца пружины, а x0 – она же для нерастянутой пружины. Знак минус показывает, что сила направлена в обратную деформации сторону. Сила гравитационного взаимодействия где Здесь Полный импульс системы материальных точек равен сумме импульсов всех этих материальных точек Полный импульс изолированной системы материальных точек остается постоянным, как бы не двигались эти материальные точки, взаимодействуя друг с другом (закон сохранения импульса) Для двух взаимодействующих между собой материальных точек откуда следует третий закон Ньютона Применение закона сохранения импульса к соударению двух тел где При неупругом ударе, когда тела слипаются после соударения, их общая скорость Если имеется механическая система, состоящая из n материальных точек массами 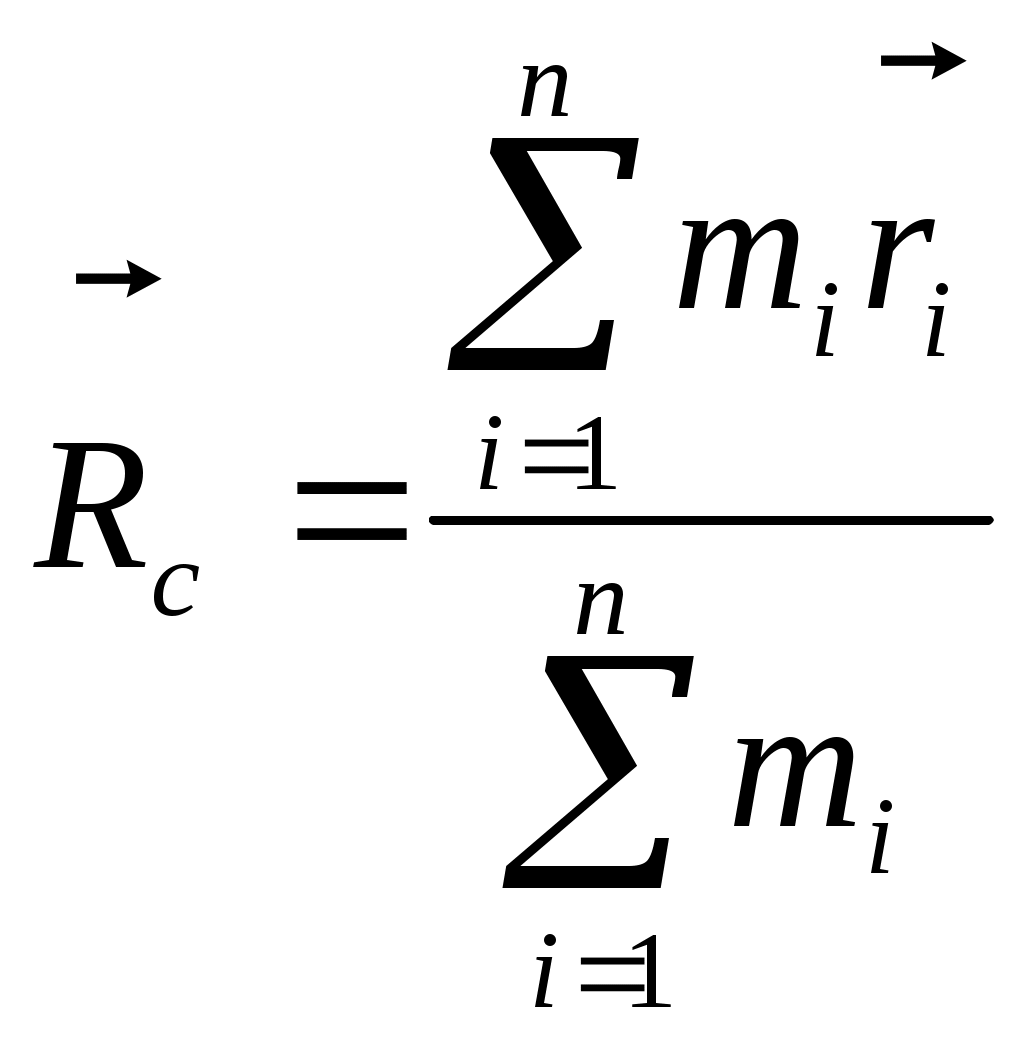 . (2.14) . (2.14)Следует понимать, что в этом месте, может не быть ни одной материальной точки, это просто удобная характеристика системы материальных точек. Центр масс 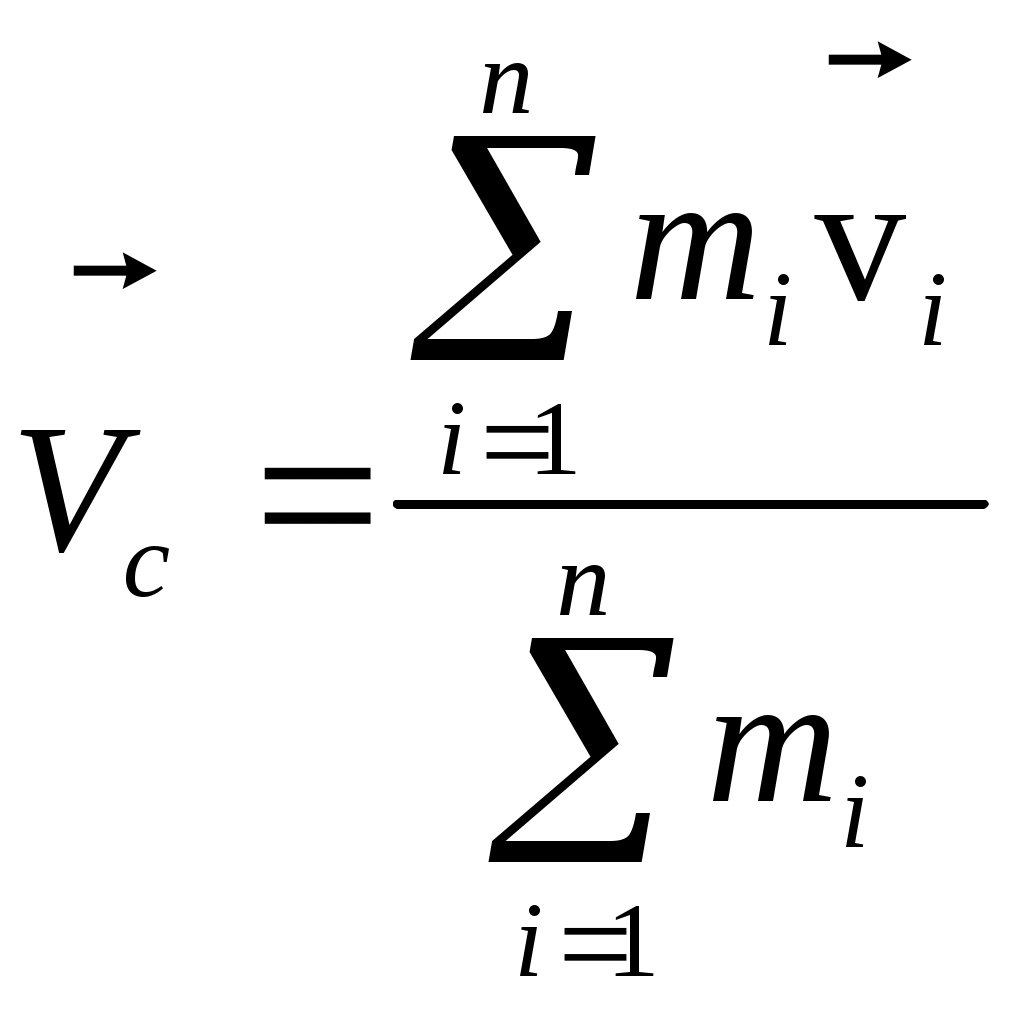 . (2.15) . (2.15)В ИСО, связанной с центром масс изолированной системы материальных точек, полный импульс равен нулю, хотя все точки находятся в движении. В этом случае говоря, что в этой ИСО материальные точки покоятся как целое. 3. Динамика вращательного движения твердого телаОсновное уравнение динамики вращательного движения твердого тела относительно неподвижной оси где Момент силы F относительно оси вращения где Момент силы относительно начала координат где 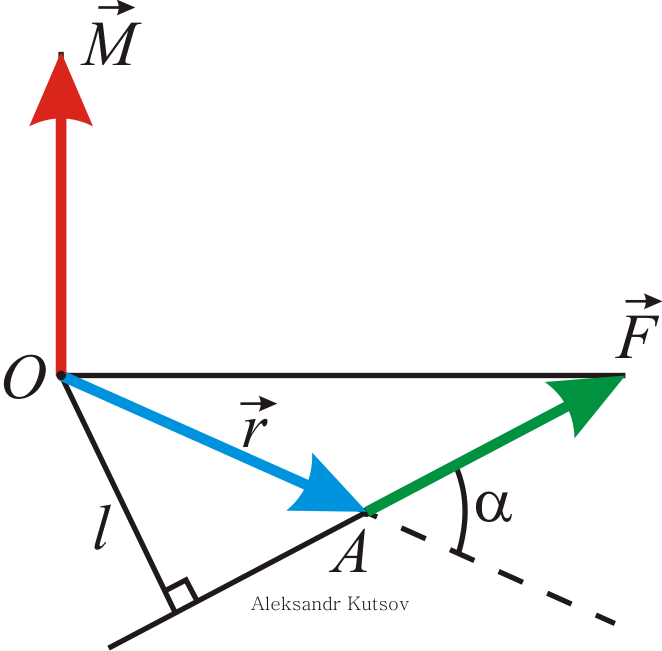 Рис. 3-1. Момент импульса тела, вращающегося относительно неподвижной оси где J – момент инерции. Момент инерции некоторых тел: а) материальной точки: где – расстояние от точки до оси вращения; б) Шара относительно оси, проходящей через его центр: где r – радиус шара; в) однородного цилиндра (диска) относительно его оси: где r – радиус основания цилиндра (диска); г) тонкого стержня относительно оси, проходящей через центр тяжести стержня и перпендикулярной ему: где l – длина стержня. Теорема Штейнера: где Момент импульса материальной точки с импульсом р относительно начала координат где 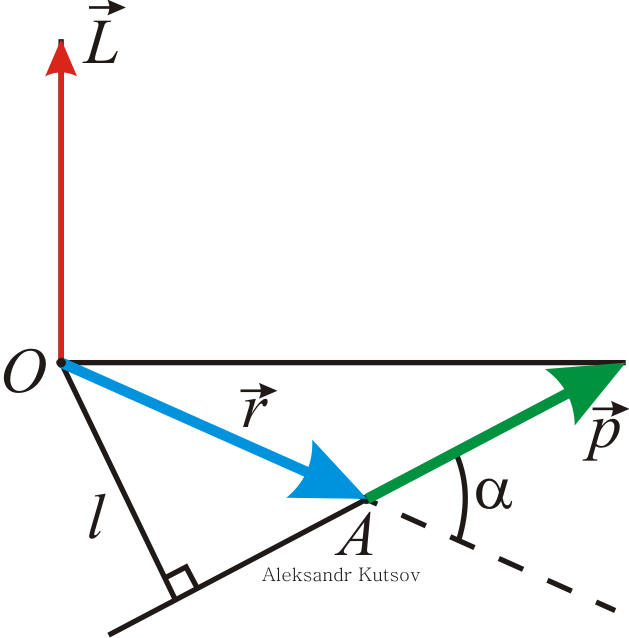 Рис. 3-2. Закон сохранения момента импульса: где Закон сохранения момента импульса для тела, вращающегося около неподвижной оси, когда момент инерции может меняться: где Элементарная работа, совершаемая силой где Кинетическая энергия: а) тела, вращающегося относительно неподвижной оси, б) тела, катящегося по плоскости 4. Работа и энергияРабота, совершаемая постоянной силой где a – угол между направлением векторов силы Работа переменной силы Мощность: а) средняя мощность за интервал времени б) мгновенная мощность Работа консервативной силы 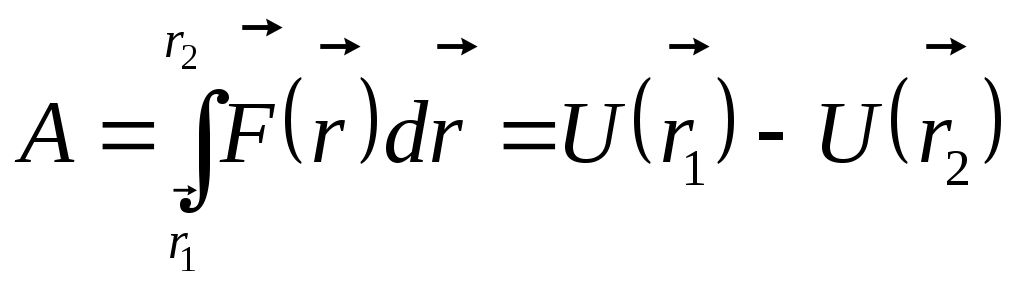 .(4.5) .(4.5)Потенциальная энергия Если потенциальная энергия где Энергия: а) кинетическая энергия тела, движущегося поступательно б) потенциальная энергия тела, поднятого на высоту h, в) потенциальная энергия упругой деформации тела где k – жесткость тела, 5. Законы сохранения момента импульса и энергииПолная механическая энергия равна сумме потенциальной U и кинетической T энергии. Закон сохранения энергии в механики: полная механическая энергия замкнутой системы, в которой действуют только консервативные силы, есть величина постоянная Закон сохранения импульса: момент импульса системы, на которую действуют внешние моменты сил, сохраняются. Особенно большое значение закон сохранения момента импульса имеет в случае движения в центральном поле сил. В этом случае момент сил равен нулю, так как 6. Элементы специальной теории относительностиВ основе специальной теории относительности (СТО), созданной А.Эйнштейном в 1905 г., лежат два постулата: Не существует абсолютно неподвижных инерциальных систем отсчета (ИСО); Скорость света c в вакууме во всех инерциальных системах отсчета одна и та же и равна 299792 м/с 3108 м/с. Непосредственным следствием второго постулата являются преобразования Лоренца, связывающие координаты и время в двух ИСО (), движущихся равномерно и прямолинейно относительно другой ( 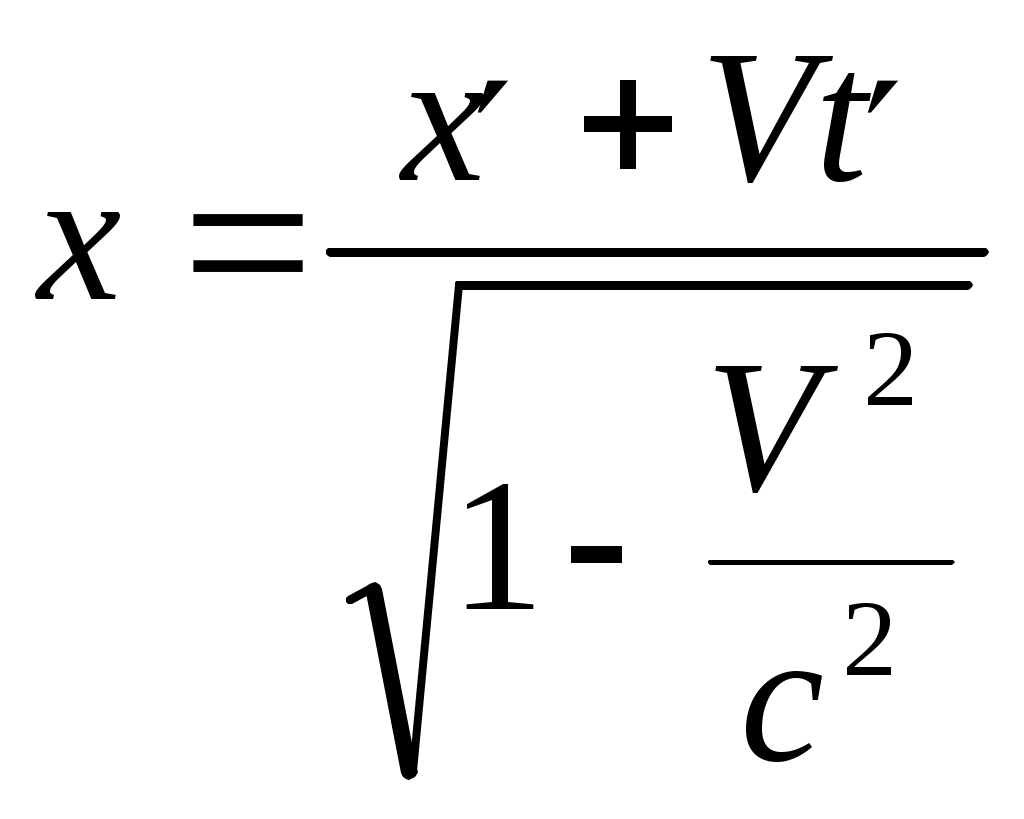 , , 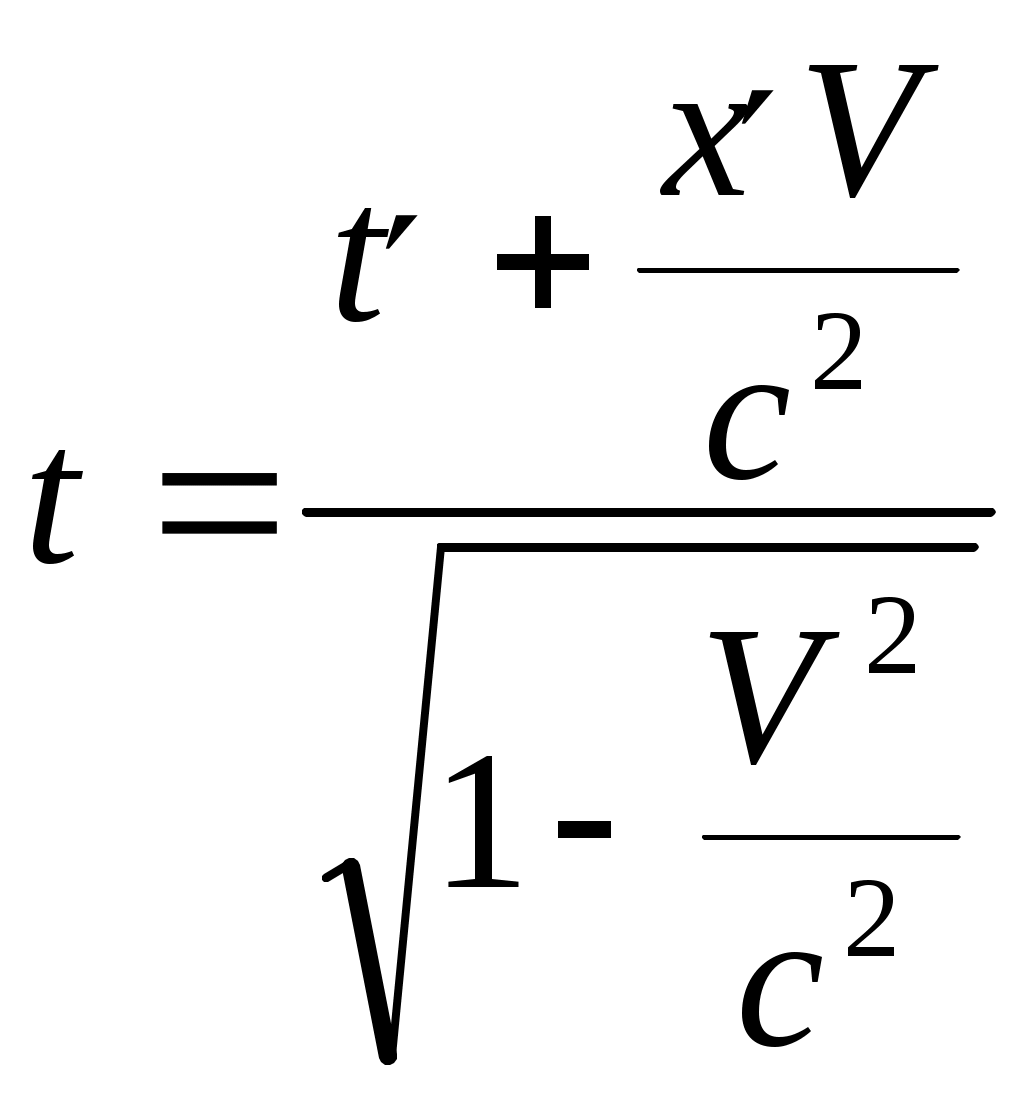 (6.1) (6.1)Это и есть преобразования Лоренца для случая, изображенного на рис. 6.1. 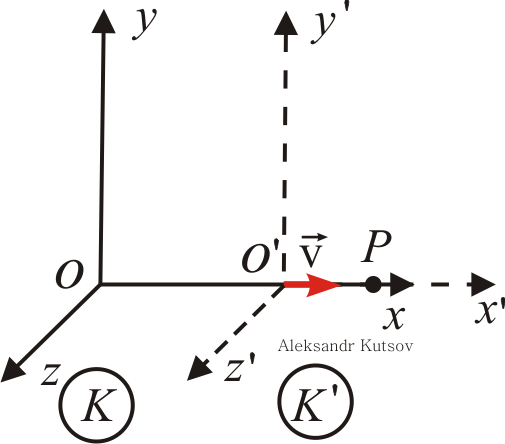 Рис. 6-1. Следствием преобразований Лоренца является релятивистское сокращение продольных размеров движущихся объектов. Если, например, неподвижный в Отметим, что поперечные размеры движущихся объектов не изменяются. Другим следствием преобразований Лоренца является замедление хода движущихся часов относительно неподвижных. В частности, если 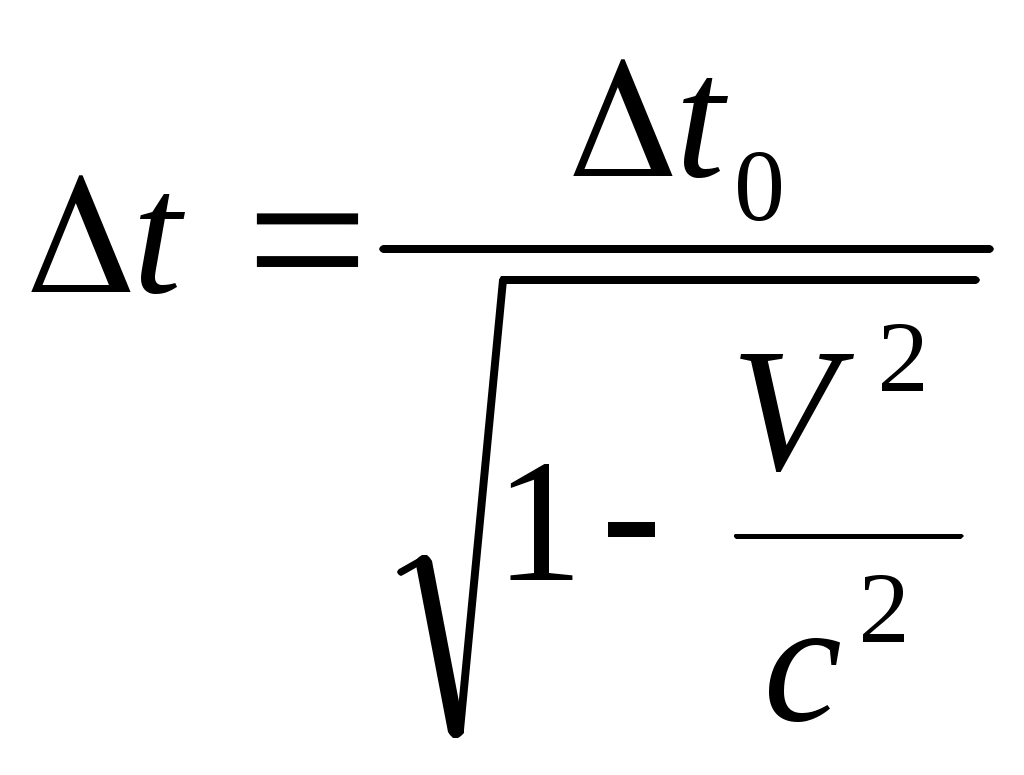 (6.3) (6.3)Тот факт, что Преобразования Лоренца приводят к иному, по сравнению с галилеевским ( 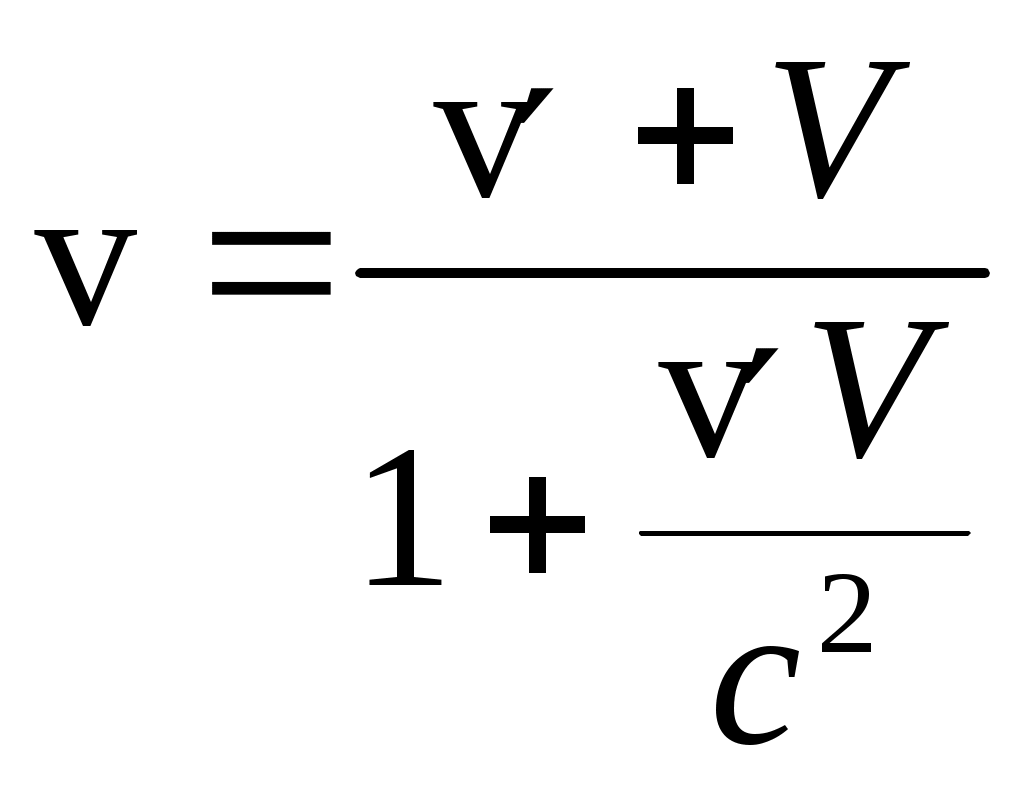 (6.4) (6.4)Из (6.4) видно, что если Релятивистский импульс частицы, движущейся со скоростью 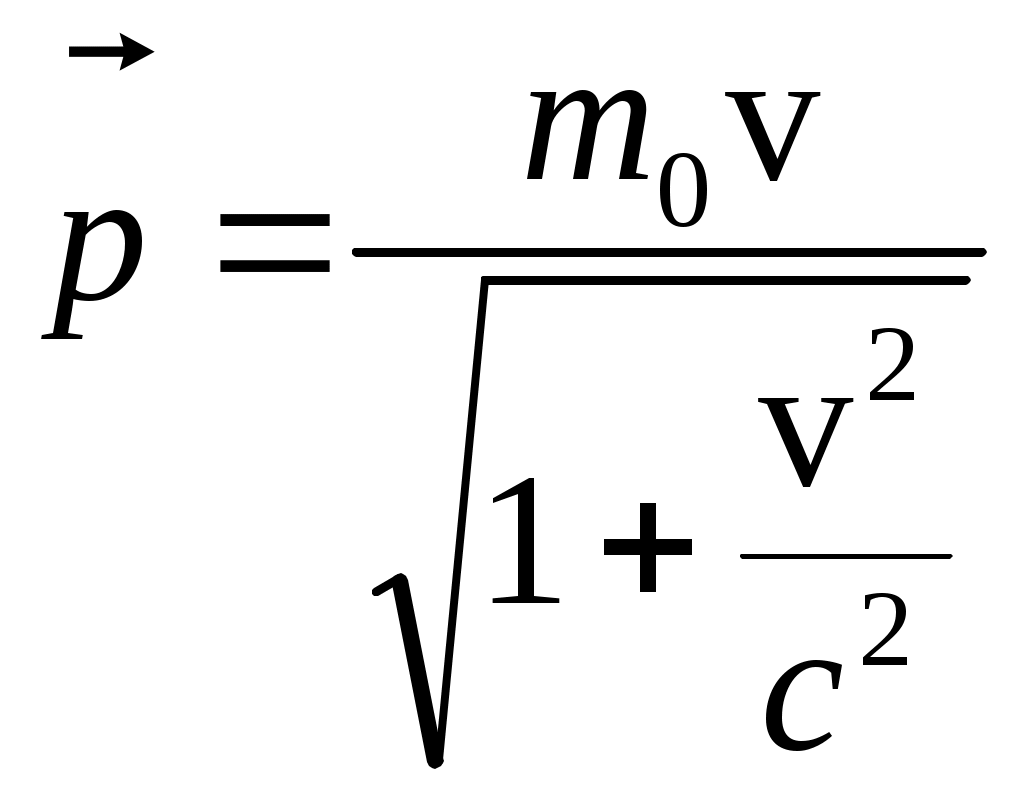 , (6.5) , (6.5)где 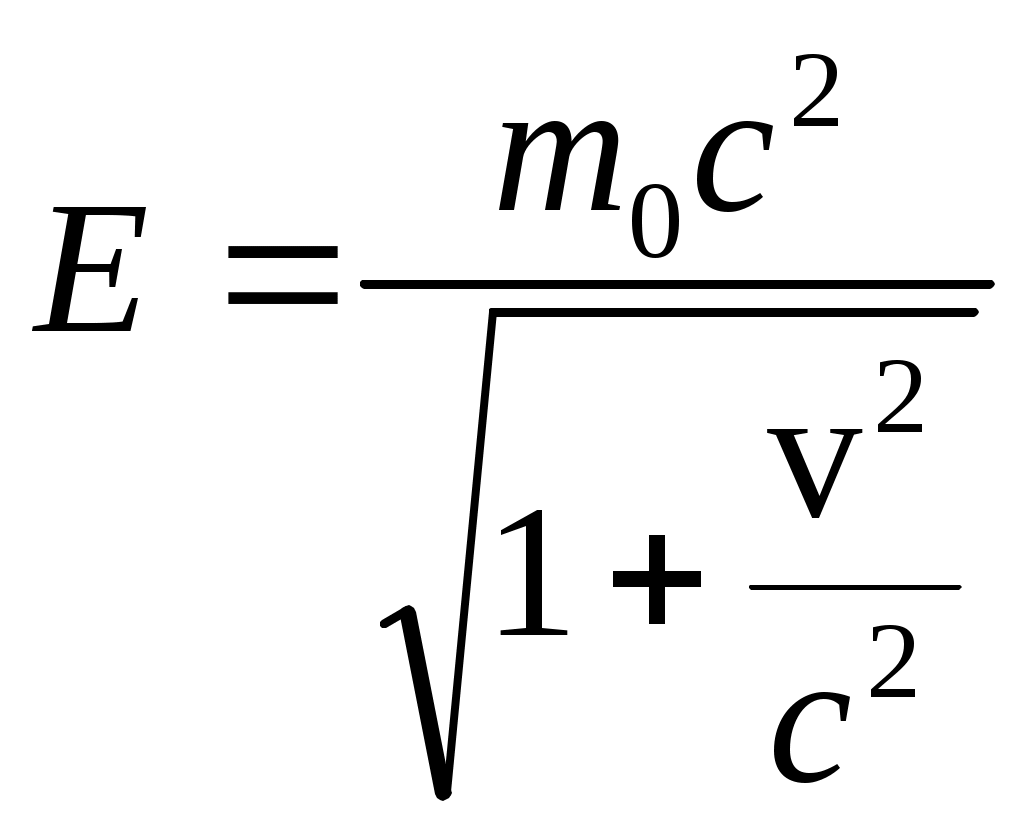 . (6.6) . (6.6)Величина называется энергией покоя. Кинетическая энергия релятивистской частицы Связь полной энергии с импульсом релятивистской частицы Для частиц с нулевой массой покоя (фотоны) |
