Інформатика_Лекції_2010. Лекція 1. Предмет та основні поняття інформатики
 Скачать 187.89 Kb. Скачать 187.89 Kb.
|
Позиційні системи численняЗагальноприйнятою в сучасному світі є десяткова позиційна система числення, яка з Індії через арабські країни прийшла в Європу. Основою цієї системи є число десять. Основою системи числення називається число, яке означає, у скільки разів одиниця наступного розрядку більше за одиницю попереднього. Загальновживана форма запису числа є насправді не що інше, як скорочена форма запису розкладу за степенями основи системи числення, наприклад 130678=1*105+3*104+0*103+6*102+7*101+8 Тут 10 є основою системи числення, а показник степеня - це номер позиції цифри в записі числа (нумерація ведеться зліва на право, починаючи з нуля). Арифметичні операції у цій системі виконують за правилами, запропонованими ще в середньовіччі. Наприклад, додаючи два багатозначних числа, застосовуємо правило додавання стовпчиком. При цьому все зводиться до додавання однозначних чисел, для яких необхідним є знання таблиці додавання. Проблема вибору системи числення для подання чисел у пам'яті комп'ютера має велике практичне значення. В разі її вибору звичайно враховуються такі вимоги, як надійність подання чисел при використанні фізичних елементів, економічність (використання таких систем числення, в яких кількість елементів для подання чисел із деякого діапазону була б мінімальною). Для зображення цілих чисел від 1 до 999 у десятковій системі достатньо трьох розрядів, тобто трьох елементів. Оскільки кожен елемент може перебувати в десятьох станах, то загальна кількість станів - 30, у двійковій системі числення 99910=1111100, необхідна кількість станів - 20 (індекс знизу зображення числа - основа системи числення). У такому розумінні є ще більш економічна позиційна система числення - трійкова. Так, для запису цілих чисел від 1 до у десятковій системі числення потрібно 90 станів, у двійковій - 60, у трійковій - 57. Але трійкова система числення не дістала поширення внаслідок труднощів фізичної реалізації. Тому найпоширенішою для подання чисел у пам'яті комп'ютера є двійкова система числення. Для зображення чисел у цій системі необхідно дві цифри: 0 і 1, тобто достатньо двох стійких станів фізичних елементів. Ця система є близькою до оптимальної за економічністю, і крім того, таблички додавання й множення в цій системі елементарні:
Оскільки 23=8, а 24=16 , то кожних три двійкових розряди зображення числа утворюють один вісімковий, а кожних чотири двійкових розряди - один шістнадцятковий. Тому для скорочення запису адрес та вмісту оперативної пам'яті комп'ютера використовують шістнадцяткову й вісімкову системи числення. Нижче в таблиці 1 наведені перших 16 натуральних чисел записаних в десятковій, двійковій, вісімковій та шістнадцятковій системах числення. Таблиця 1
В процесі налагодження програм та в деяких інших ситуаціях у програмуванні актуальною є проблема переведення чисел з однієї позиційної системи числення в іншу. Якщо основа нової системи числення дорівнює деякому степеню старої системи числення, то алгоритм переводу дуже простий: потрібно згрупувати справа наліво розряди в кількості, що дорівнює показнику степеня і замінити цю групу розрядів відповідним символом нової системи числення. Цим алгоритмом зручно користуватися коли потрібно перевести число з двійкової системи числення у вісімкову або шістнадцяткову. Наприклад, 101102=10110=268, 10111002=101 1100=5C8 у двійковому відбувається за зворотнім правилом: один символ старої системи числення заміняється групою розрядів нової системи числення, в кількості рівній показнику степеня нової системи числення. Наприклад, 4728=100 111 010=1001110102, B516=10110101=101101012 Як бачимо, якщо основа однієї системи числення дорівнює деякому степеню іншої, то перевід тривіальний. У протилежному випадкові користуються правилами переведення числа з однієї позиційної системи числення в іншу (найчастіше для переведення із двійкової, вісімкової та шістнадцяткової систем числення у десяткову, і навпаки). Алгоритми переведення чисел з однієї позиційної системи числення в іншу1. Для переведення чисел із системи числення з основою p в систему числення з основою q, використовуючи арифметику нової системи числення з основою q, потрібно записати коефіцієнти розкладу, основи степенів і показники степенів у системі з основою q і виконати всі дії в цій самій системі. Очевидно, що це правило зручне при переведенні до десяткової системи числення. Наприклад: з шістнадцяткової в десяткову: 92C816=9*10163+2*10162+C*10161+8*10160= 9*16103+2*16102+12*16101+8*16100=37576 з вісімкової в десяткову: 7358=7*1082+3*1081+5*1080= 7*8102+3*8101+5*8100=47710 з двійкової в десяткову: 1101001012=1*1028+1*1027+ 0*1026+1*1025+0*1024+0*1023+ 1*1022+0*1021+1*1020= 1*2108+1*2107+0*2106+1*2105+ 0*2104+0*2103+1*2102+0*2101+ 1*2100=42110 2. Для переведення чисел із системи числення з основою p в систему числення з основою q з використанням арифметики старої системи числення з основою p потрібно:
Цим самим правилом зручно користуватися в разі переведення з десяткової системи числення, тому що її арифметика для нас звичніша. Приклади: 999,3510=1111100111,010112 для цілої частини: 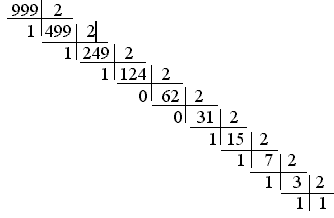 для дробової частини: 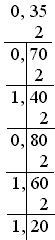 Контрольні запитання
Лекція №3. Архітектура обчислювальних систем. Сукупність пристроїв, призначених для автоматичної або автоматизованої обробки інформації називають обчислювальною технікою. Конкретний набір, пов'язаних між собою пристроїв, називають обчислювальною системою. Центральним пристроєм більшості обчислювальних систем є електронна обчислювальна машина (ЕОМ) або комп'ютер. |
