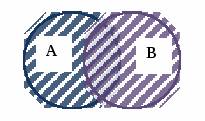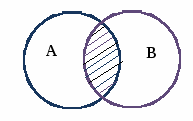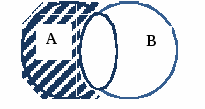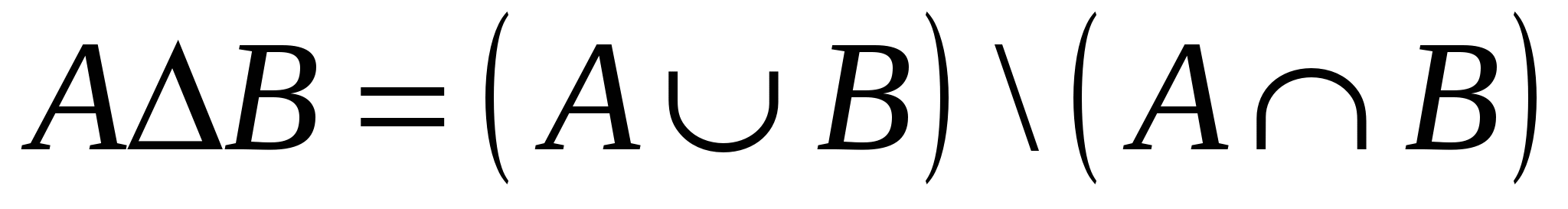Лекція № 1 Основні поняття теорії множин. Лекція 1 з навчальної дисципліни Дискретна математика Тема Основні поняття теорії множин. Заняття Основні поняття теорії множин
 Скачать 431 Kb.
|
|
Державний університет телекомунікацій Навчально-науковий інститут Захисту інформації Кафедра вищої математики
ЛЕКЦІЯ № 1 з навчальної дисципліни Дискретна математика Тема № 1. Основні поняття теорії множин. Заняття № 1. Основні поняття теорії множин Навчальний час – 2 години Для студентів денної форми навчання освітньо-кваліфікаційного рівня бакалавр напряму підготовки 6.050102 – Комп’ютерна інженерія Навчальна та виховна мета: 1. Сформувати базові знання з основ теорії множин; 2. Формувати здатність учитися, здатність до системного мислення. Лекція розроблена доцентом кафедри ВМ, к.т.н. Скубаком О.М.
Київ – 2014 Зміст Вступ. Зміст та задачі дискретної математики. 1. Поняття множини. 2. Способи задання множини. 3. Відношення між множинами. Геометричне зображення множин. 4. Основні операції над множинами. 5. Властивості операцій над множинами. 6. Декартовий добуток множин. Заключна частина. ЛIТЕРАТУРА 1. Бардачов Ю.М. та ін. Дискретна математика. – К.: Вища школа, 2002. – 287с. – с. 14-21. Завдання на самостійну роботу 1. Опрацювати лекційний матеріал. 2. Опрацювати матеріал за підручником 3. Підготовитися до практичного заняття 1. Конспект лекції Вступ. Зміст та задачі дискретної математики Дискретна математика (скінчена математика) – розділ математики, що вивчає властивості об’єктів дискретного характеру. Під дискретними об’єктами в математиці розуміють ті, які в сукупності утворюють скінченну або зчисленну множину. Дискретні об’єкти принципово відрізняються від неперервних (таких, наприклад, як всі дійсні числа з відрізку  ).Основними задачами дискретної математики є:
1. Поняття множини. Способи задання множини Поняття множини і її елемента відносять до основних, первинних понять математики. Вважають, що ці поняття не визначаються. Під множиною розуміють сукупність певних об’єктів, які об’єднані спільними властивостями. При цьому природа самих об'єктів, що становлять ту або іншу множину нас не буде цікавити. Об’єкти будь-якої природи, що утворюють множину, називаються її елементами. Для позначення конкретних множин використовують великі букви латинського алфавіту:  або великі букви з індексами  .Для позначення елементів множин використовують малі букви латинського алфавіту:  або малі букви з індексами  . Належність елемента множині позначається символом  :  – елемент  належить множині  , неналежність елемента множині позначається символом  :  .Означення. Множина називається скінченною, якщо вона складається із скінченного числа елементів. Кількість елементів у скінченній множині називається потужністю множини и позначається  . Множину потужності  ( ), тобто таку, яка складається з елементів, часто називають ще -множиною. Множина, що не містить жодного елемента, називається порожньою і позначається символом  . Множина, що містить всі елементи, що знаходяться в розгляді, називається універсальною або універсумом і позначається  .Множина вважається заданою, якщо про будь-який її елемент можна сказати, належить він цій множині чи не належить. 2. Способи задання множин 1. Перелік елементів – найбільш природний спосіб задання множини, коли множина , яка складається з елементів  , задається списком своїх елементів:  , де порядок слідування елементів значення не має. Наприклад:   .Вважається, що всі елементи множини різні. 2. За допомогою характеристичної властивості елементів – універсальний спосіб задання множини, коли властивості її елементів можуть бути описані виразом  (елементи  даної множини і тільки вони мають властивість  ). Записують  . Наприклад:  3. Аналітичний, за допомогою символів операцій над множинами та дужок (буде розглянуто нижче). 3. Відношення між множинами. Геометричне зображення множин Означення. Множина  називається підмножиною множини , якщо кожен елемент множини належить множині . Позначення:  ( ) – « включається в » ( включає ), де  – знак нестрогого включення.  .Наприклад:  ,  , – – підмножина .Означення. Множини і називаються рівними, якщо вони складаються з одних і тих самих елементів, тобто  і . і .Якщо и  , то називається власною, строгою чи істинною підмножиною . Позначення:  , де  – знак строгого включення.Очевидно, що для будь-якої множини  і  . і називаються невласними підмножинами множини .Для кожної множини існує множина, елементами якої є всі її підмножини.Означення. Множина, елементами якої є всі підмножини множини і тільки вони, називається булеаном (або множиною підмножин) множини і позначається  . Відносно елементів булеана множина є універсумом. (Тобто, універсальна множина – це множина, підмножинами якої є всі множини, що розглядаються,)У разі скінченної підмножини , що складається з  елементів, булеан містить  елементів: .Приклад.Якщо  , то  . Перша й остання підмножини невласні, інші – власні.Порожня множина має властивість:  при будь-якому  . Універсальна множина  має властивість:  при будь-якому .Множини і відношення між ними зручно задавати графічно за допомогою так званих діаграм Ейлера-Венна. Діаграми Ейлера-Венна є геометричним зображенням множин. Множина зображується замкненою кривою довільної форми (найчастіше – кругом). Точки, які лежать всередині замкненої кривої, можна розглядати як елементи відповідної множини. Наприклад: 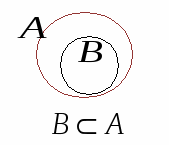 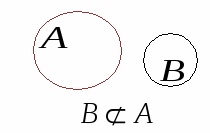 Універсум 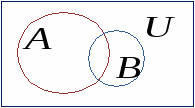на діаграмах Ейлера-Венна зображується у вигляді прямокутника. 3. Основні операції над множинами Існує ще один спосіб задання множин – за допомогою операцій над іншими множинами. На булеані  визначаються наступні операції над множинами  і  .
Використовуючи операції ∩¸  ¸ \¸  можна виражати одні множини через інші. За умовчанням приймається пріоритет операцій:  . Для зміни цього порядку у виразі використовують дужки.Таким чином, множину можна задати виразом, в який входять множини, операції і, може бути, дужки. Такий спосіб завдання множини називається аналітичним. 4. Властивості операцій над множинами Операції над множинами, як і операції над числами, мають певні властивості. Ці властивості виражаються сукупністю тотожностей незалежно від конкретного змісту множин, що входять у них, і є підмножинами деякого універсуму  , тобто множинами з .Теорема. Для будь-яких множин  з булеану справедливі наступні тотожності (основні закони теорії множин):
Доведення (самостійно) всіх рівносильностей проводиться 1) за означенням рівності множин і за означеннями операцій над множинами. 2) за допомогою діаграм Ейлера-Венна. За допомогою основних властивостей операцій над множинами доводять рівності множин і спрощують вирази алгебри множин. 5. Декартовий добуток множин Нехай і – довільні множини. Означення. Впорядкованою парою називається пара  елементів  ,  , взятих в певному порядку.Дві впорядковані пари вважаються рівними, якщо рівні їх відповідні компоненти:  .Означення. Декартовим добутком двох множин і називається множина всіх впорядкованих пар : .Якщо  , то кажуть про декартовий квадрат множини : Аналогічно можна ввести декартовий добуток трьох 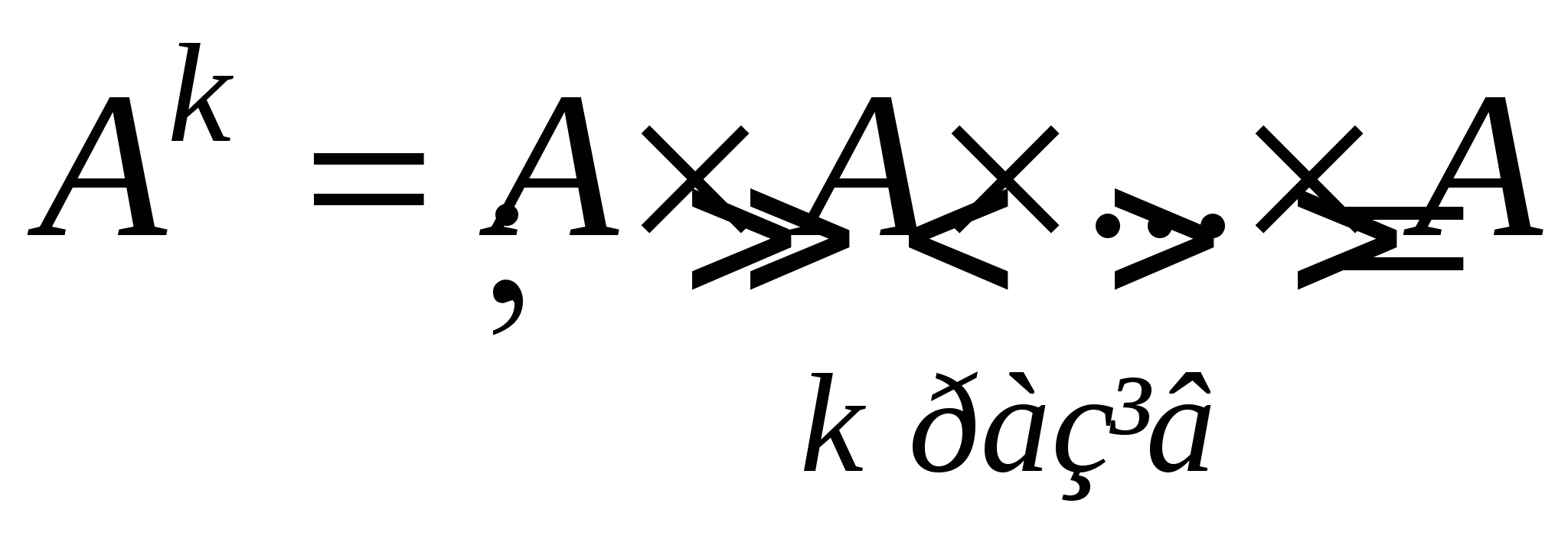 , чотирьох  і т.д. множин. При  скорочено пишуть  і кажуть про  -й декартовий степінь множини  . Елементами  є послідовності (набори, вектори, рядки)  довжини .За означенням покладають, що перший декартовий степінь будь-якої множини є сама множина , тобто  .Декартовий добуток має наступні властивості:
Приклад: Нехай  ,  . Тоді ; .2. Нехай R – множина всіх дійсних чисел. Тоді декартовий квадрат  є просто множина всіх декартових координат на площині відносно заданих координатних осей ( – множина точок площини). Якщо  , то  – одиничний квадрат на площині.Лекція розроблена доцентом кафедри ВМ, к.т.н. Скубаком О.М. | |||||||||||||||||||||||||||||||||||||||||||||||||||||
– комутативність 
– комутативність 
– 
– асоціативність
– дистрибутивність 
– дистрибутивність 
, 
– некомутативність;
– дистрибутивність відносно 
;
– дистрибутивність відносно 
;
.