Лекция 16. Цель лекции 16 Ознакомившись с лекцией 16 по теории электрических цепей студент должен знать
 Скачать 246.25 Kb. Скачать 246.25 Kb.
|
|
Электрические цепи с распределенными параметрами Лекция №16. Цель лекции №16: Ознакомившись с лекцией №16 по теории электрических цепей студент должен знать: Определение цепи с распределенными параметрами; Что такое первичные и вторичные параметры длинной линии; Уметь изображать и объяснять схему замещения участка цепи с распределенными параметрами; Телеграфные уравнения длинной линии; Условия, при которых длинная линия рассматривается как линия без потерь; Формулы коэффициента передачи и волнового сопротивления длинной линии; Что такое прямая и обратная волны? Формулы фазовой скорости и длины волны; Особенности согласованного и несогласованного режимов работы длинной линии; Когда возникает режим стоячих волн; Как определяется входное сопротивление линии4 Условие, при котором длинная линия является неискажающей; Условие, при котором длинная линия является линией без потерь; Уравнения длинной линии без потерь Формула волнового сопротивления линии без потерь. 16.1 ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ (ЦРП) 16.1.1 Введение Цепи с распределенными параметрами характеризуются протеканием в них волновых процессов, при которых переменные величины 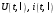 меняются не только во времени, но и в пространстве. При этом в любой фиксированный момент времени меняются не только во времени, но и в пространстве. При этом в любой фиксированный момент времени 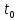 , значение напряжения (тока) может повторяться в пространстве через некоторый пространственный интервал , значение напряжения (тока) может повторяться в пространстве через некоторый пространственный интервал 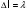 : :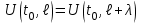 где 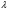 - длина волны. - длина волны.Если длина электрической цепи 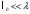 , то данную цепь можно считать цепью с сосредоточенными параметрами. В ЦРП длина электрической цепи соизмерима или больше длины волны. , то данную цепь можно считать цепью с сосредоточенными параметрами. В ЦРП длина электрической цепи соизмерима или больше длины волны.Примеры ЦРП : длинные линии электропередачи, линии телеграфной и телефонной связи. В ЦРП необходимо учитывать токи, обусловленные емкостями между проводами (токи смещения) и проводимостью изоляции (токи утечки через гирлянды изоляторов) и токи, обусловленные коронным электрическим разрядом вблизи поверхности проводов. Следовательно, ток в проводах не одинаков в разных сечениях линии. Ток в проводах линии вызывает падение напряжения в активном сопротивлении проводов и создает переменное магнитное поле, которое в свою очередь наводит вдоль всей линии ЭДС самоиндукции. Поэтому напряжение между проводами также не остается постоянным вдоль линии. Чтобы учесть изменения тока и напряжения вдоль линии, нужно считать, что каждый сколь угодно малый элемент линии обладает сопротивлением и индуктивностью, а между проводами – проводимостью и емкостью, т.е рассматривать линию как цепь с распределенными параметрами. Такую линию также называют длинной линией. 16.1.2. Первичные параметры ЦРП Свойства длинных линий определяются в первую очередь их распределенными параметрами. К ним относятся индуктивность и сопротивления проводов, а также емкость и проводимость утечки между проводами, которые распределены вдоль линии . К первичным параметрам длинной линии относятся: погонная индуктивность 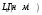 , погонная емкость , погонная емкость 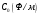 , погонное сопротивление потерь , погонное сопротивление потерь 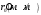 и погонное проводимость и погонное проводимость 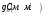 утечки. Как видно из рис.8.1. погонные параметры утечки. Как видно из рис.8.1. погонные параметры 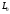 и и 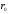 относятся не к двум, а к одному проводу длинной линии. относятся не к двум, а к одному проводу длинной линии.Определение первичных параметров ЦРП сопряжено, в частности, с расчетами электрических и магнитных полей. Если первичные параметры не изменяются вдоль линии, то ее называют однородной. Неоднородность линии может быть обусловлена, например, изменением расстояния между проводами двухпроводной линии.  Рисунок 16.1 Схема замещения длинной линии с указанием первичных параметров. 16.2 УРАВНЕНИЯ ОДНОРОДНОЙ ДВУХПРОВОДНОЙ ЛИНИИ В качестве ЦРП будем рассматривать двухпроводную линию, как типичный пример длинной линии. ЦРП можно представить виде множества соединенных в цепочку бесконечно малых элементов длинной 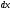 , каждый из которых имеет сопротивление , каждый из которых имеет сопротивление 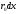 , и индуктивность , и индуктивность 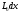 , проводимость , проводимость 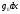 и емкость и емкость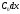 (рис.2). (рис.2).Дифференциальные уравнения длинной линии (рис 16.2): 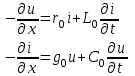 (16.1) (16.1)где  - расстояние от начала линии до текущего элемента ее длины; - расстояние от начала линии до текущего элемента ее длины; 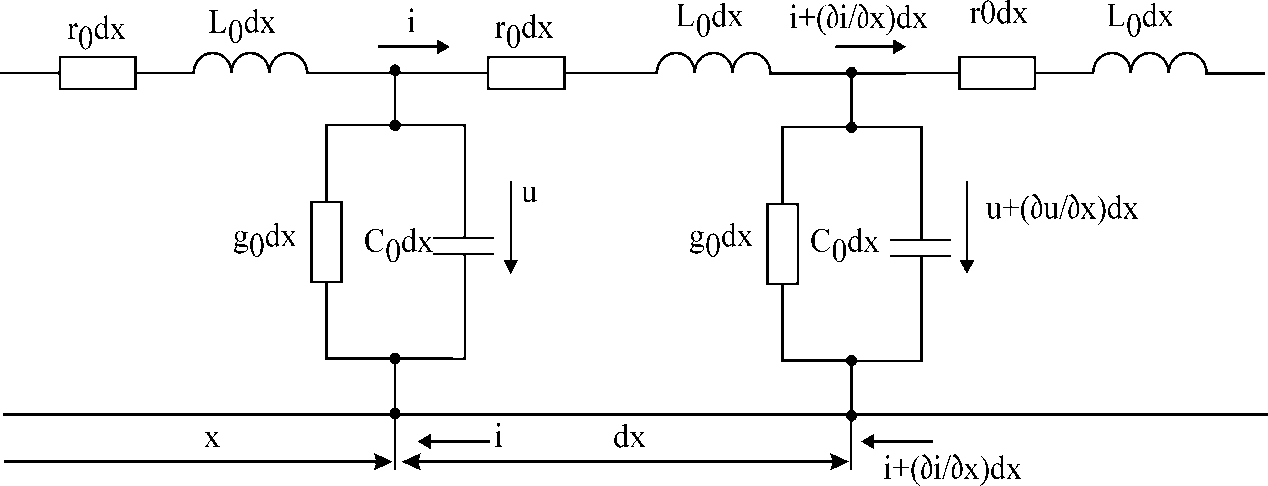 Рисунок 16.2 Схема замещения длинной линии 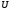 и и 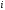 - мгновенные значения напряжения и тока в начале выбранного элемента линии - мгновенные значения напряжения и тока в начале выбранного элемента линии 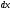 , , 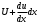 и и 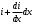 - мгновенные значения напряжения и тока в начале следующего элемента. - мгновенные значения напряжения и тока в начале следующего элемента.Система уравнений (8.1) дает возможность определить ток и напряжение, как функции расстояния от начала линии и времени. Эти уравнения справедливы при любых изменениях тока и напряжения. 16.2.1 Установившийся режим в однородной линии. Рассмотрим установившийся режим в длинной линии при синусоидальном напряжении источника питания. Переписывая уравнения (16.1) для установившегося режима и вводя комплексные напряжения, токи, сопротивления и проводимости, получаем 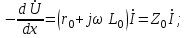 (16.2) (16.2)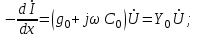 (16.3) (16.3)где 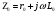 - комплексное сопротивление, - комплексное сопротивление, 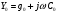 -комплексная проводимость линии единичной длины. Следует иметь ввиду, что -комплексная проводимость линии единичной длины. Следует иметь ввиду, что 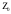 и и 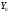 не являются величинами, обратными друг другу. не являются величинами, обратными друг другу.Уравнения (16.2), (16.3) называются телеграфными уравнениями. Они описывают закон изменения амплитуды и фазы гармонических колебаний вдоль линии. Для решения телеграфных уравнений продифференцируем уравнения (16.2), (16.3) по  и разделим в них переменные и разделим в них переменные 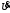 и и  . В результате получим: . В результате получим: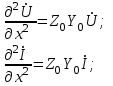 (16.4) (16.4)Перепишем эти уравнения в виде (16.5) 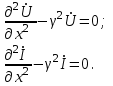 (16.5) (16.5)Здесь 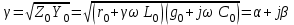 (16.6) (16.6)Уравнения (16.5) получили название волновых уравнений. 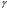 является комплексным параметром длинной линии и называется коэффициентом (постоянной) распространения волны. является комплексным параметром длинной линии и называется коэффициентом (постоянной) распространения волны. При 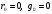 коэффициент распространения (16.7) является мнимой величиной: коэффициент распространения (16.7) является мнимой величиной: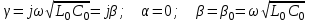 (16.7) (16.7)Длинная линия с параметром (8.7) называется линией без потерь. 16.2.2 Решение волновых (телеграфных) уравнений Для решения однородных волновых уравнений (16.5) составляем их характеристическое уравнение и определяем его корни: 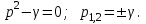 Отсюда получаем искомое решение: 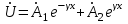 (16.8) (16.8)Где 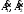 - комплексные постоянные интегрирования. - комплексные постоянные интегрирования.Ток согласно уравнению (16.3) 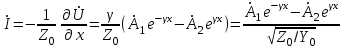 (16.9) (16.9)Знаменатель в уравнении 16.9, имеющий размерность сопротивления, называют волновым сопротивлением линии 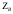 . . 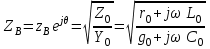 . (16.10) . (16.10)Коэффициент распространения 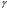 (16.7) и волновое сопротивление (16.7) и волновое сопротивление 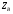 (16.10) называются вторичными параметрами однородной длинной линии. Эти параметры вполне определяют свойства линии как устройства для передачи энергии или информации. (16.10) называются вторичными параметрами однородной длинной линии. Эти параметры вполне определяют свойства линии как устройства для передачи энергии или информации.Учитывая, что комплексные постоянные интегрирования имеют вид: 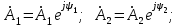 запишем мгновенные значения напряжения и тока : 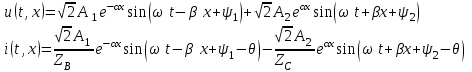 (16.11) (16.11)16.2.3 Прямая и обратная волны Для облегчения анализа процессов, происходящих в длинных линиях при установившемся синусоидальном режиме можно представить (16.11) условно как сумму прямых и обратных волн: 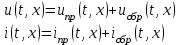 (16.12) (16.12)или 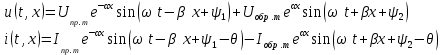 (16.13) (16.13)Прямую и обратные волны можно рассматривать как бегущие волны. Прямая волна движется от начала линии в сторону возрастания координаты, обратная волна движется от конца линии в сторону убывания координаты. Основными характеристиками бегущей волны является фазовая скорость и длина волны. Фазовой скоростью волны С называется скорость перемещения фазы колебания, которая в течении времени 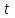 и по мере увеличения расстояния и по мере увеличения расстояния , пройденного волной, остается постоянной, т.е , пройденного волной, остается постоянной, т.е 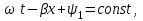 откуда следует, что 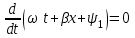 и 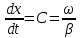 (16.14) (16.14)Наибольшая скорость движения волн в воздушной линии, потерями энергии в которой можно пренебречь. 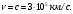 В кабеле фазовая скорость значительно меньше. В кабеле фазовая скорость значительно меньше.Длинной волны 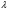 называется расстояние между ближайшими двумя точками, взятое в направлении распространении волны, фазы колебаний в которых различаются на называется расстояние между ближайшими двумя точками, взятое в направлении распространении волны, фазы колебаний в которых различаются на 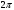 . Следовательно, для первого слагаемого (16.14) получим . Следовательно, для первого слагаемого (16.14) получим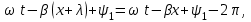 откуда 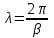 (16.15) (16.15)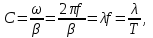 т.е за время равному периоду, волна пробегает расстояние, равное длине волны. 8.2.4 Уравнения однородной линии с гиперболическими функциями Для того, чтобы решить уравнение (16.8), (16.9), описывающие поведение длинных линий в установившемся режиме, необходимо определить постоянные интегрирования  Зададим граничные условия: напряжение Зададим граничные условия: напряжение 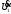 и ток и ток 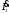 в начале линии в начале линии 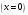 . Используя (16.8), (16.9) с граничными условиями находим . Используя (16.8), (16.9) с граничными условиями находим 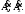 Подставляя найденные постоянные интегрирования Подставляя найденные постоянные интегрирования  в уравнения (16.8), (16.9), и вводя гиперболические функции в уравнения (16.8), (16.9), и вводя гиперболические функции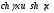 , получим , получим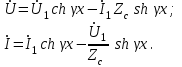 (16.16) (16.16)Здесь  -расстояние отсчитываемое от начала линии. Если требуется определить -расстояние отсчитываемое от начала линии. Если требуется определить  , ,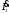 в любой точке линии, то расстояние удобно отсчитывать от конца линии. в любой точке линии, то расстояние удобно отсчитывать от конца линии.Обозначим 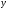 -расстояния, отсчитывание от конца линии. Тогда уравнения (16.16) примут вид -расстояния, отсчитывание от конца линии. Тогда уравнения (16.16) примут вид 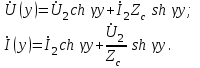 (16.17) (16.17)16.3 РЕЖИМЫ РАБОТЫ ДЛИННОЙ ЛИНИИ 16.3.1 Несогласованная нагрузка В однородной линии с генератором в начале и приемником в конце 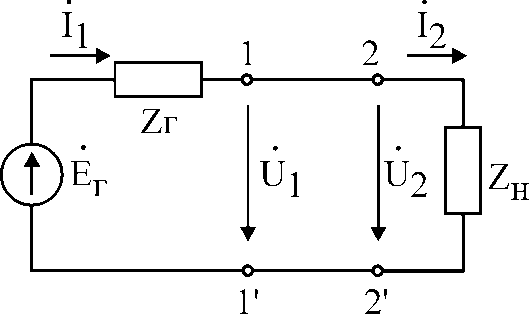 Рисунок 16.3 Работа длинной линии под нагрузкой. обратная волна возникает, когда нагрузка не согласованна: 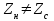 . .Отношения комплексного напряжения (тока) обратной волны в любой точке линии к комплексному напряжению (току) прямой волны называют коэффициентом отражения: 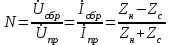 (16.18) (16.18)Наибольшее рассогласование получается при коротком замыкании и холостом ходе в конце линии. При коротком замыкании 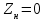 и и 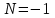 при холостом ходе при холостом ходе 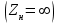 получаем получаем 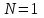 . При согласованной нагрузке . При согласованной нагрузке 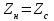 , , 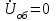 (обратной волны нет) и (обратной волны нет) и  Чем больше коэффициент отражения (по модулю), тем заметнее влияние обратной волны, тем менее равномерно распределяются напряжения и ток вдоль линии и яснее выражены максимумы и минимумы у кривой действующего значения напряжения (рис. 16.4) и тока. В случае несогласованной нагрузки не вся мощность, которую способна перенести прямая волна, поглощается сопротивлением нагрузки. С обратной волной часть мощности возвращается генератору.  Рисунок 16.4 Распределение действующего значения напряжения вдоль длинной линии при несогласованной нагрузке. Итак, обратная волна в однородной линии с генератором в начале и приемником в конце возникает при несогласованной нагрузке, когда  . Поэтому такую волну называют еще отраженной. Прямую волну в этом случае называют еще падающей. . Поэтому такую волну называют еще отраженной. Прямую волну в этом случае называют еще падающей. 16.3.2 Согласованная нагрузка Если сопротивление приемника равно волновому сопротивлению линии, т.е  то линия работает в режиме согласованной нагрузки. При этом уравнения линии (16.17) значительно упрощаются: то линия работает в режиме согласованной нагрузки. При этом уравнения линии (16.17) значительно упрощаются: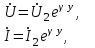 (16.19) (16.19)Из уравнений (16.19) видно, что при согласованной нагрузке обратная волна отсутствует. Действующие значения напряжения и тока из - за потерь в линии, как и в общем случае, не остаются постоянными. 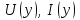 постепенно уменьшаются к концу линии (рис. 16.5). постепенно уменьшаются к концу линии (рис. 16.5).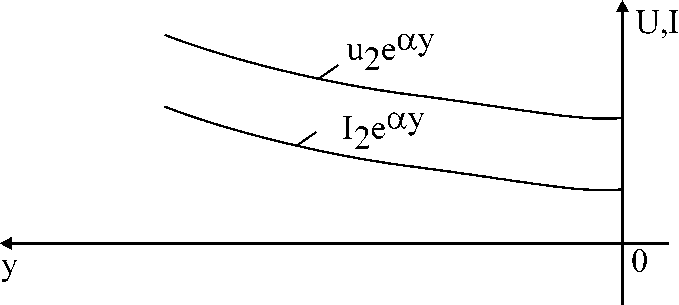 Рисунок 16.5 Распределение действующих значений тока и напряжения вдоль длинной линии с потерями. Мощность в любом сечении линии 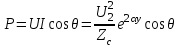 Здесь 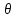 - угол сдвига фаз между напряжением и током. - угол сдвига фаз между напряжением и током.Эта мощность уменьшается по мере удаления от начала линии, так как на каждом элементе длины линии 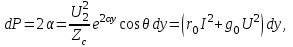 Мощность потерь равна сумме потерь в сопротивлении проводов и в проводимости изоляции на элементе линии 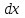 . . При согласованной нагрузке вся мощность волны, достигшей конца линии, поглощается в нагрузке. Обратной волны нет, что во многих случаях передачи информации важно для нормальной работы передающей и передающей и приемной аппаратуры. Поэтому согласование нагрузки одна из главных задач, которую приходится решать при организации передачи информации. 16.4 ВХОДНОЕ СОПРОТИВЛЕНИЕ ЛИНИИ Под входным сопротивлением линии 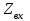 понимают сопротивление двухполюсника, которым можно заменить линию вместе с приемником на ее конце при расчете режима в начале линии. понимают сопротивление двухполюсника, которым можно заменить линию вместе с приемником на ее конце при расчете режима в начале линии.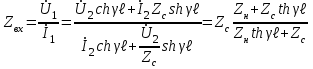 (16.20) (16.20)Это выражение показывает, что входное сопротивление линии зависит как от параметров линии и ее длины, так и от сопротивления нагрузки в конце линии. Входное сопротивление линии 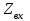 , а также вторичные параметры линии , а также вторичные параметры линии 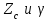 могут быть выражены, используя режимы холостого хода и короткого замыкания. могут быть выражены, используя режимы холостого хода и короткого замыкания.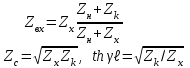 (16.21) (16.21)Здесь 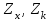 - входные сопротивления линии при холостом ходе и коротком замыкании. Эти величины могут быть определены как теоретически, так и экспериментально из опытов холостого хода и короткого замыкания линии. - входные сопротивления линии при холостом ходе и коротком замыкании. Эти величины могут быть определены как теоретически, так и экспериментально из опытов холостого хода и короткого замыкания линии.16.5 ЛИНИЯ БЕЗ ИСКАЖЕНИЙ Если сигналы, передаваемые по линиям связи, телеуправления и т.п. являются несинусоидальным, но периодическими их можно разложить в тригонометрические ряды с помощью преобразования Фурье (дискретные спектры). Если сигналы несинусоидальные и непериодические (например, сигналы, соответствующие передаваемой музыке, речи), то их можно разложить в непрерывный спектр. Тогда анализ прохождения сигналов по линиям, можно проводить, анализируя прохождение отдельных гармоник. Сигналы, передаваемые по линии, искажаются, если различны затухание и фазовая скорость отдельных гармонических составляющих сигнала. Для устранения амплитудных искажений необходимо добиться постоянства коэффициента затухания 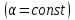 т.е постоянной амплитудной характеристики линии. Фазовые искажения отсутствуют при постоянной фазовой скорости т.е постоянной амплитудной характеристики линии. Фазовые искажения отсутствуют при постоянной фазовой скорости 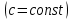 т.е. линейной зависимости коэффициента фазы от частоты т.е. линейной зависимости коэффициента фазы от частоты 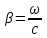 или, короче говоря, линейной фазовой характеристики линии. или, короче говоря, линейной фазовой характеристики линии.Линия является неискажающей, если выполняется условие 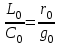 или или 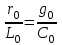 (16.22) (16.22)При выполнении условия (25), т.е для неискажающей линии 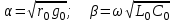 (16.23) (16.23)Фазовая скорость будет определятся как 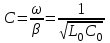 (16.24) (16.24)Волновое сопротивление такой линии чисто активное и не зависит от частоты. 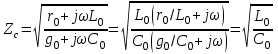 (16.25) (16.25)Большинство линий передачи информации не относятся к типу неискажающих. Искажение сигналов в ряде случаев устраняют при помощи специальных корректирующих устройств сразу для всего тракта передачи сигналов, который состоит не только из линии, но и фильтров, усилителей, трансформаторов и других устройств. Неискажающая линия является одновременно и линией с минимально возможным затуханием при заданных параметрах 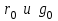 . .16.6 ЛИНИЯ БЕЗ ПОТЕРЬ Потери в линии отсутствуют, если 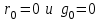 . Практически это значит, что активным сопротивлением проводов можно пренебречь по сравнению с индуктивным и активной проводимостью между проводами по сравнению с емкостной. Такую линию называют линией без потерь. . Практически это значит, что активным сопротивлением проводов можно пренебречь по сравнению с индуктивным и активной проводимостью между проводами по сравнению с емкостной. Такую линию называют линией без потерь. Для высокочастотных коротких линий, применяемых в радиотехнике, часто с достаточно большой точностью можно пренебречь сопротивлением 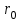 и утечкой и утечкой 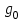 по сравнению с по сравнению с 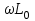 и и 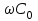 . .У линии без потерь волновое сопротивление чисто активное и не зависит от частоты 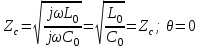 (16.26) (16.26)Коэффициент затухания равен нулю 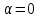 (16.27) (16.27)а коэффициент фазы пропорционален частоте 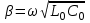 (16.28) (16.28)Фазовая скорость в линии без потерь постоянна 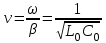 (16.29) (16.29)Следовательно, линия без потерь не искажает сигналов. Фазовая скорость в воздушной линии совпадает со скоростью электронных волн в вакууме ( воздухе), т.е. наибольшая 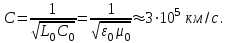 (16.30) (16.30)Здесь 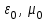 -электрическая и магнитная постоянные -электрическая и магнитная постоянные Для кабеля фазовая скорость равна скорости электромагнитных волн в диэлектрике, т.е. меньше скорости света в вакууме в 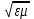 раз ( раз (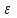 -диэлектрическая проницаемость, -диэлектрическая проницаемость, 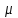 -магнитная проницаемость) -магнитная проницаемость)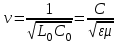 (16.31) (16.31)Уравнения однородной линии с гиперболическими функциями от комплексного аргумента заменяются для линии без потерь уравнениями с круговыми функциями от вещественного аргумента. Если заданы 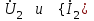 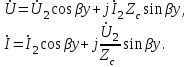 (16.32) (16.32)Если заданы 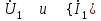 то получим то получим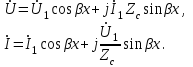 (16.33) (16.33)Напряжение и токи в линии без потерь, как и в общем случае, можно представить в виде двух волн: прямой и обратной. Только амплитуда каждой волны остается постоянной вдоль всей линии, т.к. потерь энергии нет 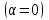 . Напряжение и ток каждой волны совпадают по фазе, т.к. волновое сопротивление часто активное . Напряжение и ток каждой волны совпадают по фазе, т.к. волновое сопротивление часто активное 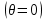 . .Входное сопротивление линии без потерь 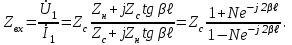 (16.34) (16.34)16.6.1 Согласованная нагрузка линии без потерь При согласованной (активной) нагрузке 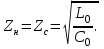 Используя (16.33), учитывая, что Используя (16.33), учитывая, что 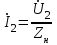 , получим , получим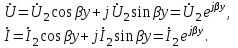 (16.35) (16.35)Из (16.35) видно, что действующие значения напряжения и тока в произвольном сечении линии одинаковые и не зависят от расстояния 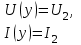 (16.36) (16.36)Обратных (отраженных) волн нет ( 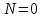 ), в линии присутствуют ), в линии присутствуют прямые (бегущие) волны (рис. 16.6). 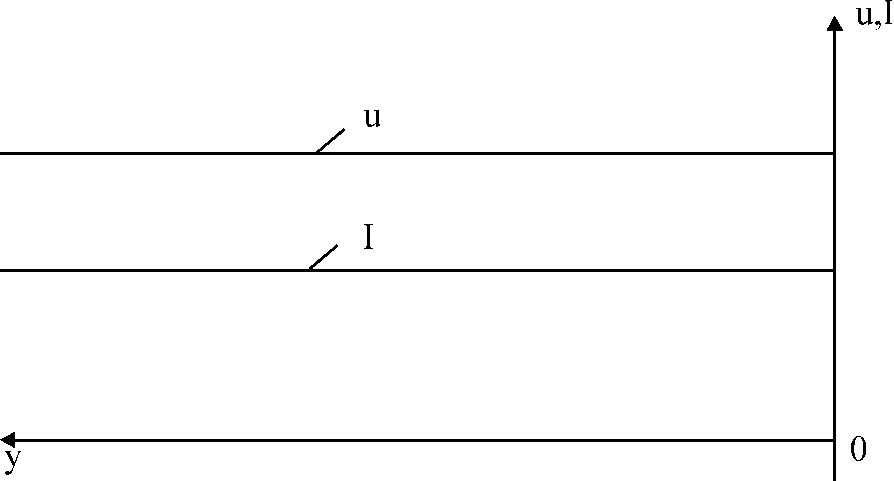 Рисунок 16.6 Распределение действующих значений напряжения и тока в линии без потерь. 16.6.2 Стоячие волны Чем значительней отличается сопротивление нагрузки 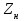 от волнового сопротивления от волнового сопротивления 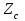 , тем заметнее становится отраженная волна. , тем заметнее становится отраженная волна.Рассмотрим режимы, при которых активная мощность в конце линии без потерь равна нулю. Эта может быть при: Холостом ходе, Коротком замыкании, Часто реактивной нагрузке. В этих случаях падающая волна полностью отражается от конца линии (от нагрузки). При холостом ходе 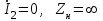 из (16.35) следует из (16.35) следует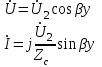 (16.37) (16.37)Мгновенные значения напряжения и тока 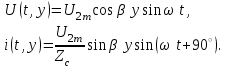 (16.38) (16.38)Уравнение (16.38) представляет собой уравнение стоячих волн. Стоячей волной называется процесс, получающийся от наложения прямой и обратной волн с одинаковыми амплитудами. 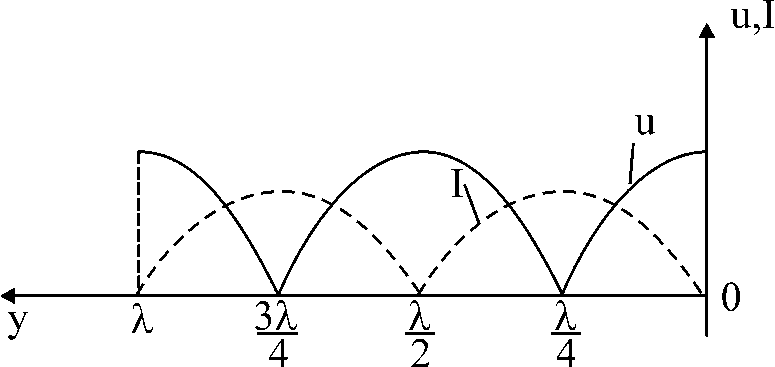 Распределение действующих значений напряжения и тока вдоль линии при холостом ходе показано на рис. 16.7. Рисунок 16.7 Распределение действующих значений напряжения и тока вдоль линии при холостом ходе Максимальные значения напряжения и тока называют пучностями, нули напряжения и тока – узлами. Узлы и пучности напряжения и тока неподвижны. Узлы тока совпадают с пучностями напряжения и наоборот. При коротком замыкании линии 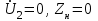 из (8.35) из (8.35)следует 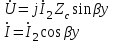 (16.39) (16.39)Напряжение и ток опять образуют стоячие волны. Из (16.39) определим распределение действующих значений напряжения и тока вдоль линии 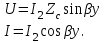 (16.40) (16.40)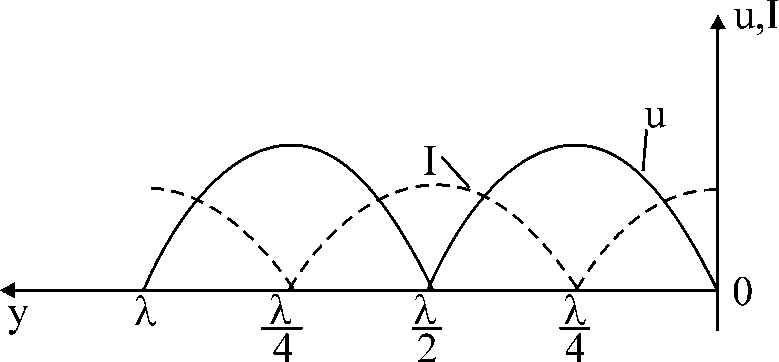 Рисунок 16.8 Распределение действующих значений напряжения и тока вдоль линии при коротком замыкании Графики действующих значений 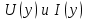 приведены на рис.16.8. приведены на рис.16.8.Сдвиг по фазе между напряжением и током в любой точке линии по прежнему составляет 900. В линии с чисто реактивной (индуктивной или активной) нагрузкой также возникают стоячие волны, так как линия без потерь с реактивной нагрузкой не поглощает энергии. Поэтому амплитуда отраженной волны равна амплитуде падающей. Емкостное и индуктивное сопротивления можно заменить отрезком короткозамкнутой или разомкнутой линии. Действительно, входное сопротивление короткозамкнутой или разомкнутой линии без потерь в зависимости от ее длины имеет индуктивный или емкостный характер, причем величина входного сопротивления изменяется от нуля до бесконечности. Всегда длину отрезка короткозамкнутой или разомкнутой линии можно подобрать так, чтобы его входное сопротивление равнялось сопротивлению нагрузки. Например, длина отрезка короткозамкнутой линии 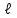 , которым можно заменить индуктивность , которым можно заменить индуктивность 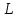 , определится из уравнения : , определится из уравнения :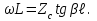 Здесь 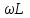 -сопротивление индуктивной нагрузки; -сопротивление индуктивной нагрузки; 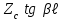 - входное сопротивление отрезка короткозамкнутой линии (получено из общего выражения для входного сопротивления линии без потерь). - входное сопротивление отрезка короткозамкнутой линии (получено из общего выражения для входного сопротивления линии без потерь).Если индуктивность 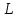 , заменить отрезком разомкнутой линии, то его длина , заменить отрезком разомкнутой линии, то его длина 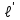 определится из уравнения определится из уравнения 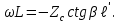 Аналогично можно получить формулы для определения длины отрезка короткозамкнутой или разомкнутой линии при замене им емкостной нагрузки. 16.6.3 Произвольная нагрузка линии без потерь Рассмотрим режим линии без потерь при произвольном сопротивлении нагрузки 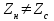 . .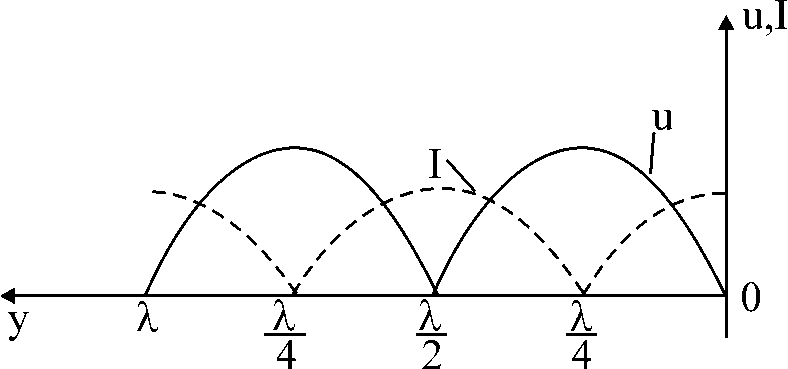 В этом случае, как при холостом ходе и коротком замыкании, напряжение и ток в любой точке линии можно представить состоящими из двух волн (прямой и обратной). Но при этом действующие значения напряжения и тока обратной волны не равны действующим значениям напряжения и тока прямой волны. Рисунок 16.9 Распределение действующих значений напряжения и тока вдоль линии при произвольной нагрузке. Отношение минимального напряжения к максимальному оценивает степень согласования нагрузки и называется коэффициентом бегущей волны . 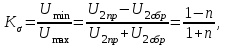 где 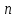 - модуль коэффициента отражения - модуль коэффициента отражения Обратную величину называют коэффициентом стоячей волны 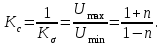 Коэффициент бегущей волны в зависимости от согласованности нагрузки может принимать значения от 0 ( 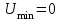 при холостом ходе и коротком замыкании) до 1 ( при холостом ходе и коротком замыкании) до 1 (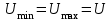 при согласованной нагрузке ). Соответственно коэффициент стоячей волны изменяется в пределах от при согласованной нагрузке ). Соответственно коэффициент стоячей волны изменяется в пределах от  до 1. до 1. |
