Лекция. Лекция 20. Лекция 20 Основы динамики сооружений Учебные вопросы 20 Предмет и задачи динамики сооружений

• Название: Лекция 20 Основы динамики сооружений Учебные вопросы 20 Предмет и задачи динамики сооружений
• Анкор: Лекция
• Дата: 18.09.2021
• Размер: 0.5 Mb.
• Имя файла: Лекция 20.doc
• Тип: Лекция; #233757
• страница: 3 из 3

Рис.14.7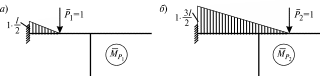


Рис.14.8
Коэффициенты и находим перемножением эпюр и по формуле Мора.

Здесь определяется как результат перемножения эпюры (рис.14.7, б) самой на себя, как результат перемножения эпюры (рис.14.7, б) с (рис.14.8, а).

(14.45)

С учетом (14.45) из решения (14.44) получим:

.

Эпюра изгибающих моментов в заданной системе от действия сил Р₁ =1 и Х₁ = 5/16 изображена на рис.14.9, a.



Рис.14.9

Рассчитываем раму на действие силы Р₂ = 1. Каноническое уравнение метода сил в данном случае принимает вид:

. (14.46)

Здесь определяется как результат перемножения эпюры моментов, изображенных на рис.14.7, б и 14.8, б, в соответствии с формулой Мора:

. (14.47)

С учетом значения из (14.45) и значения из (14.47) и из (14.46) получим:

.

Эпюра изгибающих моментов от действия сил Р₂ = 1 и Х₁ = = 7/4 в заданной системе изображена на рис.14.9, б.

Единичное перемещение определяется по формуле Мора в результате перемножения эпюры самой на себя, применяя формулы умножения двух эпюр моментов в виде двух трапеций на произвольном участке. Получим:



м/кН.

Единичное перемещение определяется по формуле Мора перемножением эпюры самой на себя (рис.14.9, б):



м/кН.

Единичное перемещение определяется по формуле Мора в результате перемножения эпюр и , изображенных соот­ветственно на рис.14.9, а, б:



м/кН.

Решив уравнение (14.40), получим:

,

откуда

.

Окончательно =166,75×10^-6 м/кН; =10,.35×10^-6 м/кН.

По формуле (14.41) определяется значение собственной частоты рассматриваемой рамы:

c^-1;

c^-1.

Периоды собственных колебаний рассматриваемой системы принимают значения: c; c. 

2. Определение амплитуды собственных колебаний и графическое изображение собственных форм

Для вычисления значения отношений амплитуды собственных колебаний из (14.42), предварительно определив кН∙с²/м, имеем при = 1 и при = 1, соответственно:





Формы собственных колебаний рассматриваемой системы изо­бражены на рис.14.10 (а - первая форма; б - вторая форма).

3. Проверка ортогональности собственных форм колебаний

Из условия ортогональности (14.43) имеем:

.


Рис.14.10
4. Определение круговой частоты вынужденных колебаний и изображение примерного вида графика коэффициента динамичности в зависимости от отношения частот вынужденных и собственных колебаний

В стационарном режиме круговая частота вынужденных колеба­ний системы имеет значение:

 c^-1.

Сопоставим величину с величиной ближайшей собственной частоты рамы :

.

Во избежание резонансных колебаний надо изменить величину или . В данном случае, принимая n = 900 об/мин, получим:

 c^-1;

,



Рис.14.11
Следовательно, при  с^-1 при­нятое условие во избежание резонансных колебаний выполняется.

Примерный вид графика коэффици­ента динамичности в зависимости от изображен на рис. 14.11.

5. Определение амплитудных значений инерционных сил

В соответствии с принятым обозначением по формулам (14.34) и (14.35) последовательно определяем:

м/кН;

м/кН;

кН;

м/кН;

м/кН;

м²/кН;

м²/кН;

м²/кН.

По (14.33) определяем амплитудные значения инерционных сил:

= |D₁/D |= |3,72/0.5| = 7,44 кН;

= |D₂/D |= |9,64/0.5 |= 19,28 кН.

6. Определение эпюры изгибающих моментов от действия собственного веса вибраторов и амплитудных значений изгибающих моментов при вынужденном стационарном режиме колебания рамы

Значение изгибающих моментов, возникающих от действия собственного веса вибраторов, в произвольном сечении опреде­ляется по формуле:

.

Определяем значение в характерных сечениях (0; 1; 2; 3) рамы (см. рис.14.9):

сечение 0: = 20×(9/8 - 3/2) = -7,5 кН×м;

сечение 1: = 20×(-15/16 + 3/4) = -3,75 кН×м;

сечение 2: = 0;

сечение 3: = 20×(0 + 3) = 60 кН×м.

Эпюра изгибающих моментов приведена на рис.14.12.

Амплитудные значения изгибающих моментов от действия внешних динамических и инерци­онных нагрузок в соответствии с (14.37) определяются:

= 

.



Рис. 14.12
Согласно последней формуле в характерных сечениях имеет

следующие значения:

сечение 0:  кН×м;

сечение 1:   кН×м;

сечение 2: = 0;

сечение 3:   кН×м.

Эпюра изображена на рис.14.12 (пунктиром).

7. Построить эпюру моментов при одновременном действии статических и динамических сил и определить положение опасного сечения конструкции

Результирующее значение изгибающих моментов, действующих в характерных сечениях при одновременном действии статических и динамических нагрузок, определяется по формуле:

.

Эпюра M_k, как и эпюры и , изображены на рис.14.12.

Из рис.14.12 согласно эпюре М следует, что наиболее опасным яв­ляется сечение 3.

8. Определение максимального напряжения и проверка условий прочности в наиболее опасном сечении

кН/м² = 53,2МПа <R = 190 МПа.

Следовательно, условие прочности рассматриваемой рамы обес­печено.
НАЗАД                      НА ОГЛАВЛЕНИЕ                   ДАЛЕЕ



Главная / Лекции / Расчетно-графические работы / Расчеты строительных конструкций на ЭВМ / Зачетные вопросы / Справочные данные / Литература
14.7. Поперечные колебания балки с распределенными параметрами


Рис.14.13

Рассмотрим свободные колеба­ния балки с постоянным попе­речным сечением площадью F, плотностью r материала конструк­ции, без учета диссипативных свойств системы (рис.14,13,  а).

Дифференциальное уравнение колебания системы с учетом сле­дующего дифференциального соот­ношения теории изгиба имеет вид:

. (14.48)

Здесь  - распределенная инерционная нагрузка, которая воз­никает при движении балки:

, (14.49)

где -  распределенная масса балки.

Совместно рассматривая соотношения (14.48) и (14.49), получим дифференциальное уравнение свободных колебаний балки без учета диссипативных свойств системы:

. (14.50)

Если учесть затухания колебания по Фойгту в вынужденном ре­жиме при действии внешней нагрузки P(z,t) на балку, дифферен­циальное уравнение (14.50) преобразуется в виде:

, (14.51)

т.е. для исследования вынужденного движения балки необходимо рассмотреть решение уравнения (14.51), при заданных граничных условиях закрепления балки и начальных условиях задачи.

Рассмотрим решение задачи в свободном режиме колебания.

Для решения задачи применим метод разделения переменных, т.е.:

. (14.52)

Подставляя решение (14.52) в уравнение (14.50) и, принимая обо­значения

, (14.53)

получим:

(14.54)

Решение последнего уравнения запишем в общем виде:

. (14.55)

Произвольные постоянные C_i (i = 1,2,3,4) должны быть опреде­лены из граничных условий закрепления балки.

Предположим, что рассматриваемая балка закреплена в обоих концах шарнирно. Тогда на каждой опоре прогиб y и изгибающий момент обращаются в нуль, следовательно, учитывая решение (14.55), имеем:

   .

Из первых двух условий вытекает, что C₂ = C₄ = 0. Из двух дру­гих получим:



Приравниваем нулю определитель этой системы:

,

откуда имеем .

Но так как, гиперболический синус обращается в нуль только при = 0, то остается  = 0 или  (i = 1,2,...), или соглас­но (14.53) выражение частоты собственных колебаний принимает вид:

. (14.56)

В зависимости от значения i = 1,2,... по формуле (14.56) опреде­ляется спектр частот собственных колебаний соответствующий соб­ственным формам, показанным на рис.14.13, б, в, г. Упругая линия балки, учитывая, что C₂ = C₃ = C₄ = 0, при i-ой форме колебаний имеет вид:

.

Окончательная формула по определению прогиба балки, соглас­но (14.52), записывается в виде:

,

здесь C₁- определяется из начальных условий задачи, в зависи­мости от способа возбуждения колебаний балки.
14.8. Определение основной частоты собственных

колебаний консольной балки



Рис.14.14

Требуется определить основную частоту собственных колебаний консольной балки с постоянным поперечным сече­нием (рис.14.14).

Для определения функции Z в данном случае имеем следующие граничные условия:



откуда получим:

(14.57)

Подставляя выражение (14.55) в граничные условия (14.57), будем иметь:

;



;

.

Приравнивая нулю определитель этой системы, получим:



отсюда имеем .

Наименьший корень этого трансцендентного уравнения прини­мает значение: .

Учитывая соотношение (14.53), находим частоту основного (наи­меньшего) тона колебаний:

.

НАЗАД                      НА ОГЛАВЛЕНИЕ                   ДАЛЕЕ