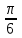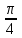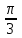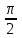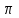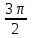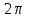Лекция 22. Радианная мера дуг и углов. Лекция 22. Тема урока Радианная мера углов. Цели урока 1 учебные
 Скачать 0.67 Mb. Скачать 0.67 Mb.
|
1 2 Лекция 22. Тема урока: «Радианная мера углов». Цели урока: 1) учебные: дать понятие о радианном измерении углов, изучить связь между градусной и радианной мерами измерения углов, познакомиться с формулами перевода градусной меры в радианную меру и наоборот, получить представление о вычисление длины дуги с использование значений углов в радианах, научиться применять формулы, изученные на уроке для решения задач и упражнений. 2) развивающие: получение учащимися представлений о появлении тригонометрии как науки, о её практическом применении, развитие навыков абстрактного мышления, развитие представлений о разностороннем подходе к решению задач, воспитывающие: активизировать интерес к изучаемому материалу. Ход урока. 1.Организационный момент. Проверка готовности к уроку. 2. Мотивация урока. Проверяется подготовленность классного помещения и готовность учащихся к уроку. Сегодня у нас первый урок нового для нас раздела математики – тригонометрии. С отдельными тригонометрическими понятиями вы уже могли встречаться на уроках геометрии и алгебры в 8-9 классах. Но полноценное знакомство с этой наукой мы начинаем именно сегодня. В древности люди следили за светилами и по этим наблюдениям вели календарь, рассчитывали сроки сева, время разлива рек; корабли на море, караваны на суше ориентировались в пути по звездам. Все это привело к потребности научиться вычислять стороны в треугольнике, две вершины которого находятся на земле, а третья представляется точкой на звездном небе. Исходя из этой потребности и возникла наука – тригонометрия – наука, изучающая связи между сторонами в треугольнике. Как вы думаете, достаточно ли уже известных нам соотношений для решения таких задач? Цель сегодняшнего урока – исследовать новые связи и зависимости, вывести соотношения, применяя которые на следующих уроках геометрии, вы сможете такие задачи решать. Давайте почувствуем себя в роли научных работников и вслед за гениями древности Фалесом, Евклидом, Пифагором пройдем путь поиска истины. Для этого нам нужна теоретическая база. 3. Актуализация опорных знаний. Проверка д/з. Что называется углом? виды углов, единицы измерения. Транспортир. Построение углов. 1°= 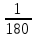 часть развернутого угла. часть развернутого угла.Синусом острого угла прямоугольного треугольника называется… отношение противолежащего катета к гипотенузе. Косинусом острого угла прямоугольного треугольника называется… отношение прилежащего катета к гипотенузе. Тангенсом острого угла прямоугольного треугольника называется… отношение противолежащего катета к прилежащему катету. 4. Изучение нового материала. Просмотр презентации. Творческое задание. В тригонометрии угол-это фигура, образованная при повороте луча на плоскости около начальной точки. Работа с учебником с.234. Измерение углов. Каждому углу как фигуре ставится в соответствие угол поворота, с помощью которого образован этот угол. Направление поворота против часовой стрелки положительное, а по часовой стрелке - отрицательное. Выполнить задание 1 (нечетные) с.238. В математике и физике. Кроме градусной меры углов. Используется радианная мера. Углом в один радиан называют центральный угол, которому соответствует длина дуги, равная длине радиуса окружности. 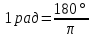 ; ; 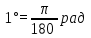 ; ; 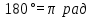 ; ; 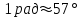 Переход от градусной меры углов к радианной Найдём радианную меру угла72 ° Так как 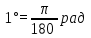 , то , то 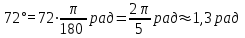 При записи радианной меры угла, обозначение «рад» часто опускают. Например: 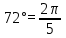 . .Заполнить таблицу:
Переход от радианной меры углов к градусной Выразим в градусах 4,5 рад. Так как 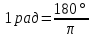 , то , то 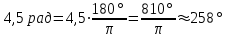 Историческая пауза. В IV-V веках появился уже специальный термин в трудах по астрономии великого индийского учёного Ариабхаты, именем которого назван первый индийский спутник Земли. Дугу он назвал ардхаджива (ардха – половина, джива – тетива лука, которую напоминает хорда). Позднее появилось более краткое название джива. Арабскими математиками в IX веке это слово было заменено на арабское слово джайб (выпуклость). При переводе арабских математических текстов в веке оно было заменено латинским синус (sinus – изгиб, кривизна). Слово косинус намного моложе. Косинус – это сокращение латинского выражения completely sinus, т. е. “дополнительный синус” (или иначе “синус дополнительной дуги”; cosa = sin( 90° - a)). Название «тангенс», происходящее от латинского tanger (касаться), появилось в 1583 г. Tangens переводится как «касающийся» (линия тангенсов – касательная к единичной окружности). Термин «тригонометрия» означает дословно треугольникомерие или измерения в треугольнике. 5. Закрепление нового материала. Решение у доски: пример 1, 2 с.236, 2, 4 (нечетные) 6. Повторение. Понятие множества. Решить №1. 2 с.14 Логическое задание. 7. Самостоятельная работа. Вариант 1. Выразите в радианной мере величины углов 75º и 168º. Выразите в градусной мере величины углов 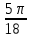 и и 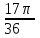 . .Вариант 2. Выразите в радианной мере величины углов 64º и 160º. Выразите в градусной мере величины углов 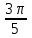 и и 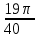 . .8.Итоги урока. Рефлексия. Д\З. Выучить п.16, повторить п.1 Решить: На 7 баллов: № 1(четные), 3 на 9 баллов: +№ 4 (четные) на 12 баллов: +№ 5 (п.1) Сообщение: «Такие разные углы»». Наше занятие подходит концу. Пожалуйста, поделитесь с нами своими мыслями о сегодняшнем занятии (хотите одним предложением). Вам для этого помогут слова: -Я узнал… -Я почувствовал… -Я увидел… -Я сначала испугался, а потом… -Я заметил, что … «Сенкан» к слову «Угол». Урок по теме «Свойства тригонометрических функций» Цель урока: Образовательные: Изучить свойства тригонометрических функций, закрепить изученный материал при решении упражнений; Развивающие: развивать умения, анализировать, применять имеющиеся знания у учащихся в изменённой ситуации. Воспитательные: воспитывать у учащихся аккуратность, любознательность, бережное отношение к окружающему миру, нравственные качества; создать условия для развития познавательной активности учащихся, реализации личностных функций каждого учащегося. Ход урок: 1. Организационный момент Притча о цели. 2. Мотивация урока. Сегодняшний урок мне хотелось бы начать со слов великого ученого-физиолога И.П Павлова: «Изучите азы науки, прежде чем взойти на ее вершины. Никогда не беритесь за последующее, не усвоив предыдущее». С Мы живем в реальном мире и для его познания нам необходимы знания. Но прежде, чем подняться на следующую ступеньку, нужно убедиться, что мы крепко стоим на ногах, имеем хорошие, прочные знания по изучаемой теме. Скажите, пожалуйста, какую тему мы изучаем? А всякое знание должно перейти в умение и навык. 3. Актуализация опорных знаний. Проверка д/з. Какие могут быть углы? Как называются стороны прямоугольного треугольника? Что такое катет? Что такое гипотенуза? Какие соотношения между сторонами и углами этого треугольника вы знаете? Синусом острого угла прямоугольного треугольника называется… отношение противолежащего катета к гипотенузе. Косинусом острого угла прямоугольного треугольника называется… отношение прилежащего катета к гипотенузе. Тангенсом острого угла прямоугольного треугольника называется… отношение противолежащего катета к прилежащему катету. Устный счет по «Ромашке» (На лепестках «Ромашки» написаны значения углов в радианах. В центр поочередно прикрепляются таблички «cos» ,«sin», «tg».) Лепестки «Ромашки»: 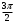 , , 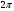 , ,  , , 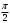 , 0, , 0, 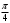 , , 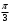 , , 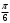 . .Сердцевинки «Ромашки»: «cos», «sin», «tg». Углом в один радиан называют центральный угол, которому соответствует длина дуги, равная длине радиуса окружности. 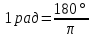 ; ; 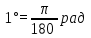 ; ; 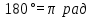 ; ; 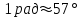 Переход от градусной меры углов к радианной Переход от радианной меры углов к градусной С/Р:
Задание. В какой координатной четверти расположены углы: 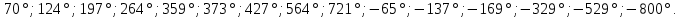 4.Изучение нового материала. -Знаки тригонометрических функций: 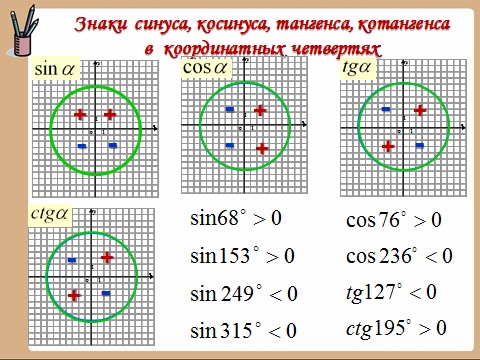 Задание. Определить знак. 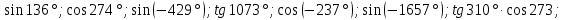 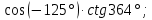 Определите знак 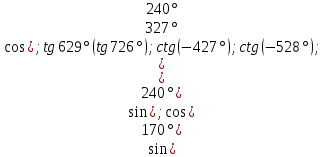 -Четность и нечетность функций: По единичной окружности устанавливаем равенства: Получаем Вывод: -Периодичность функции: Еще одним из пунктов исследования функции является исследование функции на периодичность. Функция называется периодичной, если существует такое число T, что для любого значения х из области определения функции Число T называют периодом функции. Например, известные нам тригонометрические функции являются периодическими, наименьший положительный период функций y=sinxи y=cosx равен 2П, y=tgxиy=ctgx , наименьший положительный период которых равен П. Работа с таблицей 278 учебника. 5. Зарядка для глаз. 6.Закрепление нового материала. Решить №__________________ 7.Самостоятельная работа с учеником с.245-249. Разобрать примеры с решениями с.249-250. Задание на повторение. 8.Итоги урока. Рефлексия. Д/з. Выучить п.__, вопросы с._____. Сообщение « Из истории тригонометрии». Решить №______________ Что вы узнали нового? На уроке: вы рассматривали … вы анализировали … вы получили … вы сделали вывод … вы пополнили словарный запас следующими терминами … 1 2 |