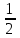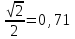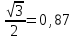Лекция 22. Радианная мера дуг и углов. Лекция 22. Тема урока Радианная мера углов. Цели урока 1 учебные
 Скачать 0.67 Mb. Скачать 0.67 Mb.
|
1 2 Цели урока: Ознакомить учащихся со свойствами функции у=sin x и у=соs x, обучение построению графика функции у=sin x и у=соs x, чтению этого графика, использование свойств и графика функции у=sin x и у=соs x, при решении неравенств. Задачи урока. Образовательные – формировать умение построения графика функции у= sinx, рассмотреть свойства графика, формировать навыки свободного чтения графиков, умение считывать свойства функции по графику. Развивающые – развивать логическое мышление, умение анализировать, обобщать полученные знания. Воспитательные – активизировать интерес к получению новых знаний, воспитывать графическую культуру, формировать точность и аккуратность при выполнении чертежей. Ход урока 1. Организационный момент. Приветствие. 2. Объявление темы и цели урока. Тема урока: «Свойства функции у=sin x и ее график». Сегодня рассмотрим свойства функции у=sinx и построим график. Рассмотрим простейшие преобразования функции, построим графики этих функций и перечислим их свойства. 3 Актуализация опорных знаний: Выполнение устных упражнений. Повторить определение тригонометрических функций и знаки значений этих функций. Затем учащиеся отвечают на вопросы: Учащимся предложена иллюстрация единичной окружности. Вопросы: При каких значениях х функция у=sinx принимает значение, равное 0? 1? -1? Может ли функция у=sinx принимать значение больше 1, меньше -1? При каких значениях х функция у=sinx принимает наибольшее (наименьшее) значение? Каково множество значений функции у=sinx? Дана иллюстрация единичной окружности. Повторив знаки значений тригонометрических функций в каждой четверти координатной плоскости, учащимся предлагается показать несколько точек единичной окружности, соответствующих числам, синус которых положительное (отрицательное) число. Затем ответить на вопросы: Какой знак имеет значение функции у = sinx? если х = 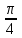 , х = , х =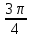 , , если х = 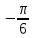 , х = , х =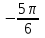 ? ?4. Изложение нового материала. Обобщение и конкретизация знаний, полученных ранее: 1)область определения, 2)множества значений, 3)четность или нечетность, 4) периодичность,5) точки пересечения с осями координат, 6) промежутки знакопостоянства, 7) промежутки возрастания и убывания, 8) наибольшее и наименьшее значение функции. Выделенные характеристики позволят построить сначала часть графика функции у = sinx на отрезке 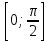 , затем на отрезке , затем на отрезке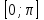 , потом на отрезке , потом на отрезке 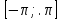 и , наконец на всей числовой прямой. и , наконец на всей числовой прямой.Так как значение синуса - ордината соответствующей точки единичной окружности. Поскольку ординату можно найти для любой точки единичной окружности, то область определения функции у = sinx - все действительные числа. Это можно записать так: D (sinx)= R. Для точек единичной окружности ординаты принимают все значения от -1 до 1, таким образом, для функции у = sinx область значений: у 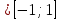 . Это можно записать так: Е(sinx) = . Это можно записать так: Е(sinx) = 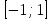 . .Синус – нечетная функция: sin(-x) = - sinx. Поэтому ее график симметричен относительно начала координат. Синус - периодическая функция с наименьшим положительным периодом Т = 2 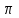 : sin(x+2 : sin(x+2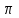 ) = sinx. Таким образом, через промежутки длиной 2 ) = sinx. Таким образом, через промежутки длиной 2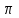 вид графика функции sinx повторяется. вид графика функции sinx повторяется.Чтобы найти точки пересечения графика функции с осями координат (на оси Оу значение х=0). Тогда соответствующее значение у =sin0=0, то есть график функции у = sinx проходит через начала координат. Функция обращается в нуль при х = 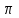 k, при k k, при k 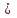 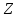 . .Как видим, наибольшее значение функции sinx равно единице. Это значение достигается только тогда, когда соответствующей точкой единичной окружности является точка, то есть при х = 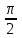 + 2 + 2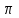 k, при k k, при k 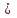 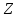 . .Наименьшее значение функции sinx равно минус единице. Это значение достигается только тогда, когда соответствующей точкой единичной окружности является точка, то есть при х = - 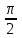 + 2 + 2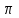 k, при k k, при k 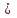 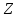 . А так же при х= . А так же при х=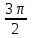 Для построения графика функции у = sinx на отрезке 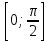 составим таблицу ее значений: составим таблицу ее значений:
Построим найденные точки и проведем через них кривую, учитывая, что на отрезке 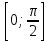 функция у = sinx возрастает. Получили график синуса на отрезке функция у = sinx возрастает. Получили график синуса на отрезке 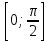 . Так как sin( . Так как sin(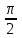 -x) = sin( -x) = sin(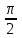 +x). То график синуса должен быть симметричен относительно прямой х = +x). То график синуса должен быть симметричен относительно прямой х =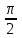 . Это позволяет построить график синуса на отрезке . Это позволяет построить график синуса на отрезке 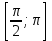 . Воспользовавшись нечетностью синуса. Получим график синуса на отрезке . Воспользовавшись нечетностью синуса. Получим график синуса на отрезке 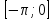 симметричным отображением построенной части синусоиды относительно начала координат. Так как на отрезке симметричным отображением построенной части синусоиды относительно начала координат. Так как на отрезке 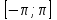 имеет длину, равную периоду синуса, то график синуса на всей числовой оси можно получить параллельным переносами построенной кривой. имеет длину, равную периоду синуса, то график синуса на всей числовой оси можно получить параллельным переносами построенной кривой.Затем учащиеся учатся изображать эскиз графика функции у = sin x по точкам и обобщают свойства функции. На этом этапе учащимся выдаются опорные конспекты (все свойства заносятся в таблицу). Построение графика функции на отрезке 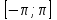 Значения синуса положительны (то есть ордината соответствующей точки единичной окружности положительна) в 1 и 11 четвертях. Таким образом, sin х>0 на отрезке (2πk; π+2πk), при k 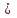 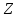 . . График функции у = sinx построен. График функции у = sinx построен. Промежутки знакопостоянства. Значения синуса положительны в 1 и 11 четвертях. Таким образом, sin x>0 на отрезке (2 πk ; π+2πk) k 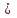 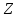 . .Промежутки знакопостоянства. Значения синуса отрицательны в 111 и 1V четвертях. Таким образом, sin x>0 на отрезке (π+2 πk ; 2π+2πk) k 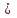 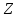 . .Если х 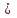 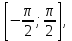 то при увеличении аргумента х ордината соответствующей точки единичной окружности увеличивается. Следовательно , на этом промежутке функция sin xвозрастает.Если х то при увеличении аргумента х ордината соответствующей точки единичной окружности увеличивается. Следовательно , на этом промежутке функция sin xвозрастает.Если х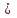  то при увеличении аргумента х ордината соответствующей точки единичной окружности уменьшается. Следовательно, на этом промежутке функция sin xубывает. то при увеличении аргумента х ордината соответствующей точки единичной окружности уменьшается. Следовательно, на этом промежутке функция sin xубывает.5. Закрепление первичных знаний. С помощью таблицы и графика функции у = sin x отвечают на теоретические вопросы Вместе с классом решаются задачи на сравнение; А) Сравнить числа sin 2 и sin 3 ; sin 1000 и sin 1300 ; sin 4и sin 2; Расположить в порядке возрастания числа sin 1.9; sin 3; sin(-1); sin(-1.5). Решение Числа sin 1.9 и sin 3 положительны, так как точки Р 1,9 и Р 3 находятся во 2 четверти. Функция у=sinх во 2 четверти убывает. sin 3 < sin 1.9 Числа sin(-1) и sin(-1.5) отрицательны, так как точка Р(-1) и Р(-1,5) находятся в 4 четверти. Функция у=sinх во 4 четверти возрастает.. sin(-1.5) < sin(-1.5) Ответ: Таким образом, в порядке возрастания эти числа располагаются так: sin(-1.5); sin(-1); sin 3; sin 1.9. 6. Зарядка для коррекции зрения. 7. Самостоятельное работа. Работа с таблицей. «Свойства функции у=соs x и ее график».  D(f)= E(f)= T= Четность: график симметричен относительно f возрастает при х 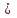 f убывает при х 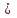 нули функции: х= f>0 при х 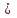 f<0 при х 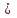 у наибольшее= при х= у наименьшее= при х= 8. Преобразование графиков тригонометрических функций. Сдвиг вдоль оси ординат. Задача на построение графиков функций у=sinх+3 и у=sinх-3 Обсуждение свойств функции. С 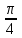 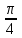 двиг вдоль оси абсцисс. двиг вдоль оси абсцисс.Задача на построение графиков функций у=sin(х - ) и у=соs(х+ ) Обсуждение свойств функции. Сжатие и растяжение к оси абсцисс Задача на построение графиков функций у= 3 sinх и у= 1/3 соsх Обсуждение свойств функции. С 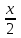 жатие и растяжение к оси ординат жатие и растяжение к оси ординатЗадача на построение графиков функций у = sin2х и у = соs Обсуждение свойств функции. 9, Историческая пауза об истории тригонометрии. Самой первой тригонометрической функцией была хорда, соответствующая данной дуге. Для этой функции были построены первые тригонометрические таблицы (II в. до н. э.), нужные для астрономии. Впервые в истории науки в период V-XII веков индийские математики и астрономы вместо полной хорды стали рассматривать половину хорды, которая соответствует современному понятию синуса. Величину половины хорды они назвали “архиджива”, что означало “половина тетивы лука”. Кроме sin x, индийцы рассматривали также величину 1 – cos x, которую они называли “комаджива”, и величину cos x – “котиджива”. Понятие таких тригонометрических функций, как тангенс, котангенс, секанс и косеканс, определил совершенно строго, исходя из рассмотрения тригонометрического круга, иранский математик Абу-ль-Вефа. Современные названия этих функций были даны в период с XV по XVII век европейскими учеными. Так, термин “тангенс” с латинского “касательная” был введен в XV веке основателем тригонометрии в Европе Региомонтаном. В XVI веке Финк вводит термин “секанс”. В XVII веке помощник изобретателя десятичных логарифмов Бриггса ученый Гюнтер вводит название “косинус” и “котангенс”, причем приставка “ко” (co) обозначает дополнение (complementum). Современные обозначения синуса и косинуса знаками sin x и cos x были впервые введены в 1739 году И. Бернулли в письме к петербургскому математику Л. Эйлеру. 10. Выполнение упражнений на преобразование графиков тригонометрических функций. Решить 6(1), 7(1). 11. Подведение итогов. Рефлексия. Д/з. Выставление оценок. Н 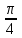 а уроке научились строить график функции у = sinx, у = соsx, читать свойства этого графика, строить эскиз графика, решать задачи связанные с использованием графика и свойств функции у = sinx, у = соsx. а уроке научились строить график функции у = sinx, у = соsx, читать свойства этого графика, строить эскиз графика, решать задачи связанные с использованием графика и свойств функции у = sinx, у = соsx.Построить график функции у = sin2х+3 и у = sin(х- ) Описать свойства функций у = sinx, у = соsx. Выучить п.19, решить №1(1), 2(1), 5(1,2). Тема урока: «Графики функций у=tg x и у=ctg x, их свойства» Цели урока: Ознакомить учащихся со свойствами функции у=tg x и у=ctg x, обучение построению графика функции у=tg x и у=ctg x, чтению этого графика, использование свойств и графика функции у=tg x и у=ctg x, при решении неравенств. Задачи урока. Образовательные – формировать умение построения графика функции у=tg x и у=ctg x, рассмотреть свойства графика, формировать навыки свободного чтения графиков, умение считывать свойства функции по графику. Развивающые – развивать логическое мышление, умение анализировать, обобщать полученные знания. Воспитательные – активизировать интерес к получению новых знаний, воспитывать графическую культуру, формировать точность и аккуратность при выполнении чертежей. Ход урока 1. Организационный момент. Приветствие. Эмоциональный настрой на урок. 2. Объявление темы и цели урока. Тема урока: «Свойства функций у=tg x и у=ctg x и их графики». Сегодня рассмотрим свойства функции у=tg x и у=ctg x и построим графики. Рассмотрим простейшие преобразования функции, построим графики этих функций и перечислим их свойства. Из истории. Тригонометрия – слово греческое и в буквальном переводе означает измерение треугольников. В данном случае измерение треугольников следует понимать как решение треугольников, т.е. определение сторон, углов и других элементов треугольника, если даны некоторые из них. Большое количество практических задач, а также задач планиметрии, стереометрии, астрономии и других приводятся к задаче решения треугольников. Возникновение тригонометрии связано с землемерением, астрономией и строительным делом. Хотя название науки возникло сравнительно недавно, многие относимые сейчас к тригонометрии понятия и факты были известны ещё две тысячи лет назад. Понятие таких тригонометрических функций, как тангенс, котангенс, определил совершенно строго, исходя из рассмотрения тригонометрического круга, иранский математик Абу-ль-Вефа. Современные названия этих функций были даны в период с XV по XVII век европейскими учеными. Так, термин “тангенс” с латинского “касательная” был введен в XV веке основателем тригонометрии в Европе Региомонтаном. 3 Актуализация опорных знаний: Выполнение устных упражнений. Повторить определение тригонометрических функций и знаки значений этих функций. Затем учащиеся отвечают на вопросы: Учащимся предложена иллюстрация единичной окружности. Тригонометрия на руке. Работа с таблицей с. Какой знак имеет значение функции у = tg x? если х = 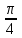 , х = , х =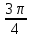 , , если х = 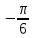 , х = , х =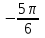 ? ?Самостоятельная работа Вариант 1 №1. Вычислите: 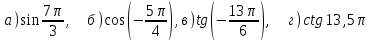 . .№2. Найдите заданную точку на числовой окружности: 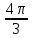 , , 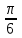 ; -3,5; 240˚,180˚ ; -3,5; 240˚,180˚№3. Вычислите 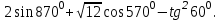 Вариант 2 №1. Вычислите: 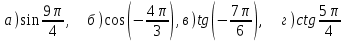 №2. Найдите заданную точку на числовой окружности: 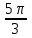 , , 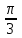 ; -1,5; 340˚,270˚ ; -1,5; 340˚,270˚№3.Вычислите: 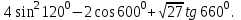 4. Изложение нового материала. Что кружится, что ложится И на землю, и на крыши, И о чем поэт зимою По ночам поэмы пишет? Это первое словечко А второе просто «на». Ну, а третье? Угадайте, Что бежит по проводам? Напиши, что получилось, И прочти наоборот. Не запутайся, читая Слово задом наперед! (Снег-на-ток…котангенс) Обобщение и конкретизация знаний, полученных ранее: 1)область определения, 2)множества значений, 3)четность или нечетность, 4) периодичность,5) точки пересечения с осями координат, 6) промежутки знакопостоянства, 7) промежутки возрастания и убывания, 8) наибольшее и наименьшее значение функции. Выделенные характеристики позволят построить сначала часть графика функции у=tg x 1) Область определения функции – множество всех действительных чисел, кроме чисел вида x = π/2 + πk, где k – любое целое число. Это означает, что на графике функции нет точки, принадлежащей прямой x = π/2, либо прямой x = 3π/2, либо прямой x = 5π/2, либо прямой x = –π/2 и т.д. 2) Область значений функции (–∞; +∞) 3) Это нечетная функция. 4) Это непрерывная функция на интервале (–π/2; π/2). 5) Это периодическая функция с основным периодом π (Т = π) 6) Функция возрастает на интервале (–π/2; π/2). 7) Функция не ограничена ни сверху, ни снизу. Не имеет ни наименьшего, ни наибольшего значений. Просмотр презентации. Работа с учебником: Свойства и график функции у=ctg x. 1) Область определения функции – множество всех действительных чисел, кроме чисел вида x = πk, где k – любое целое число. 2) Область значений функции (–∞; +∞) 3) Это нечетная функция. 4) Это непрерывная функция. 5) Это периодическая функция с основным периодом π (Т = π) 6) Функция убывает в промежутке (πk; π + πk), где k – любое целое число. 7) Функция не ограничена ни сверху, ни снизу. Не имеет ни наименьшего, ни наибольшего значений. 5. Закрепление первичных знаний. Решение упражнений на сравнение, преобразование графиков функцй: №3, 4, 7. 8. 6. Зарядка для коррекции зрения. 7. Самостоятельное работа. 8. Подготовка к ВНО. 11. Подведение итогов. Рефлексия. Д/з. Выставление оценок. На уроке научились строить график функции у=tg x и у=ctg x, читать свойства этого графика, строить эскиз графика, решать задания, связанные с использованием графика и свойств функций. Выучить п.19, решить № 3(1), 4(1), 7(1,2). Урок обобщения и систематизации знаний по теме «Свойства тригонометрических функций». Цель: - организовать деятельность учащихся по формированию знаний свойств тригонометрических функций, умений применять свойства и простейшие преобразования для построения графиков тригонометрических функций. - содействовать развитию исследовательских навыков; умений аргументировать, классифицировать. - содействовать развитию инициативности, трудолюбия, развития письменной и графической культуры.. Ход урока 1. Организационный момент. Приветствие. Эмоциональный настрой на урок. 2. Объявление темы и цели урока. Сегодня у нас обобщающий урок по теме: «Свойства тригонометрических функций». На уроке вы должны показать свои знания теории по данной теме, т. е. знание определений, формул, а также умение применять эти знания при решении задач. Урок пройдет в несколько этапов. За каждый этап будут даваться определенное количество баллов: индивидуально или команде. На доске представлена система оценок за урок и таблица для подсчета баллов командам:
Всего будет три команды в соответствии с рядом. Один ряд – команда синусов. Второй ряд – команда косинусов. Третий ряд – команда тангенсов. Прежде чем приступить к первому этапу, отметьте свое настроение в начале урока (поставьте знак «+» в том столбце, где нарисована мордочка, соответствующая вашему настроению). Вторую строчку таблицы вы заполните в конце урока. 3 Актуализация опорных знаний: Разминка «Дальше- дальше»…. 1. Дайте определение синуса любого угла. 2. В каких четвертях синус положительный. 3. Каким должен быть острый угол, чтоб синус и косинус его были равны? 4. Дайте определение тангенса и котангенса. 5. В каких четвертях синус и котангенс имеют одинаковые знаки. 6. Чем отличается друг от друга область определения функций синуса и тангенса? 7. Какие тригонометрические функции являются четными, нечетными? 8. Назовите основные периоды тригонометрических функций. 9. Какова область значений синуса, косинуса? 10. Почему в прямоугольном треугольнике синус и косинус любого угла всегда меньше единицы? «Табличный» вопрос. Три ученика назначаются помощниками учителя. Каждый ученик получает задания на карточках. Необходимо заполнить таблицу значений для своей тригонометрической функции для углов: 0,30, 45,60, 90,180,270,360 градусов. За все верные ответы – 1 балл, за все верные, кроме одной - 0,5 балла.
Помощники собирают листочки и проверяют выполнение заданий. Затем отмечают баллы в таблице. На доске нарисована таблица для подсчета баллов по каждой команде. 4. Обобщение и систематизация знаний по теме «Свойства тригонометрических функций» Рисуем, вычисляем. №1. Найдите заданную точку на числовой окружности: 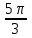 , , 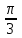 ; -1,5; 340˚,270˚ ; -1,5; 340˚,270˚№2. Вычислите: 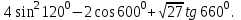 Работа в команде. Затем –самопроверка.. Историческая справка. Слово «тригонометрия» произошло от греческого. Тригонон означает треугольник, метрео – измерение, т.е. тригонометрия – измерение треугольников. Возникновение тригонометрии связано с потребностями человека в астрономических знаниях. В древности люди наблюдали за движением светил, чтобы по данным наблюдениям вести календарь и правильно предугадать направление движения корабля в море или каравана в пустыне. Так как расстояние от Земли до звезд и планет непосредственно измерить нельзя, то пришлось искать взаимосвязи между сторонами и углами треугольников, две вершины которых расположены на Земле, а третья представляется точкой на звездном небе. Так возникла тригонометрия. Решение упражнений на сравнение, преобразование графиков функций: №3, 4, 7, 8. Определить наименьший положительный период функций: 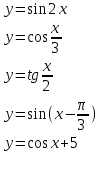 Определить, является функция чётной или нечётной 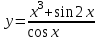 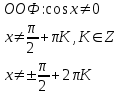 ООФ симметрична относительно начала координат. 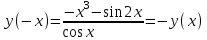 функция нечётная. функция нечётная.А теперь, ребята, повторим свойства известных нам тригонометрических функций. Назовите мне свойства этой функции Y = sin X (рис. 1). 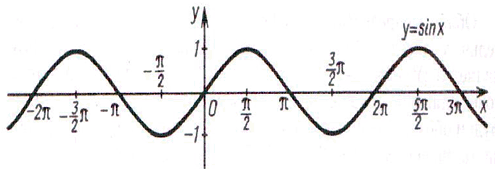 Свойства: D(sin)=R E(sin)=[-1;1] sin(-x)=-sin, функция нечётная Наименьший положительный период: 2π Sin (x+2πn)= sin x, n Є Z, x Є R. sin x=0 при x=πk, kЄ Z sin x>0, x Є (2πk;π+2πk), k Є Z sin x<0, x Є(π+2πk; 2π+2πk), k Є Z Наибольшее значение, равное 1, y=sin x принимает в точках x=π/2+ 2πk, k Є Z. Наименьшее значение, равное -1 y=sin x принимает в точках x=3π/2+ 2πk, k Є Z. Обратите внимание на следующий график y= cos x (рис. 2.) 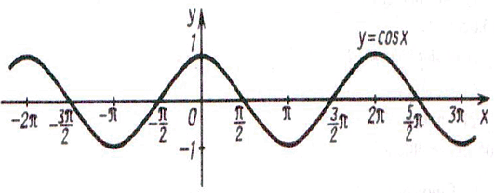 Свойства: D (cos)=R E (cos)=[-1;1] cos(-x)= cos x, функция чётная Наименьший положительный период: 2π Cos (x+2πn)=cos x, n Є Z, x Є R cos x=0 при x=π/2+πk, kЄZ cos x>0, x Є (-π/2+2πk; π/2+2πk), k Є Z cos x<0, x Є (π/2+2πk; 3π/2+2πk), k Є Z Наибольшее значение, равное 1, y=cos x принимает в точках x= 2πk, k Є Z. Наименьшее значение, равное -1 y=cos x принимает в точках x=π+ 2πk, k Є Z. 5. Зарядка для коррекции зрения. Методика Базарного. 6. Подготовка к ВНО. Повторение «Функции». Решение упражнений. 7. Самостоятельное работа. Найдите градусную меру угла, радианная мера которого равна: 1)0,5 2)10 3)π/5 4)π/9 5)3/4π 6)-5/6π 7)-9/12π 8)12π Найдите радианную меру угла, равного: 1)1350 2)2100 3)360 4)1500 5)2400 6)3000 7) -1200 8)-225ĕ Определите знак выражения: 1) sin5π/6 2) cos3π/4 3)sin 1 4)cos 0,9 5)tg π/4 6)tg 3 Найдите значение выражения: 1) 2sin π -2cos 3π/2 +3tg π/4 –ctg π/2 2) sin (- π/4) +3 cos π/3 – tg π/6 + tg π 3) 2sin π/4 -3 tg π/6 +ctg (-3π/2) -tg π 4) 3 tg(-π/4)+2sin π/4 -3tg0- 2ctg π/4 Начинаем? Дамы и господа! Леди и джентльмены! Сегодня у нас аукцион. С молотка пойдет имение графини Функции “Высокие горы, глубокие каньоны”. Покупка акций требует от вас профессионального мастерства и глубоких математических и информационных познаний, находчивости, остроумия. Наша графиня – большая оригиналка. У каждой акции своя “изюминка”. Для всех присутствующих небольшая справка – условия, при которых вы можете принять участие в аукционе : Надо отгадать, что продается. Тот, кто отгадает, получает акцию синего цвета. Надо назвать свою цену, то есть найти ответ. Решивший назвать цену (давший правильный ответ), получает одну акцию красного цвета, причем одна акция красного цвета равна трем акциям синего цвета. На обдумывание цены отводится определенное время (1–5 мин). Набравший наибольшее количество акций становится председателем акционерного общества. На доске весит карта Донецкой области. 1. Продается географическая карта. Что продается? Один из учеников дает ответ. Если произнесен неправильный ответ, то учитель говорит: “Кто больше?” услышав верный ответ, произносит: “Продано”, и отвечающему дается красная или синяя акции. Если не прозвучит правильный ответ, то акция остается у графини. – Верно, продается область определения. (Отгадавший получает акцию синего цвета.) Визитная карточка этого поместья: Вариант 1. Вариант 2. 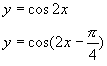 Вы должны назвать цену (1 минута на обдумывание) этой акции, то есть найти область определения данной функции. 2. Наша уважаемая графиня очень любит музыку, и одно из своих любимых произведений она решила представить вам. (звучит музыка Моцарта, где ясно прослушиваться периоды.) Дамы и господа! Ваши ответы. Ответ. Периодичность (акция синего цвета). Кто станет обладателем акции красного цвета? Время на обдумывание 1-2 минута. 3. Графиня также обожает живопись и она представляет вам одну из картин своей коллекции. Ответ. Четность (акция синего цвета).  Кто станет обладателем красной акции? Время на обдумывание 3 минуты. 4. Следующая акция зашифрована в этой картине. Кто получает акции синего цвета? Ответ. Точки пересечения с осями координат.  Теперь ваша задача решиться на какую-то цену и стать обладателем двух красных акций. 5. Вот еще одна картина из коллекции графини. На ней изображен ребус. Разгадайте его и вы получите акцию синего цвета. Ответ. Производная.  Дамы и господа! Прошу назвать ваши цены! Торопитесь! Время на обдумывание 2 минуты. 6. И вновь картина из коллекции графини. Ответ. Точки экстремума.  Продано. Вы получаете акцию синего цвета. Кто же станет обладателем трех акций красного цвета? Найдите интервалы монотонности, наибольшее и наименьшее значение функции. Время на обдумывание 5–7 минут. Чтобы расшифровать следующую акцию, нужно определить какое из свойств тригонометрических функций описано в каждой из этих пословиц? Пословицы и поговорки Декабрь год кончает, а зиму начинает. У дороги конца нет. Повторенье - мать ученья. Не поклонясь до земли, и грибка не поднять. Оглядывайся на себя по три раза в день. Продано! Вы получаете акцию синего цвета. Я говорю: Конь – лошадь – жеребенок; Кот – кошка – котенок; Бык – корова – теленок; Баран – овца – ягненок; Король – королева – принц; Граф – графиня – … Ответ. График. Изобразите в виде графиков тригонометрических функций смысл поговорки: 1) "Выше меры конь не скачет" у=|cos x| или y=|sin x| 2) Чем дальше в лес, тем больше дров 3) Тише едешь, дальше будешь Сообщение: Графики тригонометрических функций нашли применение во многих отраслях. Например, в области изобразительного искусства. Как-то раз итальянский геометр Гвидо Гранди (1671-1742) создал розы. Нет, вовсе не те прекрасные растения, которые известны всем. Розы Гвидо Гранди радуют глаз правильными и плавными линиями, но их очертание не каприз природы – они предопределены математическими зависимостями. Семейство роз Гвидо Гранди описывается графиком функции у = а*sin k , где а и k - некоторые числа. На рисунке изображены эти кривые при различных параметрах k. Очарованный результатами Гранди, немецкий геометр XIX в. Хабенихт также решил заняться математическим: «растениеводством». Хабенихт, путем многочисленных экспериментов «вырастил» замечательные экспонаты. А свои прекрасные цветы Гвидо Гранди собрал в одну книгу и назвал её «Цветник роз». В наши дни подобные эксперименты удобно проводить, имея под рукой персональный компьютер. Тригонометрические функции также нашли применение в области физики. Давайте послушаем сообщение, приготовленное учащимся вашего класса. Графики можно складывать. На примере вы видите суммирующий зеленый график двух функций с одинаковым периодом. 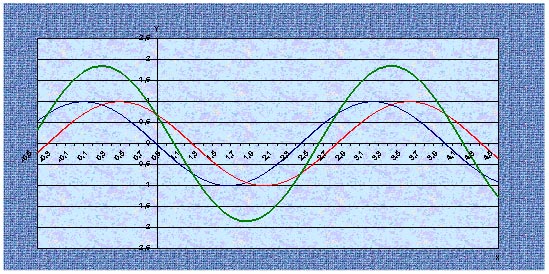 Сложение графиков можно наблюдать в природе. В физике это явление называется интерференцией. Процедура сложения гармонических колебаний – не формальный математический прием. Она тесно связана с реальными физическими процессами, самыми распространенными из которых является звук и свет. Своеобразие, прелесть и красота звуков различных голосов и музыкальных инструментов получается при сложении простых или “чистых” тонов, частоты колебаний которых относятся как 1 : 2 : 3 : 4 и т.д. Наиболее низкий звук называется основным, а все остальные, более высокие тона называются высшими тонами или обертонами. “Чистый” тон графически изображается синусоидой, как и положено гармоническим колебаниям, а звук, например, трубы дает тоже периодический, но сложный по форме график, получаемый сложением различных тонов. Сложение волн в пространстве называется интерференцией. Если звуки одинаковых частот наложить друг на друга, то амплитуда суммарных колебаний может как удвоиться, так и стать равной нулю. Все зависит от того складываются ли волны без разности фаз или в противофазе. Не надо обладать музыкальным слухом, чтобы заметить, как изменится тон, высота звука, гудка локомотива, когда встречный поезд проносится мимо вас. Пока оба поезда сближаются, тон был намного выше, чем после встречи, когда поезда начали удаляться друг от друга. Отчего же это происходит? Гудок встречного локомотива издает все время один и тот же звук вполне определенной частоты. Но ухо воспринимает различное число колебаний в секунду, в зависимости от того, двигаетесь ли вы навстречу гудку или удаляетесь от него. Двигаясь навстречу, человек за секунду улавливаете больше колебаний, так как источник звука сам движется навстречу. Звук кажется выше. И все происходит наоборот, если вы удаляетесь от источника – тогда звук кажется ниже по тону. Такой эффект кажущегося изменения частоты называется эффектом Доплера, по имени австрийского физика Кристиана Доплера (1803–1853). Изменение частоты у световых волн приводит к изменению цвета - чем выше частота, тем ближе к фиолетовому и дальше от красного будет цвет. Стало быть, при движении навстречу источнику света, красный цвет изменится на желтый, а, возможно, на зеленый, синий и фиолетовый. Анекдотичный случай произошел с американским физиком-экспериментатором Робертом Вудом (1868–1955). Однажды полицейский остановил автомобиль Вуда за езду на красный цвет. Вуд, пытаясь оправдаться, рассказал полицейскому, что при движении навстречу источнику красного цвета из-за эффекта Доплера этот цвет вполне мог показаться ему зеленым. Но полицейский все-таки оштрафовал Вуда, не за езду на красный свет, а за превышение скорости. Еще бы – для того, чтобы принять красный свет за зеленый, Вуд должен был мчаться навстречу светофору с фантастической скоростью в 135 млн км/ч. Но шутка – шуткой, а именно эффект Доплера позволил ученым сделать вывод о расширении Вселенной, и о том, что когда-то она была “сжата в точку”. Функция. Прочтите наоборот. 1)Что кружится, что ложится И на землю, и на крыши И о чем поэт зимою По ночам поэмы пишет? Это первое словечко. 2) А второе просто "на" 3) Ну, а третье? Угадайте, Что бежит по проводам? Напиши, что получилось И прочти наоборот Не запутайся, читая, Слово задом наперед. (снег на ток - котангенс) 1)Привычное слово кудлатой наседки Поставьте на первое место: 2) На месте втором посмотрите-ка - нота. Важна для любого оркестра 3) На третьем одна одинокая буква, пятнадцатая в алфавите 4) Один из волос на мордашке котенка На месте четвертом прочтите. Ответ: косинус. Рожденный пустыней колеблется звук. Колеблется синий на нитке паук. Колеблется воздух, прозрачен и чист. В сияющих звездах колеблется, лист. Теперь выясним, кто станет председателем акционерного общества. Напоминаю: одна акция красного цвета равна трем акциям синего. Идет подсчет количества акций и затем объявляется результат. – Поздравляем председателя. Аукцион окончен. Имение графини продано! 8. Рефлексия (цветовая) Постройте график функции у=2cosx одним из следующих цветов, которые на ваш взгляд соответствуют вашему настроению от проделанной вами работы Красный - отличное Зеленый - хорошее Синий – удовлетворительное О какой кривой идёт речь? Как утомительны вечные спуски, Как утомительны вечные взлёты!... В каждой ложбинке, На каждой вершине – Тщетна надежда – мечта о привале, Об остановке и передышке. (синусоида) 9. Подведение итогов. Д/з. Выставление оценок. Повторить п.17-19, решить № 3(3), 4(3), 7(3), 8(4). Презентация «Из истории тригонометрии». Тема: Контрольная работа по теме «Свойства тригонометрических функций» Цель: Проверить уровень усвоения данной темы и уровень умений и навыков, сформированный по данной теме. Развитие самоконтроля и самопроверки. Воспитание трудолюбия и ответственности за выполнение работы. Ход урока. 1.Организационный этап. 2.Постановка темы и цели урока. 3.Условие контрольной работы. 4.Итоги урока. Домашнее задание. 1 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||