Лекция 3. Основы математической логики. Лекция 3 Основы математической логики Основные понятия математической логики
 Скачать 55.71 Kb. Скачать 55.71 Kb.
|
|
Лекция №3 Основы математической логики 1. Основные понятия математической логики Математическая логика – это раздел математики, изучающий математические обозначения, формальные системы, доказуемость математических суждений, природу математического доказательства в целом и другие аспекты оснований математики; это логика, развиваемая математическими методами. Основным понятием математической логики является понятие высказывания. Определение. Высказывание – это утверждение, относительно которого можно сказать истинно оно или ложно. Высказывания обозначаются заглавными буквами латинского алфавита: А, В, … . Пример. А – «Ока – приток Волги» – истинное высказывание; В – «2 + 2 = 5» – ложное высказывание; « x > 6» не является высказыванием. Вопросительное и побудительное предложения не являются высказываниями. Любое высказывание бывает либо истинным, либо ложным; быть одновременно и тем, и другим оно не может. 2. Логические операции над высказываниями Определение. Высказывание называется простым, если никакая его часть сама не является высказыванием; в противном случае высказывание называется сложным. Сложные высказывания образуются из простых при помощи союзов «и», «или», «если,… то», «тогда и только тогда» и т. д. В математической логике эти союзы называются логическими связками. Истинность сложного высказывания зависит от того, истинны или ложны входящие в него простые высказывания. Изучение этой зависимости является предметом логики высказываний. Определение. Отрицание высказывания А – это высказывание А (или ¬А) (читается «не А», «неверно, что А»), которое истинно, когда исходное высказывание А ложно, и ложно, когда А истинно. Пример. С – «Маша любит кашу», С – «Неверно, что Маша любит кашу». Определение. Конъюнкция высказываний А и В (логическое умножение) – это высказывание А∧ В (читается «А и В»), которое истинно, когда оба высказывания истинны, и ложно во всех остальных случаях. Пример. Для высказываний А и В (см. пример п. 1) конъюнкцией является предложение А∧ В – «Ока – приток Волги и 2 + 2 = 5», которое ложно. Определение. Дизъюнкция высказываний А и В (логическая сумма) – это высказывание А∨ В (читается «А или В»), которое ложно, когда ложны оба высказывания А и В, и истинно в остальных случаях. Пример. Для высказываний А и В (см. пример п. 1) дизъюнкцией является предложение А∨ В – «Ока – приток Волги или 2 + 2 = 5», которое истинно. Определение. Импликация высказываний А и В – это высказывание А→В (читается «из А следует В», либо «если А, то В»), которое ложно, когда А – истинно, В – ложно, и истинно во всех остальных случаях. Пример. Для высказываний А и В (см. пример п. 1) импликацией является предложение А→В – «если Ока – приток Волги, то 2 + 2 = 5», которое ложно. Определение. Эквиваленция высказываний А и В – это высказывание А↔В (читается «А эквивалентно В», «А тогда и только тогда, когда В», «А необходимо и достаточно для В», «А равносильно В»), которое истинно, когда оба высказывания истинны или оба ложны, и ложно в остальных случаях. Пример. Для высказываний А и В (см. пример п. 1) эквиваленцией является предложение А↔В – «Ока – приток Волги тогда и только тогда, когда 2 + 2 = 5», которое ложно. Результаты всех логических операций можно представить в виде следующей таблицы истинности (логические значения: истина=1, ложь=0):
3. Формулы алгебры высказываний Алгебра высказываний – это раздел математической логики, в котором изучаются логические операции над высказываниями. Логическая формула – запись сложного высказывания в виде простых высказываний, соединенных операциями отрицания, конъюнкции, дизъюнкции, импликации, эквиваленции и скобок. В случае, если в логической формуле присутствуют несколько операций, не разделенных скобками, то порядок выполнения операций следующий: отрицание; конъюнкция; дизъюнкция; импликация; эквиваленция; Рассмотрим сложное высказывание ((А∧ В) ∨ A)↔B , где А и В – простые высказывания (см. пример п. 1). Пусть вместо конкретных высказываний А и В взяты переменные, которые назовём пропозиционными, тогда получим формулу алгебры высказываний ((X ∧Y ) ∨ X )↔Y , где X, Y – некоторые произвольные высказывания. Используя пропозиционные переменные X, Y, Z, … , конкретные высказывания А, В, С, … , а также знаки логических операций (¬, ∧, ∨,→,↔) и логические константы («1», «0»), можно записать формулы алгебры высказываний. Если вместо пропозиционных переменных подставить конкретные высказывания, то формула превратится в некоторое сложное высказывание. Для каждой формулы можно составить таблицу истинности. При их составлении необходимо учитывать порядок выполняемых действий. Если в формуле нет скобок, то логические операции выполняются в следующем порядке: отрицание, конъюнкция, дизъюнкция, импликация, эквиваленция. Пример. Составить таблицу истинности для формулы (А∨ В) ∧ ( 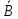 → А)↔ → А)↔ 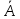 ≡ (*) . ( ≡ (*) . (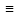 - равно при любых значениях переменной) - равно при любых значениях переменной)Решение.
Определение. Формула называется тождественно истинной или тавтологией, если она обращается в истинное высказывание при всех наборах значений переменных. Определение. Формула называется тождественно ложной или противоречием, если она обращается в ложное высказывание при всех наборах значений переменных. Пример. А∧ 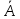 – противоречие, А∨ – противоречие, А∨ 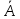 – тавтология. – тавтология.4. Законы алгебры высказываний Определение. Две формулы называются равносильными (тождественными), если они принимают одинаковые логические значения при одинаковых наборах значений входящих в них выражений. Равносильные формулы обозначаются знаком " ≡ ". Часто применяющиеся основные равносильности называются законами алгебры высказываний: 1. 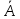 ≡ А – закон двойного отрицания. ≡ А – закон двойного отрицания.2. А∧ 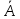 ≡ 0 – закон противоречия. ≡ 0 – закон противоречия.3. А∨ 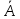 ≡1 – закон исключенного третьего. ≡1 – закон исключенного третьего.4. А∧1 ≡ А, А∧ 0 ≡ 0 , А∨1 ≡ 1, А∨ 0 ≡ А – законы сочленения переменной с константой. 5. А∧ А ≡ А, А∨ А ≡ А – закон идемпотентности. 6. А∧ В ≡ В ∧ А, А∨ В ≡ В ∨ А – закон коммутативности. 7. (А∧ В) ∧ С ≡ А∧ (В ∧С), (А∨ В) ∨С ≡ А∨ (В ∨С)– законы ассоциативности. 8. А∧ (В ∨ С) ≡ (А∧ В) ∨ (А ∧ С) ,А∨ (В ∧ С) ≡ (А∨ В) ∧ (А∨ С) – законы дистрибутивности. 9. 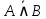 ≡ ≡ 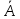 ∨ ∨ 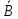 , , 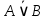 ≡ ≡ 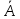 ∧ ∧ 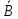 – законы де Моргана. – законы де Моргана.10. А ∧ (А∨ В) ≡ А, А∨ (А ∧ В) ≡ А – законы поглощения. 11. (А∨ В) ∧ ( 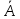 ∨ В) ≡ В, (А ∧ В) ∨ ( ∨ В) ≡ В, (А ∧ В) ∨ (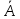 ∧ В) ≡ В – законы склеивания. ∧ В) ≡ В – законы склеивания.12. А↔ А ≡ 1, А→ А ≡ 1 – законы тождества. 13. А→ В ≡ 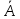 ∨ В – закон замены импликации на дизъюнкцию. ∨ В – закон замены импликации на дизъюнкцию.14. А↔В ≡ (А→ В) ∧ (В→ А) – закон замены эквиваленции на импликации. 15. А→В ≡ 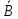 → → 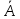 – закон контрапозиции. – закон контрапозиции.Доказать эти законы можно при помощи таблиц истинности. Пример. Докажем закон № 6 алгебры высказываний А∧ В ≡ В ∧ А, составив таблицу истинности. Доказательство.
В столбцах, соответствующих левой и правой частям данного закона, получены одинаковые логические значения, следовательно, закон доказан. Используя основные равносильности, можно от одной формулы переходить к равносильной ей формуле. Такой переход называется равносильным преобразованием исходной формулы. Равносильные преобразования формул применяются, прежде всего, для упрощения формул. 5. Предикаты и кванторы Предикат – это предложение с переменными, которое после замены переменных определенными их значениями превращается в высказывание. Если предикат содержит одну переменную х, то его обозначают 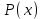 , если предикат содержит две переменные х и у, то его обозначают , если предикат содержит две переменные х и у, то его обозначают 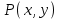 и т.д. и т.д.Например: а) 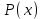 : «х – четное число» является предикатом; : «х – четное число» является предикатом;б) любое уравнение или неравенство является предикатом. Для предикатов аналогично определены те же операции, что и для высказываний. Например: а) система уравнений или неравенств – конъюнкция предикатов; б) совокупность уравнений или неравенств – дизъюнкция предикатов. Существуют 2 вида кванторов: Квантор всеобщности. Обозначается 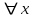 . Запись . Запись 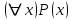 читается как «Для любого х выполняется Р(х)» или «Для всех х верно Р(х)» или «Для каждого х Р(х)». читается как «Для любого х выполняется Р(х)» или «Для всех х верно Р(х)» или «Для каждого х Р(х)».Квантор существования. Обозначается 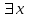 . Запись . Запись 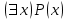 «Существует х, такое что «Существует х, такое что 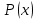 » или «Для некоторых х верно » или «Для некоторых х верно 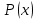 » или «Хотя бы один х » или «Хотя бы один х 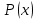 ». ».Например: Пусть 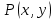 : «Официант х обслуживает стол у». Тогда : «Официант х обслуживает стол у». Тогда 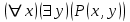 означает«У любого официанта есть стол, который он обслуживает». означает«У любого официанта есть стол, который он обслуживает».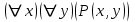 означает«Каждый официант обслуживает все столы». означает«Каждый официант обслуживает все столы».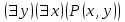 означает«Существует стол, который обслуживается некоторым официантом». означает«Существует стол, который обслуживается некоторым официантом».Для любого предиката 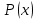 имеют место следующие равносильности: имеют место следующие равносильности: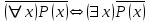 ; ;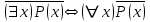 . .Эти правила используются для построения отрицаний предложений. Например: Постройте отрицание предложения «Некоторые студенты нашего факультета не сдали сессию». Решение: Р(х): «Студент х нашего факультета не сдал сессию». Тогда исходное предложение запишется как 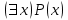 , а его отрицание как , а его отрицание как 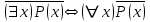 , что читается как «Все студенты нашего факультета сдали сессию». , что читается как «Все студенты нашего факультета сдали сессию».5. Приложение алгебры высказываний к логикоматематической практике Многие математические теоремы имеют структуру, выражаемую формулой X →Y , где утверждение Х называется условием теоремы, Y – заключением. Примем её за прямую теорему. Из неё можно получить новые теоремы: Y → X – обратная теорема, 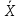 → →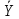 – противоположная теорема, – противоположная теорема,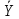 → → 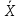 – обратная противоположной теореме. – обратная противоположной теореме.Из закона № 15 логики высказываний следует, что если верна прямая теорема, то верна и обратная противоположной теорема и наоборот. Аналогично, если верна обратная теорема, то верна и противоположная теорема и наоборот. Например. Определение. Для теоремы X →Y высказывание Y называется необходимым условием для высказывания Х, а высказывание Х называется достаточным условием для Y. Пример. Прямая теорема. Если четырехугольник - ромб, то его диагонали пересекаются под прямым углом.(истина) Обратная теорема. Если диагонали четырехугольника пересекаются под прямым углом, то этот четырехугольник – ромб.(ложь) Противоположная теорема. Если четырехугольник- не ромб, то его диагонали пересекаются под прямым углом. (ложь) Обратная противоположной. Если диагонали пересекаются не под прямым углом, то четырехугольник- не ромб.(истина) Контрольные вопросы 1. Что является предметом математической логики? 2. Дайте определение высказывания. 3. Дайте определение отрицания, конъюнкции, дизъюнкции, импликации и эквиваленции высказываний. 4. Что является предметом алгебры высказываний? 5. Как образуются формулы алгебры высказываний? 6. Какая формула называется тавтологией (противоречием)? 7. Дайте определение равносильных формул. 8. Сформулируйте законы алгебры высказываний. 10. Какие четыре вида теорем существуют? |
