Погрешности измерений. Лекция 3 Погрешности измерений. Лекция 3 погрешности измерений 1 Постулаты метрологии. Классификация погрешностей
 Скачать 129.5 Kb.
|
|
Лекция 3 ПОГРЕШНОСТИ ИЗМЕРЕНИЙ 3.1 Постулаты метрологии. Классификация погрешностей Качество средств и результатов измерений принято характеризовать, указывая их погрешности. Введение понятия "погрешность" требует определения и четкого разграничения трех понятий: истинного и действительного значений измеряемой физической величины и результата измерения. Истинное значение хи физической величины – это значение, идеальным образом отражающее свойство данного объекта как в количественном, так и в качественном отношении. Оно не зависит от средств нашего познания и является той абсолютной истиной, к которой мы стремимся, пытаясь выразить ее в виде числовых значений. На практике истинное значение практически всегда неизвестно (в редких случаях оно может быть определено с применением первичных или вторичных эталонов), поэтому его приходится заменять понятием "действительное значение". Действительное значение хд физической величины– значение, найденное экспериментально и настолько приближающееся к истинному, что для данной цели оно может быть использовано вместо него. Действительное значение может быть получено при помощи рабочих эталонов. Результат измерения (измеренное значение) хпредставляет собой приближенную оценку истинного значения величины, найденную путем измерения (результат, полученный с помощью рабочего средства измерения). Изложенное позволяет сформулировать два постулата метрологии: Истинное значение определяемой величины существует, и оно постоянно. Истинное значение измеряемой величины отыскать невозможно. Отсюда следует, что результат измерения х, как правило, математически связан с измеряемой величиной вероятностной зависимостью. При практическом использовании тех или иных измерений важно оценить их точность. Термин "точность измерений", т. е. степень приближения результатов измерения к некоторому действительному значению, не имеет строгого определения и используется для качественного сравнения измерительных операций. Для количественной оценки используется понятие "погрешность" (чем меньше погрешность, тем выше точность). Понятие "погрешность" – одно из центральных в метрологии, а оценка погрешности измерений — одно из важных мероприятий по обеспечению единства измерений. В метрологии используются понятия "погрешность результата измерения" и "погрешность средства измерения". Погрешность измерения Δxизм – это отклонение результата измерения х от истинного (действительного) хи (хд) значения измеряемой величины: Δxизм = х – хи, или Δxизм = х – хд. Погрешность средства измерения - отклонение показания средства измерения от истинного (действительного) значения измеряемой величины. Оно характеризует точность результатов измерений, проводимых данным средством. Эти два понятия во многом близки друг к другу и классифицируются по одинаковым признакам. Погрешность измерения включает в себя множество различных составляющих, которые можно классифицировать по различным признакам. В настоящее время классификация погрешностей содержит около 30 видов (см. пример классификации на рис 3.1). Погрешности измерения можно разделить: по характеру (закономерностям) проявления или изменения от измерения к измерению – на случайные, систематические и грубые промахи, по формам числового выражения – абсолютные, относительные и приведенные; по источникам возникновения – на методические, инструментальные, субъективные (погрешности оператора), которые, в свою очередь, могут быть как случайными, так и систематическими; по характеру изменения во времени – на статические и динамические; по характеру принадлежности (близости) результатов наблюдений к основной совокупности выделяют грубые погрешности и промахи. по уровню имеющейся информации – определенные и неопределенные; по формам используемых оценок - среднее квадратическое значение, доверительные границы погрешности и др.; по возможности выявления и исключения из результатов измерения – на выявленные и невыявленные, устранимые и неустранимые, исключенные и неисключенные;  Рисунок 3.1 – Классификация погрешностей измерения. 3.2 Систематические погрешности Систематическая погрешность – это составляющая погрешности измерения, которая остаётся постоянной или закономерно изменяется при повторных измерениях. К систематическим погрешностям измерений можно отнести те составляющие, для которых можно считать доказанным наличие функциональных связей с вызывающими их аргументами. Для них можно предложить следующее определение: систематическая погрешность – закономерно изменяющаяся составляющая погрешности измерений. Формально это записывается в виде  , где  – аргументы, вызывающие систематическую погрешность. Главной особенностью систематической погрешности являетсяпринципиальная возможность ее выявления, прогнозирования и однозначной оценки, если удается узнать вид функции и значения аргументов. Одной из основных задач обработки результатов эксперимента является выявление, оценка величины и, по возможности, устранение всех систематических погрешностей. Изменяющиеся систематические погрешности выявляются легче постоянных. Для выявления постоянной систематической погрешности необходимо выполнить измерения хотя бы двумя различными способами или методами. Обнаруженные и оцененные систематические погрешности исключаются из результатов путем введения поправок. В зависимости от причин возникновения систематические погрешности подразделяют на следующие виды: 1. Погрешности метода или модели, которые обычно называют методическими погрешностями, например: определение плотности вещества без учета имеющихся в нем примесей, использование формул, не совсем точно описывающих явление, и др. 2. Погрешности воздействиявнешних факторов: внешних тепловых, радиационных, гравитационных, электрических и магнитных полей. 3. Погрешности, возникающие из-за неточности действий или личных качеств оператора (экспериментатора), называемые субъективными погрешностями. 4. Инструментальные (приборные, аппаратурные) погрешности, обусловленные схемными, конструктивными и технологическими несовершенствами средств измерения, их состоянием в процессе эксплуатации. Например, смещение начала отсчета, неточность градуировки шкалы прибора, использование прибора вне допустимых пределов его эксплуатации, неправильное положение прибора и т. п. За исключением смещения начала отсчета, приборные погрешности относятся к разряду неустранимых погрешностей. В общем случае систематическая погрешность обусловлена суммарным воздействием перечисленных факторов, многие из которых невозможно рассчитать, подавить или выявить в данном эксперименте. Самым простым способом выявления суммарной систематической погрешности было бы сопоставление результатов измерений, полученных с помощью серийного (рабочего) и более точного образцового приборов. Разность результатов измерений даст суммарную систематическую погрешность, вносимую серийным прибором в результат измерения. Однако такой способ выявления систематической погрешности является слишком дорогим. Поэтому на практике различные составляющие систематической погрешности пытаются устранить с помощью экспериментальных или математических приемов путем введения поправок в результаты наблюдений при условии, что погрешность данного вида по величине и знаку известна. После внесения поправок влияние систематической погрешности данного вида на результат и погрешность измерения устраняется полностью. Если же систематическая погрешность неизвестна, но имеет известные границы изменения, то её учитывают в результате измерения. В зависимости от характера измерения систематические погрешности подразделяют на элементарные и изменяющиеся по сложному закону. Элементарные погрешности можно условно разделить на постоянные, прогрессирующие (прогрессивные) и периодические. Прогрессирующими называют монотонно возрастающие или монотонно убывающие погрешности. Периодические погрешности – погрешности, изменение которых можно описать периодической функцией. Погрешности, изменяющиеся по сложному закону, образуются при объединении нескольких систематических погрешностей. Постоянные систематические погрешности представлены в графической форме на рисунке 3.2 а (  , или  ), а переменные – на рисунке 3.2 б – е. Простейшие переменные систематические погрешности, которые аппроксимируют графиками без перегибов (монотонно изменяющиеся или прогрессирующие) показаны на рисунке 3.2 б – г, а периодические или гармонические погрешности – на рисунке 3.2 е.Всем известны "спешащие" и "отстающие" часы, погрешности которых прогрессируют во времени, но мало кто анализирует показания часов за полный оборот стрелки. Если оценивать погрешности, то можно утверждать, что в результате многократного повторения вращения стрелки часов должны проявляться периодические погрешности, обусловленные эксцентриситетом и превращающиеся в нуль при завершении каждого полного оборота.    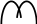 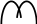  Рисунок 3.2 - Виды простейших систематических погрешностей: а – постоянные, б, в – прогрессирующие (линейная и нелинейная), г, д – прогрессирующие нелинейные (предложены варианты аппроксимации прямыми линиями), е – периодические (гармонические). Обычно для описания и для аппроксимации систематической погрешности подбирают наиболее простую функцию, например линейную для прогрессирующей погрешности. Такой же упрощенный подход применяют и для аппроксимации гармонической систематической погрешности, которая может быть описана как синусоида, косинусоида, пилообразная либо другая периодическая функция. Систематическая погрешность может иметь не только элементарный, но и более сложный характер, который можно аппроксимировать функцией, включающей приведенные простые составляющие. Сложная систематическая погрешность, включающая постоянную, прогрессирующую и периодическую составляющую, в общем виде может быть описана выражением  , где  – постоянная составляющая сложной систематической погрешности;  – соответственно аргументы прогрессирующей и периодической составляющих сложной систематической погрешности.3.3 Случайная погрешность Случайная погрешность – это составляющая погрешности измерения, проявляющаяся в виде непредсказуемых отклонений от истинного значения физической величины, меняющихся от одного наблюдения к другому. Данная погрешность обусловлена влиянием на результаты измерения множества факторов, воздействие которых на каждое отдельное измерение невозможно учесть или заранее предсказать. Такими причинами могут быть перепады напряжения в сети, вибрация установки, изменения атмосферного давления, температуры, электрических, магнитных и радиационных полей, а также ошибки, связанные с действиями самого экспериментатора (неправильное считывание показаний приборов, различная скорость реакции и т. п.). Случайную погрешность нельзя исключить из результатов измерений, однако, пользуясь статистическими методами, можно учесть её влияние на оценку истинного значения измеряемой величины. В процессе измерения оба вида погрешностей проявляются одновременно, и погрешность измерения можно представить в виде суммы: изм = + где - случайная, а - систематическая погрешности. Полная погрешность измерения, являющаяся суммой указанных составляющих, может быть представлена в абсолютном, относительном или нормированном виде. Абсолютная погрешность – это погрешность измерения, выраженная в единицах измеряемой величины. Наряду с абсолютной погрешностью часто используется термин абсолютное значение погрешности, под которым понимают значение погрешности без учета ее знака. Эти два понятия различны. Абсолютнаяпогрешность определяется как разность  или  Относительная погрешность – это погрешность измерения, выраженная отношением абсолютной погрешности к результату измерения:  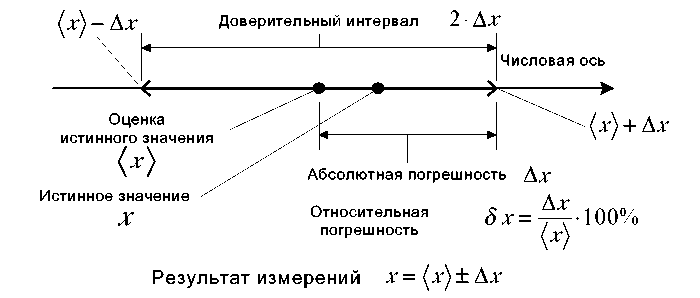 Приведенная погрешность – это погрешность, выраженная отношением абсолютной погрешности средства измерения (приборной погрешности) к некоторой постоянной величине, называемой нормирующим значением и имеющей размерность измеряемой величины. γ = ± (Δ/xN )100%, где xN – нормированное значение величины. В качестве нормирующего множителя может выступать, например, максимальное значение шкалы прибора (верхний предел показаний прибора). Понятие приведенной погрешности относится только к средствам измерений. 3.4 Грубые погрешности и промахи. Статические и динамические погрешности Погрешности, которые нельзя отнести ни к случайным, ни к систематическим из-за совершенно иного механизма образования и принципиально отличного значения, называют грубыми погрешностями измерений или промахами. Грубая погрешность – погрешность измерения, значительно превышающая погрешности большинства результатов наблюдений. Такие погрешности могут возникать вследствие резкого изменения внешних условий эксперимента: внезапного изменения температуры, напряжения в сети и т. п. Грубые погрешности обнаруживают статистическими методами и соответствующие результаты измерений, как не отражающие закономерностей поведения измеряемой величины, исключают из рассмотрения. Промах – это вид грубой погрешности, зависящий от наблюдателя и связанный с неправильным обращением со средствами измерений: неверными отсчетами показаний приборов, описками при записи результатов, невнимательностью экспериментатора, путаницей номеров образцов и т. п. Промахи обнаруживают нестатистическими методами и результаты наблюдений, содержащие промахи, как заведомо неправильные, исключают из рассмотрения. Указанные составляющие, как правило, не зависят друг от друга, что допускает их раздельное рассмотрение. Очевидно, что причинами возникновения грубой погрешности могут быть промах оператора при снятии отсчета или его записи, ошибка в реализации методики измерений, сбой в измерительной цепи прибора или незамеченное импульсное изменение влияющей физической величины. Причины появления результатов с грубыми погрешностями резко выпадают из ряда механизмов, формирующих систематические или случайные составляющие погрешности измерений. В зависимости от режима измерения погрешности принято делить на статические и динамические. Статическая погрешность измерений (статическая погрешность) – погрешность результата измерений, свойственная условиям статического измерения.Динамическая погрешность измерений (динамическая погрешность) – погрешность результата измерений, свойственная условиям динамического измерения. Динамической погрешностью средства измерений называется составляющая погрешности, дополнительная к статической, и возникающая при измерении в динамическом режиме. В соответствии с определением  , где  – динамическая погрешность средства измерения;  – погрешность средства измерения при использовании его в динамическом режиме;  – статическая погрешность средства измерения (погрешность при использовании средства измерений в статическом режиме).Логически обоснованной представляется следующая укрупненная классификация погрешностей измерений по степени полноты информации об их характере и значениях: определенные погрешности, неопределенные погрешности. К определенным можно отнести любые известные по числовому значению и знаку погрешности. Известными могут стать, например те составляющие погрешности измерений, которые имеют достаточно жесткую функциональную связь с вызывающими их аргументами. Такие погрешности по сути совпадают с систематическими и принципиально могут быть выявлены и исключены из результатов измерений, их значения можно прогнозировать. Определенной можно считать также любую (в том числе и уже зафиксированную случайную или даже грубую) погрешность, числовое значение и знак которой получены экспериментальными методами. Определенные погрешности в при достаточной полноте информации могут быть исключены из результатов измерений. Теоретическая определенность систематических погрешностей делает возможным исключение этих погрешностей до измерений, в процессе измерений, а также при математической обработке результатов измерительного эксперимента после выполнения измерений. К неопределенным погрешностям следует отнести невыявленные систематические, а также погрешности случайные (собственно случайные) и грубые погрешности, значения которых не были определены экспериментально. При исключении определенных погрешностей абсолютная точность невозможна, поэтому приходится относить к неопределенным неисключенные остатки погрешностей. Неисключенная систематическая погрешность – составляющая погрешности результата измерений, обусловленная погрешностями вычисления и введения поправок на влияние систематических погрешностей или систематической погрешностью, поправка на действие которой не введена вследствие ее малости . Систематическими составляющими, значения которых существенно меньше случайных погрешностей (  ), пренебрегают. Такие погрешности относят к пренебрежимо малым неисключенным систематическим составляющим погрешности измерения. |