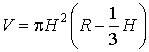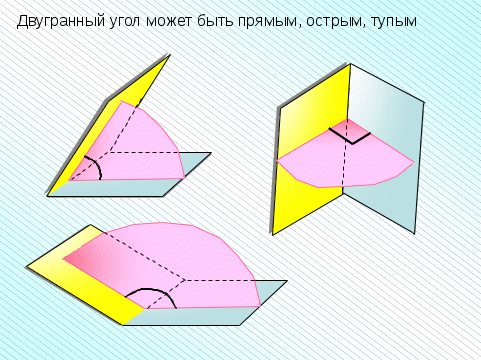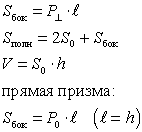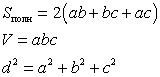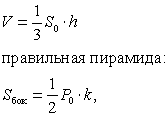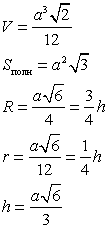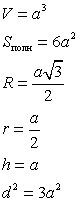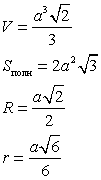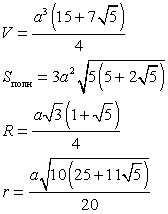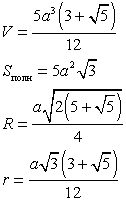Дисциплина: Геометрия
Лекция 4: Стереометрия
I. Основные понятия и аксиомы стереометрии. Параллельность прямых и плоскостей
1.1. Аксиомы стереометрии и их следствия.
1.2. Параллельные прямые в пространстве.
1.3. Параллельность прямой и плоскости.
1.4. Параллельность плоскостей.
II. Перпендикулярность прямых и плоскостей.
2.1. Перпендикуляр и наклонная.
2.2. Перпендикулярные плоскости
III. Двугранный угол
IV . Многогранники
4.1 Правильные многогранники
Глава I. «Основные понятия и аксиомы стереометрии.
Параллельность прямых и плоскостей»
Стереометрия — это раздел геометрии, в котором изучаются свойства фигур в пространстве.
Слово «стереометрия» происходит от греческих слов «στερεοσ» — объемный, пространственный и «μετρεο» — измерять.
Простейшие фигуры в пространстве: точка, прямая, плоскость.
Плоскость.
Представление о плоскости дает гладкая поверхность стола или стены. Плоскость как геометрическую фигуру следует представлять себе простирающейся неограниченно во все стороны.
|

|
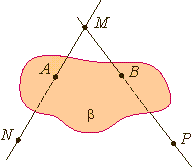
На рисунках плоскости изображаются в виде параллелограмма или в виде произвольной области и обозначаются греческими буквами α, β, γ и т.д.
Точки А и В лежат в плоскости β (плоскость β проходит через эти точки), а точки M, N, P не лежат в этой плоскости. Коротко это записывают так: А ∈ β, B ∈ β,
|
|
1.1 Аксиомы стереометрии и их следствия.
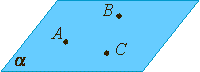
Аксиома 1.
Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
|
|
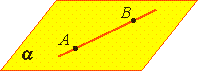
Аксиома 2.
Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости. (Прямая лежит на плоскости или плоскость проходит через прямую).
|
|
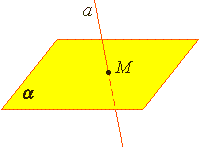
Из аксиомы 2 следует, что если прямая не лежит в данной плоскости, то она имеет с ней не более одной общей точки. Если прямая и плоскость имеют одну общую точку, то говорят, что они пересекаются.
|
|
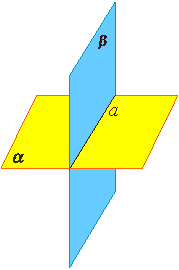
Аксиома 3.
Если две различные плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей. В таком случае говорят, плоскости пересекаются по прямой.
Пример: пересечение двух смежных стен, стены и потолка комнаты.
|
|
Некоторые следствия из аксиом
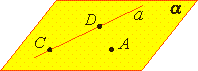
Теорема 1.
Через прямую a и не лежащую на ней точку А проходит плоскость, и притом только одна.
|
|
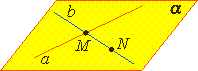
Теорема 2.
Через две пересекающиеся прямые a и b проходит плоскость, и при том только одна.
|
|
1.2 Параллельные прямые в пространстве.
Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
|
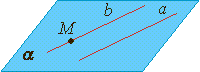
Теорема о параллельных прямых.
Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.
|
|
Лемма о пересечении плоскости параллельными прямыми.
Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.
|
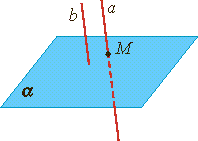
|
Теорема о трех прямых в пространстве.
Если две прямые параллельны третьей прямой, то они параллельны (если a∥c и b∥c, то a∥b).
|
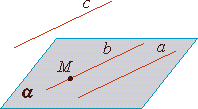
|
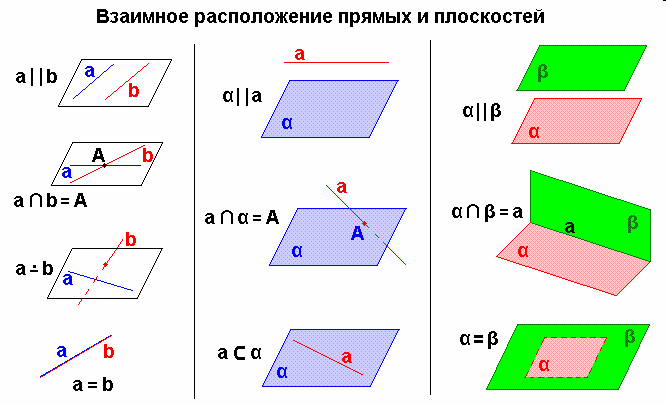
Взаимное расположение прямых в пространстве
|
Пересекающиеся прямые:
лежат в одной плоскости, имеют одну общую точку.
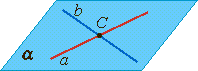
|
Параллельные прямые:
лежат в одной плоскости, не имеют общих точек (не пересекаются)
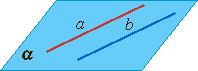
|
Скрещивающиеся прямые:
не лежат в одной плоскости, не имеют общих точек (не пересекаются)
|
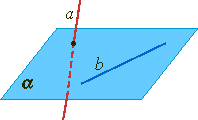
1.3 Параллельность прямой и плоскости.
Прямая и плоскость называются параллельными, если они не имеют общих точек.
|
Признак параллельности прямой и плоскости
Теорема.
Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.
|
|
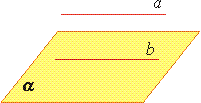
Теорема.
Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.
|
|
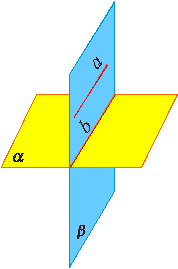
Теорема.
Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо также параллельна данной плоскости, либо лежит в этой плоскости.
|
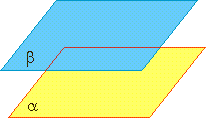
1.4 Параллельность плоскостей.
Две плоскости называются параллельными, если они не пересекаются, т.е. не имеют ни одной общей точки. α∥β.
|
|
Признак параллельности двух плоскостей
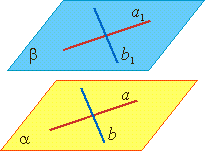
Теорема. Если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости , то эти плоскости параллельны.
Если а∥а1 и b∥b1, то α∥β.
|
| | |
Если α∥β и они пересекаются с γ, то а∥b.
Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.
Если α∥β и AB∥CD, то АВ = CD.
Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны.
|
|
Глава II. Перпендикулярность прямых и плоскостей.
|
Определение
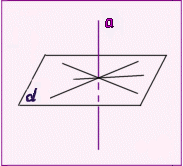
Прямая, пересекающая плоскость, называется перпендикулярной этой плоскости, если она перпендикулярна каждой прямой, которая лежит в данной плоскости и проходит через точку пересечения.
|
|
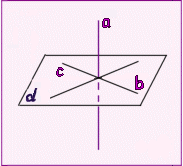
Теорема (ПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ ПРЯМОЙ И ПЛОСКОСТИ).
Если прямая, пересекающая плоскость, перпендикулярна двум прямым в этой плоскости, проходящим через точку пересечения данной прямой и плоскости, то она перпендикулярна плоскости.
|
|
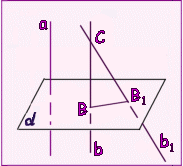
Теорема. Если плоскость перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой.
|
|
Теорема. Две прямые, перпендикулярные одной и той же плоскости, параллельны.
|
|
2.1 Перпендикуляр и наклонная.
|
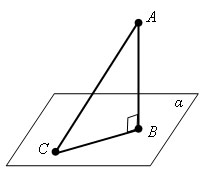
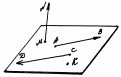
Перпендикуляром, опущенным из данной точки данную плоскость, называется отрезок, соединяющий данную точку с точкой плоскости и лежащий на прямой, перпендикулярной плоскости. Конец этого отрезка, лежащий в плоскости, называется основанием перпендикуляра.
Наклонной, проведенной из данной точки к данной плоскости, называется любой отрезок, соединяющий данную точку с точкой плоскости, не являющийся перпендикуляром к плоскости. Конец отрезка, лежащий в плоскости, называется основанием наклонной.
Отрезок, соединяющий основания перпендикуляра наклонной, проведенных из одной и той же точки, называется проекцией наклонной.
AB – перпендикуляр к плоскости α.
AC – наклонная, CB – проекция.
С – основание наклонной, B - основание перпендикуляра.
|
|
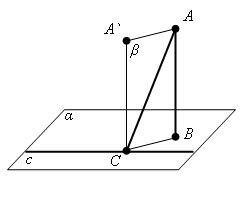
Теорема о трех перпендикулярах
Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна ее проекции, то она перпендикулярна наклонной.
|
|
Обратная теорема о трех перпендикулярах
Если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной.
|

|
Перпендикулярные плоскости
|
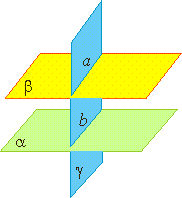
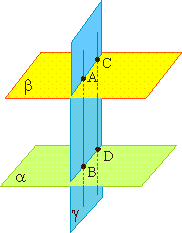
Две пересекающиеся плоскости называются перпендикулярными, если третья плоскость, перпендикулярная прямой пересечения этих плоскостей, пересекает их по перпендикулярным прямым.
Плоскость α перпендикулярна плоскости β. Они пересекаются по прямой с. Плоскость γ перпендикулярна с и пересекает плоскости α и β по прямым a и b соответственно.
|
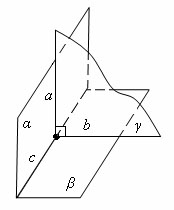
|
Признак перпендикулярности плоскостей
Теорема. Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
|
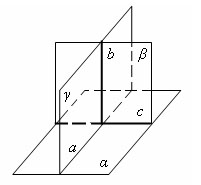
|
Расстояние между скрещивающимися прямыми
Общим перпендикуляром двух скрещивающихся прямых называется отрезок с концами на этих прямых, являющийся перпендикуляром к каждой из них.
Расстоянием между скрещивающимися прямыми называется длина их общего перпендикуляра. Оно равно расстоянию между параллельными плоскостями, проходящими через эти прямые.
|
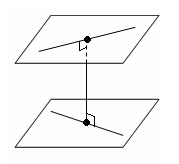
|
Расстояние между скрещивающимися прямыми.
Теорема. Две скрещивающиеся прямые имеют общий перпендикуляр, и при том только один. Он является общим перпендикуляром параллельных плоскостей, проходящих через эти прямые.
|
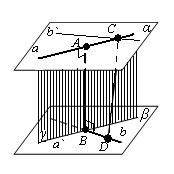
|
|
Глава III. Двугранный угол
Двугранным углом называется фигура, образованная двумя плоскостями с общей ограничивающей их прямой.
Полуплоскостиназываются гранями, а ограничивающая их прямая – ребром двухгранного угла.
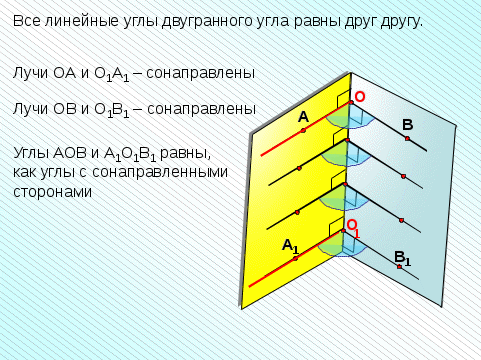
Плоскость, перпендикулярная ребру двухгранного угла, пересекает его грани по двум полупрямым.
Угол, образованный этими полупрямыми, называется линейным углом двухгранного угла.
|
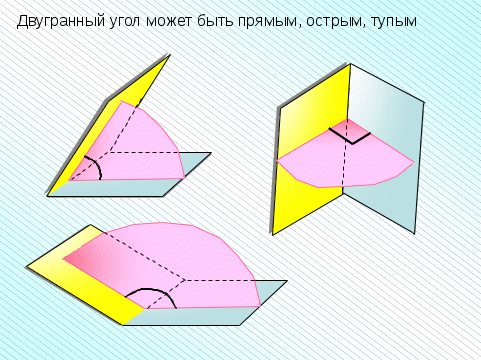
|

|
|
Глава IV. Многогранники
Обозначения:
V — объем;
Sполн — площадь полной поверхности;
Sбок — площадь боковой поверхности;
Sо — площадь основания;
Pо — периметр основания;
Pо — периметр перпендикулярного сечения;
l — длина ребра;
h — высота.
|
Формула Эйлера: N − L + F = 2 ; N — число вершин, L — число ребер, F — число граней выпуклого многогранника.
|
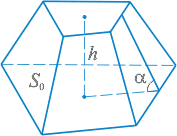
Призма — многогранник, две грани которого — равные многоугольники, расположенные в параллельных плоскостях, а остальные — параллелограммы.
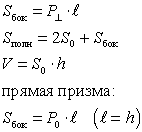
|
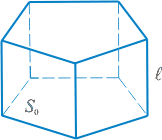
|
Параллелепипед — призма, основание которой — параллелограмм.
Параллелепипед имеет шесть граней и все они — параллелограммы.
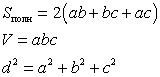
|
|
Пирамида — многогранник, у которого одна грань n-угольник — основание пирамиды, а остальные боковые грани — треугольники с общей вершиной — вершиной пирамиды.
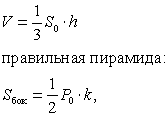
|
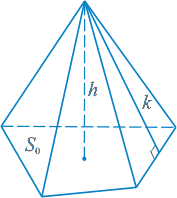
|
Если в пирамиде провести сечение параллельное основанию, то тело, ограниченное этим сечением, основанием, и заключенной между ними боковой поверхностью пирамиды, называется усеченной пирамидой.
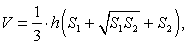
где S1 и S2 — площади оснований
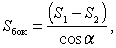 где α — двугранный угол при ребре нижнего основания. где α — двугранный угол при ребре нижнего основания.
|
|
4.1. Правильные многогранники
|
Многогранник называется правильным, если все его грани — равные правильные многоугольники, а все многогранные углы имеют одинаковое число граней.
Все ребра правильного многогранника — равные отрезки, все плоские углы правильного многогранника также равны.
Существует пять различных правильных многогранников (выпуклых): правильный четырехгранник (правильный тетраэдр), правильный шестигранник (куб), правильный восьмигранник (правильный октаэдр), правильный двенадцатигранник (правильный додекаэдр), правильный двадцатигранник (правильный икосаэдр).
|
Обозначения:
а — длина ребра;
V — объем;
Sбок — площадь боковой поверхности;
Sполн — площадь полной поверхности;
R — радиус описанной сферы;
r — радиус вписанной сферы;
h — высота.
|
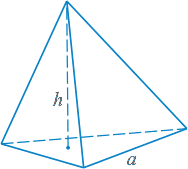
Тетраэдр — четыре грани — равносторонние равные треугольники. Тетраэдр имеет четыре вершины и шесть ребер
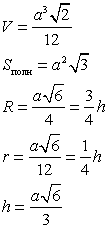
|
|
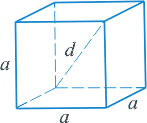
Куб — шесть граней — равные квадраты. Куб имеет восемь вершин и двенадцать ребер.
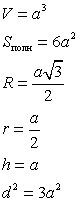
|
|
Октаэдр — восемь граней — равносторонние равные треугольники. Октаэдр имеет шесть вершин и двенадцать ребер
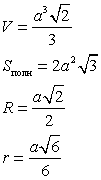
|
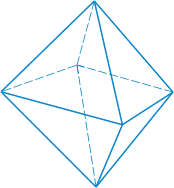
|
Додекаэдр — двенадцать граней — правильные равные пятиугольники. Додекаэдр имеет двадцать вершин и тридцать ребер.
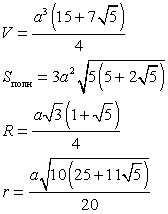
|
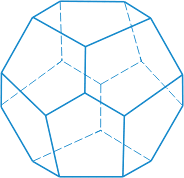
|
Икосаэдр — двадцать граней — равносторонние равные треугольники. Икосаэдр имеет двенадцать вершин и тридцать ребер.
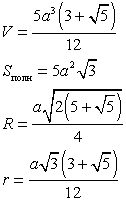
|
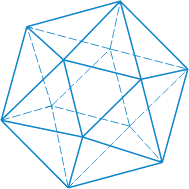
|
Глава IV. Векторы в пространстве.
Вектором называется отрезок, для которого указано, какой из его концов считается началом, а какой - концом. Любая точка пространства рассматривается как нулевой вектор.
 - нулевой вектор, обозначается - нулевой вектор, обозначается  . .
Длина вектора 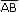 обозначается | обозначается |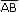 |. |.
Два ненулевых вектора называются коллинеарными, если они лежат на одной или на параллельных прямых.
|
|
Векторы называются равными, если они сонаправлены и их длины равны.
От любой точки можно отложить вектор, равный данному, и притом только один.
|
|
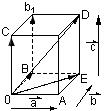
5.1 Действия над векторами.
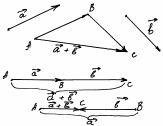
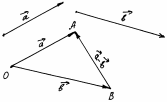
1. Сложение векторов по правилу треугольника:
|
для этого нужно от произвольной точки пространства отложить вектор 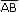 , равный , равный 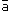 , затем от точки В отложить вектор , затем от точки В отложить вектор 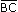 , равный , равный 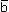 . .
Вектор 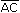 называется суммой называется суммой 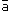 и и 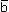 . .
Таким образом 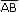 + +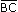 = =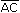 , для любых трех точек А, В , для любых трех точек А, В
|
|
|
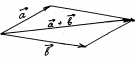
2. Сложение векторов по правилу параллелограмма:
для этого векторы откладывают от одной точки.
Два ненулевых вектора называются противоположными, если их длины равны и они противоположно направлены.
|
|
3. Вычитание векторов:
Разностью векторов 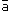 и и 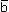 называется такой вектор, сумма которого с вектором называется такой вектор, сумма которого с вектором 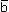 равна вектору равна вектору 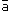 . .
Разность 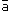 - - 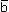 можно найти по формуле можно найти по формуле 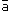 - - 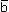 = = 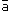 + (- + (-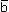 ), где (- ), где (-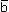 ) - вектор, противоположный вектору ) - вектор, противоположный вектору 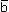 . .
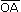 - - = =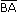 . .
|
Сумма нескольких векторов в пространстве вычисляется так же, как и на плоскости и не зависит от порядка слагаемых.
|
|
Умножение вектора на число.
Произведением ненулевого вектора 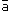 на число k называется такой вектор на число k называется такой вектор 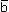 , длина которого равна |k|·| , длина которого равна |k|·|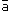 | |
Лемма. Если векторы 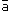 и и 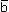 коллинеарны и вектор коллинеарны и вектор 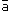 не равен нулевому вектору, то существует число k такое, что вектор не равен нулевому вектору, то существует число k такое, что вектор 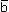 равен k равен k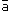 . .
Векторы называются компланарными, если при откладывании от одной и той же точки они будут лежать в одной плоскости.
Теорема. Любой вектор можно разложить по трём данным некомпланарным векторам, причём коэффициенты разложения определяются единственным образом.
Если 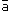 , , 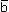 , , 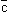 - некомпланарные векторы, то любой вектор - некомпланарные векторы, то любой вектор 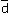 можно представить в виде: можно представить в виде:
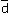 = х = х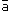 + у + у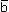 + z + z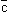 , ,
где х, у, z - числа.
|
|
Объемы и площади поверхностей тел
Наклонная призма
Объем наклонной призмы
V=Sпсa,
где Sпс - площадь перпендикулярного сечения наклонной призмы, a - боковое ребро.
Площадь боковой поверхности наклонной призмы
Sб=Pпсa,
где Pпс - периметр перпендикулярного сечения наклонной призмы, a - боковое ребро.
Площадь полной поверхности наклонной призмы
ЗSп=Sб+2Sосн,
где Sб, - площадь боковой поверхности наклонной призмы, Sосн - площадь её основания.
Прямая призма
Объем прямой призмы
V=Sоснa,
где Sосн - площадь основания прямой призмы, a - боковое ребро.
Площадь боковой поверхности прямой призмы
Sб=Pоснa,
где Pосн - периметр основания прямой призмы, a - боковое ребро.
Площадь полной поверхности прямой призмы
Sп=Sб+2Sосн,
где Sб, - площадь боковой поверхности прямой призмы, Sосн - площадь основания.
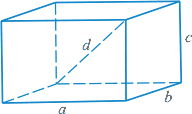
Прямоугольный параллелепипед
Объем прямоугольного параллелепипеда
V=abc,
где a,b,c - измерения прямоугольного параллелепипеда.
Площадь боковой поверхности параллелепипеда
Sб=2c(a+b),
где a, b - стороны основания, c - боковое ребро прямоугольного параллелепипеда.
А Площадь полной поверхности прямоугольного параллелепипеда
Sп=2(ab+bc+ac),
где a,b,c - измерения прямоугольного параллелепипеда.
Куб
V=a3, Sб=4a2, Sп=6a2,
где a - ребро куба.
Пирамида
Объем пирамиды
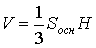
где Sосн - площадь основания, H - высота.
Площадь боковой поверхности пирамиды равна сумме площадей её боковых граней.
Площадь полной поверхности пирамиды
Sп=Sб+2Sосн,
где Sб - площадь боковой поверхности прямой пирамиды, Sосн - площадь основания.
Площадь боковой поверхности правильной пирамиды
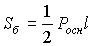
где Pосн - периметр основания правильной пирамиды, l - её апофема.
Усеченная пирамида
Объем усеченной пирамиды
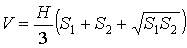
где S1 , S2 - площади оснований усеченной пирамиды, H - её высота.
Площадь боковой поверхности усеченной пирамиды равна сумме площадей ее боковых граней.
Площадь полной поверхности усеченной пирамиды
Sп=Sб+S1+S2 ,
где Sб- площадь боковой поверхности пирамиды, S1 , S2 - площади оснований.
Площадь боковой поверхности правильной усеченной пирамиды
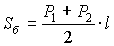
где P1 , P2 - периметры оснований, а l - ее апофема.
Цилиндр
Объем цилиндра
V=p R 2H ,
где R - радиус основания цилиндра, а H - его высота.
Площадь боковой поверхности цилиндра
Sб=2p R H ,
где R - радиус основания цилиндра, а H - его высота.
Площадь полной поверхности цилиндра
Sп=2p R H + 2p R2,
где R - радиус основания цилиндра, а H - его высота.
КЛЮЧЕНИЕ
Конус
Объем конуса
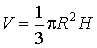
где R - радиус основания конуса, а H - его высота.
Площадь боковой поверхности конуса.
Sб=2p R L ,
где R - радиус основания конуса, а L - его образующая.
Площадь полной поверхности конуса
Sп=2p R (R+L),
где R - радиус основания конуса, а L - его образующая.
Усеченный конус
Объем усеченного конуса
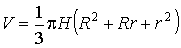
где R, r - радиусы оснований усеченного конуса, Н - его высота.
Площадь боковой поверхности усеченного конуса
Sб=p L (R+r),
где R, r - радиусы оснований усеченного конуса, L - его образующая.
Площадь полной поверхности усеченного конуса
Sп=p L (R+r)+p R2+p r2,
где R, r - радиусы оснований усеченного конуса, L - его образующая.
Сфера и шар
Объем шара
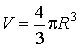
где R - радиус шара.
Площадь сферы (площадь поверхности шара)
S=4p R2,
где R - радиус сферы.
Объем шарового сегмента
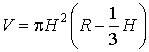
где H - высота шарового сегмента, R - радиус шара.
Объем шарового сектора
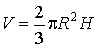
где H - высота соответствующего шарового сектора, R - радиус шара.
СПИСОК ЛИТЕРАТУРЫ
Основная литература.
Геометрия 10-11: Учеб. для общеобразоват. учреждений/ Л.С.Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – М.: Просвещение, 2009.
Дополнительная литература:
Ю.А. Глазков, И.И. Юдина, В.Ф. Бутузов. Рабочая тетрадь по геометрии для 10 класса. – М.: Просвещение, 2010.
В.Ф. Бутузов, Ю.А. Глазков, И.И. Юдина. Рабочая тетрадь по геометрии для 11 класса. – М.: Просвещение, 2010.
|
 Скачать 0.97 Mb.
Скачать 0.97 Mb.