Методы диагностирования подшипников. 5-ЛЕКЦИЯ.МЕТОДЫ СТД ПОДШ. Лекция. 5 методы вибродиагностирования подшипников качения
 Скачать 337.69 Kb. Скачать 337.69 Kb.
|
|
ЛЕКЦИЯ.5 «МЕТОДЫ ВИБРОДИАГНОСТИРОВАНИЯ ПОДШИПНИКОВ КАЧЕНИЯ»
П л а н л е к ц и и Введение. Диагностирование подшипников качения. Метод пик-фактора. Метод прямого спектра. Метод спектра огибающей. Метод ударных импульсов. Сравнительные характеристики методов диагностирования. Заключение. Контрольные вопросы. Введение Подшипник качения является, пожалуй, наиболее распространенным элементом конструкции любого роторного механизма и, в то же время, наиболее уязвимым элементом. Подшипники осуществляют пространственную фиксацию вращающихся роторов и, следовательно, именно подшипники воспринимают большую часть статических и динамических усилий, возникающих в работающем механизме. Состояние подшипников является важнейшей составляющей технического состояния механизма, его исправности и работоспособности. Не хочется утомлять читателя банальными истинами, для любого эксплуатационника, очевидно, что если и надо заниматься где-то вибродиагностикой, то в первую очередь необходимо решать эту задачу для подшипников. Именно так обстоит дело и в действительности. Вибродиагностика состояния подшипников качения является в настоящее время одной из наиболее развитых, разработанных областей виброметрии как в теоретическом плане, так и в плане практической аппаратурной реализации. Вибродиагностика подшипников качения является прекрасной иллюстрацией того, как можно диагностировать один и тот же узел различными методами, основанными на различных вибрационных процессах, генерируемых дефектами этого узла. В настоящее время в вибродиагностике используются, по крайней мере, четыре метода оценки технического состояния подшипников качения, которые обычно называют следующим образом: метод ПИК-фактора; метод прямого спектра; метод спектра огибающей; метод ударных импульсов. Ниже кратко изложен физический смысл получения вибродиагностических параметров каждым из этих методов. Диагностирование подшипников качения Метод ПИК-фактора Если мы установим акселерометр вблизи наружной обоймы исправного, хорошо смазанного подшипника и посмотрим полученный сигнал на осциллографе, мы увидим стационарный двухполярный сигнал шумового характера, симметричный относительно временной оси, как это примерно показано на рис. 7.1, а. 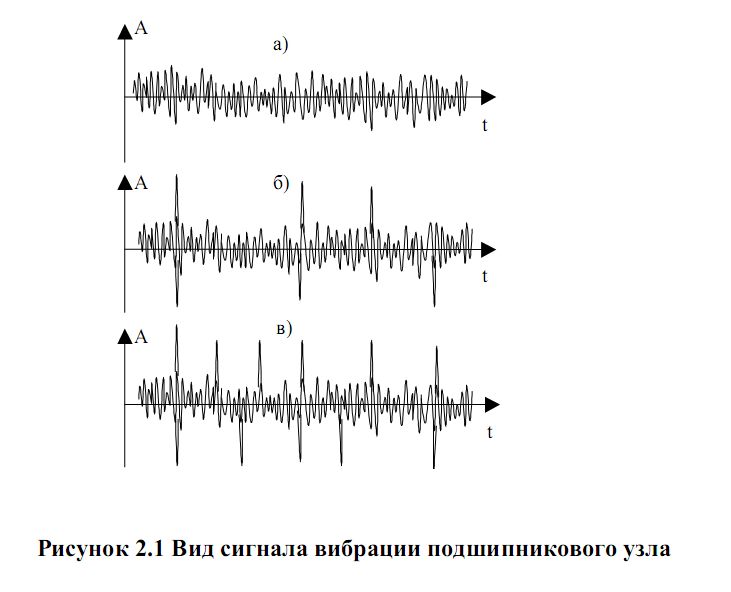 Рис. 7.1. Вил сигнала вибрации подшипникового узла Пусть в нашем распоряжении есть простой виброметр, позволяющий измерять два параметра вибросигнала: среднеквадратичное значение уровня (СКЗ) вибрации, т.е. энергию вибрации; пиковую амплитуду (ПИК) вибрации (положительную, отрицательную или полный размах – значения не имеет). Будем измерять два этих параметра в процессе эксплуатации подшипника с обычной периодичностью примерно 1 раз в 2-3 месяца. С течением времени, по мере появления дефектов на кинематических узлах подшипника, в вибросигнале начнут появляться отдельные, короткие амплитудные пики, соответствующие моментам соударения дефектов, рис. 7.1, б. В дальнейшем, с развитием дефекта, сначала увеличиваются амплитуды пиков, потом постепенно увеличивается и их количество, рис. 7.1, в, - дефект начинает «разноситься» по подшипнику, т.е. появившись вначале, например, на одном из шариков, он создаёт, в конце концов, забоину на кольце, с него она переносится на другой шарик, дефекты шариков начинают вырабатывать сепаратор и т.д. до полного разрушения. Если изобразить результаты измерений на графике, мы увидим зависимости, показанные на рис. 7.2. ПИК и СКЗ представляют собой монотонные, неубывающие функции одинакового характера, но смещённые друг относительно друга во времени. Сначала, по мере появления и развития дефекта, нарастает функция ПИК, а СКЗ меняется очень мало, поскольку отдельные, очень короткие амплитудные пики практически не меняют энергетические характеристики сигнала. 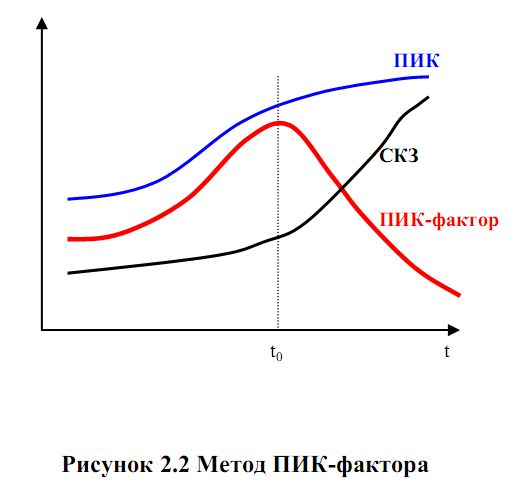 Рис. 7.2. Метод ПИК-фактора В дальнейшем, по мере увеличения и количества пиков, начинает уже соответственно увеличиваться энергия сигнала, возрастает СКЗ вибрации. Сами по себе функции ПИК и СКЗ малоинформативны для диагностики, вследствие своей монотонности. Но отношение ПИК/СКЗ, называемое ПИК-фактором, уже представляет значительный интерес, поскольку эта функция из-за временного сдвига между ПИК и СКЗ, имеет явно выраженный максимум на временной оси. На этом и основывается метод ПИК-фактора. Экспериментально было установлено, что момент прохода функции ПИК-фактор через максимум соответствует остаточному ресурсу подшипника порядка 2-3 недель. Каковы достоинства и недостатки этого метода? Основное достоинство – простота. Для его реализации нужен обычный виброметр общего уровня, т.е. самый простой и дешёвый виброизмерительный прибор. Основные недостатки – слабая помехозащищенность метода и необходимость проводить многократные измерения в процессе эксплуатации. Дело в том, что установить датчик непосредственно на наружной обойме подшипника практически невозможно, т.е. он устанавливается где-то на корпусе механизма. Значит и сигнал вибрации характеризует не только подшипник, но и другие узлы механизма, что в данном случае можно рассматривать как вибрационные помехи. И чем дальше установлен датчик от подшипника и сложнее кинематика самого механизма, тем меньше достоверность метода. Поэтому и использовать метод, в первую очередь, целесообразно тогда, когда датчик можно расположить близко к подшипнику и сама кинематика механизма проста. Например, подшипниковые узлы различных распределительных устройств в технологическом оборудовании, подшипники вентиляторов и пр. Во-вторых, для получения достоверной оценки необходимо многократно проводить измерения при эксплуатации. Получить оценку состояния по одному замеру невозможно. Исключения возможны только тогда, когда речь идёт о вибродиагностике большого количества совершенно одинаковых механизмов, эксплуатирующихся в одинаковых условиях. Метод прямого спектра Вернёмся к вибрационным сигналам, показанным на рис. 7.1. Те же самые сигналы можно проанализировать не только с точки зрения соотношения амплитудных и энергетических характеристик, но и с точки зрения периодичности появления амплитудных всплесков. Именно на этом и базируется метод прямого спектра. Вибрационный сигнал анализируется узкополосным спектроанализатором и по частотному составу спектра можно идентифицировать возникновение и развитие дефектов подшипника. 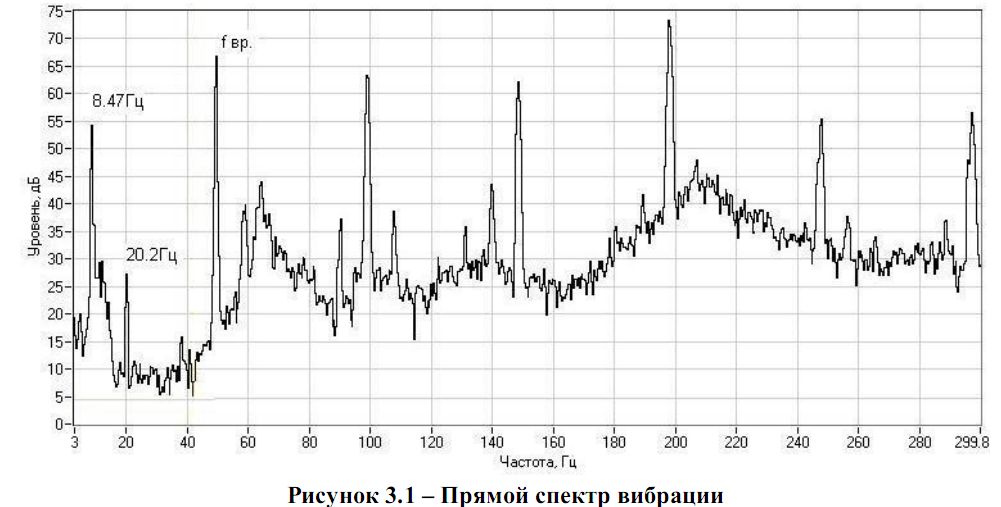 Рис. 7.3. Прямой спектр вибраций Амплитудные всплески в вибросигнале следуют не хаотично, а с вполне определённой периодичностью или частотой. Причём дефекту на каждом из элементов подшипника (тела качения, дорожки, сепаратор) соответствуют свои частоты, которые однозначно просчитываются в зависимости от кинематики подшипника и скорости его вращения. Наличие той или иной дискретной составляющей в спектре сигнала говорит о возникновении соответствующего дефекта подшипника, а амплитуда этой составляющей – о глубине дефекта. Это несколько упрощённый подход, поскольку многие дефекты в спектре проявляются в виде не одной частотной составляющей, а нескольких, но мы не будем здесь вдаваться в тонкости спектрального анализа сложных сигналов. К пониманию сути метода это мало что добавит. Очевидно, что основных достоинств у метода два: достаточно высокая помехозащищённость (маловероятно наличие в механизме источников, создающих вибрации на тех же точно частотах, что и дефекты подшипника); информативность метода существенно выше, чем по методу ПИК-фактора. Вы имеете возможность получить дифференцированную оценку состояния подшипника отдельно по каждому его кинематическому узлу, поскольку они генерируют разные частотные ряды в спектре. Недостатков, к сожалению, тоже, как минимум, два: метод дорогостоящий, любой самый простенький узкополосный спектроанализатор стоит неизмеримо дороже самого «навороченного» виброметра; метод малочувствителен к зарождающимся и слабым дефектам. Это связано с тем, что подшипник в подавляющем большинстве механизмов является очень маломощным источником вибрации. Другими словами, небольшой скол на шарике или дорожке не в состоянии заметно качнуть механизм, чтобы мы увидели эту частотную составляющую в спектре вибрации. И только при достаточно сильных дефектах амплитуды этих частотных составляющих начинают заметно выделяться над общей шумовой частью спектра. Несмотря на эти недостатки метод используется достаточно широко, особенно в среде профессиональных специалистов и даёт хорошие результаты. Метод спектра огибающей Исходный вибросигнал, естественно, у нас всё тот же, так что вернёмся ещё раз к рис. 7.1. Обратим теперь внимание на то, что высокочастотная, шумовая часть сигнала меняет свою амплитуду во времени, т.е. она модулируется неким более низкочастотным сигналом. Оказывается, что именно в этом модулирующем сигнале содержится и информация о состоянии подшипника. Выделение и обработка этой информации и составляют основу этого метода. Экспериментально было установлено, что наилучшие результаты этот метод даёт в том случае, если анализировать модуляцию не широкополосного сигнала, получаемого от акселерометра, а предварительно осуществить полосовую фильтрацию вибросигнала в диапазоне примерно 6-10 Кгц и анализировать модуляцию этого сигнала. Для этого отфильтрованный сигнал детектируется, т.е. выделяется модулирующий сигнал (или ещё его называют «огибающая сигнала»), который подаётся на узкополосный спектроанализатор и мы получаем спектр интересующего нас модулирующего сигнала или спектр огибающей. Что и дало название методу. Описанная последовательность обработки сигнала представлена для наглядности на рис. 7.4. 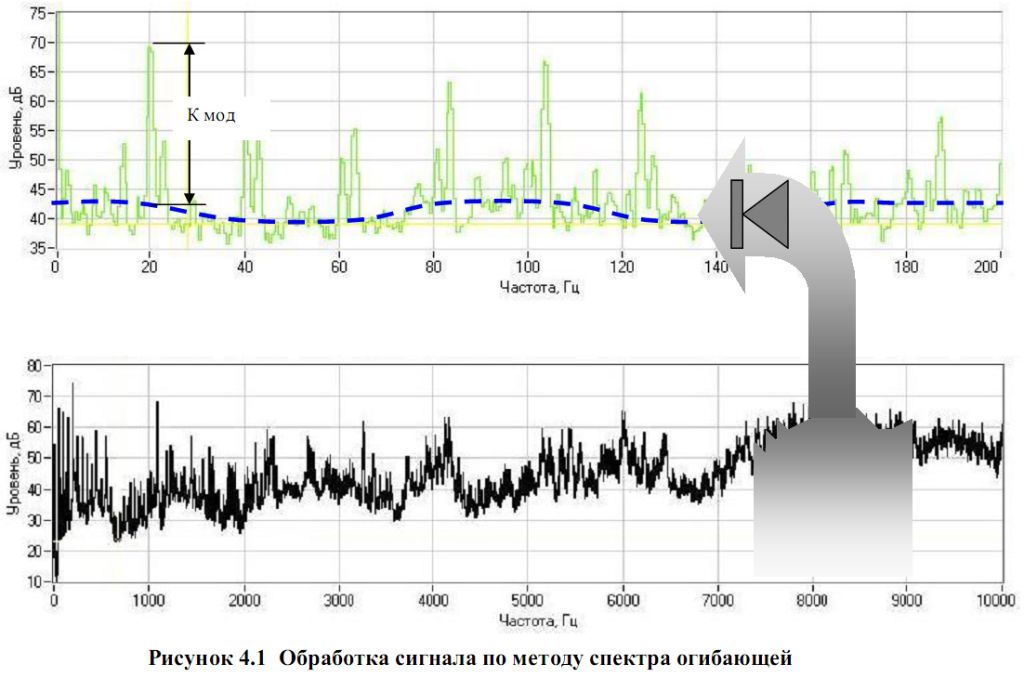 Рис. 7.4. Обработка сигнала по методу спектра огибающей Видно, что обработка сигнала достаточно сложная, но сам результат стоит того. Дело в том, что, как уже говорилось выше, небольшие дефекты подшипника не в состоянии вызвать заметные вибрации в области низких и средних частот, генерируемых подшипником. В тоже время для модуляции высокочастотных вибрационных шумов энергии возникающих ударов оказывается вполне достаточно. Т.е. метод обладает очень высокой чувствительностью. Сам спектр огибающей имеет всегда очень характерный, специфический вид. При отсутствии дефектов он представляет собой почти горизонтальную, слегка волнистую линию. При появлении дефектов, над уровнем этой достаточно гладкой линии сплошного фона начинают возвышаться дискретные составляющие, частоты которых однозначно просчитываются по кинематике и оборотам подшипника. Частотный состав спектра огибающей позволяет идентифицировать наличие дефектов, а превышение соответствующих составляющих над фоном однозначно характеризует глубину каждого дефекта. Достоинства метода – высокая чувствительность, информативность и помехозащищенность. Основной недостаток – высокая стоимость и сложность реализации. Как правило, алгоритм обработки и анализа реализуется с использованием компьютерной техники. Метод очень широко используется в среде профессионалов и в стационарных системах мониторизации технического состояния оборудования. Метод ударных импульсов Естественно, мы опять возвращаемся к рис. 7.4. Правда, на этот раз для того, чтобы сказать, что не всё, что связано с дефектами подшипника, мы можем увидеть на этом рисунке. Там показаны вибросигналы с типичного акселерометра, работающего в диапазоне от долей Гц до 10-20 кГц. Но работающий подшипник генерирует и более высокочастотные вибрационные процессы, которые и являются здесь предметом нашего рассмотрения. Соударения дефектов подшипника вызывает возникновение высокочастотных, быстро затухающих колебаний, распространяющихся от подшипника по конструкциям механизма в виде волн сжатия/растяжения, аналогично тому, как распространяется звук в воздухе. Технология обработки сигналов показана на рис. 7.5. Наблюдаемый процесс аналогичен тому, как отзывается на удары камертон. Как бы вы по нему ни ударили – он звенит на своей собственной частоте. Так и подшипниковые узлы от соударения дефектов «звенят» на своей частоте. Частота эта обычно лежит в диапазоне 28-32 кГц. И, в отличие от камертона, эти колебания очень быстро затухают, поэтому на соответствующем образом получаемых осциллограммах они выглядят практически, как импульсы, что и дало название методу – метод ударных импульсов. Амплитуды ударных импульсов однозначно связаны со скоростью соударения дефектов и глубиной дефектов. Результаты измерений очень легко отнормировать по скорости соударения, зная геометрию подшипника и его обороты. 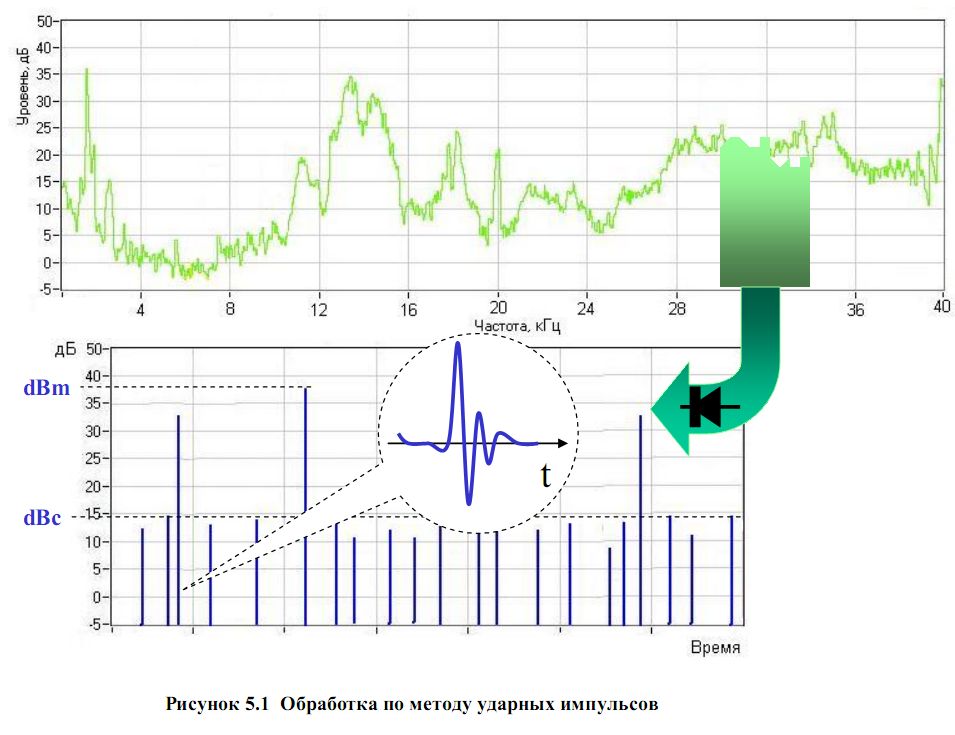 Рис. 7.5. Обработка сигнала по методу ударных импульсов Таким образом, по амплитудам ударных импульсов можно достоверно диагностировать наличие и глубину дефектов. При этом пороговые значения, характеризующие то или иное состояние подшипника, оказываются абсолютно универсальными, т.е. никак не зависят от типа и оборотов подшипника. Метод прост и дёшев в реализации, обладает высокой чувствительностью и очень широко используется как в среде профессионалов, так и эксплуатационниками оборудования, поскольку существуют простые, портативные приборы, работающие по этому методу. Для использования метода существует одно ограничение, связанное с конструктивным исполнением механизма. Поскольку речь идёт о измерении ультразвуковых волн колебаний, которые очень сильно затухают на границах разъёмных соединений, для корректных измерений необходимо, чтобы между наружным кольцом подшипника и местом установки датчика существовал сплошной массив металла. В большинстве случаев это не вызывает проблем. Сравнительные характеристики методов диагностики. В заключение раздела приведём сводную сравнительную табл. 7.1 характеристик описанных методов, где максимальная оценка параметров дана пятью звёздочками. Уточним, что это наши личные оценки, базирующиеся на собственном опыте и не претендующие абсолютную истину. Таблица 7.1 Сравнительные характеристики методов
Заключение: исследованиями установлено, что из общего количества операций ТО более 50% приходятся на контрольные работы. В то же время анализ технологических процессов ТО и ТР, магистральных локомотивов, показывает, что 30% времени используется непроизводительно. Около 20% затрачивается на локализацию дефекта, около 40% поиск дефекта, около 35% восстановление узла. Поэтому актуальна разработка широкой линейки автономных средств диагностирования с целью применения рациональных методов диагностирования оборудования локомотива. Контрольные вопросы: Сущность метода пик-фактора? Сущность метода огибающей кривой? Сущность метода ударных импульсов? | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
