Лекции по схемотехнике ЭВМ. Лекция Базовые понятия цифровой электроники версия для печати и pda в лекции рассказывается о базовых терминах цифровой электроники, о цифровых сигналах, об уровнях представления цифровых устройств, об их электрических и временных параметрах
 Скачать 5.63 Mb. Скачать 5.63 Mb.
|
Применение АЦПМикросхемы АЦП выполняют функцию, прямо противоположную функции ЦАП, — преобразуют входной аналоговый сигнал в последовательность цифровых кодов. В общем случае микросхему АЦП можно представить в виде блока, имеющего один аналоговый вход, один или два входа для подачи опорного (образцового) напряжения, а также цифровые выходы для выдачи кода, соответствующего текущему значению аналогового сигнала (рис. 13.13). Часто микросхема АЦП имеет также вход для подачи тактового сигнала CLK, сигнал разрешения работы CS и сигнал, говорящий о готовности выходного цифрового кода RDY. На микросхему подается одно или два питающих напряжения и общий провод. В целом микросхемы АЦП сложнее, чем микросхемы ЦАП, их разнообразие заметно больше, и поэтому сформулировать для них общие принципы применения сложнее. 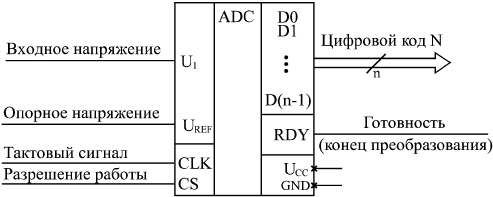 Рис. 13.13. Микросхема АЦП Опорное напряжение АЦП задает диапазон входного напряжения, в котором производится преобразование. Оно может быть постоянным или же допускать изменение в некоторых пределах. Иногда предусматривается подача на АЦП двух опорных напряжений с разными знаками, тогда АЦП способен работать как с положительными, так и с отрицательными входными напряжениями. Выходной цифровой код N (n-разрядный) однозначно соответствует уровню входного напряжения. Код может принимать 2n значений, то есть АЦП может различать 2n уровней входного напряжения. Количество разрядов выходного кода n представляет собой важнейшую характеристику АЦП. В момент готовности выходного кода выдается сигнал окончания преобразования RDY, по которому внешнее устройство может читать код N. Управляется работа АЦП тактовым сигналом CLK, который задает частоту преобразования, то есть частоту выдачи выходных кодов. Предельная тактовая частота — второй важнейший параметр АЦП. В некоторых микросхемах имеется встроенный генератор тактовых сигналов, поэтому к их выводам подключается кварцевый генератор или конденсатор, задающий частоту преобразования. Сигнал CS разрешает работу микросхемы. Выпускается множество самых разнообразных микросхем АЦП, различающихся скоростью работы (частота преобразования от сотен килогерц до сотен мегагерц), разрядностью (от 6 до 24), допустимыми диапазонами входного сигнала, величинами погрешностей, уровнями питающих напряжений, методами выдачи выходного кода (параллельный или последовательный), другими параметрами. Обычно микросхемы с большим количеством разрядов имеют невысокое быстродействие, а наиболее быстродействующие микросхемы имеют небольшое число разрядов. Область применения любой микросхемы АЦП во многом определяется использованным в ней принципом преобразования, поэтому необходимо знать особенности этих принципов. Для выбора и использования АЦП необходимо пользоваться подробными справочными данными от фирмы-производителя. 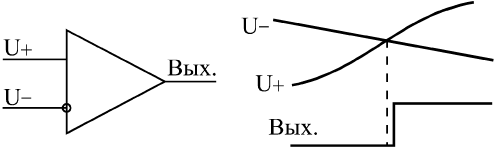 Рис. 13.14. Компаратор напряжения В качестве базового элемента любого АЦП используется компаратор напряжения (рис. 13.14), который сравнивает два входных аналоговых напряжения и, в зависимости от результата сравнения, выдает выходной цифровой сигнал — нуль или единицу. Компаратор работает с большим диапазоном входных напряжений и имеет высокое быстродействие (задержка порядка единиц наносекунд). 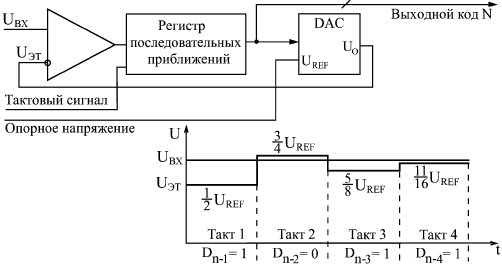 Рис. 13.15. АЦП последовательного типа Существует два основных принципа построения АЦП: последовательный и параллельный. В последовательном АЦП входное напряжение последовательно сравнивается одним единственным компаратором с несколькими эталонными уровнями напряжения, и в зависимости от результатов этого сравнения формируется выходной код. Наибольшее распространение получили АЦП на основе так называемого регистра последовательных приближений (рис. 13.15). Входное напряжение подается на вход компаратора, на другой вход которого подается эталонное напряжение, ступенчато изменяющееся во времени. Выходной сигнал компаратора подается на вход регистра последовательных приближений, тактируемого внешним тактовым сигналом. Выходной код регистра последовательных приближений поступает на ЦАП, которое из опорного напряжения формирует меняющееся эталонное напряжение. Регистр последовательных приближений работает так, что в зависимости от результата предыдущего сравнения выбирается следующий уровень эталонного напряжения по следующему алгоритму:
Понятно, что процесс этот довольно медленный, требует нескольких тактов, причем в течение каждого такта должны успеть сработать компаратор, регистр последовательных приближений и ЦАП с выходом по напряжению. Поэтому последовательные АЦП довольно медленные, имеют сравнительно большое время преобразования и малую частоту преобразования. Второй тип АЦП — АЦП параллельного типа — работает по более простому принципу. Все разряды выходного кода вычисляются в них одновременно (параллельно), поэтому они гораздо быстрее, чем последовательные АЦП. Правда, они требуют применения большого количества компараторов (2n–1), что вызывает чисто технологические трудности при большом количестве разрядов (например, при 12-разрядном АЦП требуется 4095 компараторов). Схема такого АЦП (рис. 13.16) включает в себя резистивный делитель из 2n одинаковых резисторов, который делит опорное напряжение на (2n–1) уровней. 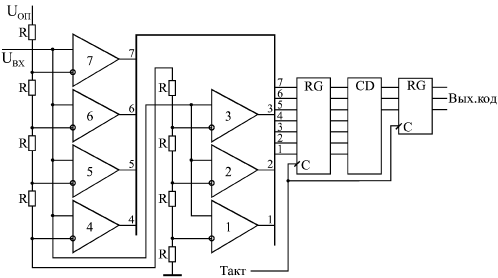 Рис. 13.16. 3-разрядный АЦП параллельного типа Входное напряжение сравнивается с помощью компараторов с уровнями, формируемыми делителем напряжения. Выходные сигналы компараторов с помощью шифратора преобразуются в n-разрядный двоичный код. Шифратор выдает на выход номер последнего из сработавших (то есть выдавших сигнал логической единицы) компараторов. Например, в случае 3-разрядного АЦП (на рисунке) при величине входного напряжения от 0 до 1/8 опорного напряжения выходной код будет 000, при входном напряжении от 1/8 до 2/8 опорного напряжения сработает первый компаратор, что даст выходной код 001, при входном напряжении от 2/8 до 3/8 опорного напряжения сработают компараторы 1 и 2, что даст выходной код 010, и т.д. Процесс преобразования происходит в параллельном АЦП очень быстро, поэтому частота преобразования может достигать сотен мегагерц. Для повышения быстродействия в параллельном АЦП иногда применяется конвейерный принцип: выходной код компараторов записывается в (2n–1)-разрядный параллельный регистр, показанный на рис. 13.16. Выходной код шифратора также записывается в n-разрядный параллельный регистр. Оба регистра в этом случае тактируются одним и тем же тактовым сигналом. Это снижает требования к быстродействию компараторов и шифратора. Правда, выходной код АЦП задерживается из-за таких регистров на два периода таковой частоты. Громоздкость структуры параллельного АЦП приводит к тому, что в некоторых АЦП применяется смешанный параллельно-последовательный принцип. Это несколько снижает быстродействие подобного АЦП по сравнению с обычным параллельным АЦП, но зато позволяет получить большое число разрядов, не увеличивая количество компараторов до (2n–1). Для того чтобы АЦП любого типа работал с использованием всех своих возможностей, необходимо обеспечить согласование диапазона изменения входного аналогового сигнала с допустимым диапазоном (динамическим диапазоном) входного напряжения АЦП. На рис. 13.17 показано четыре возможных случая соотношения динамического диапазона АЦП (от 0 до UREF или от UREF1 до UREF2) и входного сигнала. В случаях а и б входной сигнал меньше динамического диапазона, поэтому АЦП будет работать правильно, но не будет использовать всех своих возможностей. В случае в входной сигнал слишком большой, поэтому часть его значений не будет преобразована. Только в случае г АЦП действительно будет работать как n-разрядный и будет преобразовывать все значения входного сигнала. Для согласования входного сигнала с динамическим диапазоном АЦП можно применять усилители, аттенюаторы, схемы сдвига. В некоторых случаях согласование может быть достигнуто простым выбором величин опорных напряжений. 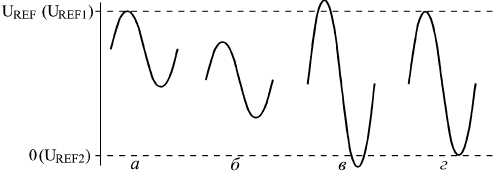 Рис. 13.17. Соотношение входного сигнала и динамического диапазона АЦП 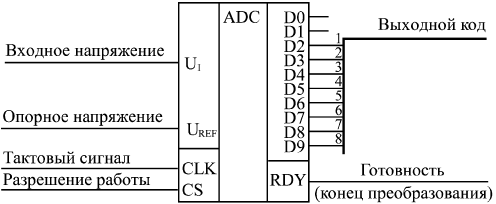 Рис. 13.18. Уменьшение количества разрядов выходного кода АЦП Иногда бывает необходимо уменьшить количество разрядов АЦП. В этом случае нужное количество младших разрядов выходного кода микросхемы просто не используется. На рис. 13.18 показано использование 10-разрядного АЦП в качестве 8-разрядного. Обратная задача — увеличение разрядности АЦП — встречается чаще. Существует ряд типичных схемотехнических решений по объединению нескольких микросхем АЦП для увеличения количества разрядов выходного кода, но большинство этих решений требует сложных расчетов результирующих погрешностей преобразования и применения аналоговых узлов. Мы не будем их здесь рассматривать. Отметим только, что при возникновении задачи увеличения разрядности надо прежде всего попытаться найти микросхему с нужным количеством разрядов, и только потом рассматривать возможности объединения нескольких микросхем АЦП. Рассмотрим несколько типичных схем включения АЦП, используемых в аналого-цифровых системах. 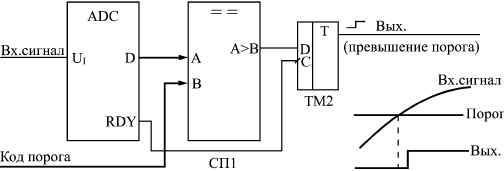 Рис. 13.19. Фиксатор превышения входным сигналом установленного порога Первая схема (рис. 13.19) предназначена для фиксации момента превышения входным аналоговым сигналом заданного порогового напряжения. Схема вырабатывает выходной сигнал (положительный фронт) тогда, когда входной аналоговый сигнал становится больше установленного уровня, причем уровень этот задается цифровым кодом порога. Код порога сравнивается с выходными кодами АЦП с помощью микросхемы компаратора кодов. Выходной сигнал компаратора кодов записывается в триггер по сигналу RDY с АЦП, что позволяет исключить влияние коротких импульсов, возникающих на выходе компаратора в момент изменения входных кодов. Применение этого триггера задерживает выходной сигнал на один такт. Может показаться, что применение АЦП в данном случае не оправданно, избыточно. Но надо учитывать, что в аналого-цифровых системах АЦП, преобразующий входной сигнал в последовательность кодов, как правило, уже есть, поэтому дополнительного АЦП не требуется, достаточно только включить компаратор кодов и триггер. АЦП также применяется в схемах вычисления амплитуды входного аналогового сигнала. Для такого вычисления можно использовать уже рассмотренную схему вычислителя экстремального значения входного кода (см. рис. 8.9). В качестве источника последовательности входных кодов в данном случае выступает АЦП (рис. 13.20). 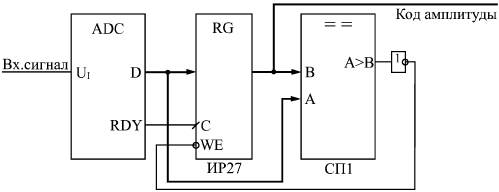 Рис. 13.20. Вычислитель амплитуды аналогового сигнала В регистр со входом разрешения записи записывается код с выхода АЦП по сигналу RDY в том случае, если текущее значение кода больше значения кода, записанного ранее в регистр. В результате уже после одного периода входного сигнала в регистре будет код амплитуды входного сигнала. За период преобразования АЦП должны успеть сработать компаратор кодов и регистр. Если такой вычислитель амплитуды входного сигнала используется в составе сложной аналого-цифровой системы, в которой уже присутствует АЦП, непрерывно преобразующий входной сигнал в коды, то дополнительно требуются только цифровые микросхемы: компаратор кодов и регистр. 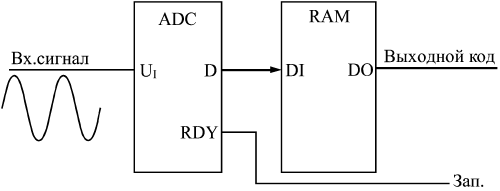 Рис. 13.21. Включение буферной памяти для запоминания кодов с выходов АЦП Наиболее часто встречающееся использование АЦП — это преобразование входного сигнала в поток кодов, причем коды эти обычно записываются в буферную память. В данном случае наиболее подходящим является однонаправленный буфер с периодическим режимом работы. То есть сначала в буферную память заносится массив кодов выборок входного сигнала, а затем этот массив читается для дальнейшей обработки. Именно так, например, строится цифровой осциллограф, предназначенный для наблюдения аналоговых сигналов на экране. Схема включения АЦП в этом случае показана на рис. 13.21. В качестве строба записи в буферную память используется сигнал RDY с АЦП. Подробнее организацию буфера мы уже рассматривали в предыдущей лекции. Конечно, в реальных аналого-цифровых устройствах все гораздо сложнее, в них требуются схемы синхронизации процесса записи со входным сигналом, схемы предварительной обработки аналогового сигнала, но суть остается той же — буферная память, записывающая последовательность кодов с выхода АЦП. Чем больше объем памяти, тем больший фрагмент входного аналогового сигнала она может запомнить. Например, если память имеет организацию 64Кх8 и работает с 8-разрядным АЦП, то при частоте преобразования АЦП 10 МГц буфер сможет хранить в себе фрагмент аналогового сигнала длительностью 6,5536 мс. Наконец, последняя схема, которую мы рассмотрим (рис. 13.22), позволяет вдвое повысить быстродействие АЦП, точнее, поднять вдвое частоту записи кодов выборок входного сигнала в буферную память. 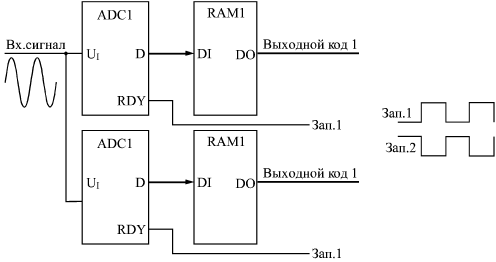 Рис. 13.22. Увеличение вдвое частоты преобразования входного сигнала с помощью двух АЦПс буферами Идея схемы очень проста: используется два АЦП и два буфера, которые работают по очереди, например, четные выборки входного сигнала обрабатывает один АЦП со своим буфером, а нечетные — другой АЦП со своим буфером. В результате запоминание кодов входного сигнала осуществляется с частотой вдвое больше частоты преобразования каждого из АЦП. Например, если каждый АЦП и каждый буфер работают с частотой 10 МГц, то результирующая частота преобразования составит 20 МГц. Тактовые сигналы АЦП и сигналы RDY на выходах АЦП должны быть сдвинуты один относительно другого на половину периода тактового сигнала. Чтение зарегистрированных кодов из обоих буферов также должно быть организовано по очереди: первый код читается из первого буфера, второй — из второго, третий — опять из первого, четвертый — из второго и т.д. Объем обоих буферов в данном случае складывается. Например, при организации каждого буфера 64Кх8 результирующий буфер будет иметь организацию 128Кх8. Пользуясь этим же принципом, можно повысить частоту обработки входного сигнала с помощью АЦП не только вдвое, но и втрое, в четыре раза и т.д. Необходимо только согласовать во времени работу соответственно трех, четырех и т.д. АЦП, у каждого из которых должна быть своя буферная память. Помимо упомянутых здесь АЦП последовательно и параллельного типов существуют еще и АЦП с промежуточным преобразованием. В них входной аналоговый сигнал с помощью аналогового интегратора преобразуется во временной интервал между цифровыми импульсами или в частоту следования цифровых импульсов. Выходной цифровой код, соответствующий входному аналоговому сигналу формируется в результате измерения длительности временного интервала или частоты следования импульсов (рис. 13.23). Если используется выходная частота, то такой АЦП называется "преобразователем напряжение—частота" (ПНЧ). Такой подход позволяет с помощью сравнительно простых аппаратных средств получить высокую точность преобразования, не зависящую от многих параметров используемых компонентов и от характеристик окружающей среды. Измерение временных интервалов и частоты следования импульсов осуществляется простейшими цифровыми схемами, примеры которых приведены в лекциях 9, 10. Измерения эти могут осуществляться с высокой точностью вследствие того, что существует очень хороший временной эталон — кварцевый генератор. Отметим, что достоинством ПНЧ является также возможность простой передачи его выходного цифрового сигнала на большие расстояния. 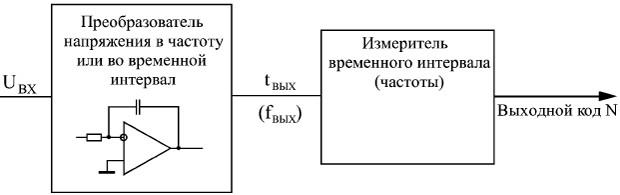 Рис. 13.23. АЦП с промежуточным преобразованием В конце лекции надо еще раз отметить, что приведенные здесь схемы сильно упрощены. Для их практической реализации необходимо знание не только цифровой схемотехники, но и аналоговой и аналого-цифровой схемотехники, а также знание особенностей конкретных микросхем ЦАП и АЦП, что не является предметом данной книги. Однако рассмотренные ключевые принципы использования ЦАП и АЦП и их совместного включения с цифровыми схемами будут полезны любому разработчику. | ||||||||||||||||||||
| | ||||||||||||||||||||
| 14. Лекция: Разработка простых цифровых устройств: версия для печати и PDA В лекции подробно рассматриваются примеры разработки простых цифровых устройств — клавиатуры и вычислителя контрольной суммы, начиная от анализа функций устройств и выделения основных узлов до проектирования принципиальных схем узлов и устройства в целом. | ||||||||||||||||||||
| | ||||||||||||||||||||
| | ||||||||||||||||||||
| | ||||||||||||||||||||
| В предыдущих лекциях были рассмотрены базовые элементы цифровой схемотехники и простейшие приемы проектирования узлов на их основе. Но для разработки сложных устройств и систем всех этих знаний порой оказывается недостаточно. Чтобы создать сложное устройство, необходимо еще владеть приемами системотехники, то есть уметь на основании анализа функций, которые должно выполнять устройство в целом, спроектировать его структуру, сформулировать принципы взаимодействия узлов, четко определить все задачи, которые должен решать каждый из узлов, выработать требования к отдельным узлам. Возможно, в результате всех этих шагов будет изменена сама первоначальная задача, будут переформулированы требования к создаваемому устройству, к его месту в системе, к принципам его взаимодействия с другими устройствами. И только потом, после всей этой предварительной работы уже можно переходить к разработке узлов, собственно к схемотехнике. Приемы системотехники сформулировать, формализовать, описать, даже перечислить гораздо сложнее, чем приемы схемотехники. Да и пользы от такой формализации зачастую немного. Проектирование сложного, надежно работающего цифрового устройства с минимальными аппаратными затратами сродни искусству и требует от разработчика определенных способностей, даже таланта. Научить этому практически невозможно. Более того, попытка научить системотехнике может даже принести вред, так как ограничит творческие способности разработчика несколькими жесткими стандартными алгоритмами. Однако можно показать несколько простейших примеров разработки, продемонстрировать последовательность шагов, которые необходимы при проектировании, которые могут встретиться в процессе создания устройств некоторых распространенных типов. Исходя из этих примеров, разработчик может в дальнейшем попробовать по аналогии создать что-то свое, более или менее совершенное, но обязательно работоспособное. Поэтому в данной лекции как раз и будут подробно рассмотрены несколько простых примеров проектирования сравнительно сложных устройств на всех этапах: от анализа решаемой задачи до создания полной принципиальной схемы. Примеры эти, конечно, не отражают и малой доли всех реально встречающихся задач, но относятся к различным классам цифровых устройств. Разработка клавиатурыРазличные клавиатуры с большим количеством клавиш (кнопок) широко используются в цифровых системах: в компьютерах, контроллерах, измерительных приборах, в бытовой технике. Основная задача любой клавиатуры довольно проста: она должна при любом нажатии на клавишу выдавать код номера этой клавиши и сигнал флага нажатия клавиши (строб этого кода). Получив этот сигнал флага, внешнее устройство читает код нажатой клавиши и предпринимает требуемые действия. Главная задача при проектировании клавиатуры состоит в минимизации аппаратных затрат и в обеспечении надежного срабатывания в любой ситуации. Существует масса схемотехнических решений этой задачи — от примитивных до сложнейших. Клавиатуры могут быть механическими, квазисенсорными или сенсорными, клавиатуры могут иметь жесткую логику работы или быть интеллектуальными, даже допускать перепрограммирование. Мы будем в качестве примера рассматривать самую простую механическую клавиатуру с жесткой логикой работы. Количество клавиш полноразмерной клавиатуры компьютера превышает сотню, поэтому мы будем проектировать клавиатуру на максимальное количество клавиш, равное 128. Естественно, клавиатура должна иметь защиту от дребезга механических контактов и должна корректно обрабатывать ситуацию одновременного нажатия нескольких клавиш. Примем, например, что при одновременном нажатии нескольких клавиш клавиатура должна выдавать код только одной из них. Примем также, что максимально возможный темп нажатия клавиш на клавиатуре не должен превышать 20 нажатий в секунду (это довольно много). Таким образом, основные требования к проектируемому устройству сформулированы. Начнем разработку. Очень часто удобным и эффективным приемом является начало разработки устройства "с конца". То есть проектирование начинается исходя из требуемого результата, из тех сигналов, которые устройство должно выдавать вовне и принимать извне. И только в конце проектирования разрабатывается та часть устройства, которая выполняет требуемую функцию. Такой подход гарантирует, что разработанное устройство не будет чрезмерно избыточным, не будет делать ничего лишнего, а также то, что оно корректно будет взаимодействовать с другими устройствами и системами. Этот принцип проектирования не универсален, порой выдержать его в течение всего процесса разработки трудно, но попробовать его применить к любому устройству никогда не помешает. В нашем случае необходимо сначала определиться, что должна выдавать вовне клавиатура. Обычно это задается техническим заданием, но мы примем, что наша клавиатура должна выдавать 7-разрядный двоичный номер нажатой клавиши (так как 27 = 128) и сопровождать его положительным сигналом флага нажатия. Сигнал флага и код клавиши должны сохраняться до тех пор, пока нажата клавиша. За это время (несколько миллисекунд) внешнее устройство должно успеть проанализировать сигнал флага и прочитать выходной код клавиатуры. Обычно данное требование не слишком жесткое. Альтернативное решение — сохранение кода нажатой клавиши и сигнала флага до момента чтения выходного кода внешним устройством — конечно же, снижает требование к быстродействию читающего внешнего устройства, однако оно может привести к тому, что некоторые нажатия клавиш останутся без реакции, не будут обработаны. Также необходимо определиться, как клавиатура будет вести себя при одновременном нажатии нескольких клавиш. Наиболее сложные, интеллектуальные клавиатуры выдают последовательно коды всех нажатых клавиш, запоминая их в буферной памяти. Но мы примем, что клавиатура должна выдавать только код одной из одновременно нажатых клавиш (первой по установленному порядку). Нажатия всех остальных клавиш одновременно с данной просто игнорируются. При проектировании механической клавиатуры важно решить, как будет обрабатываться неизбежно присутствующий дребезг механических контактов клавиш. Его можно обрабатывать как внутри клавиатуры, так и вне ее (то есть перенести эту функцию на внешнее устройство). Оба эти подхода имеют свои преимущества. Но наша клавиатура будет обрабатывать дребезг контактов самостоятельно. Принцип обработки выбираем очень простой: первое зафиксированное замыкание контактов клавиши считается началом нажатия, а конец нажатия определяется тогда, когда контакты будут разомкнуты в течение заданного интервала времени. В результате временная диаграмма работы разрабатываемой клавиатуры может быть упрощенно представлена в виде рис. 14.1. Здесь сигнал флага начинается при фиксации единичного сигнала с клавиши (это может быть как во время дребезга, так и после его окончания). После выставления флага фиксируется выходной код клавиши. После отпускания клавиши (нулевой сигнал), через время задержки tзад снимается сигнал флага. Время задержки должно быть заведомо больше времени дребезга контактов. Выходной код может сохраняться после отпускания клавиши до следующего нажатия, а может и сниматься. 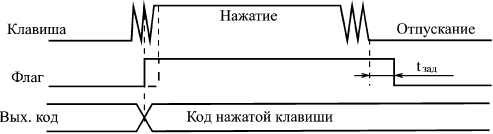 Рис. 14.1. Временная диаграмма работы клавиатуры Дальнейшая разработка невозможна без выбора принципа преобразования сигналов от нажатия клавиш в код номера нажатой клавиши. Простейшим путем построения подобного преобразователя является использование приоритетных шифраторов (рис. 14.2). Каждая клавиша дает свой логический сигнал, сигналы от всех клавиш преобразуются шифратором в код номера клавиши. Однако такой простейший подход хорош только при небольшом количестве клавиш (до 8 или до 16), так как при большом количестве входов приоритетный шифратор получается довольно сложным. При малом количестве клавиш дребезг контактов обычно устраняется отдельно для каждой клавиши с помощью RS-триггера (как это показано на рисунке). Это решение простое, но требующее больших аппаратурных затрат. 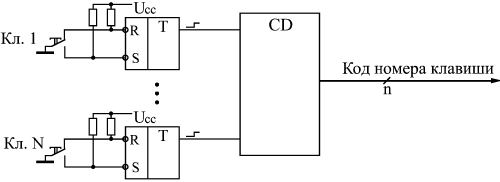 Рис. 14.2. Простейший преобразователь для клавиатуры Другим путем построения преобразователя является использование так называемой коммутационной матрицы, состояние которой периодически опрашивается с частотой тактового генератора. Коммутационная матрица представляет собой две группы пересекающихся проводников (строки и столбцы), во всех точках пересечения которых находятся клавиши. В данном случае каждая клавиша не формирует своего отдельного логического сигнала, а только коммутирует (соединяет) одну из строк матрицы с одним из ее столбцов. Наиболее универсальная схема преобразователя, легко наращиваемая и достаточно простая, приведена на рис. 14.3. Для опроса коммутационной матрицы применяется счетчик, тактируемый генератором. Старшие разряды счетчика используются для выбора одной из строк матрицы с помощью дешифратора (на выбранную строку поступает сигнал логического нуля, на невыбранную — сигнал логической единицы). Младшие разряды счетчика используются для опроса столбцов матрицы с помощью мультиплексора. Сигнал с опрашиваемого столбца подается на выход мультиплексора. Признаком нажатия клавиши является нулевой сигнал на выходе мультиплексора. В этот момент на выходах счетчика присутствует код номера нажатой клавиши. Такая схема легко позволяет строить клавиатуры на большое количество клавиш (до 256, как на рисунке, и даже больше), однако она требует довольно большого времени для полного опроса клавиатуры (так как количество тактов опроса равно полному количеству клавиш). 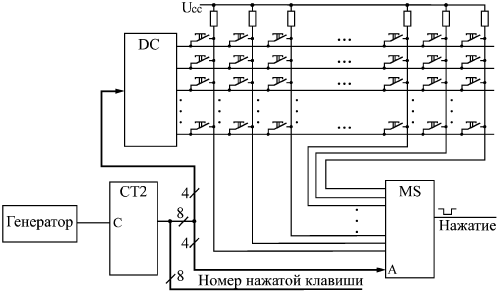 Рис. 14.3. Преобразователь с опросом всех клавиш Совмещение двух рассмотренных подходов позволяет создавать достаточно большие клавиатуры с малыми аппаратурными затратами и малым временем опроса. При таком комбинированном методе (рис. 14.4) также используется коммутационная матрица с клавишами на всех пересечениях строк и столбцов, но опрашиваются не все клавиши по очереди, а только строки (или столбцы) матрицы. Для опроса, как и в предыдущем случае, применяются генератор, счетчик и дешифратор. Положение же нажатой клавиши в строке (или в столбце) определяется с помощью шифратора. Код нажатой клавиши образуется из выходного кода счетчика (старшие разряды) и кода с выхода шифратора (младшие разряды). В нашем случае клавиатура имеет 128 клавиш, то есть коммутационная матрица должна состоять из 16 строк, опрашиваемых дешифратором 4–16 (ИД3), и 8 столбцов, сигналы с которых обрабатываются шифратором 8–3 (ИВ1). Счетчик должен иметь 4 разряда (ИЕ7). Эти 4 разряда и 3 разряда с выхода шифратора дадут 7-разрядный номер нажатой клавиши. Полный цикл опроса клавиатуры будет занимать 16 тактов генератора (по числу строк). Признаком нажатия одной из клавиш будет отрицательный сигнал на выходе –GS шифратора. Если нажато несколько клавиш в разных строках, то обрабатываться будет та клавиша, строка которой будет опрошена первой. Если нажато несколько клавиш в одной строке, то шифратор выдаст код клавиши, соответствующей большему номеру входа. Надо также учитывать, что шифратор ИВ1 выдает инверсный номер входа, на который пришел нулевой сигнал, — эта особенность может потребовать применения трех выходных инверторов (на рисунке не показаны). 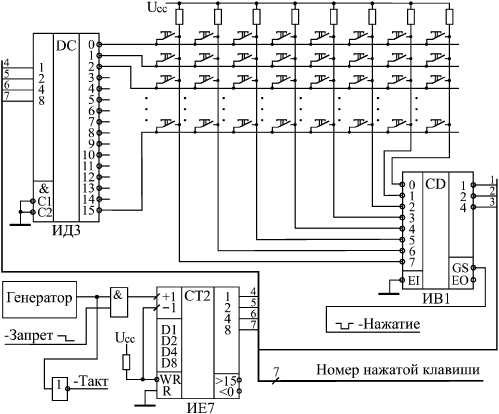 Рис. 14.4. Преобразователь с опросом строк клавиш Оценим, какой должна быть частота тактового генератора. Мы приняли, что максимальная скорость нажатия равна 20 раз в секунду. Значит, за 1/20 секунды надо успеть опросить всю клавиатуру, то есть все 16 строк. Таким образом, минимально допустимая тактовая частота составляет 16•20 = 320 Гц. Но надо заложить и запас на обработку дребезга контактов. Поэтому примем тактовую частоту опроса равной 400 Гц. Она может быть и больше, но чрезмерно увеличивать ее (например, выше 1 кГц) не стоит, так как при быстром переключении микросхем увеличивается потребляемый схемой ток. Понятно, что генератор должен быть не кварцевым, так как кварцевые резонаторы на низкие частоты не выпускаются, а делитель частоты резко усложнит схему. К тому же точная выдержка частоты генератора в данном случае совершенно не нужна. Выходной сигнал "–Нажатие", конечно же, будет иметь короткие паразитные импульсы. Во-первых, они будут возникать из-за дребезга контактов нажатой в данный момент клавиши. Во-вторых, они могут появляться из-за переходных процессов при переключении счетчика и дешифратора. Эти паразитные импульсы надо исключать. Чтобы исключить действие паразитных импульсов из-за переходных процессов при переключении счетчика и дешифратора достаточно применить стробирование или тактирование сигнала "–Нажатие" в середине каждого тактового интервала. Для этого из схемы преобразователя надо вывести сигнал "–Такт". Исключение коротких выходных импульсов из-за дребезга контактов клавиш сложнее. Прежде всего, на время нажатия клавиши целесообразно остановить опрос строк с помощью сигнала "–Запрет". Затем надо обработать сигнал "?Нажатие" по принципу, показанному на рис. 14.1. Будем считать, что при дребезге контактов длительность кратковременного размыкания не превышает периода тактового генератора (2,5 мс при тактовой частоте 400 Гц). Тогда задержка окончания сигнала флага нажатия (см. рис. 14.1) должна быть не менее одного периода тактового сигнала. Для выработки задержки можно использовать цепочку триггеров, тактируемых сигналом "–Такт". Схема выработки выходных сигналов клавиатуры приведена на рис. 14.5. 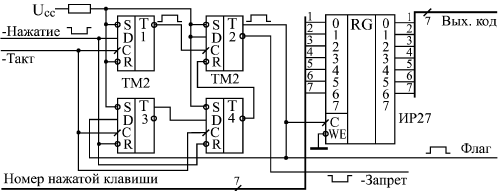 Рис. 14.5. Схема выработки выходных сигналов клавиатуры Триггер Т1 перебрасывается в единицу (на инверсном выходе) тогда, когда в середине тактового интервала (по положительному фронту сигнала "–Такт") сигнал "–Нажатие" нулевой. Своим выходным сигналом триггер Т1 перебрасывает в единицу триггер Т2, который уже никак не связан с сигналом "–Нажатие", не реагирует ни на какой дребезг этого сигнала. Выходной сигнал триггера Т2 используется в качестве сигнала флага нажатия клавиатуры. Инверсный сигнал с выхода триггера Т2 используется в качестве сигнала "–Запрет", останавливающего опрос строк клавиатуры. Цепочка триггеров Т3 и Т4, тактируемая сигналом "Такт", служит для задержки снятия сигнала флага после отпускания клавиши (когда сигнал "–Нажатие" становится равным единице). После установки флага в единицу, сигнал флага начинает записываться по фронту сигнала "–Такт" в триггеры Т3 и Т4, но только в том случае, когда сигнал "–Нажатие" установлен в единицу. В результате на инверсном выходе триггера Т4 появится сигнал логического нуля при нахождении сигнала "–Нажатие" в единице в моменты двух последовательных положительных фронтов сигнала "–Такт". Сигнал с выхода Т4 сбрасывает сигнал флага в нуль, после чего вся схема переходит в исходное состояние и ждет следующего нулевого сигнала "–Нажатие". Если кратковременное размыкание при дребезге контактов клавиш длится более 2,5 мс, то можно увеличить количество триггеров в последовательной цепочке (Т3 и Т4), что приведет к увеличению задержки снятия сигнала флага на целое число тактов генератора. Таким образом, схема полностью разработана. Отметим, что низкая тактовая частота работы схемы позволяет нам не рассчитывать задержек микросхем, то есть использовать только первый уровень представления, логическую модель. А эффекты, связанные с переходными процессами при переключении микросхем, мы устранили, обеспечив временной сдвиг на половину периода генератора между тактовыми сигналами схемы преобразователя (рис. 14.4) и схемы выработки выходных сигналов (рис. 14.5). Все резисторы, примененные в схеме, должны быть номиналом около 1 кОм. Разработка вычислителя контрольной суммыРазличные контрольные суммы широко применяются в цифровых устройствах и системах для контроля правильности хранения или передачи массивов информации. Суть этого метода контроля проста: к хранимому или передаваемому информационному массиву присоединяется небольшой контрольный код (обычно от 1 разряда до 32 разрядов), в котором в свернутом виде содержится информация обо всем массиве. При чтении или получении этого массива еще раз вычисляется тот же самый контрольный код по тому же самому алгоритму. Если этот вновь вычисленный код равен тому коду, который был присоединен к массиву, то считается, что массив сохранен или передан без ошибок. Логика здесь следующая: контрольный код (он же контрольная сумма) гораздо меньше контролируемого массива, поэтому вероятность искажения контрольной суммы гораздо меньше, чем вероятность искажения массива. Если же исказятся как массив, так и контрольная сумма, то вероятность того, что эти искажения не будут замечены при повторном подсчете контрольной суммы, крайне мала. Существует, правда, вероятность, что массив будет искажен в нескольких местах таким образом, что контрольная сумма от этих искажений никак не изменится, но такая вероятность также обычно мала. Контрольные суммы применяются при хранении данных в памяти (оперативной и постоянной), при хранении данных на магнитных носителях (дисках, лентах), в локальных и глобальных сетях передачи информации. В случае защиты контрольной суммой хранимой информации можно определить, что данный массив (файл, сектор на диске) испорчен и его нельзя использовать. В случае защиты контрольной суммой передаваемой по сети информации приемник может потребовать от передатчика повторной передачи искаженного массива. Существует множество способов вычисления контрольной суммы, различающихся степенью сложности вычисления и надежностью выявления ошибок. Но наибольшее распространение получил в настоящее время так называемый "циклический метод контроля по избыточности" или CRC (Cyclic Redundancy Check), при котором применяется циклическая контрольная сумма. Вычисляется циклическая контрольная сумма следующим образом. Весь массив информации рассматривается как одно N-разрядное двоичное число, где N — количество бит во всех байтах массива. Для вычисления контрольной суммы это N-разрядное число делится на некоторое постоянное число (полином), выбранное специальным образом (но делится не просто, а по модулю 2). Частное от этого деления отбрасывается, а остаток как раз и используется в качестве контрольной суммы. Мы не будем углубляться в математическое обоснование этого метода. Интересующиеся читатели могут обратиться к специальной литературе. Здесь же мы отметим только, что данный метод выявляет одиночные ошибки в массиве с вероятностью 100%, а любое другое количество ошибок с вероятностью, примерно равной 1–2-n, где n — количество разрядов контрольной суммы (это верно только при условии, что N гораздо больше n, что, впрочем, почти всегда выполняется). Например, при n = 8 данная вероятность составит 0,996, для n = 16 она будет равна 0,999985, а для n = 32 она будет 0,9999999997672. Иначе говоря, почти все ошибки будут выявляться. А теперь кратко поясним, что такое деление по модулю 2. Пусть массив (последовательность бит) имеет следующий вид: 101111001110 (для простоты берем небольшую разрядность). Число, на которое делим (называемое обычно образующим полиномом) возьмем 10011. Как оно выбирается? Оно должно делиться по модулю 2 без остатка только на единицу и само на себя (то есть это должно быть простое число в смысле деления по модулю 2). Разрядность полинома берется на единицу большая, чем требуемая разрядность контрольной суммы (остатка от деления). Так, чтобы получить 8-разрядный остаток (8-разрядную контрольную сумму), надо брать 9-разрядный полином. В нашем случае полином 5-разрядный, следовательно, остаток будет 4-разрядный. Для получения 8-разрядного остатка можно использовать, например, полином 1 0001 1101 или 11D в 16-ричном коде. Деление по модулю 2 производится точно так же, как и привычное для нас деление "в столбик" (рис. 14.6), но вместо вычитания в данном случае используется поразрядное сложение по модулю 2, то есть каждый результирующий бит представляет собой функцию Исключающее ИЛИ от соответствующих битов слагаемых. Частное от деления нас не интересует, а остаток, равный в нашем примере 1000, и будет циклической контрольной суммой. 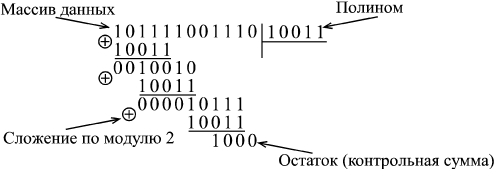 Рис. 14.6. Вычисление циклической контрольной суммы Как практически реализовать вычисление этого остатка (контрольной суммы)? Можно сделать это по приведенному здесь принципу деления в столбик (аппаратно или программно). Но в любом случае это довольно громоздко и медленно. Ускорить процесс вычисления можно, воспользовавшись табличным методом. Для этого составляется таблица чисел размером 2nхn, где n — разрядность контрольной суммы. Принцип вычисления чисел в таблице очень прост (табл. 14.1).
Числа представляют собой остаток от деления по модулю 2 числа с n конечными нулями (в нашем примере n = 8) и с n начальными разрядами, равными номеру числа (его адресу) в таблице. Деление производится на выбранный полином (в нашем случае — 9-разрядный). Таблица вычисляется один раз и хранится на диске или в ПЗУ. Алгоритм вычисления контрольной суммы с помощью этой таблицы следующий (рассматриваем случай n = 8). Берем первый байт нашего информационного массива. Рассматриваем его как адрес в таблице (номер числа). Берем из таблицы число с полученным номером — получаем остаток О1. Берем второй байт массива и складываем его по модулю 2 с остатком О1. Полученное число используем как адрес в таблице. По этому адресу выбираем из таблицы остаток О2. Берем третий байт массива, складываем его по модулю 2 с остатком О2. Используя это число как адрес в таблице, выбираем из нее остаток О3 и так продолжаем до последнего байта массива. Естественно, это будет гораздо быстрее, чем вычисление "в столбик". Реализация этого алгоритма с помощью цифровых схем требует только ПЗУ с организацией 2nхn (256х8 при 8-разрядной контрольной сумме), n-разрядного регистра и n элементов Исключающее ИЛИ (рис. 14.7). В ПЗУ заносится таблица промежуточных остатков (табл. 14.1), на вход схемы подаются один за другим байты массива, сопровождаемые стробом. Адресом ПЗУ служит сумма по модулю 2 входных данных и содержимого выходного регистра, в который по сигналу строба записывается выходной код ПЗУ. Перед началом вычисления состояние регистра обнуляется. После окончания всего массива в регистре образуется циклическая контрольная сумма. Недостаток данной схемы параллельного вычислителя очевиден: в случае большого числа разрядов контрольной суммы требуется очень большой объем ПЗУ (64Кх16 для 16-разрядной суммы и 4Гх32 для 32-разрядной суммы). Поэтому она применяется сравнительно редко. Зато параллельный вычислитель обладает высоким быстродействием (байты могут поступать с периодом, равным сумме задержки выходного регистра, времени выборки адреса ПЗУ и задержки элемента Исключающее ИЛИ). 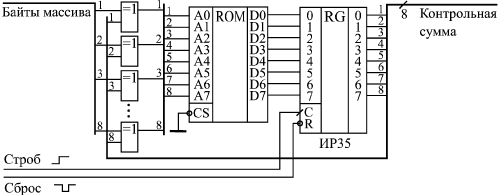 Рис. 14.7. Параллельный вычислитель 8-разрядной циклической контрольной суммы на ПЗУ Для многоразрядной контрольной суммы чаще применяется другой подход — вычисление в последовательном коде, при котором массив данных поступает на вычислитель последовательно, бит за битом. Последовательный вычислитель контрольной суммы представляет собой сдвиговый регистр с обратными связями от некоторых разрядов через сумматоры по модулю 2 (то есть элементы Исключающее ИЛИ). Полное количество разрядов регистра сдвига должно быть равно разрядности вычисляемой контрольной суммы (или, что то же самое, быть на единицу меньше разрядности используемого полинома). Место включения обратных связей однозначно определяется выбранным полиномом. Это очень похоже на генератор квазислучайной последовательности. Количество точек включения обратной связи определяется количеством единиц в полиноме (единица в младшем разряде не учитывается), а номера разрядов сдвигового регистра, с которых берутся сигналы обратной связи, определяются номерами единичных разрядов в коде полинома. В отличие от генератора квазислучайного сигнала, в данном случае необходимо смешать по функции Исключающее ИЛИ не только сигналы обратной связи, но и входной сигнал данных в последовательном коде. 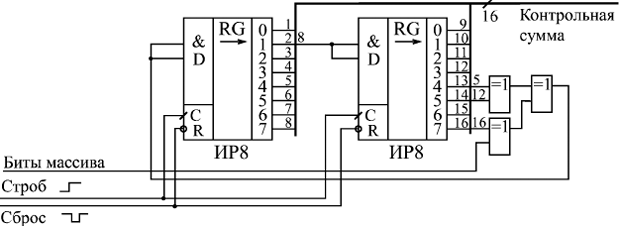 Рис. 14.8. Последовательный вычислитель 16-разрядной циклической контрольной суммы на регистре сдвига На рис. 14.8 приведен пример последовательного вычислителя 16-разрядной циклической контрольной суммы при выбранном полиноме 1 0001 0000 0010 0001 или 11021 в 16-ричном коде (рекомендация МККТТ V.41). Так как в коде полинома три единицы (без младшего разряда), необходимо взять три точки включения обратной связи. При этом номера разрядов сдвигового регистра, к которым подключаются обратные связи, определяются положением единичных битов в полиноме. Перед началом работы сдвиговый регистр необходимо сбросить в нуль (сигнал "–Сброс"). Биты массива должны сопровождаться сигналом строба. После окончания массива в регистре будет циклическая контрольная сумма. Может показаться, что такой последовательный вычислитель не слишком удобен из-за того, что данные массива должны подаваться на него в последовательном коде. Однако именно в последовательном коде передаются данные в информационных сетях, и в последовательном коде записываются данные на магнитные носители. Поэтому во всех подобных случаях последовательные вычислители идеально подходят. Период поступления битов массива на последовательный вычислитель не должен быть меньше суммы задержки регистра сдвига и элементов Исключающее ИЛИ. В итоге предельная скорость вычисления циклической контрольной суммы оказывается значительно меньшей, чем в случае параллельного вычислителя. Это также недостаток данного метода вычисления. | ||||||||||||||||||||
