Лекция 1(С.Т.О.). Лекция До сих пор мы предполагали, что источники, приемники и другие тела, относительно которых рассматривается распространение света
 Скачать 0.67 Mb.
|
|
§4 Преобразования Лоренца. Теперь решим фундаментальный вопрос о формулах преобразования координат и времени, то есть имеются в виду формулы, связывающие координаты и моменты времени одного и того же события в разных инерциальных системах отсчета (ИСО). Рассмотрим две инерциальные системы отсчета К и К’. Пусть К’ - система движется относительно К - системы со скоростью 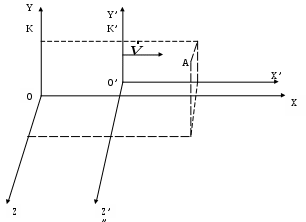 . Установим в разных точках обеих систем отсчета одинаковые часы и синхронизируем их - отдельно часы К - системы. И наконец возьмем за начало отсчета времени в обеих системах момент, когда начала координат О и О’ совпадают ( ). Постановка задачи: Предположим теперь, что в момент времени t (в К системе) в точке с координатами {x,y,z} произошло некоторое событие А - например, вспыхнула лампочка. Наша задача - найти координаты {x’,y’,z’} и момент времени t’ этого события в К’ системе. Эти формулы называются преобразованиями Лоренца - по ним осуществляется преобразование координат и времени любого события при переходе от одной инерциальной системы отсчета к другой. Преобразования Лоренца при переходе от К - к К’ - системе имеет вид: 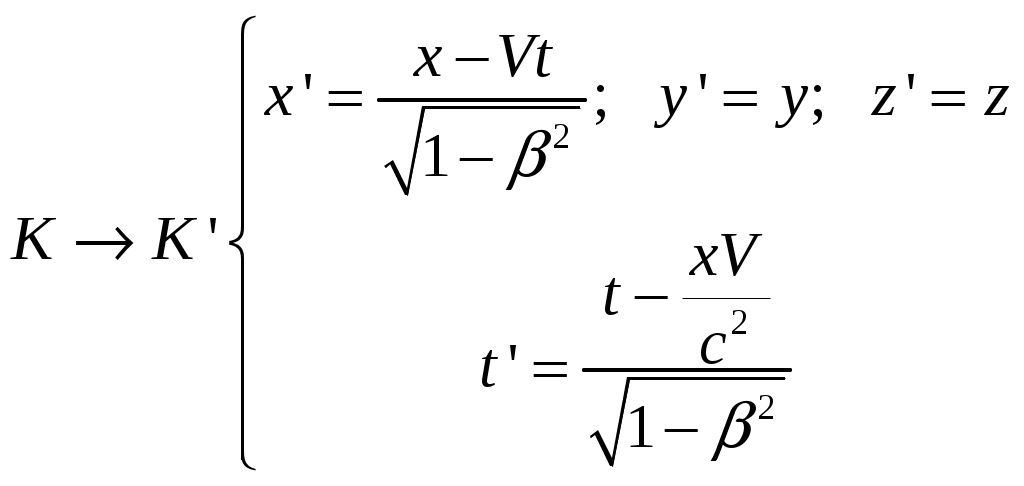 (1)При обратном переходе от К’ - к К - системе эти преобразования запишутся (ЗАМЕНИТЬ – на +): 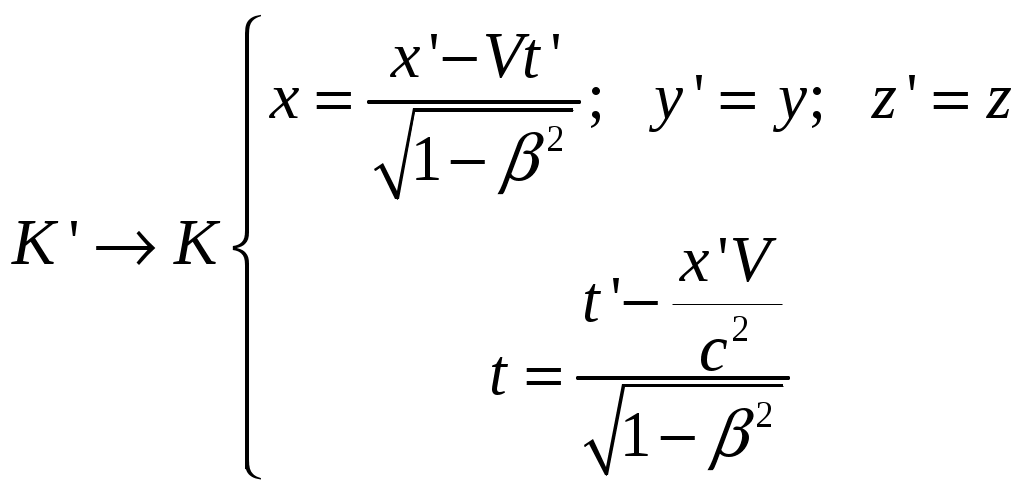 (2)где  , где V - скорость К’ - системы относительно К - системы;  м/с - скорость света в вакууме.Анализ этих формул: 1) Формулы (1) и (2) симметричны, то есть имеют одинаковый вид. Это является следствием полного равноправия обеих систем отсчета - различный знак V в этих формулах обусловлен лишь противоположным направлением движения системы К и К’ относительно друг друга. Действительно, если система К’ движется относительно К со скоростью , то в то же время система К движется относительно системы К’ со скорость (- ).2) Преобразование Лоренца при  переходит в преобразование Галилея. Таким образом, в предельном случае законы преобразования теории относительности и ньютоновской механики совпадают. Это означает, что теория относительности не отвергает преобразований Галилея как неправильные, но включает их в истинные законы преобразования как частный случай, справедливый при .3) Из преобразовании Лоренца видно, что при  подкоренные выражения становятся отрицательными и формулы теряют фактический смысл. Это соответствует тому факту, что движение тел со скоростью большей скорости света в вакууме, невозможно!Нельзя даже пользоваться системой отсчета движущейся со скоростью  . Так как при знаменатели формул для {x’и t’} и {x и t} обращается в нуль, и формулы также теряют физический смысл.Это значит, что, например, с фотоном, движущимся со скоростью c, принципиально может быть связана система отсчета. Или иначе: не существует таких систем отсчета, в которой фотон был бы неподвижным! 4) В преобразованиях Лоренца «перемешаны» координаты и время. Например, время t в К - системе определяется не только временем t’ в К’ - системе, но так же и координатой x’, то есть в формулы преобразования времени входит пространственная координата. Это важное обстоятельство указывает на неразрывную связь между пространством и временем. Другими словами, речь должна идти не отдельно о пространстве и времени, а о едином пространстве - времени, в котором протекают все физические явления. §5 Следствия из преобразований Лоренца. 1. Одновременность событий в разных системах отсчета. Пусть в системе К в точках с координатами  и  происходит одновременно два события в момент времени  .По формулам Лоренца в К’ - системе этими событиями будут соответствовать: а) координаты  ;  б) и момент времени 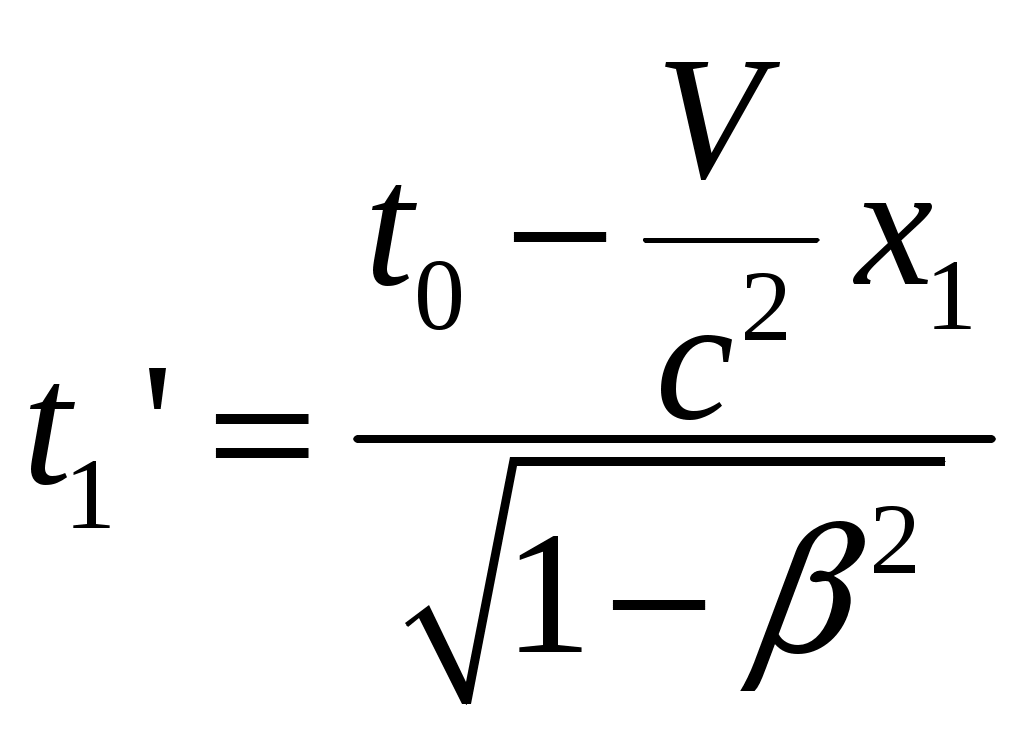 ;  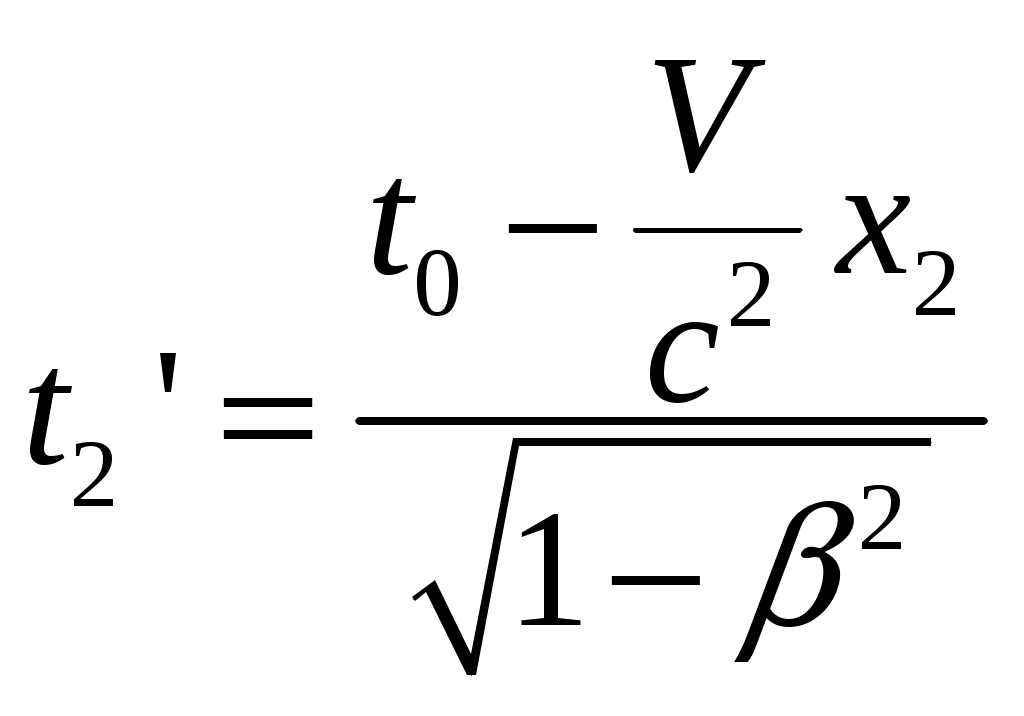Далее найдем разность моментов времени и координат в К’ - системе: (1)  (2)  Анализ выражений (1) и (2): 1) Если события в К - системе происходят одновременно ( ) и в одном и том же месте пространства, то есть  , то из (1) и (2) следует:  то есть эти события являются одновременными и происходят в одном и том же месте пространства и в К’ - системе (то есть в любой инерциальной системе отсчета). 2) Если события в К - системе происходят одновременно ( ), но пространственно разобщены, то есть  , то в системе К’ эти события остаются пространственно разобщенными, то есть и являются неодновременными, то есть  Обратим внимание: а) при   б) при   то есть в любой системе К' события оказываются неодновременными, причем в одних системах второе событие будет происходить позже первого (случай а), где  ); а в других системах второе событие будет происходить раньше первого (случай б), где  ).Нужно иметь в виду, что полученный результат относится лишь к событиям, причинно не связанными друг с другом (очевидно, что события происходят одновременно в разных точках пространства, не могут оказывать воздействия друг на друга). Иначе обстоит дело, если между событиями имеется причинная связь. В этом случае события - причина во всех системах отсчета предшествует событию - следственно. Рождение элементарной частицы во всех системах отсчета происходит раньше ее распада. Ни в одной из систем «сны не рождаются раньше отца». 2. Длина тел в разных системах отсчета. Сравним длину стрежня в инерциальных системах отсчета К и K’ (смотрите рисунок). 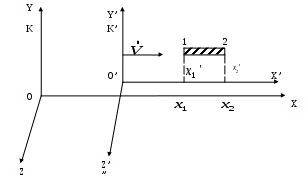 Предположим, что стержень покоится в K’ - системе. Разность координат  и  дает длину  стержня в K’ - системе: В системе К дело обстоит сложнее. Относительно этой К - системы стержень движется со скоростью (где - скорость, с которой К’ - система движется относительно К - системы). Так как стержень движется, нужно произвести одновременный отсчет координат его концов и в некоторый момент времени t в системе К*.Разность координат и даст длину стержня  в К - системе: Для сопоставления длин и  надо в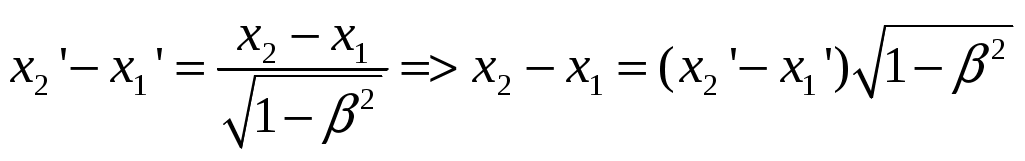зять формулу перехода  преобразований Лоренца, которая связывает координаты  ,  и время t системы К: ;  Отсюда:  ______________________________________________________________________________________* Необходимо измерить координаты его концов и в системе К в один и тот же момент времени (то есть t - это время системы К, а не К’).Заменим разности координат длинами стержня, получаем формулу:  Вывод: длина движущегося стержня оказывается меньше той, которой обладает стержень в состоянии покоя ( - длина стержня в состоянии покоя).Аналогичный эффект наблюдается для тел любой формы: в направлении движения линейные размеры тела сокращаются тем больше, чем больше скорость движения. Это явление называется лоренцовым (или фицджеральдовым) сокращением. Поперечные размеры тела не изменяются. В результате, например, шар принимает форму эллипсоида, сплющенного в направлении движения. Однако из-за искажения зрительного восприятия этот эллипсоид будет восприниматься в виде шара. 3. Длительность событий* в разных системах отсчета. (Промежуток времени между двумя событиями в разных системах отсчета). Определение: Длительностью (промежутком времени) между двумя событиями называется время, произошедшее между этими событиями, измеренное часами, расположенными в данной системе отсчета. Пусть в точке А, неподвижной относительно системы K’, в момент времени  и  произошли два события. Например, это могут быть: 1) два последовательных удара метронома, отбивающего каждую секунду; 2) рождение элементарной частицы и ее последующий распад;3) качающийся маятник дважды прошел положение равновесия.  Промежуток времени между этими событиями в К’ - системе равен:  Определение: Время, измеряемое в системе отсчета, где точка А неподвижна , называется собственным временем. Собственное время отсчитывается по часам, движущимся вместе с системой отсчета (В нашем случае собственное время отсчитывает часы, движущиеся вместе с К’ - системой отсчета). ______________________________________________________________________________________ * Событиями называют любые явления, происходящие с телами. Далее найдем промежуток времени 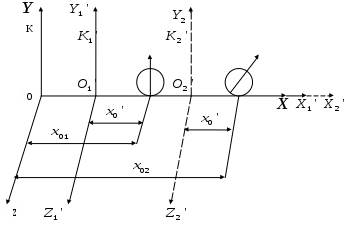 между этими событиями в системе К, относительно которой система К’ движется со скоростью  . Для этого определим в системе К момент времени  и  , соответствующие моментам и и образуем их разность: где и - время наступления событий по часам системы К. Заметим, что относительно системы К события «движутся», то есть происходят (свершаются) в разных точках пространства с координатами  и  (см. рис.), причем  . Для сопоставления времен  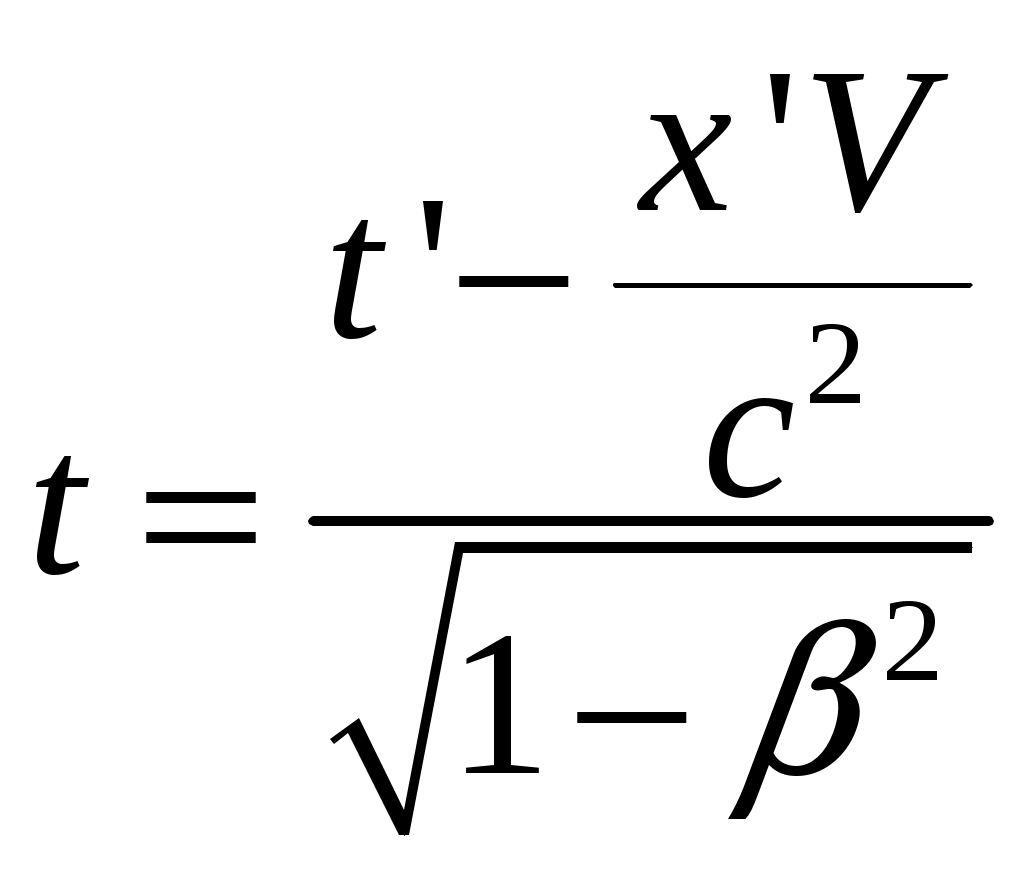и  обратимся к преобразованиям Лоренца, а именно к формуле:(  )  В нашем случае, подставляя в эту формулу моменты времени 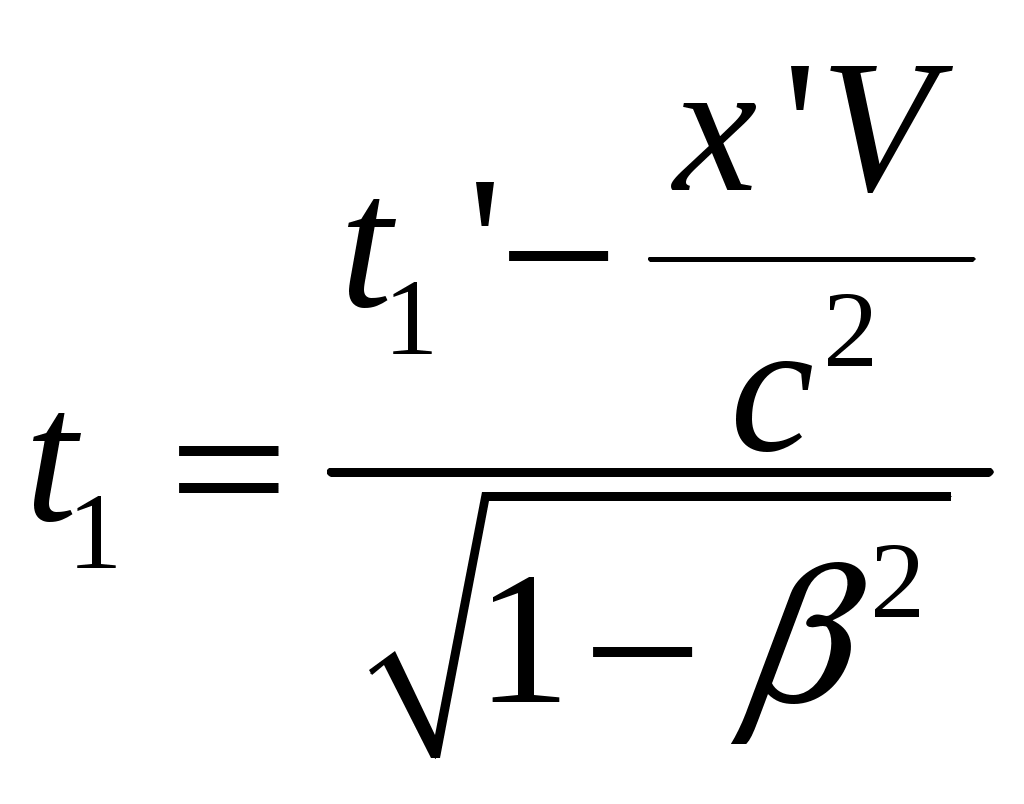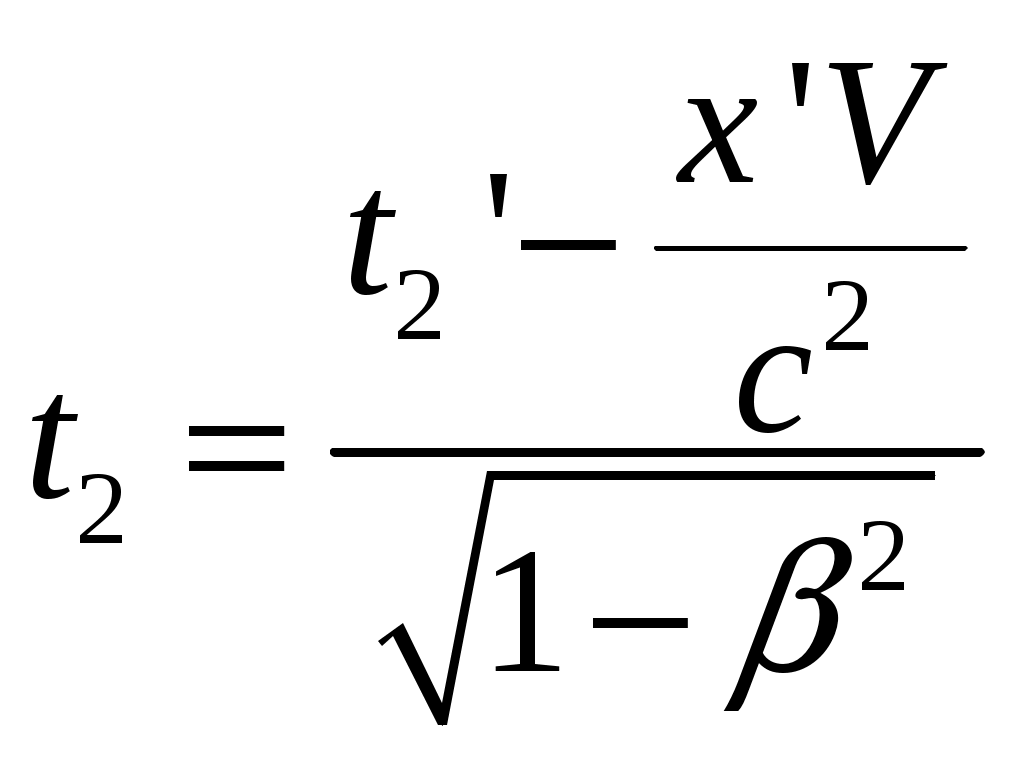и и координату  , получим: ;  .Отсюда 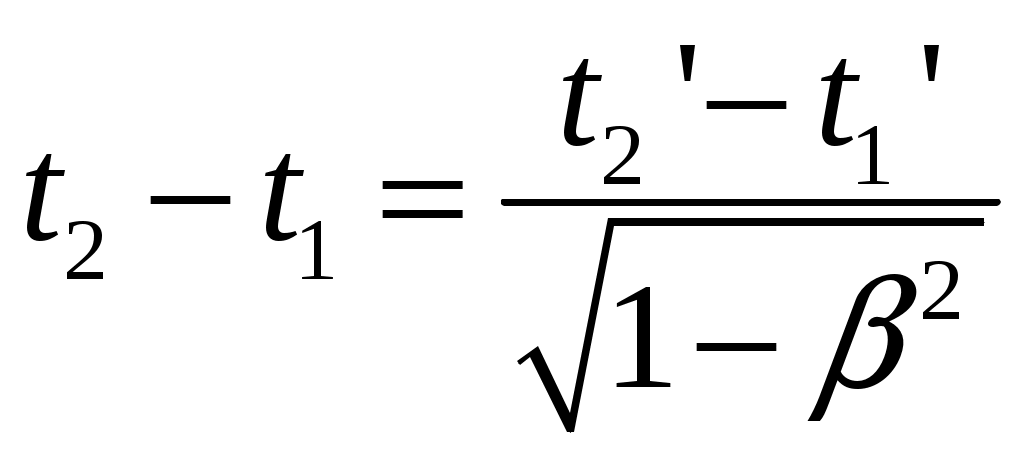 Так как  ;  , то получаем (1)Анализ формулы (1): 1. Промежуток времени, измеренный по часам системы, относительно которых события движутся (это промежуток времени ), больше, чем промежуток времени, измеренный по часам системы, в которой события происходят в одной и той же точке (это промежуток времени  ).Другими словами, промежуток времени между двумя событиями минимален в той инерциальной системе отсчета, относительно которой обо события совершаются в одной и той же точке (В нашем случае - это точка А, которая неподвижна относительно системы К’. Поэтому можно сказать и так: собственное время меньше времени , отсчитанного по часам, движущимся относительно точки А, где происходят два события). Так как  , то делаем вывод: временной интервал между событиями оказывается относительной величиной, а не абсолютной, как считалось ранее в механике Ньютона.2. Проанализируем эти события с точки зрения наблюдателя, «живущего» в системе К: - это промежуток времени между событиями, измеренный по его неподвижным часам; - промежуток времени между теми же событиями, измеренный по часам, движущимся относительно наблюдателя со скоростью .Поскольку из (1) следует, что  , то можно сказать, что движущиеся часы идут медленнее, чем покоящиеся часы. |